Похожие презентации:
Решение задач повышенной сложности. (Часть 1)
1.
РЕШЕНИЕ ЗАДАЧПОВЫШЕННОЙ СЛОЖНОСТИ
Часть 1
Рабчук Людмила Васильевна
доцент кафедры физики УГАТУ
доцент кафедры физики, математики и информатики ИРО РБ
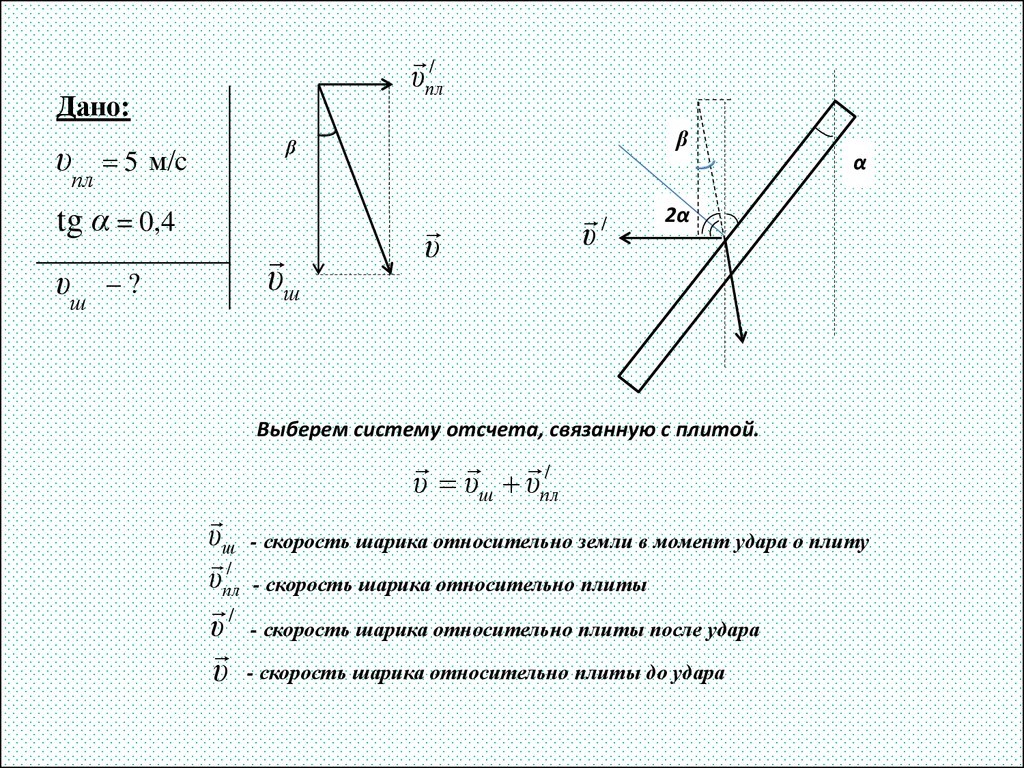
2. Задача 1
Массивнаяплита
движется
горизонтально со скоростью 5 м/с.
Шарик, летящий вертикально, после
упругого удара о плиту отскакивает
горизонтально в направлении движения
плиты (см рис.). Поверхность плиты
наклонена к вертикали под углом α,
тангенс которого равен 0,4. Найти
скорость шарика перед ударом.
(физтех, заочная олимпиада, 2016 г.)
α
3.
/υпл
Дано:
υпл 5 м/c
tg α = 0,4
υш
β
β
υш
–?
α
υ
/
υ
2α
Выберем систему отсчета, связанную с плитой.
υш
/
υпл
υ/
υ
/
υ υш υпл
- скорость шарика относительно земли в момент удара о плиту
- скорость шарика относительно плиты
- скорость шарика относительно плиты после удара
- скорость шарика относительно плиты до удара
4.
Задача 2Вертолет
летит
горизонтально
со
скоростью
υ 50 м/c ниже вершины
высокого обрыва на расстоянии l = 200 м
от него, двигаясь параллельно обрыву (см.
рисунок, вид сверху). В некоторый момент
пилот вертолета производит одиночный
выстрел из пушки. Через какое время
после выстрела пилот услышит эхо?
Скорость звука в воздухе с = 340 м/с.
(Всероссийская аэрокосмическая олимпиада, 2011 г.)
υ
l
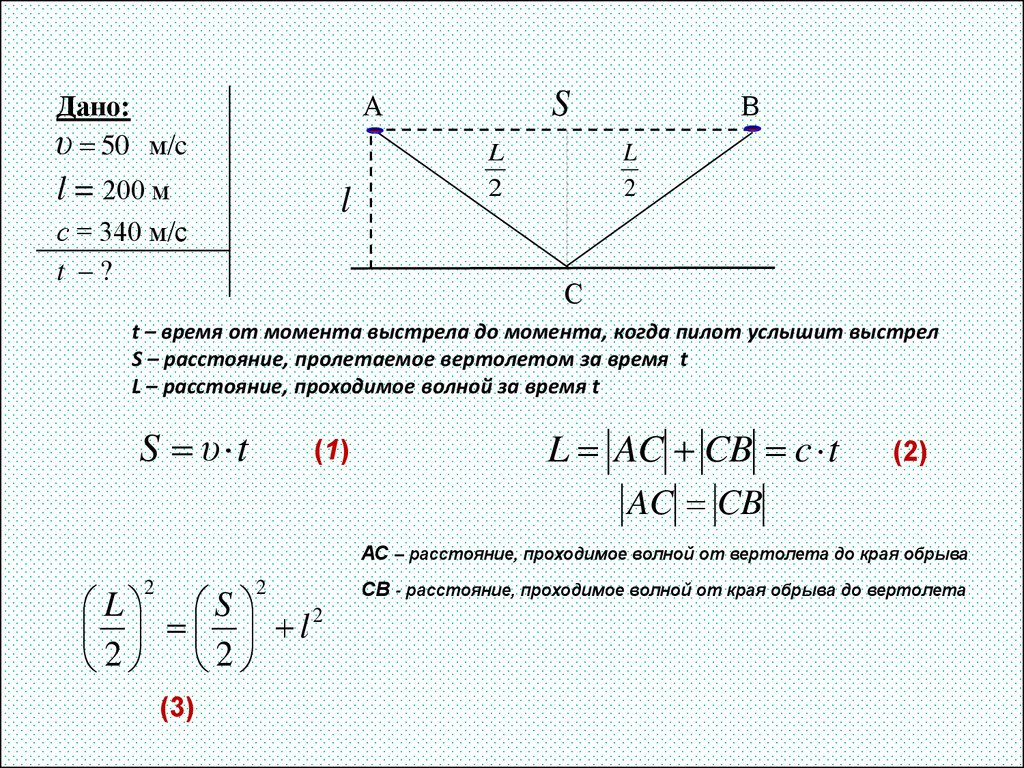
5. Задача 2
SА
Дано:
υ 50 м/c
l = 200 м
l
с = 340 м/с
t –?
L
2
В
L
2
С
t – время от момента выстрела до момента, когда пилот услышит выстрел
S – расстояние, пролетаемое вертолетом за время t
L – расстояние, проходимое волной за время t
S υ t
(1)
L AC CB c t
(2)
AC CB
АС – расстояние, проходимое волной от вертолета до края обрыва
2
2
L S
2
l
2 2
(3)
СВ - расстояние, проходимое волной от края обрыва до вертолета
6.
S υ tS 2 4l 2 c t
υ 2 t 2 4l 2 c 2 t 2
υ2 t 2 4l 2 c t
t
2l
c2 υ2
Ответ:
2 200
340 2 50 2
t = 1,2 с
1,2с
7.
Задача 3Два мячика брошены одновременно из разных точек,
расположенных на одной вертикали: мячик,
расположенный выше, брошен вертикально вниз с
начальной скоростью
υ1 2 м/c, а мячик,
расположенный ниже, брошен вертикально верх с
начальной скоростью
υ2 7 м/c. Мячики
сталкиваются, пролетев до столкновения (не меняя
направления движения) одинаковые расстояния.
Определите расстояние между мячиками в момент
начала
движения.
Сопротивлением
воздуха
пренебречь.
(Всероссийская аэрокосмическая олимпиада, 2014 г.)
8. Задача 3
Дано:Мячик, брошенный вниз, до встречи со
вторым мячом пролетает
υ1 2
υ2
м/c
7 м/с
Н–?
Мячик, брошенный вверх, до встречи с
мячом, брошенным вниз, проходит
g t2
S1 υ1 t
2
g t2
S 2 υ2 t
2
g t2
g t2
υ1 t
υ2 t
2
2
По условию :
S1 S2 S
υ2 υ1 7 2
t
0,5с
g
10
g t2
10 0,52
Н 2S 2(υ1 t
) 2(2 0,5
) 4,5 м
2
2
Ответ:
Н = 4,5 м
9.
Задача 4В момент времени t = 0 с с поверхности земли и с
высоты h = 5 м одновременно бросили два шарика из
пластилина: первый вертикально вверх с начальной
скоростью
υ1 4 м/c, а второй горизонтально с
начальной скоростью υ2 10 м/c. Через какое время
шарики окажутся на одной высоте? Сопротивлением
воздуха пренебречь. Ускорение свободного падения
считать равным 10 м/с2.
(Всероссийская аэрокосмическая олимпиада, 2014 г.)
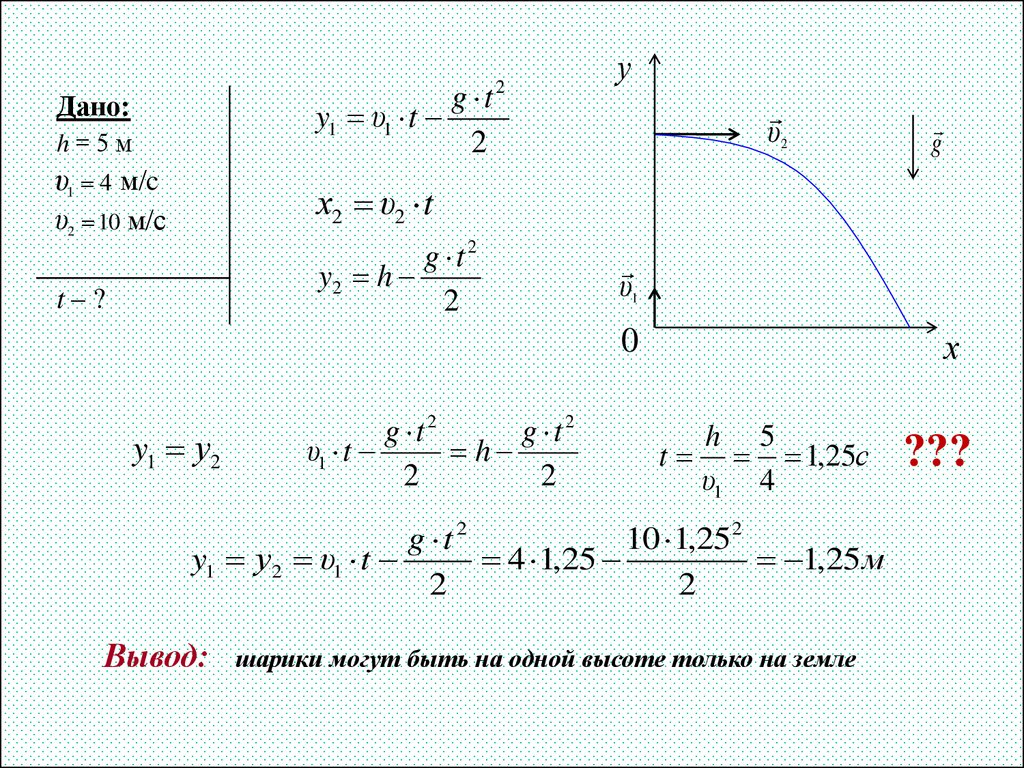
10. Задача 4
g ty1 υ1 t
2
Дано:
h=5м
υ1 4 м/c
2
у
υ2
g
х2 υ2 t
υ2 10 м/с
g t2
y2 h
2
t–?
υ1
0
y1 у2
g t2
g t2
υ1 t
h
2
2
х
t
h 5
1,25с
υ1 4
g t2
10 1,252
y1 у2 υ1 t
4 1,25
1,25 м
2
2
Вывод:
шарики могут быть на одной высоте только на земле
???
11.
g t12y1 0 υ1 t1
2
g t22
y2 0 h
2
t1
t2
2υ1 2 4
0,8с
g
10
2h
g
2 5
1с
10
Первым на земле окажется шарик, брошенный вертикально,
вторым – шарик, брошенный горизонтально.
Через 1 с оба
шарика будут уметь координату по оси OY, равную нулю.
Ответ:
t=1c
12.
Задача 5Колобок, спасаясь от гибели, катился в n = 2 раза
быстрее, чем бежал за ним хромой волк, при этом
расстояние между ними увеличивалось со
скоростью υ 0,628 м/c. Бедный колобок каждую
секунду утыкался носом в землю. Ему повезло,
тропинка была не скользкая. Какого диаметра
колобок испекла бабушка?
(Всероссийская аэрокосмическая олимпиада, 2013 г.)
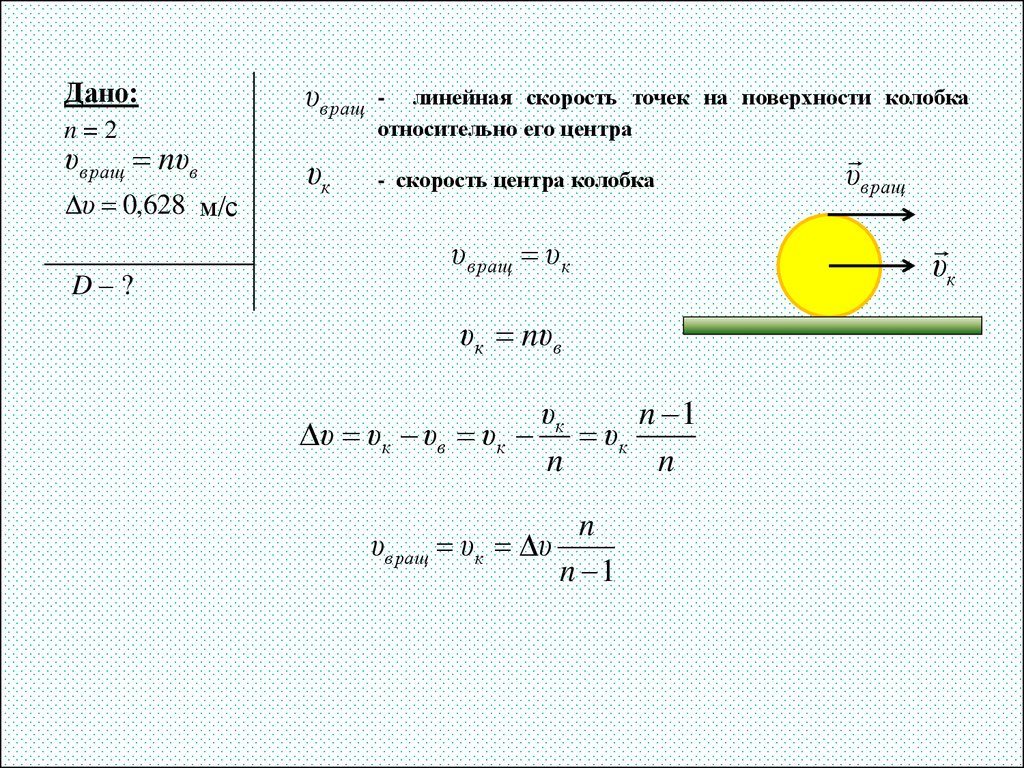
13. Задача 5
Дано:υв ращ
n=2
υвращ nυв
υ 0,628 м/с
D–?
υк
- линейная скорость точек на поверхности колобка
относительно его центра
- скорость центра колобка
υвращ υк
υк nυв
υк
n 1
υ υк υв υк υк
n
n
υв ращ υк υ
n
n 1
υв ращ
υк
14.
t 1cS υвращ t
S D
- путь, проходимый колобком
n
D υ
t
n 1
n
2
D υ
t 0,628
1 0,4 м 40см
(n 1)
(2 1)
Ответ:
D = 40 cм
15.
Задача 6Внутри вертикальной цилиндрической трубы с
внутренним радиусом R = 18 см находится маленький
шарик. Шарик толкнули от основания трубы по ее
внутренней
поверхности,
сообщив
начальную
скорость υ0 = 10 м/c, направленную под углом α = 30о
к горизонту. Сколько полных оборотов сделает шарик
внутри
трубы,
прежде
чем
опустится
на
первоначальный уровень? Трением, размерами
шарика и сопротивлением воздуха пренебречь.
(Всероссийская аэрокосмическая олимпиада, 2012 г.)
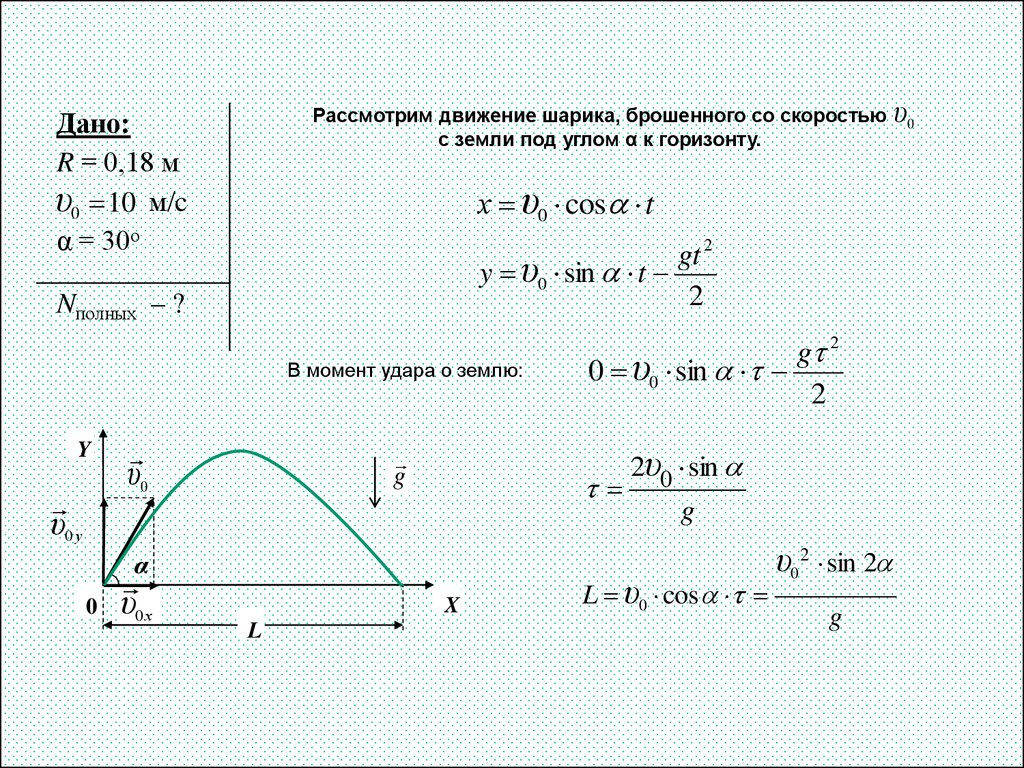
16. Задача 6
Рассмотрим движение шарика, брошенного со скоростьюс земли под углом α к горизонту.
Дано:
R = 0,18 м
υ0 10 м/c
α = 30о
х υ0 cos t
gt 2
y υ0 sin t
2
Nполных – ?
В момент удара о землю:
Y
υ0 у
υ0
g
α
0
υ0 х
X
L
g 2
0 υ0 sin
2
2υ0 sin
g
L υ0 cos
υ0 2 sin 2
g
υ0
17.
При движении шарика внутри трубы его траектория«закрученную» спираль с изменяющимся шагом.
L - расстояние,
представляет собой
пройденное шариком за время движения в горизонтальной плоскости
l - расстояние, проходимое в горизонтальной плоскости за каждый оборот шарик
N - число оборотов шарика внутри трубы за время опускания на
первоначальный уровень
l 2 R
υ02 sin 2
L
10 2 3
N
7,661
l
g 2 R
2 10 6,28 0,18
Ответ:
Nполных = 7
18.
Задача 7Планер описывает петлю Нестерова (окружность в
вертикальной плоскости). При этом в верхней точке
петли пилот прижимается к сиденью с силой, равной
силе тяжести. Чему равен коэффициент перегрузки
(отношение веса пилота к силе тяжести) в момент,
когда скорость планера направлена вертикально?
Силой сопротивления воздуха пренебречь.
(Всероссийская аэрокосмическая олимпиада, 2013 г.)
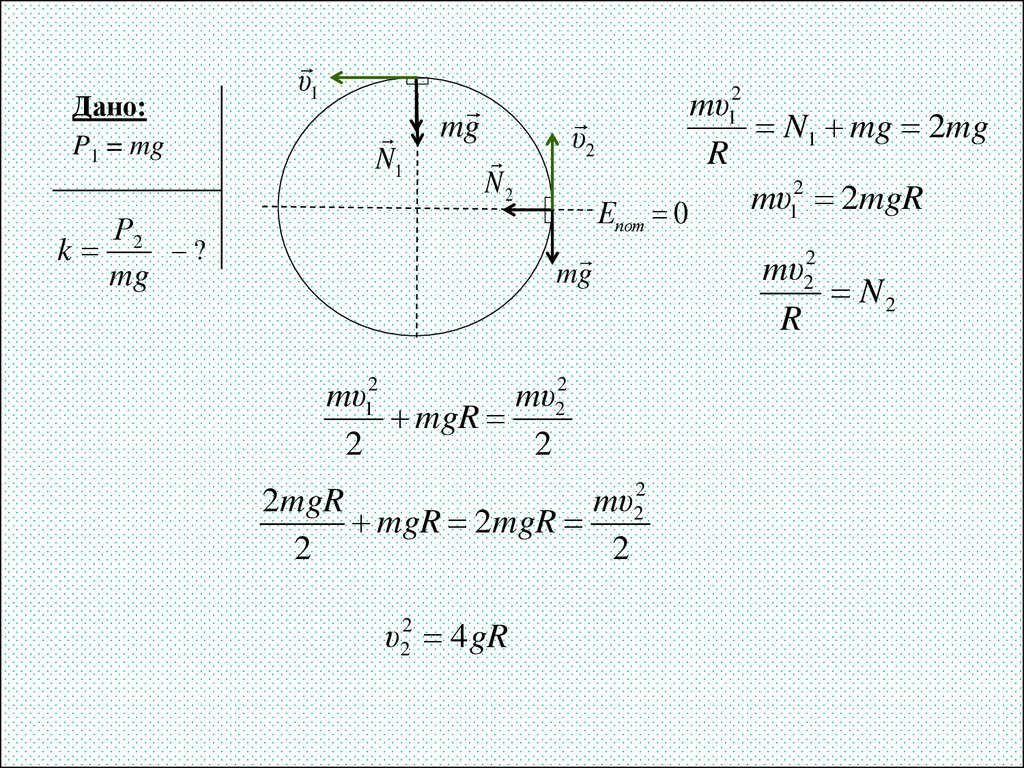
19. Задача 7
Дано:P1 = mg
υ1
N1
mg
υ2
N2
Р
k 2 –?
mg
Епот
mg
mυ12
mυ22
mgR
2
2
2mgR
mυ22
mgR 2mgR
2
2
υ22 4 gR
mυ12
N1 mg 2mg
R
2
mυ
1 2mgR
0
mυ22
N2
R
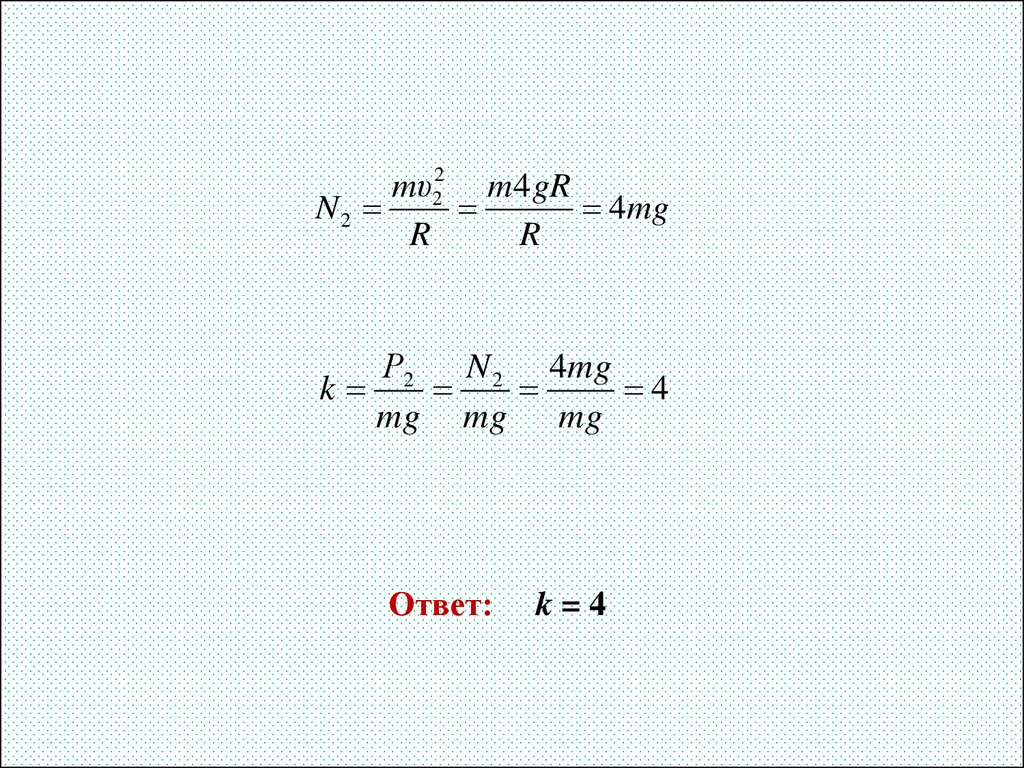
20.
mυ22 m4 gRN2
4mg
R
R
Р2
N 2 4mg
k
4
mg mg mg
Ответ:
k=4
21.
Задача 8Предположим, что планета Маленького принца имеет
среднюю плотность в n = 10 раз большую средней
плотности Земли. При каком минимальном радиусе
планеты Маленький принц сможет двигаться по ней
со скоростью υ 0,6 м/c, не рискуя превратиться в ее
искусственный спутник? Радиус Земли Rз= 6370 км.
(Всероссийская аэрокосмическая олимпиада, 2013 г.)
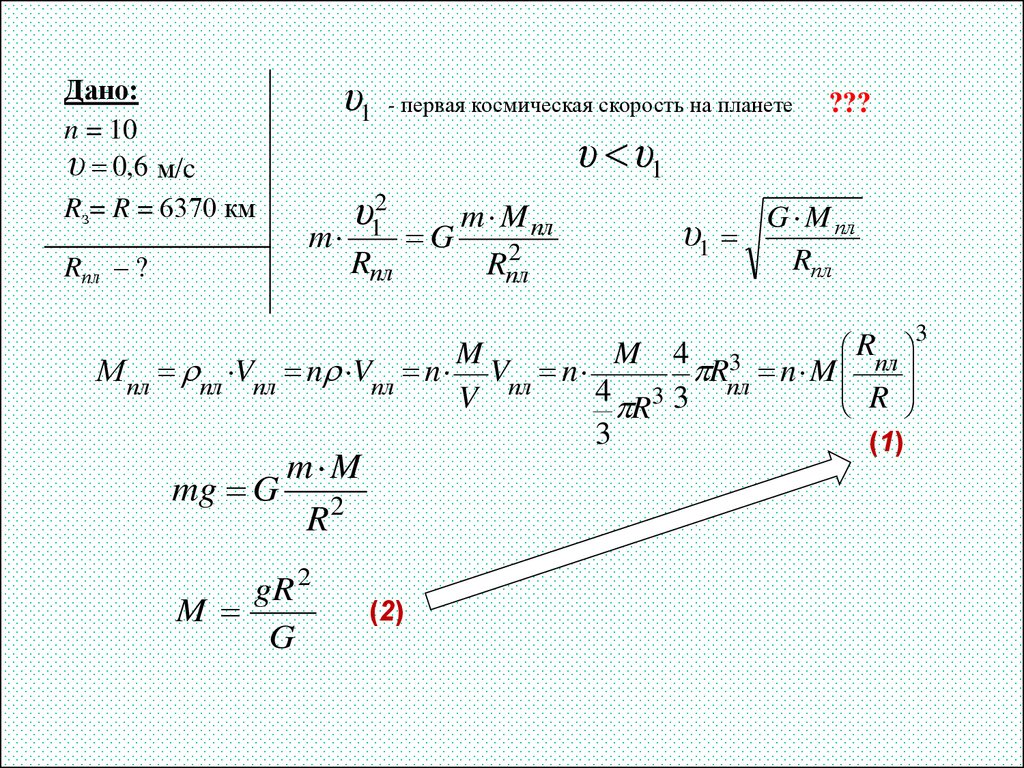
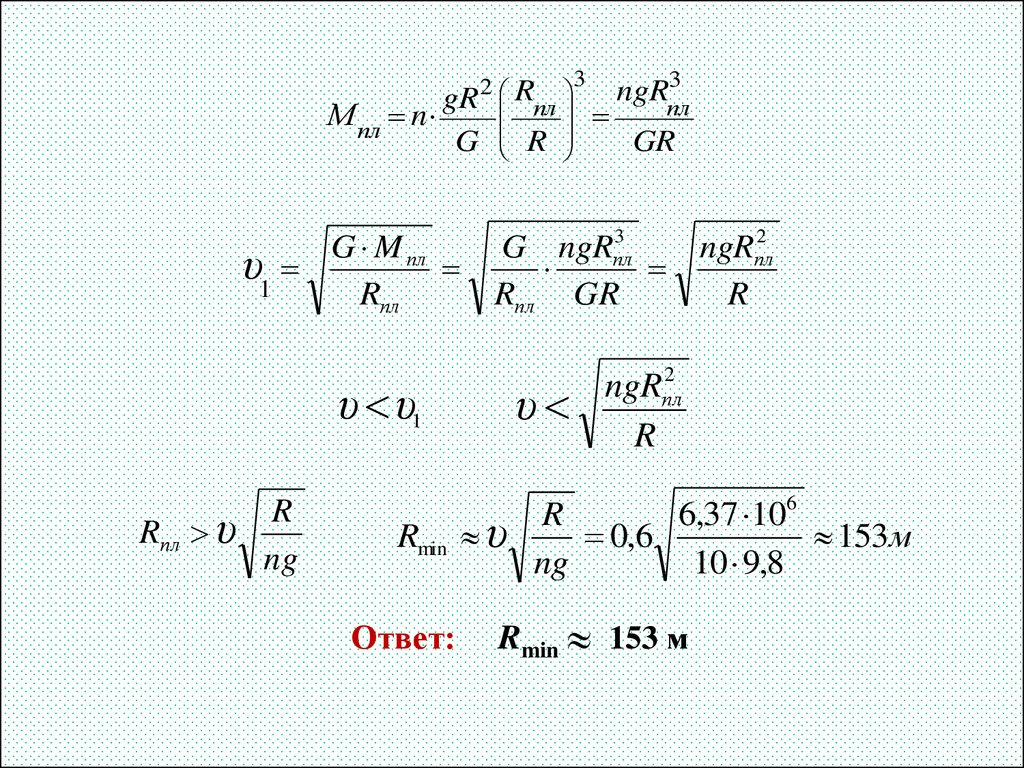
22. Задача 8
Дано:n = 10
υ 0,6 м/c
Rз= R = 6370 км
Rпл – ?
υ1
m
- первая космическая скорость на планете
υ12
Rпл
???
υ υ1
m M пл
G
2
Rпл
υ1
G M пл
Rпл
R
M
M 4 3
М пл пл Vпл n Vпл n Vпл n
Rпл n M пл
4 33
R
V
R
mg G
3
m M
R2
gR 2
M
G
(2)
(1)
3
23.
33
gR 2 Rпл ngRпл
М пл n
G R
GR
υ1 G M пл
Rпл
3
ngRпл2
G ngRпл
Rпл GR
R
υ
υ υ1
Rпл υ
R
ng
Rmin υ
Ответ:
ngRпл2
R
R
6,37 106
0,6
153м
ng
10 9,8
Rmin 153 м
24.
Задача 9Тело находится на поверхности Земли на широте
φ = 60о. Во сколько раз вес тела в данном месте
Земли отличается от веса этого же тела,
находящегося на полюсе? Радиус Земли Rз= 6400
км.
(Всероссийская аэрокосмическая олимпиада, 2013 г.)
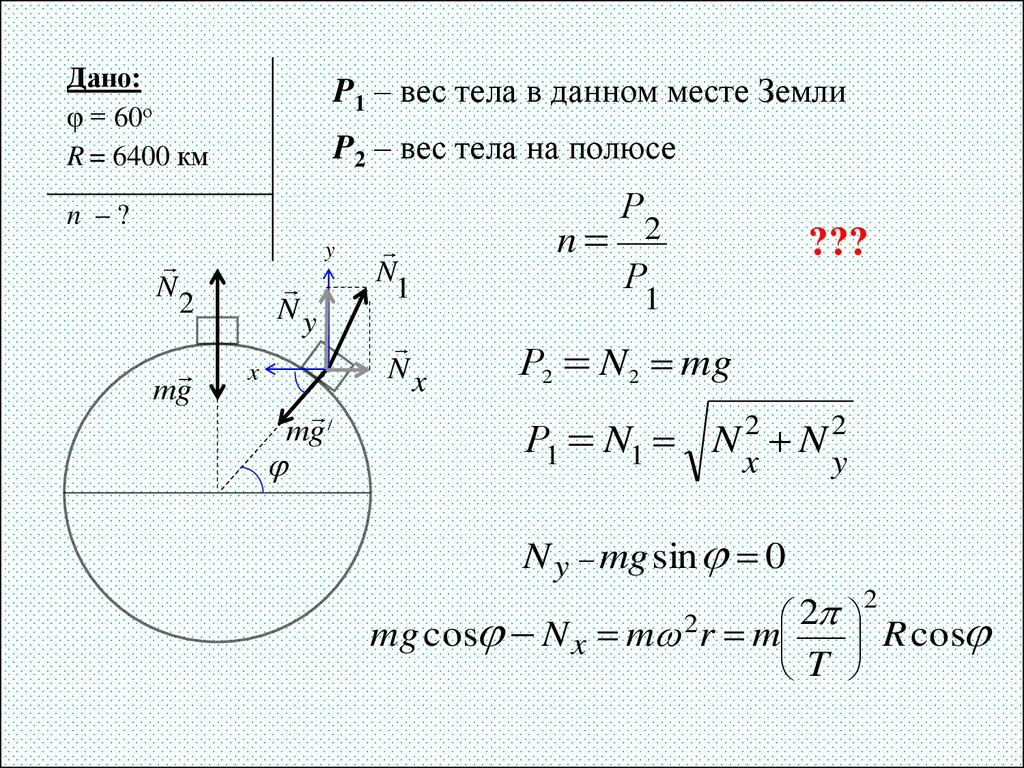
25. Задача 9
Дано:φ = 60о
R = 6400 км
P1 – вес тела в данном месте Земли
P2 – вес тела на полюсе
Р
n –?
N
y
Ny
2
mg
x
/
mg
N
1
Nx
n 2
Р
???
1
Р2 N 2 mg
Р1 N1 N 2 N 2
x
y
N y mg sin 0
2
2
mg cos N x m r m
T
2
R cos
26.
2N x mg cos m
T
2
2
R cos m g cos
T
N y mg sin
R cos
2
2
4
Р1 m g cos
R cos mg sin 2
2
T
2
2
2
4
Р1 m g cos
R cos g sin 2
2
T
2
27.
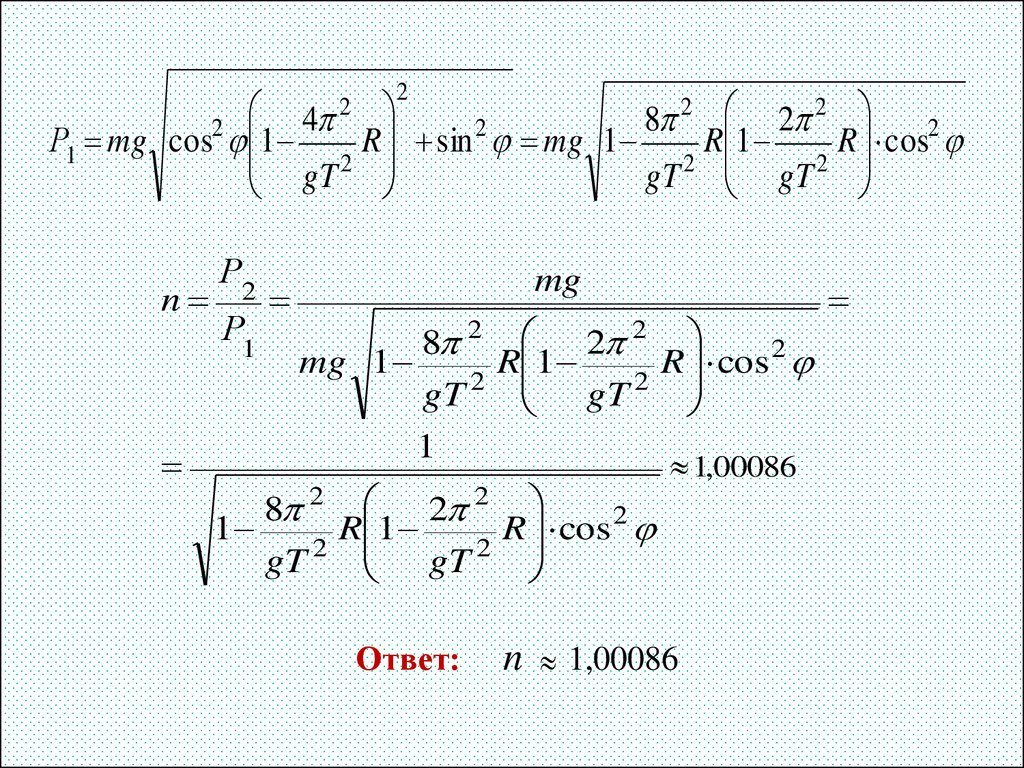
22
2
4
8
2
2
Р1 mg cos 1
R sin mg 1
R 1
R cos2
2
2
gT 2
gT
gT
2
2
n
Р2
Р1
mg
8 2 2 2
2
mg 1
R
1
R
cos
2
2
gT
gT
1
8 2 2 2
2
1
R
1
R
cos
2
2
gT
gT
Ответ:
1,00086
n 1,00086
28.
Задача 10Поезд массы М = 500 т шел равномерно по
горизонтальному пути. От поезда отцепился
последний вагон массы m = 20 т. В момент, когда
вагон остановился, расстояние между ним и
поездом было S = 500 м. Какой путь S1 прошел до
остановки вагон? Сопротивление движению
пропорционально массе и не зависит от скорости
поезда.
(Всероссийская аэрокосмическая олимпиада)
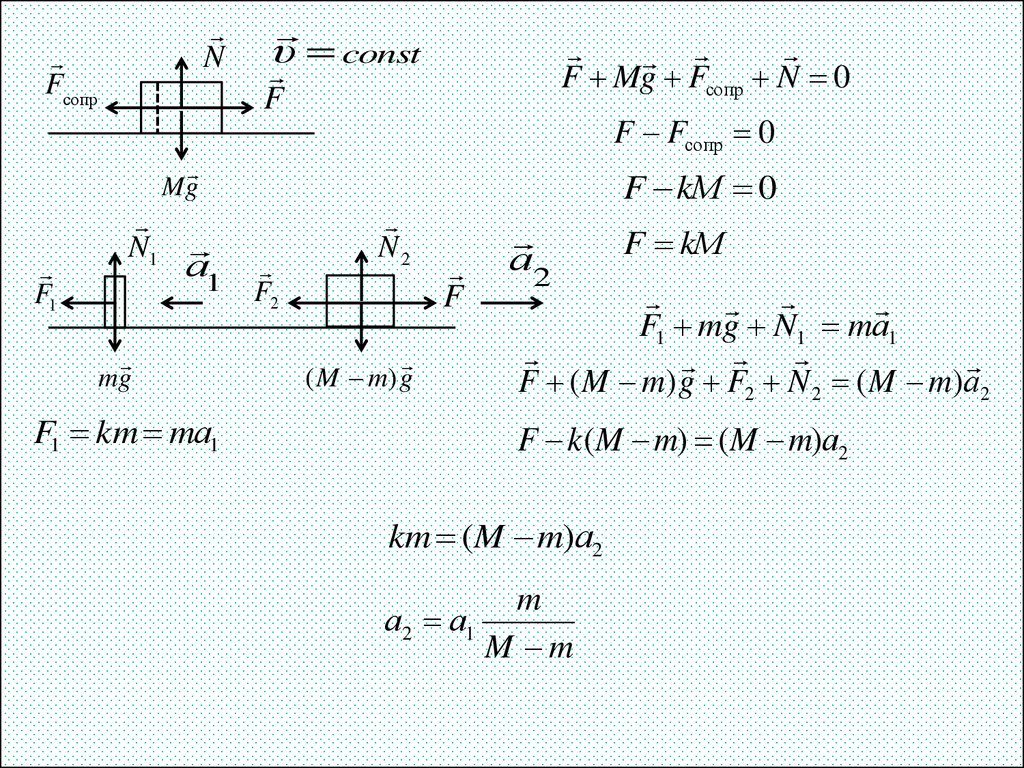
29. Задача 10
NFсопр
υ const
F Mg Fсопр N 0
F
F Fсопр 0
Mg
F1
N1
а1
mg
F2
N2
F kМ 0
F
( M m) g
F1 km mа1
а2
F kМ
F1 mg N1 mа1
F ( M m) g F2 N 2 ( M m)а2
F k (M m) (M m)а2
km (M m)а2
а2 а1
m
M m
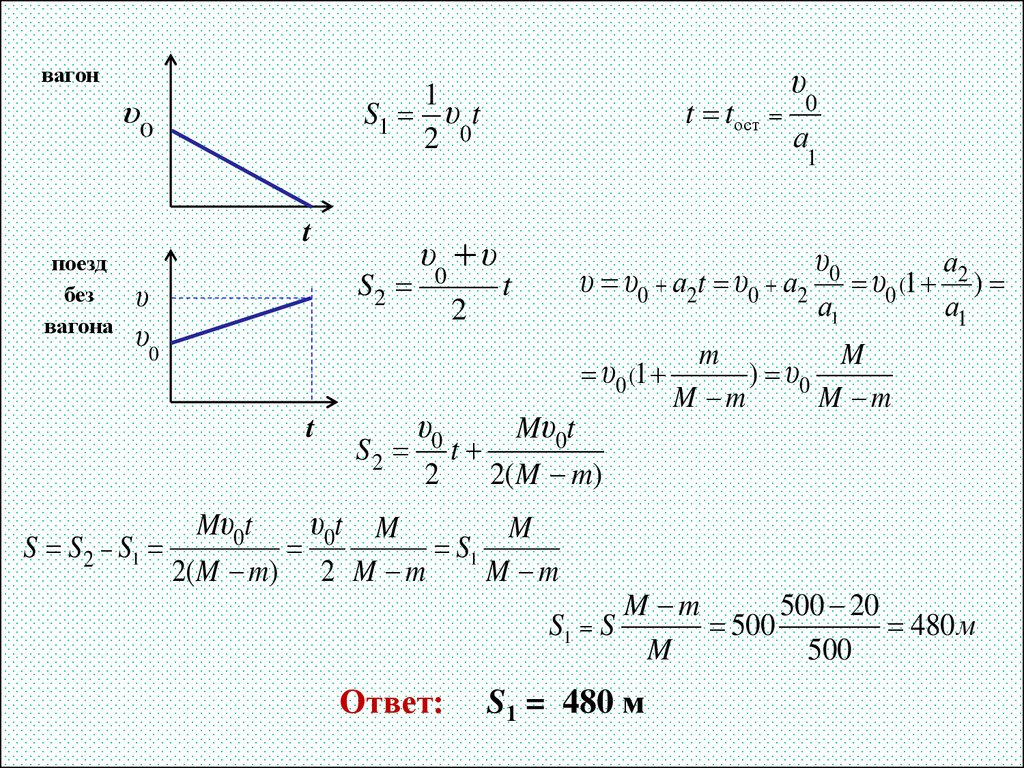
30.
вагон1
S1 υ t
2 0
υ0
t
поезд
без
вагона
S2
υ
υ0
t
S S 2 S1
t tост
а
1
υ0 υ
2
υ0
υ0
а2
υ υ0 а2t υ0 а2 υ0 (1 )
а1
а1
t
m
M
υ0 (1
) υ0
M m
M m
υ0
Mυ0t
S2 t
2
2( M m)
Mυ0t
υt M
M
0
S1
2( M m) 2 M m
M m
S1 S
Ответ:
M m
500 20
500
480 м
M
500
S1 = 480 м
31.
Задачи для самостоятельного решенияЗадача 1. Футболист ударил по мячу, сообщив ему
скорость υ0 под углом α к горизонту, и попал в
нижний угол ворот. Если бы футболист ударил по
мячу в том же месте поля и мяч полетел бы под тем же
углом к горизонту, но со скоростью, на 5% большей
скорости υ0 , то он попал бы в верхнюю штангу
ворот. Найти скорость υ0 , если высота ворот h = 2 м, а
угол α = 30о?
(Всероссийская аэрокосмическая олимпиада, 2013 г.)
Ответ:
υ0
21 м/c
32. Задачи для самостоятельного решения
Задача 2. Лиса Алиса и кот Базилио, обгладываякурочку, бросали кости в кувшин, в котором сидел
Буратино. Алиса и Базилио сидели на равных
расстояниях от кувшина и бросали кости с
одинаковой высоты, совпадающей с уровнем верхнего
края кувшина. Хитрая Алиса затрачивала на бросок
минимум энергии, а глуповатый Базилио тратил на
бросок в n = 2 раза больше энергии, чем Алиса, но оба
попадали в кувшин. Под каким углом к горизонту
бросал кости Базилио? Сопротивление воздуха не
учитывать.
(Всероссийская аэрокосмическая олимпиада, 2013 г.)
Ответ:
Б 15 или Б 75
33.
Задача 3. Орбитальная станция движется по круговойорбите радиусом R = 2 Rз, где Rз= 6370 км – радиус
Земли. Космонавт находится в открытом космосе.
Оцените силу, действующую на страховочный трос, к
которому пристегнут космонавт, полагая, что он
некоторое время находится на максимальном
удалении от Земли. Масса космонавта m =100 кг много
меньше массы станции, длина троса l = 100 м. Силой
тяжести троса и гравитационным взаимодействием
между станцией и космонавтом пренебречь.
(Всероссийская аэрокосмическая олимпиада, 2014 г.)
Ответ: Т 5,7 10 3 Н
34.
Задача 4. Шар радиусом R = 10 см лежит на днецилиндрического сосуда, заполненного раствором
некоторой соли в воде. Уровень раствора совпадает с
вершиной шара. Через некоторое время из-за
испарения воды в растворе оказалась погруженной
только половина объема шара. На сколько при этом
изменилась сила давления шара на дно сосуда?
Изменением объема воды, связанным с растворением
в ней соли, пренебречь. При испарении воды соль не
испаряется и не выпадает в осадок. Плотность чистой
воды ρ=103 кг/м3.
(Всероссийская аэрокосмическая олимпиада, 2015 г.)
Ответ: Р 20,5 Н
35.
Благодарю за внимание !rabtchuk_ludmila@mail.ru















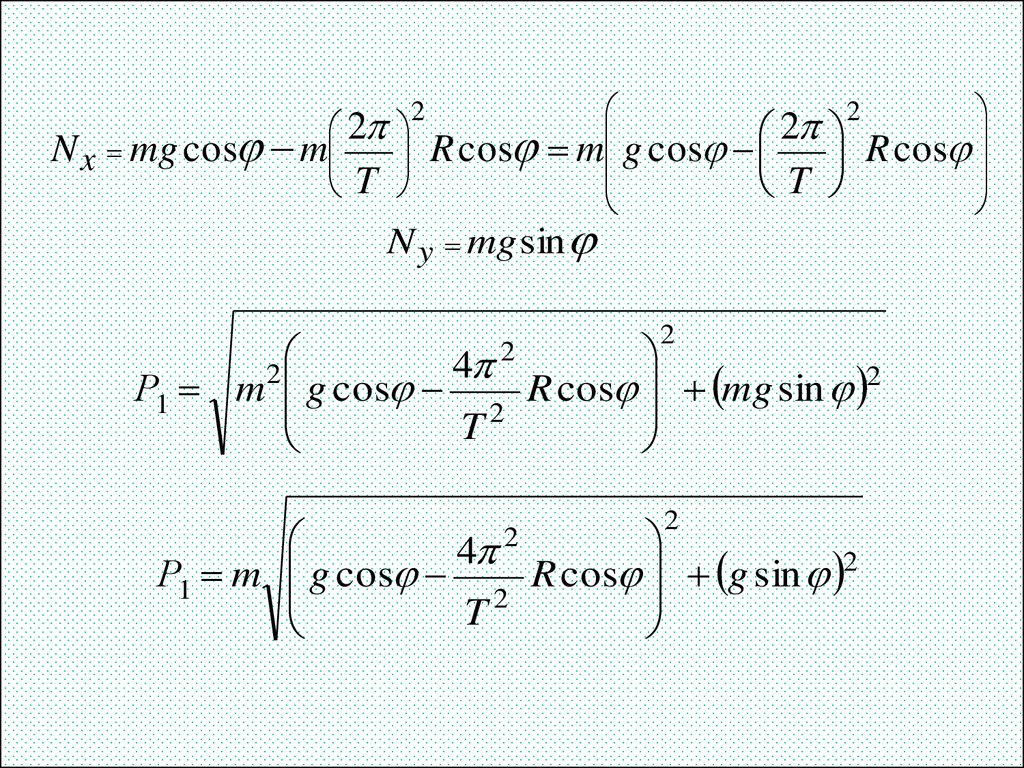






 Математика
Математика Физика
Физика








