Похожие презентации:
Практикум по решению задания №6 ЕГЭ по математике. Планиметрия
1.
Практикум по решению задания№6 ЕГЭ по математике
«ПЛАНИМЕТРИЯ»
(по материалам открытого
банка задач ЕГЭ
по математике
(профильный уровень)
2.
ПАРАЛЛЕЛОГРАММЗадание:
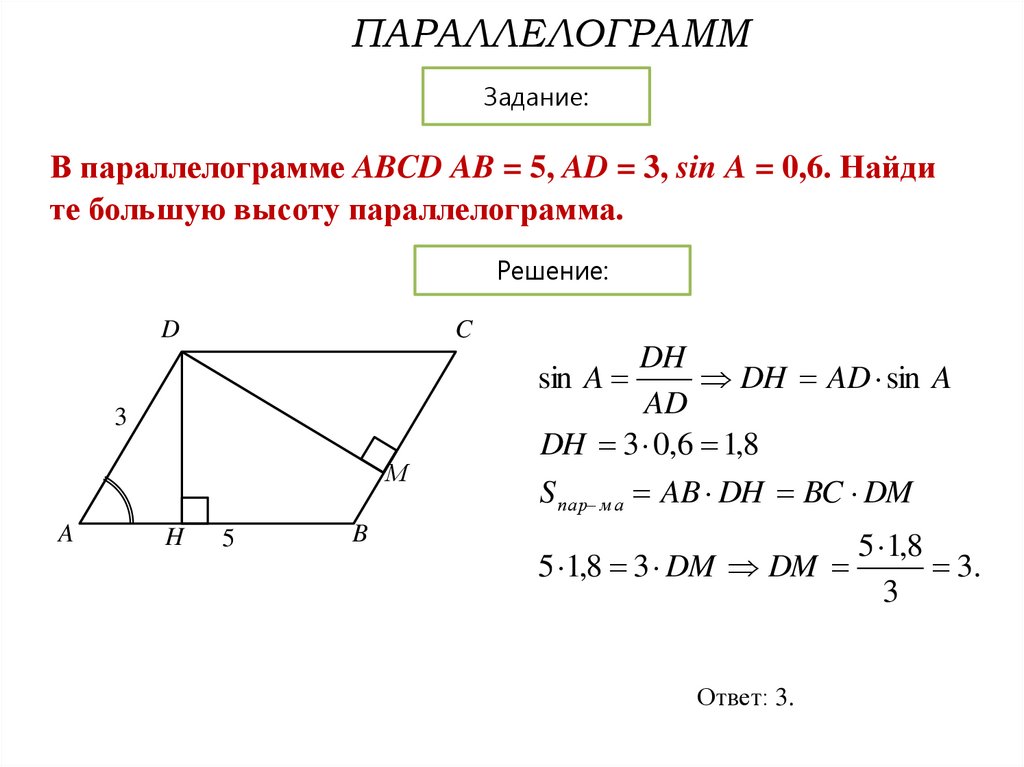
В параллелограмме ABCD AB = 5, AD = 3, sin A = 0,6. Найди
те большую высоту параллелограмма.
Решение:
C
D
3
М
A
H
5
B
DH
sin A
DH AD sin A
AD
DH 3 0,6 1,8
S пар м а AB DH BC DM
5 1,8
5 1,8 3 DM DM
3.
3
Ответ: 3.
3.
ПАРАЛЛЕЛОГРАММЗадание:
Стороны параллелограмма равны 22 и 44. Высота, опущенн
ая на первую из этих сторон, равна 33. Найдите высоту, опу
щенную на вторую сторону параллелограмма.
Решение:
D
C
44
S пар м а AB DH BC DM
33
22
33 22 44 DH
М
A
H
B
33 22
DH
16,5.
44
Ответ: 16,5.
4.
ПАРАЛЛЕЛОГРАММЗадание:
Биссектриса тупого угла параллелограмма делит противоположную
сторону в отношении 1 : 3, считая от вершины острого угла. Найдите
большую сторону параллелограмма, если его периметр равен 65.
Решение:
D
C
Пусть AМ х, тогда МB 3 х.
AMD CDM накрест лежащие
ADM CDM
х
х
A
(т.к. DM биссектриса )
3х
М
B
AMD ADM
ADM равнобедр. AD AM x;
AB 3 x x 4 x
Р 2 х 4 х 10 х
10 х 65
Ответ: 26.
х 6,5
большая сторона равна 4 6,5 26.
5.
ПАРАЛЛЕЛОГРАММЗадание:
Найдите угол между биссектрисами углов
параллелограмма, прилежащих к одной стороне. Ответ да
йте в градусах.
Решение:
AK , DM биссектрисы углов А и D,
K
D
C
у
ADM CDM y.
у
Т .к. сумма соседних углов паралле
O
х
лограмма ВАD ADС 180 ,
х
A
пусть ВАK DAK x,
M
B
то 2 х 2 у 180
х у 90
В AOD
х у АОD 180
Ответ: 90.
АOD 180 x y
АOD 180 90 90 , AOD прямоуг .
6.
ПАРАЛЛЕЛОГРАММЗадание:
Площадь параллелограмма ABCD равна 159. Точка E – середи
на стороны BC. Найдите площадь трапеции ADEB.
А
F
D
Решение:
B
E
Разобьем параллелограмм ABCD на равные
треугольники , как на рисунке их всего 4 ,
трапеция ADEB состоит из трех таких
треугольников , значит
3
S ABCD
4
3
159 119 ,25.
4
S ADEB
S ADEB
Ответ: 119,25.
C
7.
ПРЯМОУГОЛЬНИКЗадание:
Площадь прямоугольника равна 192. Найдите его большую
сторону, если она на 4 больше меньшей стороны.
Решение:
Пусть AB х , тогда АD х 4
х
S AB AD
192 x 4 x
х+4
x 2 4 x 192 0
x 12
x 16 не подходит по условию
AB 12
АD 12 4 16.
Ответ: 16.
8.
ПРЯМОУГОЛЬНИКЗадание:
Периметр прямоугольника равен 76, а площадь 192. Найдите
большую сторону прямоугольника.
Решение:
C
B
P 2 AB AD 2 х у
х
A
Пусть AB х, АD y, тогда
у
D
х у 38
х 38 у
x у 192
38 у у 192
у 2 38 у 192 0
у 32
у 6
х 32
х 6
или
у 6
у 32
76 2 х у х у 38
S AB AD x у 192
AB 6, АD 32.
9.
ПРЯМОУГОЛЬНИКЗадание:
Параллелограмм и прямоугольник имеют одинаковые стороны.
Найдите острый угол параллелограмма, если его площадь равна
половине площади прямоугольника. Ответ дайте в градусах.
Решение:
C
D
S ABCD AB AD sin A
S MNPQ MN MQ AB AD
A
т.к . АВ MN , MQ AD
B
Q
P
S ABCD AB AD sin A
1
sin A
S MNPQ
AB AD
2
A 30 .
M
N
Ответ: 30.
10.
РОМБЗадание:
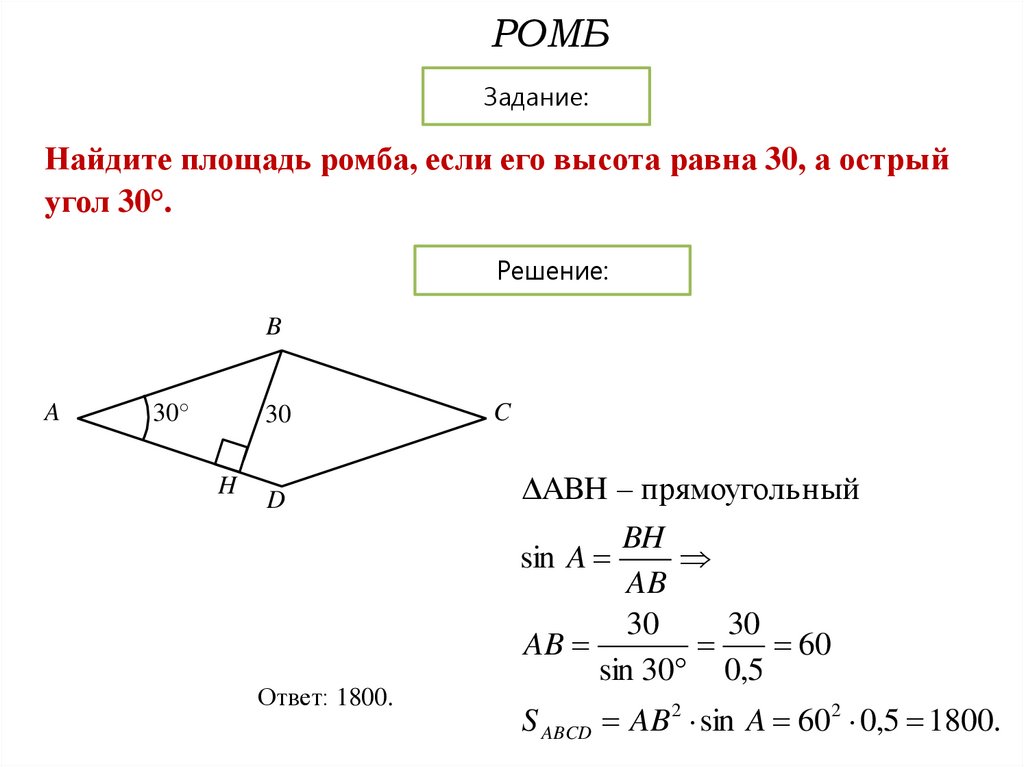
Найдите площадь ромба, если его высота равна 30, а острый
угол 30°.
Решение:
B
A
30°
30
H
D
C
ABH – прямоуголь ный
BH
AB
30
30
AB
60
sin 30 0,5
sin A
Ответ: 1800.
S ABCD AB 2 sin A 60 2 0,5 1800.
11.
РОМБЗадание:
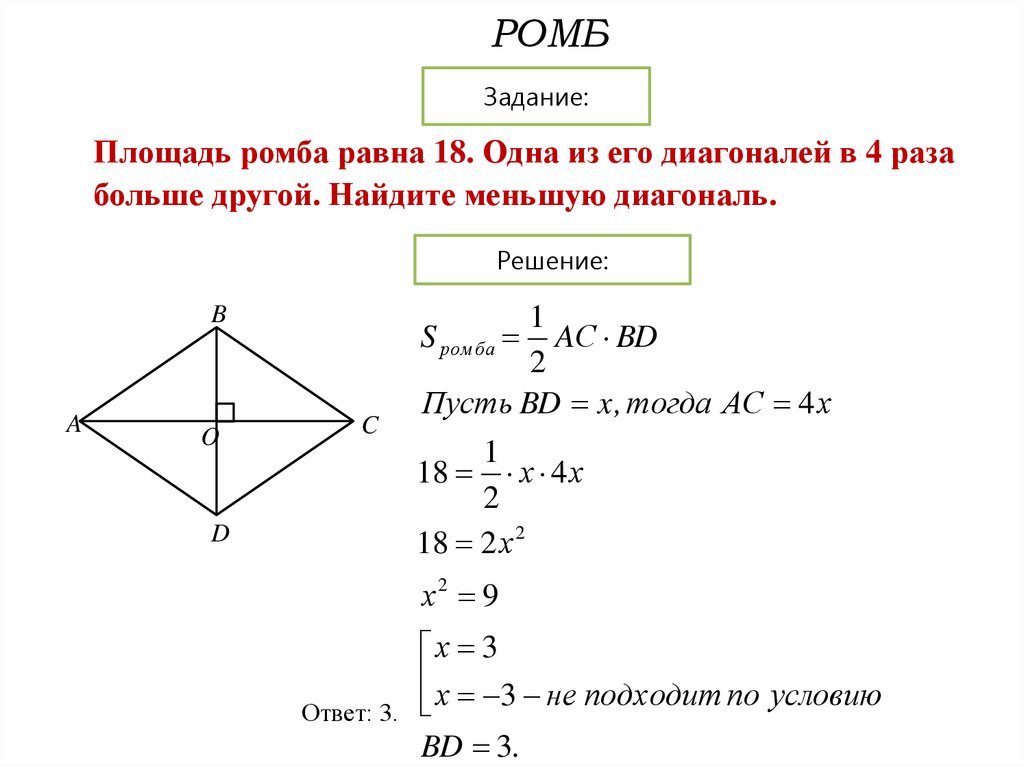
Площадь ромба равна 18. Одна из его диагоналей в 4 раза
больше другой. Найдите меньшую диагональ.
Решение:
B
A
O
C
1
S ром ба AС BD
2
Пусть BD x , тогда АС 4 х
1
х 4х
2
18 2 х 2
18
D
х2 9
Ответ: 3.
х 3
х 3 не подходит по условию
BD 3.
12.
РОМБЗадание:
Диагонали ромба относятся как 2 : 9. Периметр ромба равен 170.
Найдите высоту ромба.
Решение:
AOB – прямоуголь ный
B
A
O
C
HD
Пусть OB 2 x, AO 9 x, тогда
по т. Пифагора
АВ 2 АО 2 ОВ 2
АВ 2 9 х 2 х 85 х 2
2
85
85 , BD 2OB 2 85
2
85 9 85
AO 9
, AC 2 AO 9 85
2
2
1
1
S ром ба AC BD 2 85 9 85 765
2
2
S ром ба 765
S ром ба AD BH BH
18.
85
AD
2
OB 2
2
АВ 85 х, Р 4 АВ АВ
Р 170 85
4
4
2
85
85
85 х х
2
2
Ответ: 18.
13.
ТРАПЕЦИЯЗадание:
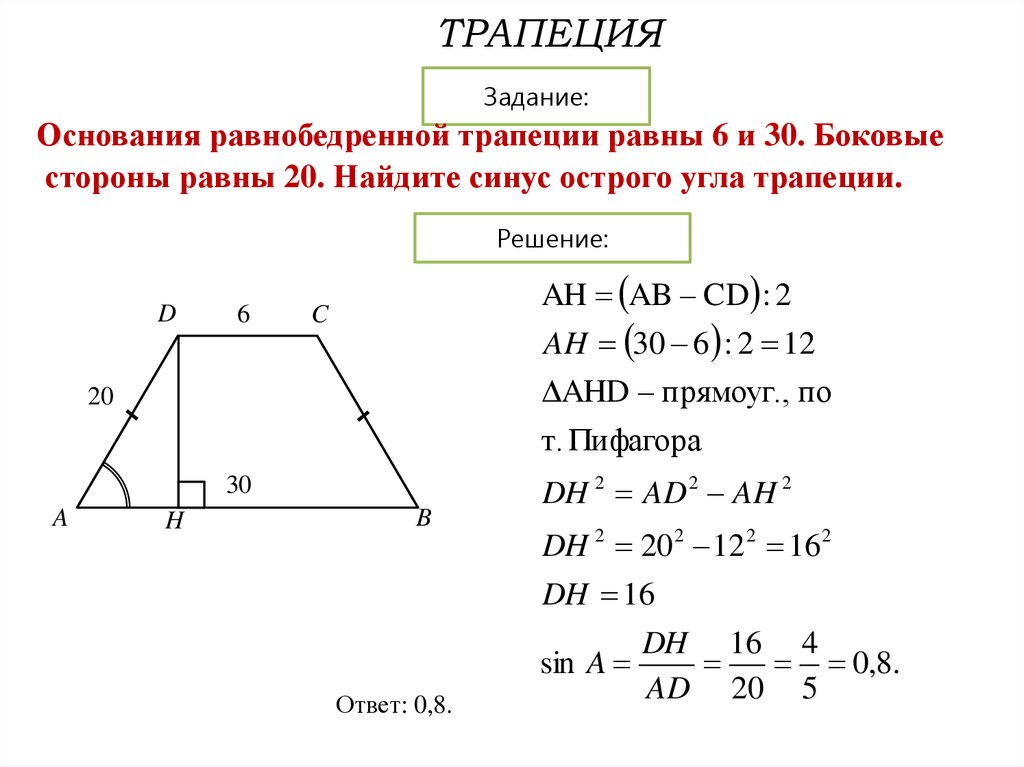
Основания равнобедренной трапеции равны 6 и 30. Боковые
стороны равны 20. Найдите синус острого угла трапеции.
Решение:
D
6
AH AB – CD : 2
C
AH 30 6 : 2 12
AHD – прямоуг., по
20
т. Пифагора
30
A
H
B
DH 2 AD 2 AH 2
DH 2 20 2 12 2 16 2
DH 16
Ответ: 0,8.
DH 16 4
sin A
0,8.
AD 20 5
14.
ТРАПЕЦИЯЗадание:
В равнобедренной трапеции диагонали перпендикулярны.
Высота трапеции равна 49. Найдите ее среднюю линию.
Решение:
F
D
C
O
49
45°
A
E
B
Если в равнобедренной трапеции
диагонали перпендикулярны, то
высота EF равна полусумме длин
оснований:
FO = DF, OE = AE
FE = FO + OE = DF + AE
FE = ½ AB + ½ CD
FE = ½ (AB + CD) – формула для
вычисления средней линии
трапеции
Ответ: 49.
15.
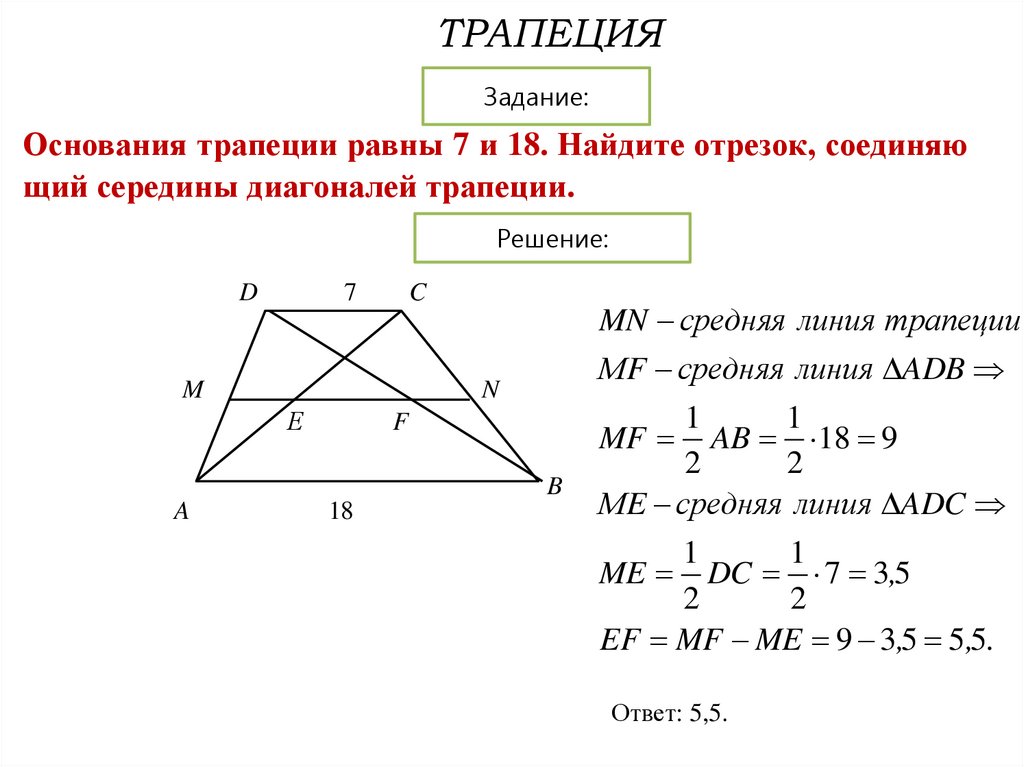
ТРАПЕЦИЯЗадание:
Основания трапеции равны 7 и 18. Найдите отрезок, соединяю
щий середины диагоналей трапеции.
Решение:
D
C
7
M
MN средняя линия трапеции
МF средняя линия ADB
N
Е
F
B
A
18
1
1
AB 18 9
2
2
МE средняя линия ADC
MF
1
1
ME DC 7 3,5
2
2
EF MF ME 9 3,5 5,5.
Ответ: 5,5.
16.
ТРАПЕЦИЯЗадание:
Основания равнобедренной трапеции равны 69 и 39, один из
углов равен 45°. Найдите высоту трапеции.
Решение:
D
39
AH AB – CD : 2
C
AH 69 39 : 2 15
AHD - прямоуголь ный
45°
A
и равнобедренный,
69
H
B
т.к. DAH 45
DH AH 15.
Ответ: 15.
17.
ТРАПЕЦИЯЗадание:
Основания прямоугольной трапеции равны 9 и 13. Ее площадь
равна 44. Найдите острый угол этой трапеции. Ответ дайте
в градусах.
Решение:
D
9
C
HB AB CD 13 9 4
AB CD
СH
2
2S
2 44
CH
4
AB CD 13 9
CBH - прямоуг. и равноб.
S
A
B
H
13
т т. СН ВН 4
СВН 45 .
Ответ: 45.
18.
ТЕСТ (проверь свои знания по теме…)Площадь параллелограмма равна 140, две его сторон
ы равны 10 и 35. Найдите большую высоту этого пара
ллелограмма.
1
2
1) 5
2) 14
3) 6
Точка пересечения биссектрис двух углов параллелограмма, приле
жащих к одной стороне, принадлежит противоположной стороне.
Меньшая сторона параллелограмма равна 5. Найдите его большую
сторону.
3
1) 10
2) 9
3) 28
Найдите периметр прямоугольника, если его площадь равна
270, а отношение соседних сторон равно 2 : 15.
4
1) 75
2) 49
3) 102
Периметр прямоугольника равен 26, а диагональ равна 12.
Найдите площадь этого прямоугольника.
1) 12,5
2) 12
3) 55
19.
56
Найдите высоту ромба, сторона которого равна 33 3
а острый угол равен 60°.
1) 49,5 2) 40,8 3) 45
,
Сторона ромба равна 38, острый угол равен 30°.
Найдите радиус вписанной окружности этого ромба.
1) 12 2) 15
3) 19
7
Основания равнобедренной трапеции равны 24 и 28.
Косинус острого угла трапеции равен 0,2. Найдите
боковую сторону.
1) 40 2) 20 3) 10
8
Найдите площадь прямоугольной трапеции, основания
которой равны 2 и 12, большая боковая сторона составляет
с основанием угол 45°.
1) 25
2) 70 3) 60
20.
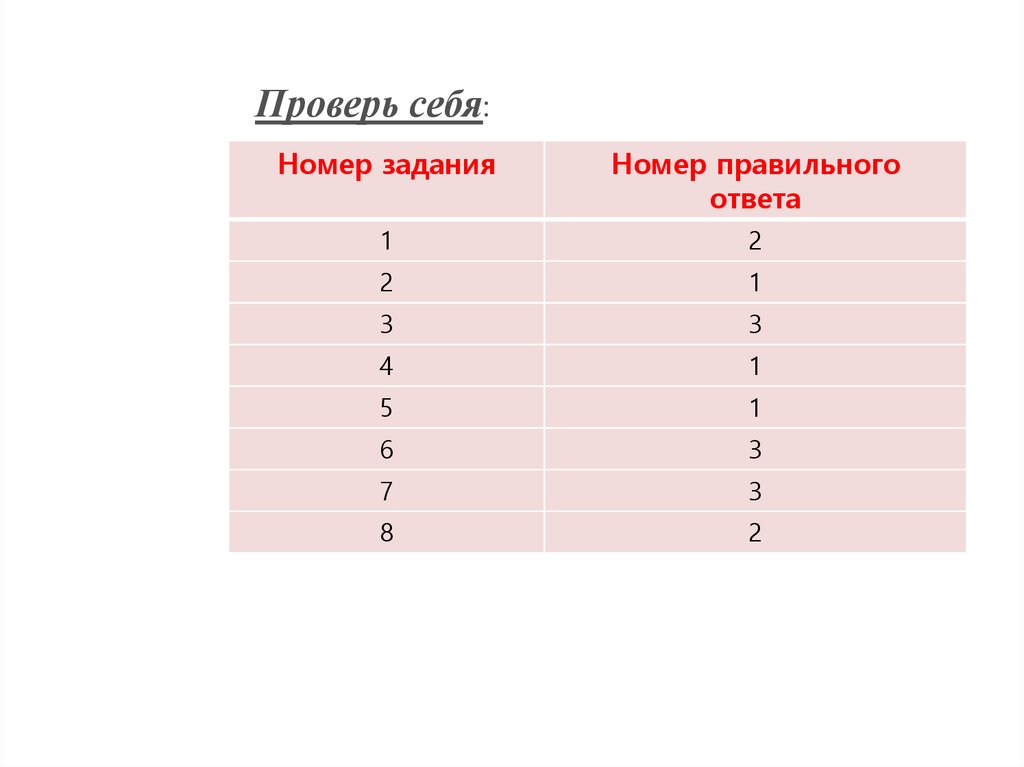
Проверь себя:Номер задания
Номер правильного
ответа
1
2
2
1
3
3
4
1
5
1
6
3
7
3
8
2















 Математика
Математика








