Похожие презентации:
Медианы, биссектрисы и высота треугольника
1.
2. Замечание!!!
Определение перпендикуляра кпрямой (описательное) изучаем
из пункта 16;
теорему о проведении
перпендикуляра к прямой также
изучаем по пункту 16 с
доказательством
3. Замечание!!!
На след слайде изучим какможно построить перпендикуляр
из точки к прямой!!!
4.
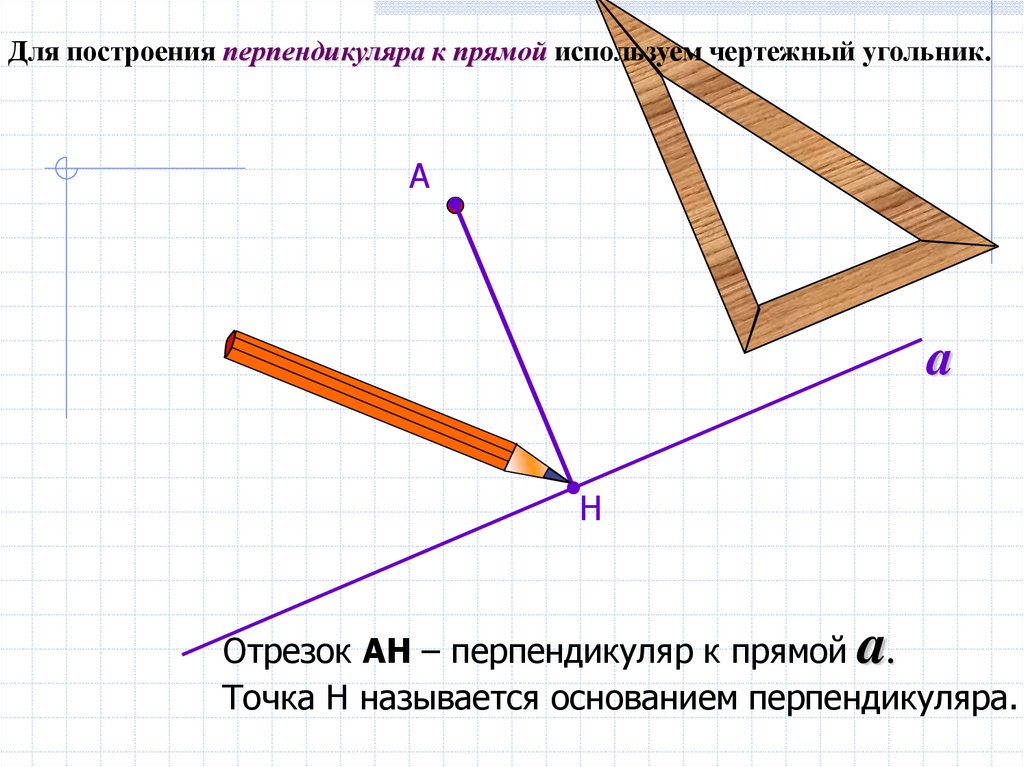
Для построения перпендикуляра к прямой используем чертежный угольник.А
a
Н
a
Отрезок АН – перпендикуляр к прямой .
Точка Н называется основанием перпендикуляра.
5. Замечание!!!
На след слайде подводиммышку на слова медиана,
высота, биссектриса и изучаем
эти понятия
6.
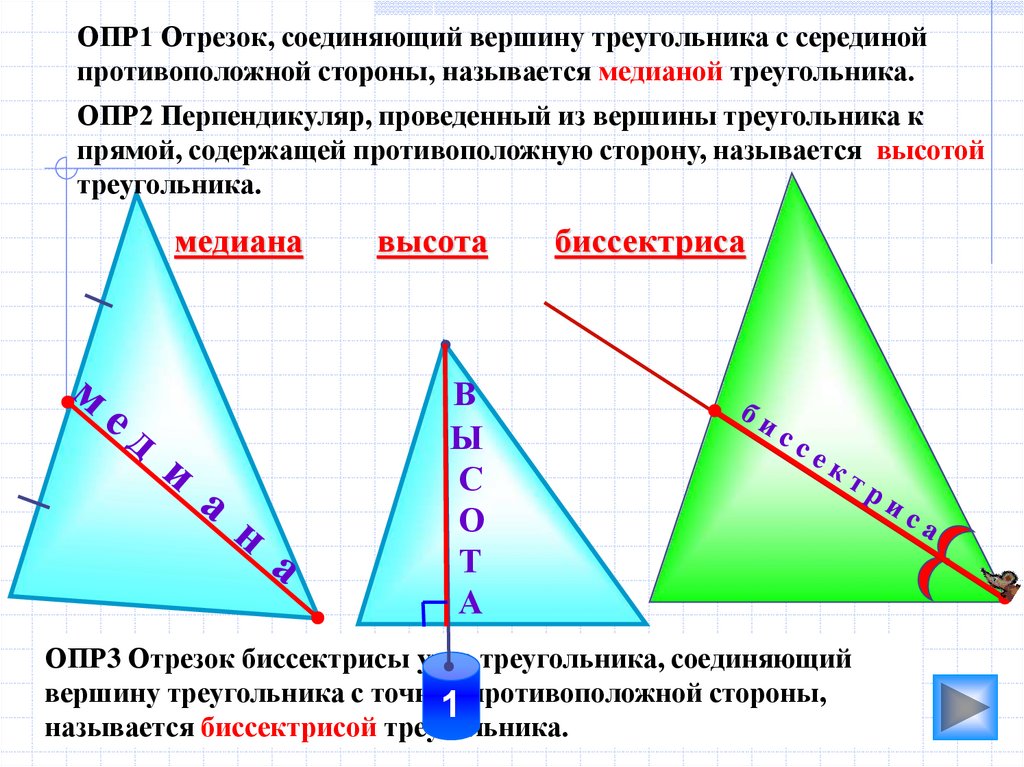
ОПР1 Отрезок, соединяющий вершину треугольника с серединойпротивоположной стороны, называется медианой треугольника.
ОПР2 Перпендикуляр, проведенный из вершины треугольника к
прямой, содержащей противоположную сторону, называется высотой
треугольника.
медиана
высота
биссектриса
В
Ы
С
О
Т
А
ОПР3 Отрезок биссектрисы угла треугольника, соединяющий
вершину треугольника с точкой противоположной стороны,
1
называется биссектрисой треугольника.
7. Замечание!!!
На след слайде еще раз напримере устной задачи
отрабатываем понятия медиана,
высота, биссектриса
8.
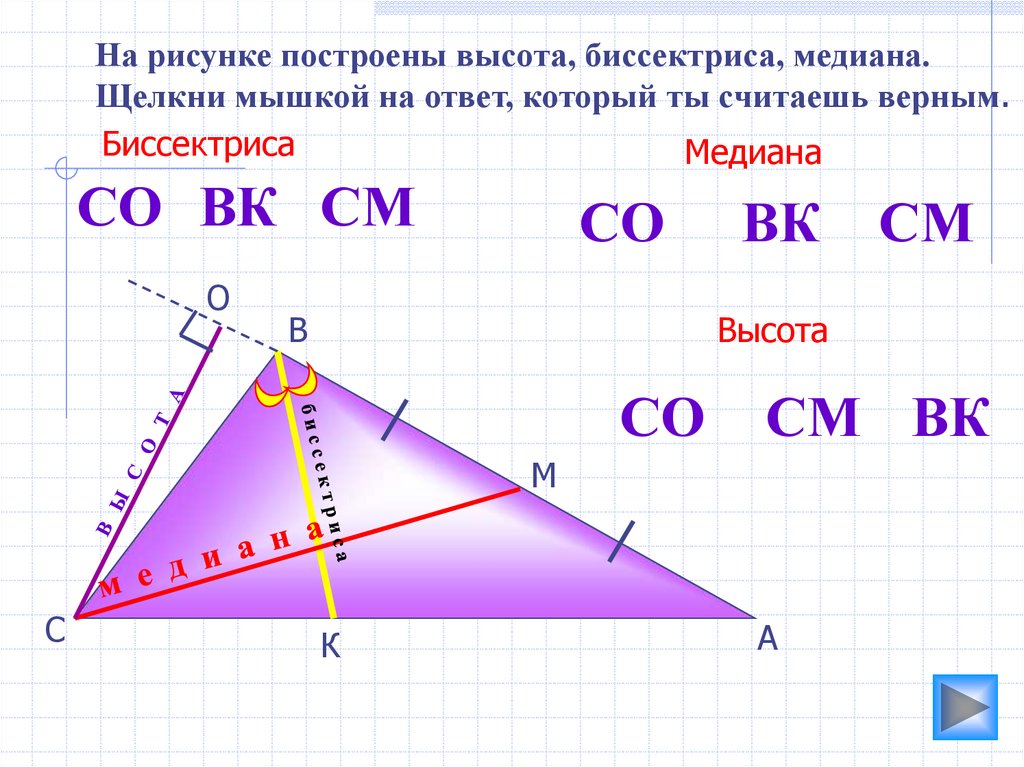
На рисунке построены высота, биссектриса, медиана.Щелкни мышкой на ответ, который ты считаешь верным.
Биссектриса
Медиана
СО ВК СМ
О
СО
В
ВК
Высота
СО
СМ ВК
М
С
СМ
К
А
9. Замечание!!!
На след слайдах изучаемсвойство медиан треугольника;
свойство высот треугольника
(остроугольного,
прямоугольного и
тупоугольного)
10.
ВQ
С
М
O
N
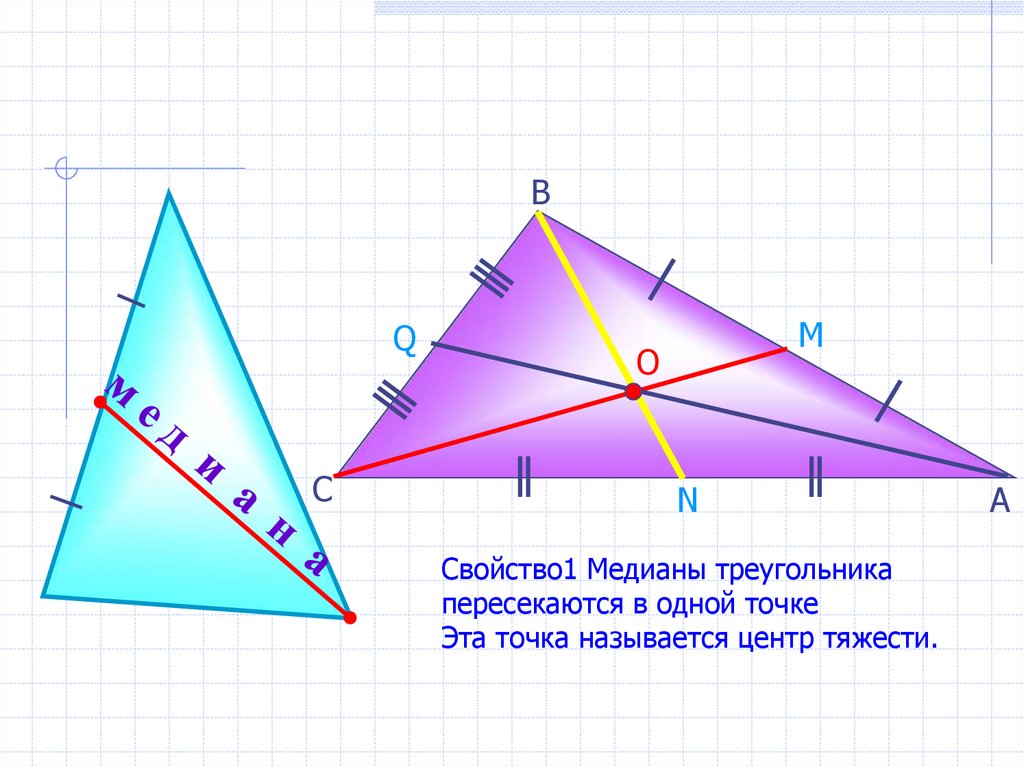
Свойство1 Медианы треугольника
пересекаются в одной точке
Эта точка называется центр тяжести.
А
11.
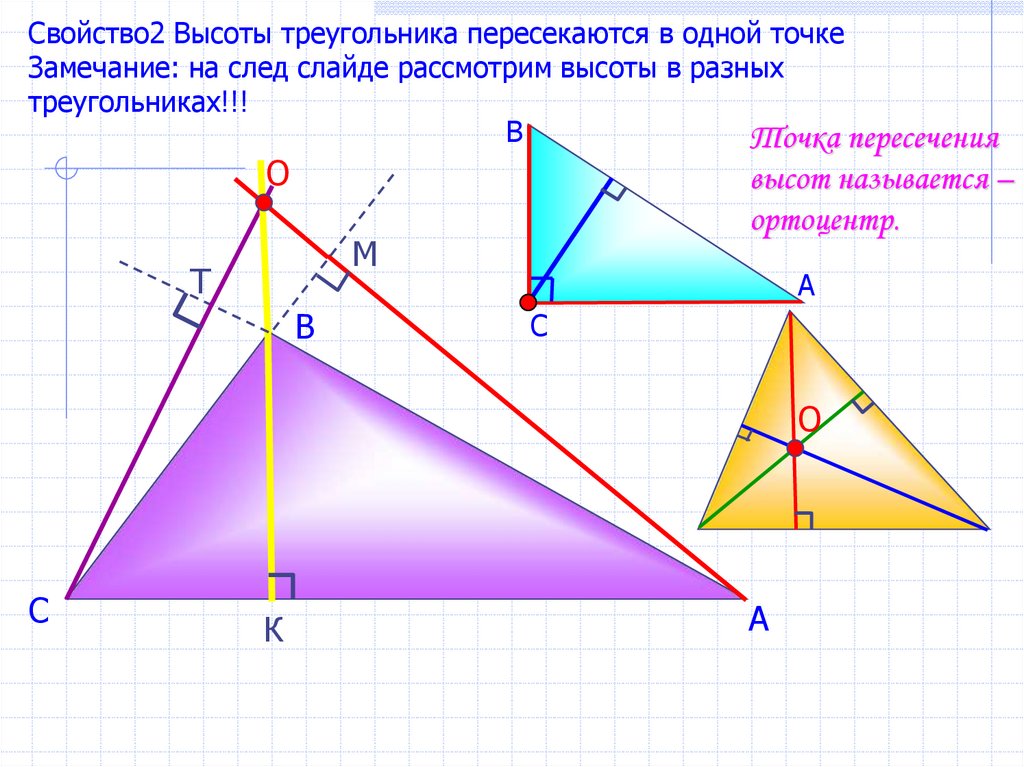
Свойство2 Высоты треугольника пересекаются в одной точкеЗамечание: на след слайде рассмотрим высоты в разных
треугольниках!!!
В
Точка пересечения
O
высот называется –
ортоцентр.
М
Т
В
А
С
O
С
К
А
12.
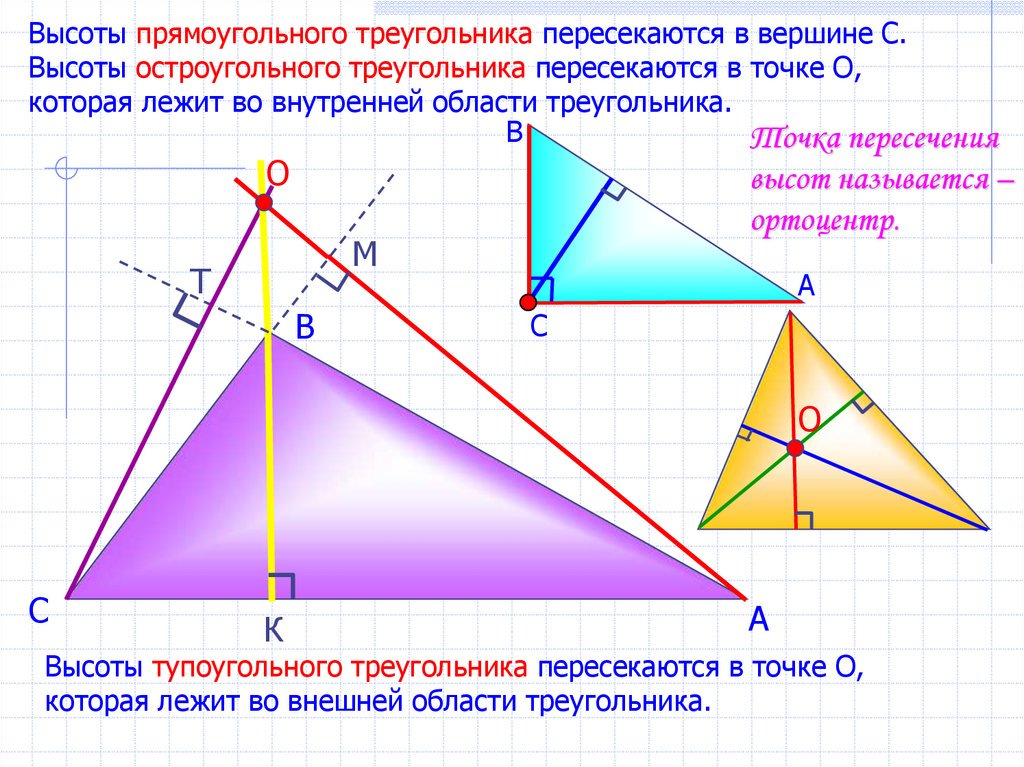
Высоты прямоугольного треугольника пересекаются в вершине С.Высоты остроугольного треугольника пересекаются в точке О,
которая лежит во внутренней области треугольника.
В
Точка пересечения
O
высот называется –
ортоцентр.
М
Т
В
А
С
O
С
К
А
Высоты тупоугольного треугольника пересекаются в точке О,
которая лежит во внешней области треугольника.
13.
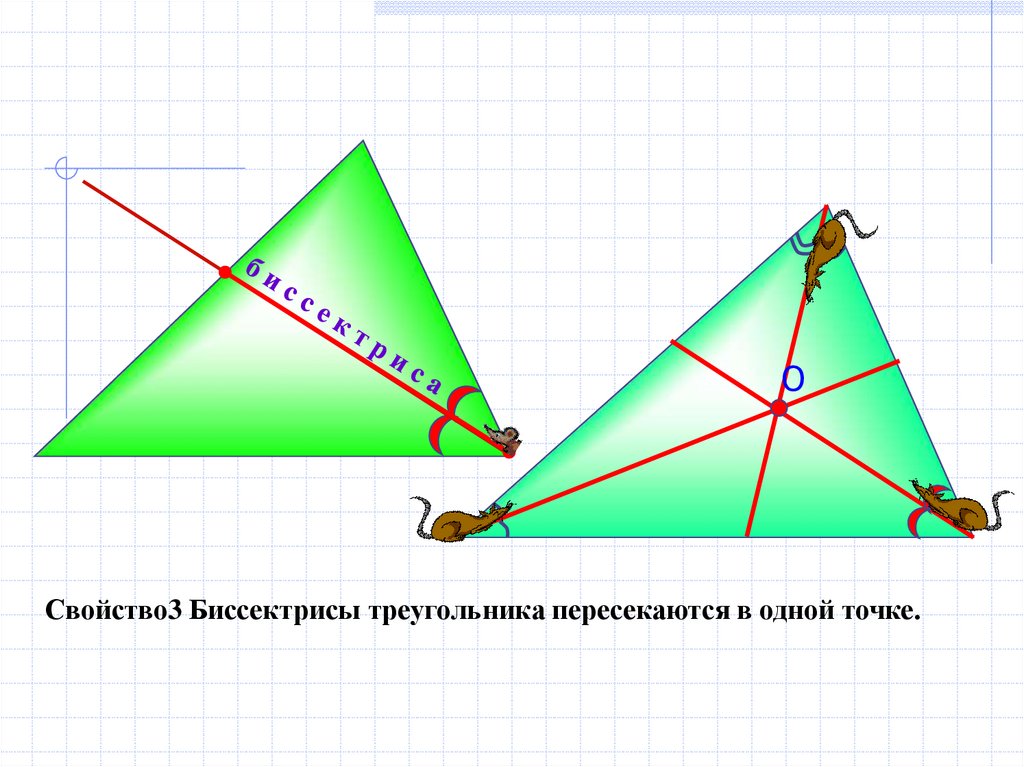
OСвойство3 Биссектрисы треугольника пересекаются в одной точке.
14. Замечание!!!
На след слайдах изучаем понятия равнобедренногои равностороннего треугольника в рисунках, а из
пункта 18 берем:
•определения равнобедренного и равностороннего
треугольника
•свойства (теоремы) равнобедренного треугольника
с доказательством!!!
15.
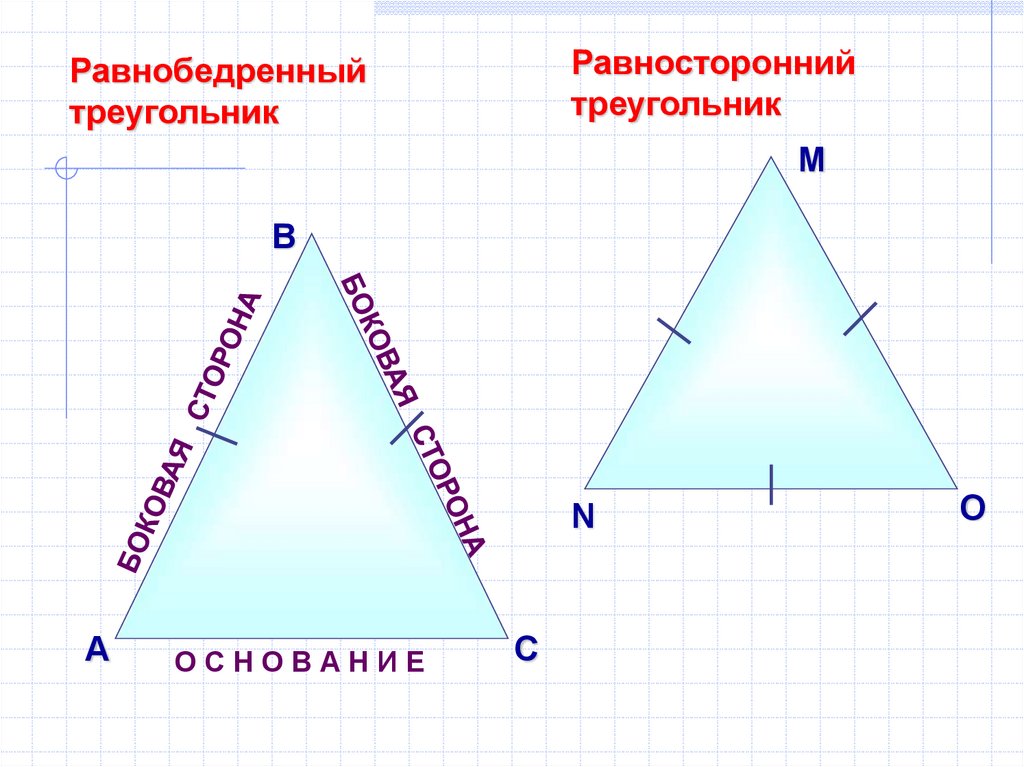
Равностороннийтреугольник
Равнобедренный
треугольник
M
В
N
А
ОСНОВАНИЕ
С
O







 Математика
Математика








