Futures and Forwards

1. CHAPTER 19

Futures Markets (40 slides)
INVESTMENTS | BODIE, KANE, MARCUS
McGraw-Hill/Irwin
Copyright © 2011 by The McGraw-Hill Companies, Inc. All rights reserved.

2. Futures and Forwards

19-2
Futures and Forwards
• Forward – a deferred-delivery sale of an
asset with the sales price agreed on
now.
• Futures - similar to forward but feature
formalized and standardized contracts.
• Key difference in futures
– Standardized contracts create liquidity
– Marked to market
– Exchange mitigates credit risk
Ex next page
INVESTMENTS | BODIE, KANE, MARCUS

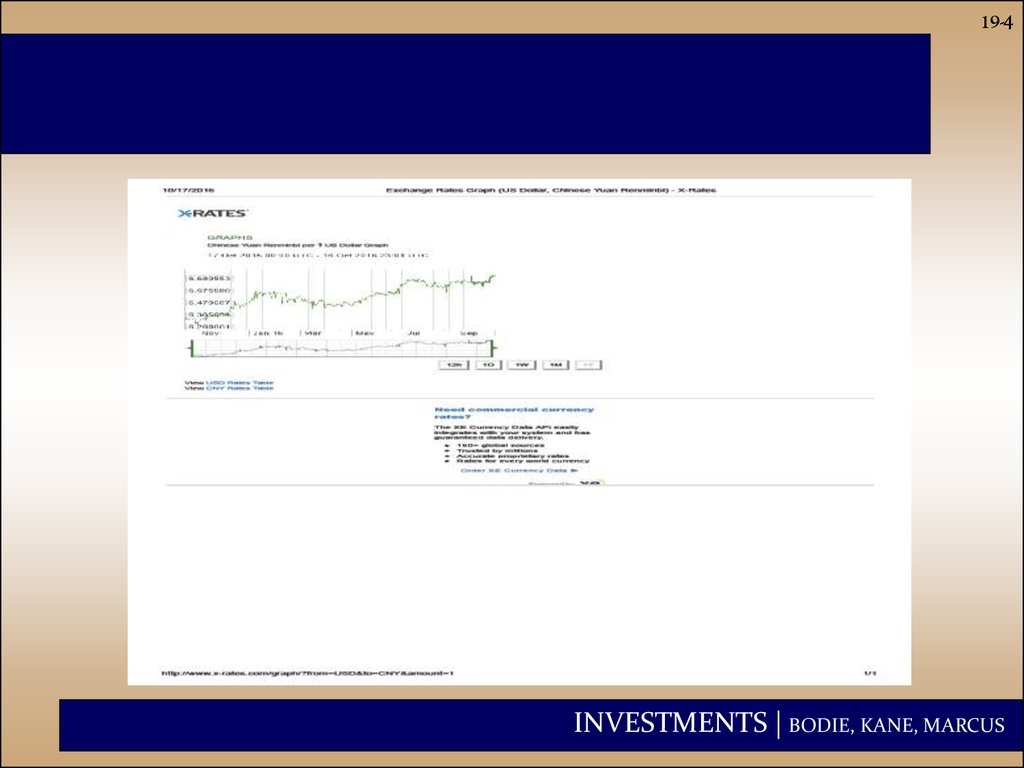
3.

19-3
INVESTMENTS | BODIE, KANE, MARCUS

4.

19-4
INVESTMENTS | BODIE, KANE, MARCUS

5.

19-5
INVESTMENTS | BODIE, KANE, MARCUS

6.

19-6
INVESTMENTS | BODIE, KANE, MARCUS

7.

19-7
INVESTMENTS | BODIE, KANE, MARCUS

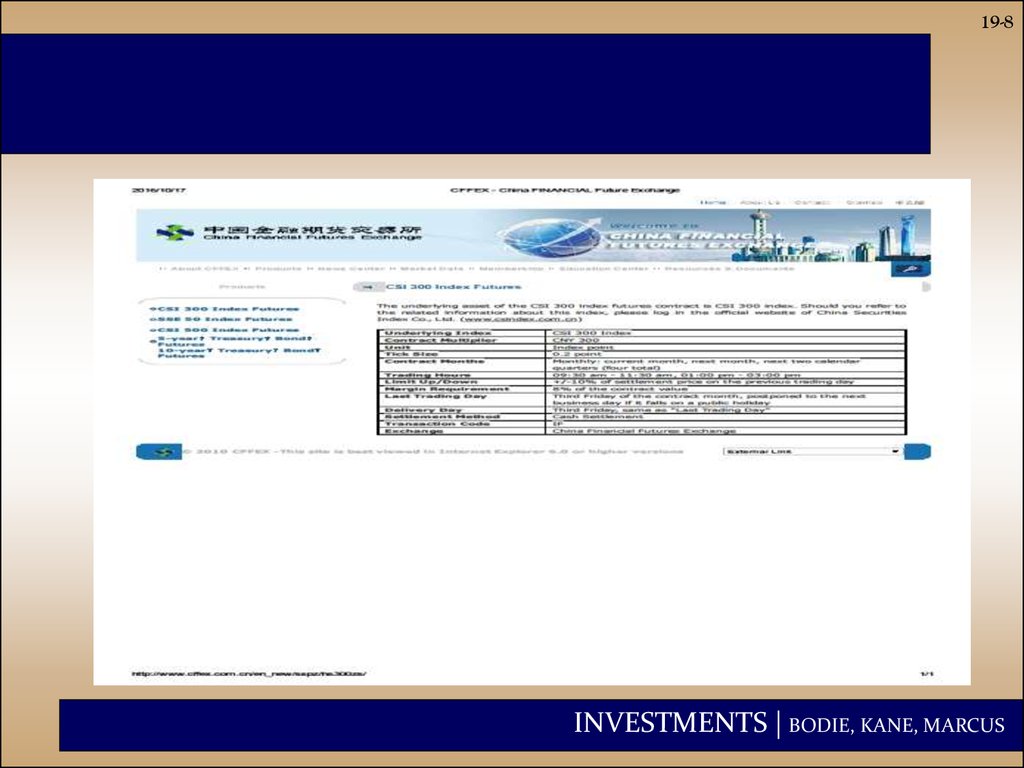
8.

19-8
INVESTMENTS | BODIE, KANE, MARCUS

9.

19-9
INVESTMENTS | BODIE, KANE, MARCUS

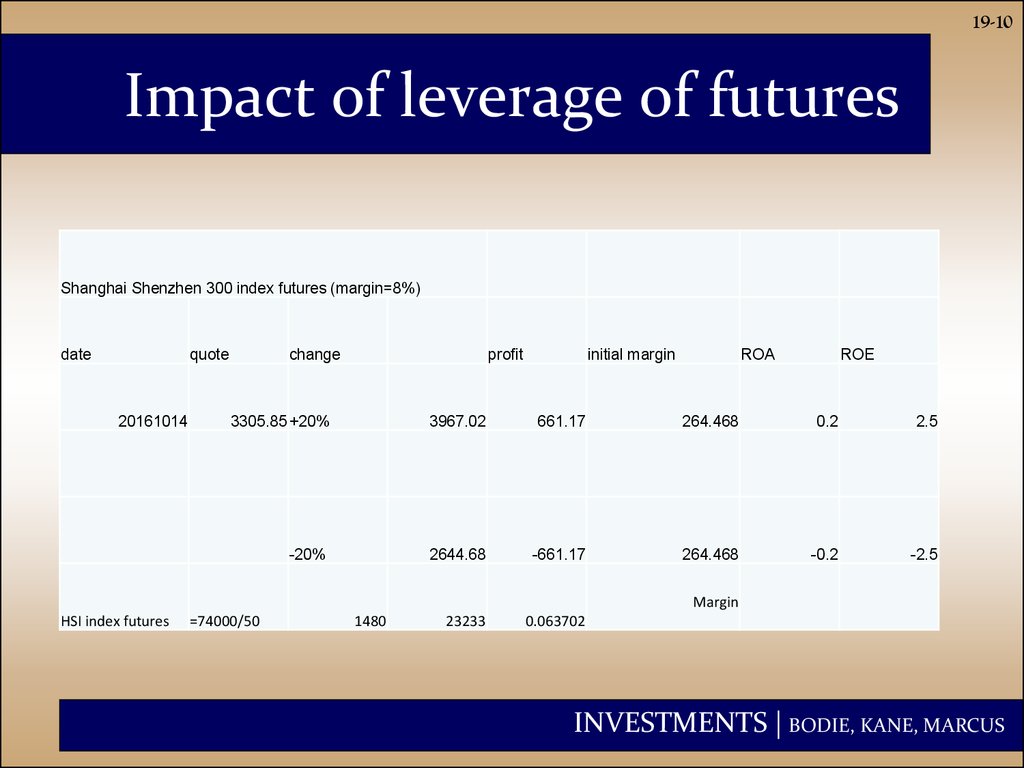
10. Impact of leverage of futures

19-10
Impact of leverage of futures
Shanghai Shenzhen 300 index futures (margin=8%)
date
quote
20161014
change
profit
initial margin
ROA
ROE
3305.85 +20%
3967.02
661.17
264.468
0.2
2.5
-20%
2644.68
-661.17
264.468
-0.2
-2.5
Margin
HSI index futures
=74000/50
1480
23233
0.063702
INVESTMENTS | BODIE, KANE, MARCUS

11. Basics of Futures Contracts

19-11
Basics of Futures Contracts
• A futures contract is the obligation to make or take
delivery of the underlying asset at a predetermined
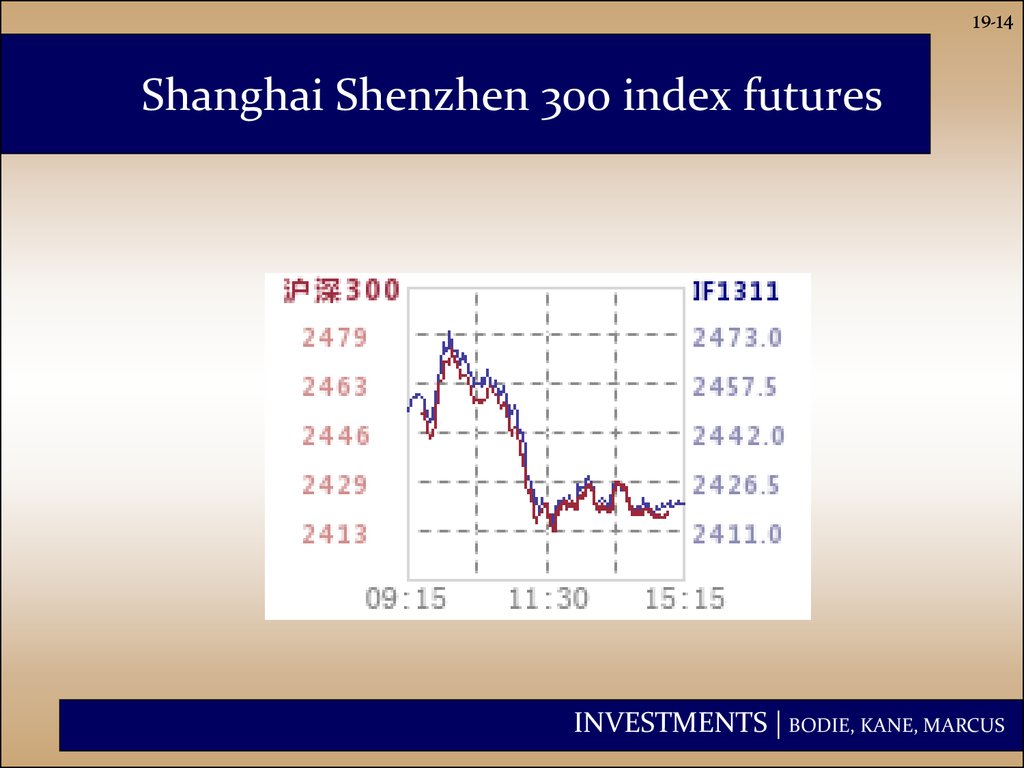
price. Shanghai Shenzhen 300 index futures next 2
pages
• Futures price – the price for the underlying asset is
determined today, but settlement is on a future
date.
• The futures contract specifies the quantity and
quality of the underlying asset and how it will be
delivered.
INVESTMENTS | BODIE, KANE, MARCUS

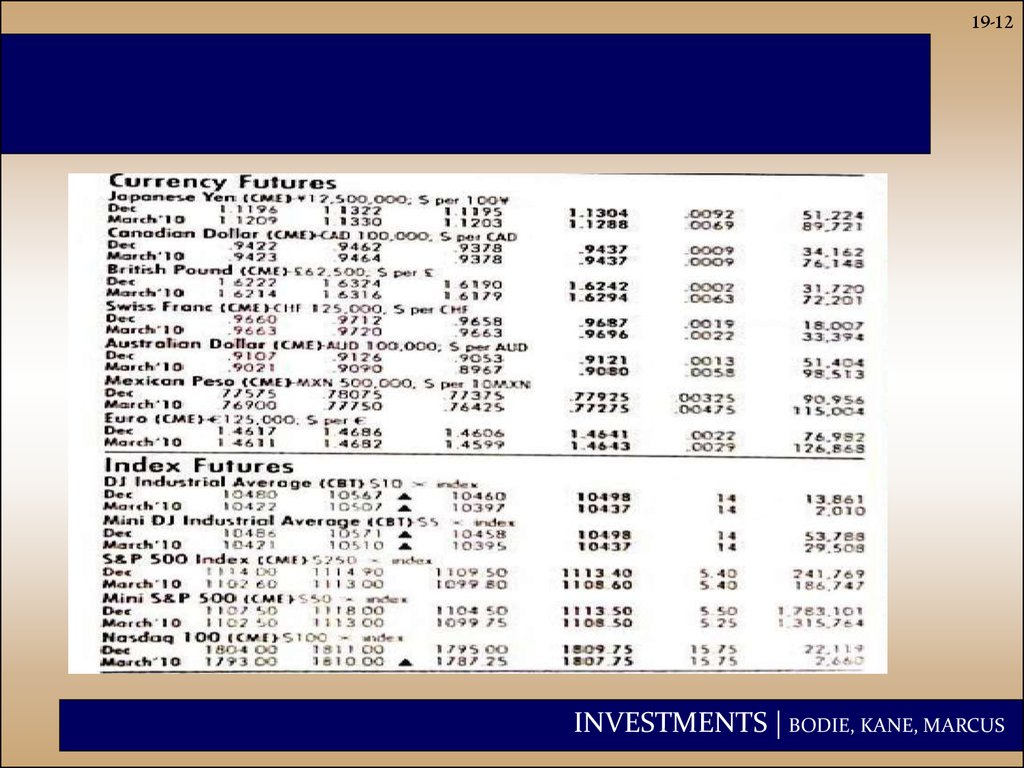
12.

19-12
INVESTMENTS | BODIE, KANE, MARCUS

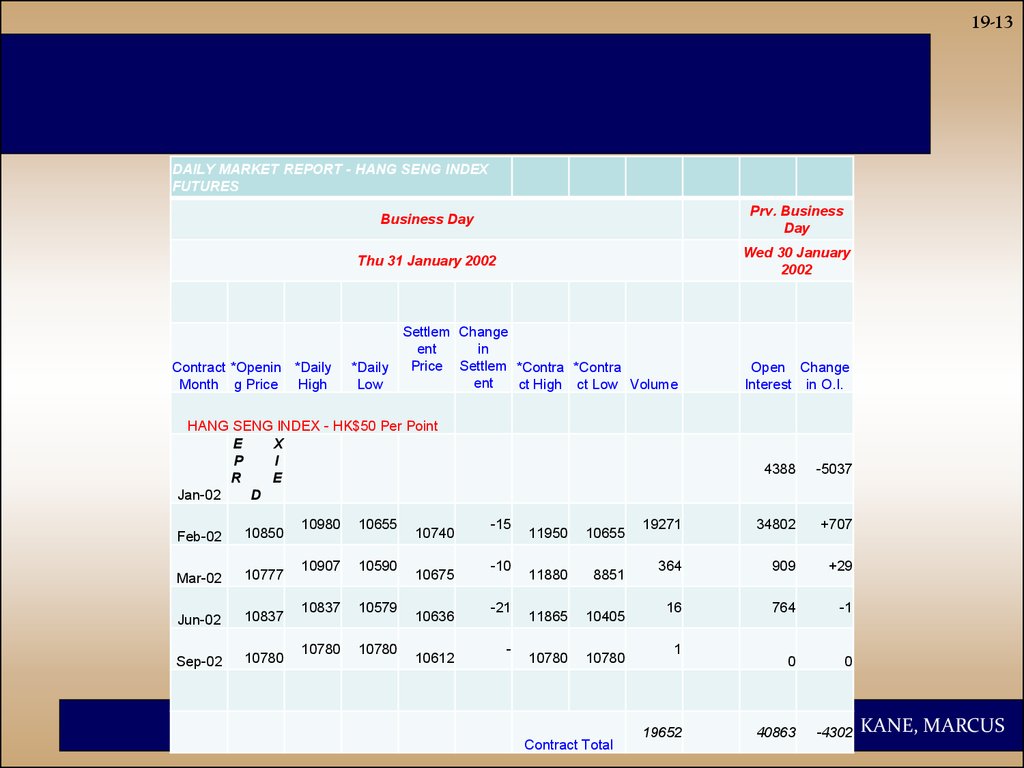
13.

19-13
DAILY MARKET REPORT - HANG SENG INDEX
FUTURES
Contract *Openin *Daily
Month g Price High
Business Day
Prv. Business
Day
Thu 31 January 2002
Wed 30 January
2002
Settlem Change
ent
in
Price Settlem *Contra *Contra
*Daily
ent
Low
ct High ct Low Volume
HANG SENG INDEX - HK$50 Per Point
E
X
P
I
R
E
D
Jan-02
Feb-02
10850
Mar-02
10777
Jun-02
10837
Sep-02
10780
10980
10655
10907
10590
10837
10579
10780
10780
10740
10675
10636
10612
-15
-10
-21
-
11950
10655
11880
8851
11865
10405
10780
10780
Open Change
Interest in O.I.
4388
-5037
19271
34802
+707
364
909
+29
16
764
-1
0
0
1
INVESTMENTS
| BODIE,
19652
40863
-4302 KANE, MARCUS
Contract Total

14. Shanghai Shenzhen 300 index futures

19-14
Shanghai Shenzhen 300 index futures
INVESTMENTS | BODIE, KANE, MARCUS

15. Dalian commodity exchange

19-15
Dalian commodity exchange
Corn
Soybean Meal
Product
LLDPE
Coking Coal
No.1 Soybeans
No.2 Soybeans
Soybean Oil
RBD Palm Olein
PVC
Coke
Iron Ore
INVESTMENTS | BODIE, KANE, MARCUS

16. Basics of Futures Contracts

19-16
Basics of Futures Contracts
• Long – a commitment to purchase the
commodity on the delivery date.
• Short – a commitment to sell the
commodity on the delivery date.
• Futures are traded on margin.
• At the time the contract is entered into, no
money changes hands.
INVESTMENTS | BODIE, KANE, MARCUS

17. Basics of Futures Contracts

19-17
Basics of Futures Contracts
• Profit to long = Spot price at maturity - Original
futures price
• Profit to short = Original futures price - Spot
price at maturity
• The futures contract is a zero-sum game, which
means gains and losses net out to zero.
INVESTMENTS | BODIE, KANE, MARCUS

18. Figure 19.2 Profits to Buyers and Sellers of Futures and Option Contracts

19-18
Figure 19.2 Profits to Buyers and Sellers
of Futures and Option Contracts
INVESTMENTS | BODIE, KANE, MARCUS

19. Figure 19.2 Conclusions

19-19
Figure 19.2 Conclusions
• Profit is zero when the ultimate spot price,
PT equals the initial futures price, F0 .
• Unlike a call option, the payoff to the long
position can be negative because the
futures trader cannot walk away from the
contract if it is not profitable.
INVESTMENTS | BODIE, KANE, MARCUS

20. Existing Contracts

19-20
Existing Contracts
• Futures contracts are traded on a wide
variety of assets in four main categories:
1.
2.
3.
4.
Agricultural commodities
Metals and minerals
Foreign currencies
Financial futures
INVESTMENTS | BODIE, KANE, MARCUS

21. Trading Mechanics

19-21
Trading Mechanics
• Electronic trading
has mostly
displaced floor
trading.
• CBOT and CME
merged in 2007 to
form CME Group.
• The exchange acts
as a clearing house
and counterparty to
both sides of the
trade.
• The net position of
the clearing house is
zero.
INVESTMENTS | BODIE, KANE, MARCUS

22. Trading Mechanics

19-22
Trading Mechanics
• Open interest is the number of contracts
outstanding.
• If you are currently long, you simply
instruct your broker to enter the short side
of a contract to close out your position.
• Most futures contracts are closed out by
reversing trades.
• Only 1-3% of contracts result in actual
delivery of the underlying commodity.
INVESTMENTS | BODIE, KANE, MARCUS

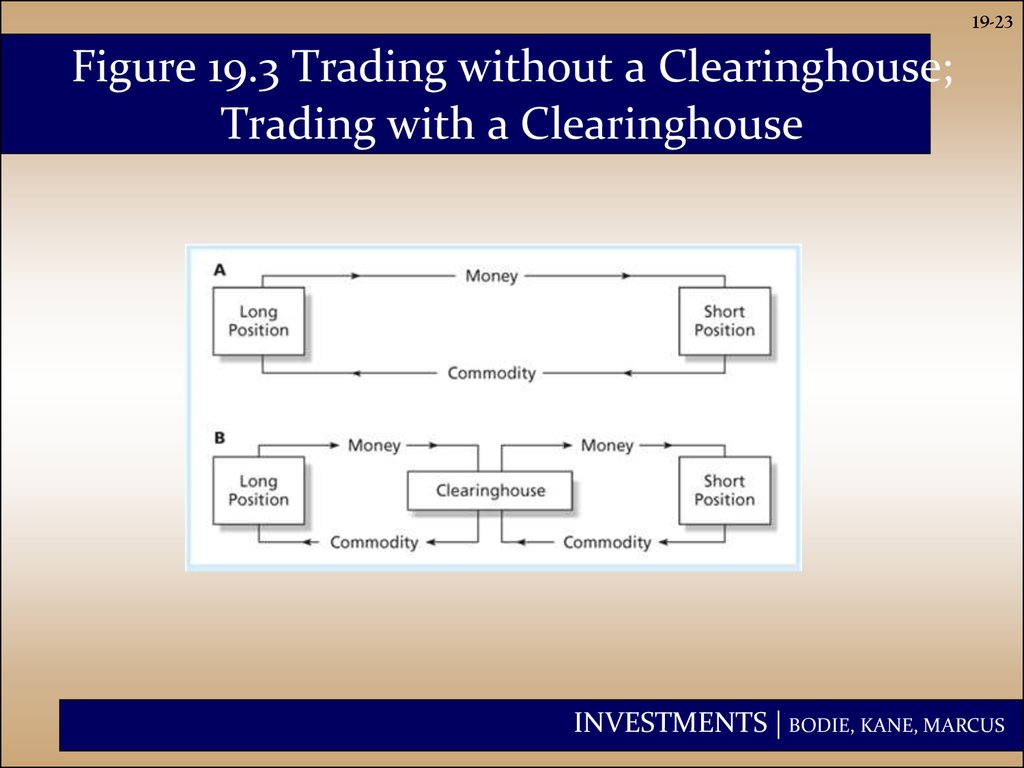
23. Figure 19.3 Trading without a Clearinghouse; Trading with a Clearinghouse

19-23
Figure 19.3 Trading without a Clearinghouse;
Trading with a Clearinghouse
INVESTMENTS | BODIE, KANE, MARCUS

24. Margin and Marking to Market

19-24
Margin and Marking to Market
• Marking to Market - each day the profits or
losses from the new futures price are paid
over or subtracted from the account
• Convergence of Price - as maturity
approaches the spot and futures price
converge
INVESTMENTS | BODIE, KANE, MARCUS

25. Margin and Trading Arrangements

19-25
Margin and Trading Arrangements
• Initial Margin - funds or interest-earning
securities deposited to provide capital to
absorb losses
• Maintenance margin - an established value
below which a trader’s margin may not fall
• Margin call - when the maintenance margin
is reached, broker will ask for additional
margin funds
INVESTMENTS | BODIE, KANE, MARCUS

26. Trading Strategies

19-26
Trading Strategies
Speculators
• seek to profit from price
movement
– short - believe price will fall
– long - believe price will rise
Hedgers
• seek protection from price
movement
– long hedge - protecting
against a rise in purchase
price
– short hedge - protecting
against a fall in selling price
INVESTMENTS | BODIE, KANE, MARCUS

27. Basis and Basis Risk

19-27
Basis and Basis Risk
• Basis - the difference between the
futures price and the spot price, FT –
PT
• The convergence property says FT –
PT= 0 at maturity.
INVESTMENTS | BODIE, KANE, MARCUS

28. Basis and Basis Risk

19-28
Basis and Basis Risk
• Before maturity, FT may differ
substantially from the current spot
price.
• Basis Risk - variability in the basis
means that gains and losses on the
contract and the asset may not
perfectly offset if liquidated before
maturity.
INVESTMENTS | BODIE, KANE, MARCUS

29. Futures Pricing

19-29
Futures Pricing
Spot-futures parity theorem - two ways
to acquire an asset for some date in the
future:
1. Purchase it now and store it
2. Take a long position in futures
•These two strategies must have the
same market determined costs
INVESTMENTS | BODIE, KANE, MARCUS

30. Spot-Futures Parity Theorem

19-30
Spot-Futures Parity Theorem
• With a perfect hedge, the futures payoff
is certain -- there is no risk.
• A perfect hedge should earn the
riskless rate of return.
• This relationship can be used to
develop the futures pricing relationship.
INVESTMENTS | BODIE, KANE, MARCUS

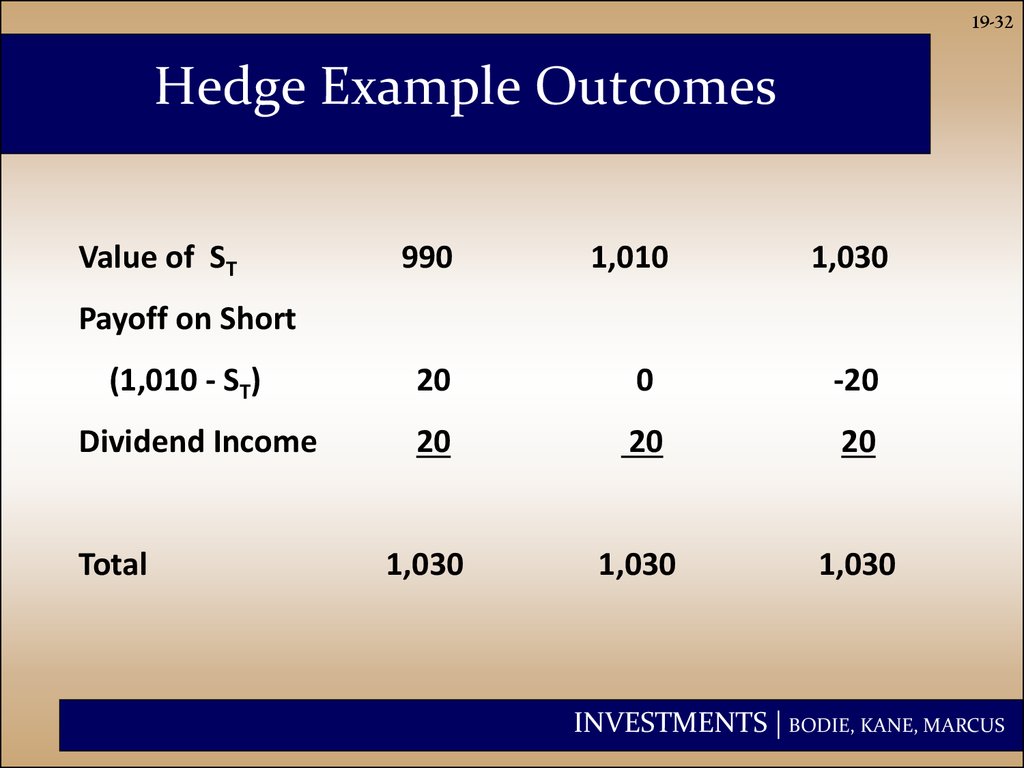
31. Hedge Example: Section 19.4

19-31
Hedge Example: Section 19.4
• Investor holds $1000 in a mutual fund
indexed to the S&P 500.
• Assume dividends of $20 will be paid on
the index fund at the end of the year.
• A futures contract with delivery in one
year is available for $1,010.
• The investor hedges by selling or
shorting one contract .
INVESTMENTS | BODIE, KANE, MARCUS

32. Hedge Example Outcomes

19-32
Hedge Example Outcomes
Value of ST
990
1,010
1,030
Payoff on Short
(1,010 - ST)
Dividend Income
Total
20
0
-20
20
20
20
1,030
1,030
1,030
INVESTMENTS | BODIE, KANE, MARCUS

33. Rate of Return for the Hedge

19-33
Rate of Return for the Hedge
( F0 D ) S 0
S0
(1,010 20) 1,000
3%
1,000
INVESTMENTS | BODIE, KANE, MARCUS

34. The Spot-Futures Parity Theorem

19-34
The Spot-Futures Parity Theorem
( F0 D ) S 0
rf
S0
Rearranging terms
F0 S 0 (1 r f ) D S 0 (1 r f d )
d D
S0
INVESTMENTS | BODIE, KANE, MARCUS

35. Arbitrage Possibilities

19-35
Arbitrage Possibilities
• If spot-futures parity is not observed,
then arbitrage is possible.
• If the futures price is too high, short the
futures and acquire the stock by
borrowing the money at the risk free rate.
• If the futures price is too low, go long
futures, short the stock and invest the
proceeds at the risk free rate.
INVESTMENTS | BODIE, KANE, MARCUS

36. Spread Pricing: Parity for Spreads

19-36
Spread Pricing: Parity for Spreads
T
F (T1 ) S0 (1 rf d ) 1
T
F (T2 ) S0 (1 rf d ) 2
F (T2 ) F (T1 )(1 rf d )
( T 2 T 1 )
INVESTMENTS | BODIE, KANE, MARCUS

37. Spreads

19-37
Spreads
• If the risk-free rate is greater than the
dividend yield (rf > d), then the futures
price will be higher on longer maturity
contracts.
• If rf < d, longer maturity futures prices will
be lower.
• For futures contracts on commodities that
pay no dividend, d=0, F must increase as
time to maturity increases.
INVESTMENTS | BODIE, KANE, MARCUS

38. Figure 19.6 Gold Futures Prices

19-38
Figure 19.6 Gold Futures Prices
INVESTMENTS | BODIE, KANE, MARCUS

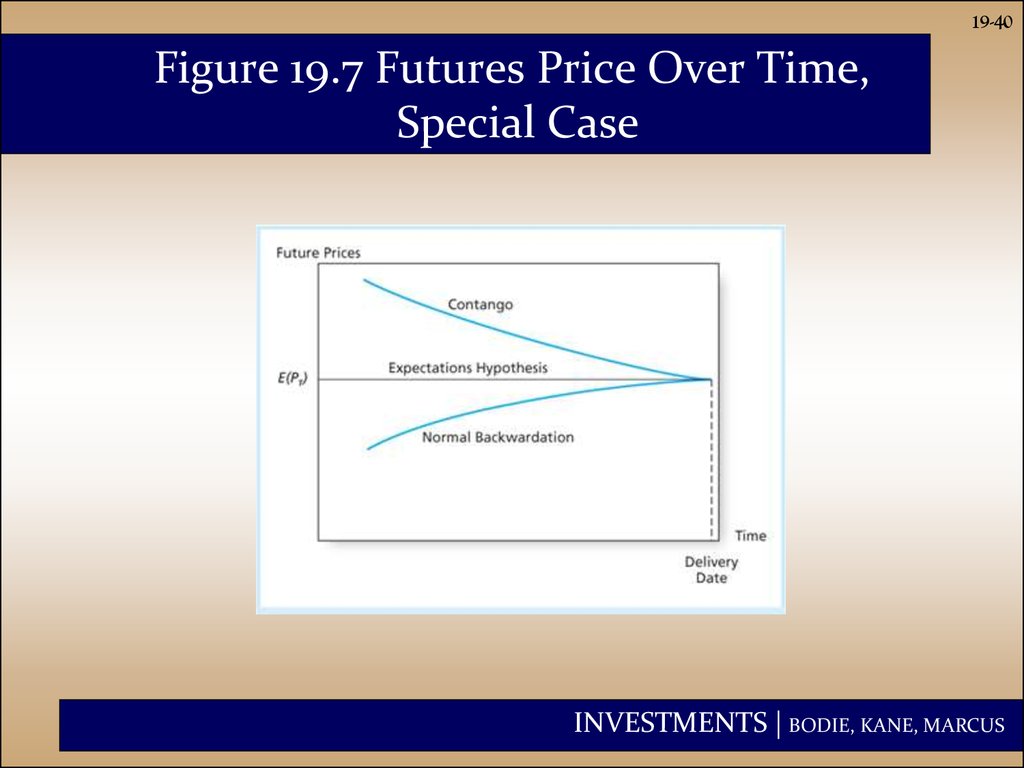
39. Futures Prices vs. Expected Spot Prices

19-39
Futures Prices vs. Expected Spot
Prices
• Expectations F0=E(PT), PT = future spot price
• Normal Backwardation: futures price bid down to a level
below E(PT) as speculators needs a profit of F0-E(PT) to
long the contract
• Contango: F0<E(PT) as the natural hedgers are the
purchasers of a commodity and want to hedge their
purchase at T
• Modern Portfolio Theory: if commodity prices pose
positive systematic risk, futures prices must be lower
than expected spot prices: F0=E(PT)[(1/rf)/(1+k)]T
INVESTMENTS | BODIE, KANE, MARCUS

40. Figure 19.7 Futures Price Over Time, Special Case

19-40
Figure 19.7 Futures Price Over Time,
Special Case
INVESTMENTS | BODIE, KANE, MARCUS