Похожие презентации:
Задачи управления запасами
1. Задачи управления запасами
Жданов И.Д.ФО-430501
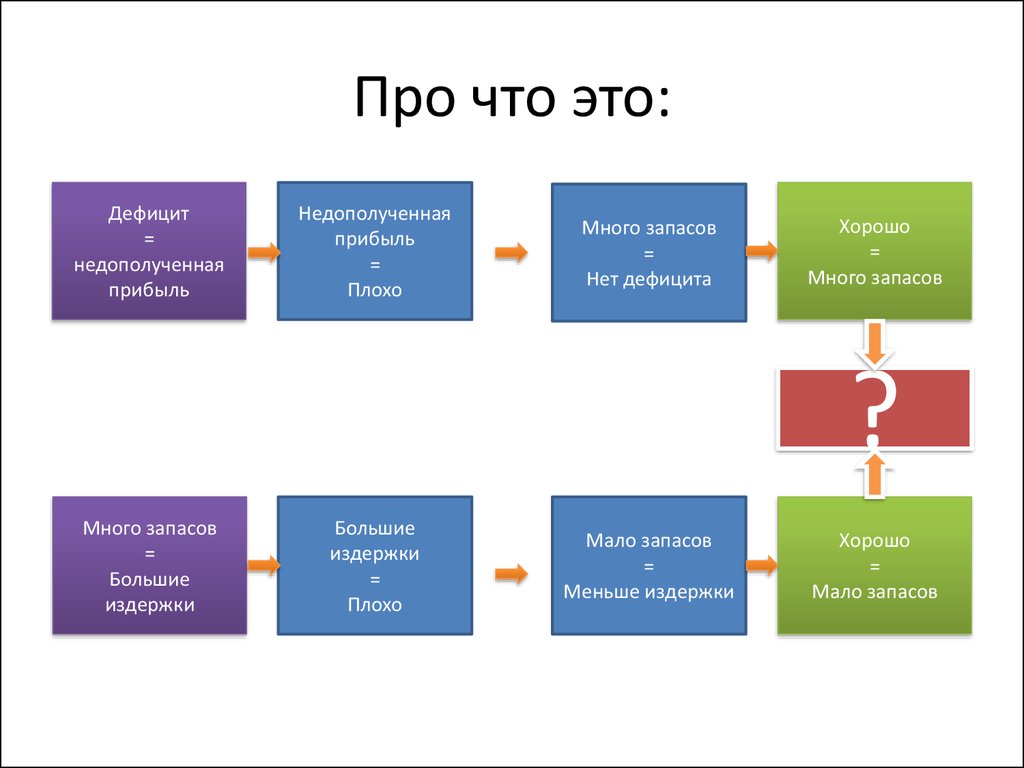
2. Про что это:
Дефицит=
недополученная
прибыль
Недополученная
прибыль
=
Плохо
Много запасов
=
Нет дефицита
Хорошо
=
Много запасов
?
Много запасов
=
Большие
издержки
Большие
издержки
=
Плохо
Мало запасов
=
Меньше издержки
Хорошо
=
Мало запасов
3.
Хорошо = прибыль максимальна4. Почему этим стоит интересоваться:
• Управление запасами – ключевая логистическая функция, на долюкоторой, согласно различным источникам, вместе с транспортировкой
приходится более 50% логистических издержек
• Никто не станет заботиться о вашем бизнесе так же старательно как о
нём будете заботиться вы
• «Специалист по управлению товарными запасами» стоит от 50000 –
200000 рублей в зависимости от статуса компании.
5. Теория управления запасами (УЗ)
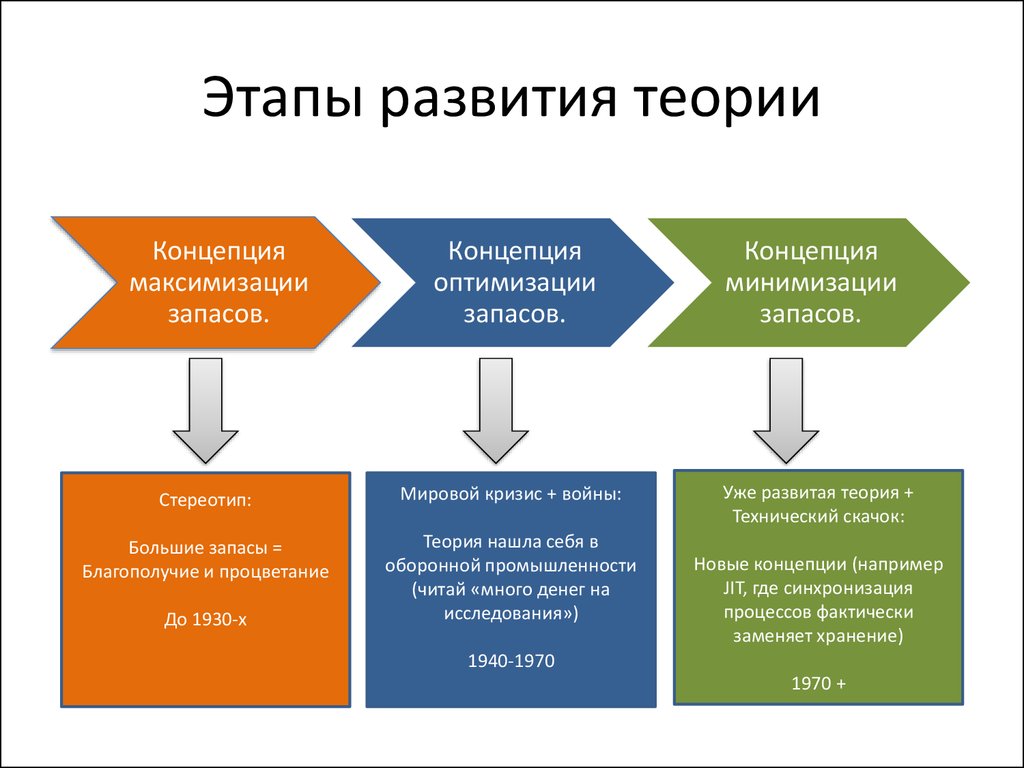
6. Этапы развития теории
Концепциямаксимизации
запасов.
Концепция
оптимизации
запасов.
Стереотип:
Мировой кризис + войны:
Большие запасы =
Благополучие и процветание
Теория нашла себя в
оборонной промышленности
(читай «много денег на
исследования»)
До 1930-х
Концепция
минимизации
запасов.
Уже развитая теория +
Технический скачок:
Новые концепции (например
JIT, где синхронизация
процессов фактически
заменяет хранение)
1940-1970
1970 +
7. Небольшой итог
• Теория активно развивается• Многие компании в этом заинтересованы
• Эффективное управление запасами позволяет достаточно хорошо
повышать чистую прибыль
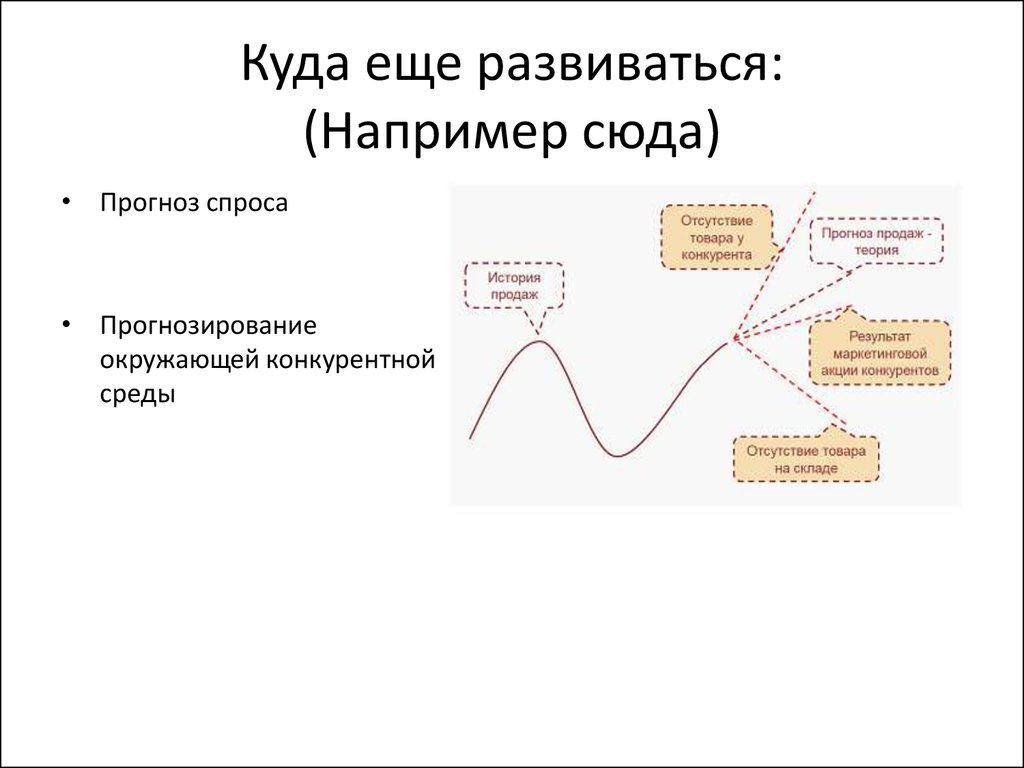
8. Куда еще развиваться: (Например сюда)
• Прогноз спроса• Прогнозирование
окружающей конкурентной
среды
9. Пример задачи
• Объем продажи некоторого магазина составляет в год 500 упаковоксупа в пакетах. Величина спроса равномерно распределяется в
течение года. Цена покупки одного пакета равна 2 руб. За доставку
заказа владелец магазина должен заплатить 10 руб. Время доставки
заказа от поставщика составляет 12 рабочих дней (при 6-дневной
рабочей неделе). По оценкам специалистов, издержки хранения в год
составляют 40 коп. за один пакет. Необходимо определить: сколько
пакетов должен заказывать владелец магазина для одной поставки;
частоту заказов; точку заказа. Известно, что магазин работает 300
дней в году.
10. Модель и формула оптимального размера заказа (модель Уилсона)
Математика позволяет найти оптимальный уровень запасов товара,минимизирующий суммарные затраты на покупку, оформление и
доставку заказа, а также хранение товара.
Для того, чтоб использовать модель Уилсона необходимо собрать
некоторое количество данных (постоянных величин)
Затраты на заказы
Затраты на содержание запасов
Расходы на закупку каждой партии
товара
Налоги
Затраты на контроль наличия товара
Страхование
Высылка заказа
Потери от износа
Раскладка товара по местам
хранения
Потери от устаревания, порчи
И т.п.
И т.п.
11.
Модель Уилсона и помогает найти оптимальное для заказа количествопродукта для запасов, при котором издержки на его обработку и
хранение минимальны.
Это называется «экономически обоснованный заказ»
Чтобы рассчитать ЭОЗ, нужно знать издержки пополнения заказа (К),
издержки хранения (S), ежедневный спрос (v), стоимость единицы товара
в закупочных ценах (s) и общее количество дней, когда товар находится в
продаже за год (t).
12.
Модель Уилсона описывает закупку, которая характеризуется некоторымиограничения и имеет следующие условия:
• Модель применяется для одного вида товара.
• Уровень спроса постоянен в течение планового периода времени.
• Средний уровень запаса составляет половину размера заказа.
• Интервал времени между поставками постоянен.
• Время доставки постоянно.
• Стоимость хранения запасов определяется, исходя из среднего размера запаса.
• Затраты на размещение заказа постоянны.
• Цены на закупку постоянны.
• Каждый заказ приходит отдельной поставкой.
• Поставка приходуется на склад одновременно, то есть в рамках одного учетного
периода (так называемая мгновенная поставка) (см. рисунок 4).
• Вследствие постоянного темпа потребления и отгрузки приемка осуществляется в
момент времени, когда уровень запаса равен нулю.
• Транспортный (транзитный), подготовительный, сезонный и страховой
(гарантийный) запасы отсутствуют.
• Отсутствуют ограничения по производственным мощностям склада.
• Отсутствуют потери от дефицита.
13. Коротко
• Много ограничений -> довольно-такичастный случай и стоит понимать, в каких
её можно использовать.
• Тем не менее, модель применима в жизни
достаточно часто и неплохо служит для
объяснения сути
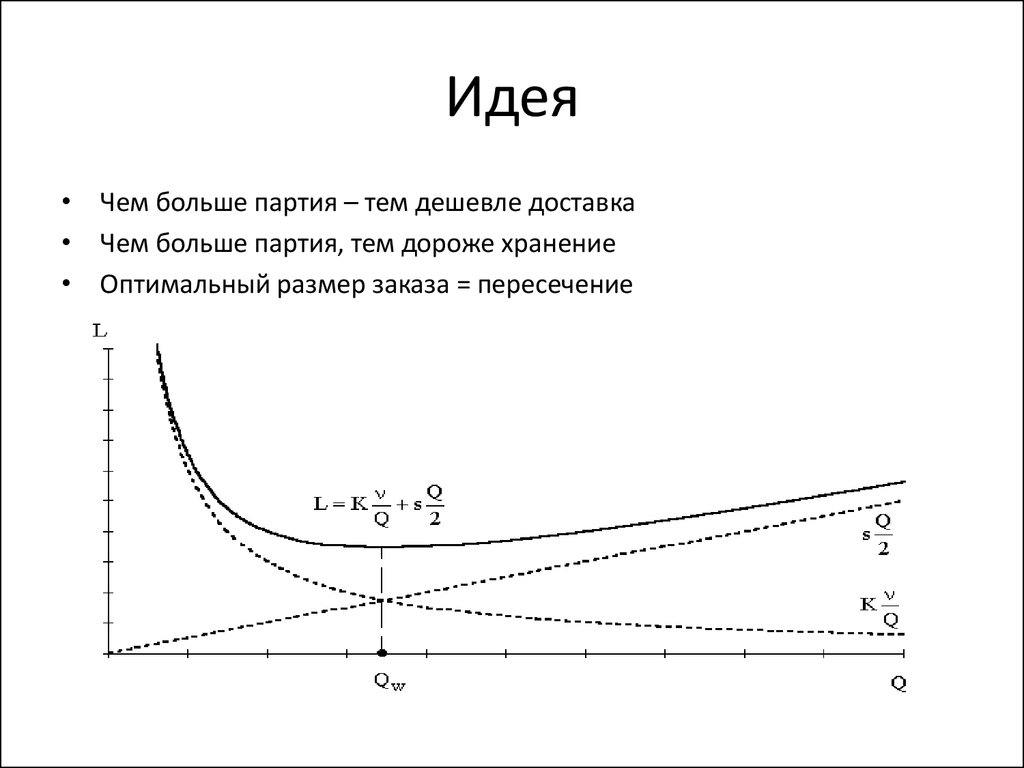
14. Идея
• Чем больше партия – тем дешевле доставка• Чем больше партия, тем дороже хранение
• Оптимальный размер заказа = пересечение
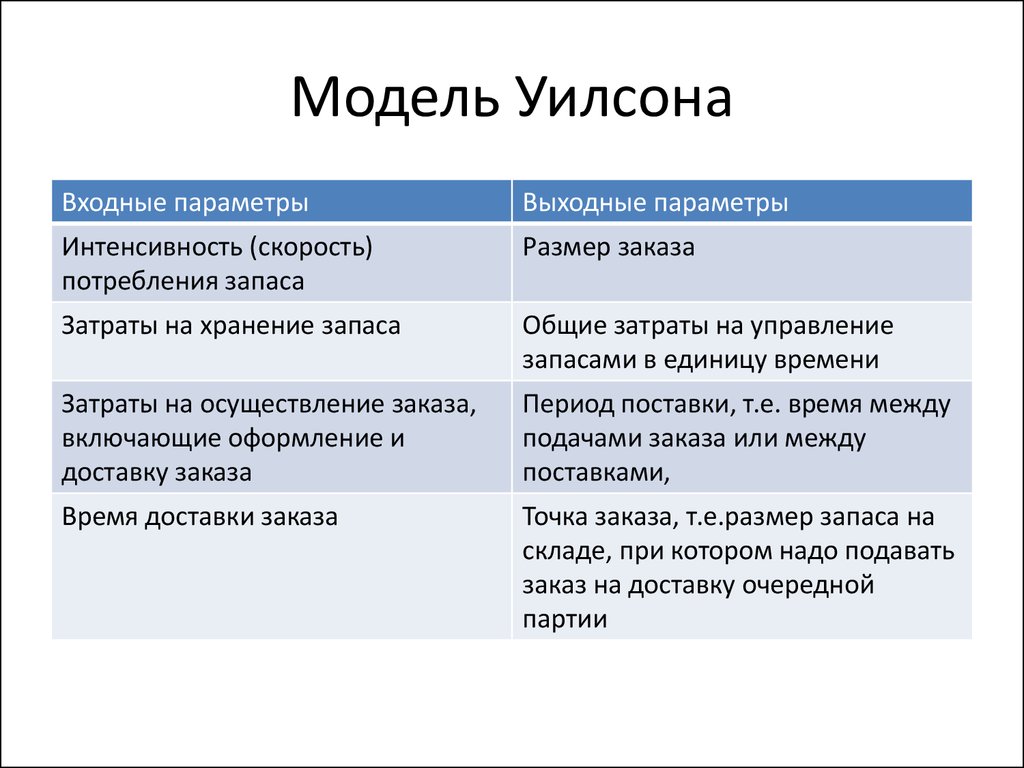
15. Модель Уилсона
Входные параметрыВыходные параметры
Интенсивность (скорость)
потребления запаса
Размер заказа
Затраты на хранение запаса
Общие затраты на управление
запасами в единицу времени
Затраты на осуществление заказа,
включающие оформление и
доставку заказа
Период поставки, т.е. время между
подачами заказа или между
поставками,
Время доставки заказа
Точка заказа, т.е.размер запаса на
складе, при котором надо подавать
заказ на доставку очередной
партии
16.
Формулы модели Уилсона(формула Уилсона),
где
– оптимальный размер заказа в модели Уилсона;
;
;
.
17. Вспоминаем задачу
• Объем продажи некоторого магазина составляет в год 500 упаковоксупа в пакетах. Величина спроса равномерно распределяется в
течение года. Цена покупки одного пакета равна 2 руб. За доставку
заказа владелец магазина должен заплатить 10 руб. Время доставки
заказа от поставщика составляет 12 рабочих дней (при 6-дневной
рабочей неделе). По оценкам специалистов, издержки хранения в год
составляют 40 коп. за один пакет. Необходимо определить: сколько
пакетов должен заказывать владелец магазина для одной поставки;
частоту заказов; точку заказа. Известно, что магазин работает 300
дней в году.
18. Решение
Примем за единицу времени год, тогдашт. пакетов в
год,
руб.,
. Поскольку пакеты супа заказываются
со склада поставщика, а не производятся самостоятельно, то будем
использовать модель Уилсона.
штук.
Поскольку число пакетов должно быть целым, то будем заказывать по 158
штук. При расчете других параметров задачи будем использовать
не
, а Q=158. Годовые затраты на УЗ равны
рублей в год.
19.
Подачу каждого нового заказа должна производиться черезгода.
Поскольку известно, что в данном случае год равен 300 рабочим дням, то
рабочих дней.
Заказ следует подавать при уровне запаса, равном
пакетам,
т.е. эти 20 пакетов будут проданы в течение 12 дней, пока будет доставляться
заказ.














 Менеджмент
Менеджмент








