Похожие презентации:
Молекулярно-кинетическая теория
1.
Лекция 9МОЛЕКУЛЯРНОКИНЕТИЧЕСКАЯ ТЕОРИЯ
Вопросы:
1. Физическая модель идеального газа.
Основное уравнение МКТ газов
(уравнение Клаузиуса).
2. Закон равномерного распределения
энергии по степеням свободы молекул.
3. Реальные газы.
2.
Молекулярная физика – раздел, в котором изучаютсястроение и свойства вещества исходя из молекулярнокинетических представлений:
• все вещества состоят из мельчайших частиц (атомов и
молекул);
• эти частицы находятся в состоянии непрерывного
хаотического теплового движения;
• между частицами существуют силы взаимодействия.
СтатистиСтатистический
ческий
Термодинамический
Термодинамическая
система
Методы исследования
Два метода:
• статистический (оперирует вероятностными закономерностями и
средними значениями величин всего ансамбля частиц);
• термодинамический (оперирует
интегральными величинами системы – объемом, температурой, давлением – на основе обмена энергией).
3.
Основные понятия МКТКоличество вещества – физическая
величина, определяемая числом структурных
элементов (атомов или молекул), из которых
состоит вещество.
Единицей количества вещества
является 1 моль:
[ ] = моль.
1 моль – это количество вещества, в котором
содержится такое же число структурных
частиц, как и в 0,012 кг углерода.
Количество структурных частиц в одном
моле любого вещества одинаково и
называется числом (постоянной) Авогадро:
NA = 6,02 1023 моль-1.
Молярная масса µ –
масса одного моля;
[µ] = кг/моль.
m
Михаил
Васильевич
Ломоносов
(1711 – 1765)
Амедео
Авогадро
(1776 – 1856)
N где N – число
,
N А молекул газа.
4.
Базовая физическая модель МКТ – идеальный газ –идеализированная система (ансамбль) частиц, обладающая
следующими свойствами:
• суммарный собственный объем частиц много меньше
размеров сосуда, в котором они находятся;
• потенциальная энергия взаимодействия частиц равна
нулю;
• столкновение частиц друг с другом и со стенками сосуда
подчиняется законам абсолютно упругого столкновения.
Уравнение состояния (УС) – уравнение f(p,V,T) = 0, связывающее параметры состояния: давление р, объем V и температуру Т.
pV
const – УС идеального газа
T
в форме Клапейрона. (1)
рV = νRT
– УС Менделеева – Клапейрона
для произвольной массы газа m (2)
R = 8,31 Дж/(моль·К) – универсальная газовая постоянная.
5.
Преобразуем уравнение Менделеева-Клапейрона(поделим на V ) с учетом обозначений:
N
– число молей газа;
NА
23
N A 6,02 10 1 моль – число Авогадро;
R
23 Дж − постоянная
k
1,38 10
Больцмана.
NA
К
N
n − концентрация молекул газа.
V
Получаем еще одну форму записи
УС идеального газа: (3)
p=
Дмитрий
Иванович
Менделеев
(1834 – 1907)
nkT
Давление идеального газа при данной
температуре определяется только числом
молекул в единице объема и не зависит от
рода молекул.
Людвиг
Больцман
(1844 – 1906)
6.
Газовые законыЗакон Дальтона для смеси идеальных газов:
p pi (давление смеси идеальных газов
равно сумме парциальных давлений
i
газов, входящих в состав смеси).
Парциальные давления газов – это давления,
которые имели бы газы этой смеси, если бы Джон Дальтон
(1766 – 1844)
они заполняли объем по отдельности.
Частные случаи уравнения Менделеева – Клапейрона
(для т = const.):
1. T
const. pV const.
изотермический процесс
(закон Бойля – Мариотта)
V
p
p
T2 >T1
0
T1
T2
V
0
T1 T2
T
0 T1
T2
T
7.
2.p const.
изобарный процесс
(закон Гей-Люссака)
p
p
V
0
3.
T V const.
р2
р2
p1
р1
V
0
V const.
р1
р2 > p1
T 0
T
p T const.
изохорный процесс
(закон Шарля)
p
p
V
V1
V2
0
V1
V2
V 0
T 0
V2
V1
T
8.
Давление газа с точки зрения МКТИсходя из молекулярно-кинетических представлений
и 2-го закона Ньютона можно заключить, что давление, оказываемое газом на стенки сосуда, обусловлено
передачей молекулами импульса стенке при столкновениях.
9.
кв2
i i
vср.кв.
N
3kT
mмол
1
p nmмол кв
3
2
mмол
пост
кв
2
2
3RT
− средняя квадратичная
скорость молекул газа.
2 mмол кв
n
3
2
2
2
n пост
3
3
kT − средняя кинетическая энергия
2
поступательного движения
молекул газа.
– уравнение Клаузиуса
(основное уравнение МКТ газов)
Давление идеального газа численно равно
2/3 средней кинетической энергии поступаРудольф
тельного движения молекул, находящихся в
Клаузиус
единичном объеме.
(1822 – 1888)
2
p n пост
3
10.
Закон равномерного распределения энергиипо степеням свободы молекул
Поступательно движутся одноатомные молекулы. Двух- и
многоатомные молекулы, кроме поступательного, совершают
также вращательное и колебательное движения.
Числом степеней свободы i материального
объекта называется число независимых координат, однозначно определяющих положение
этого объекта в пространстве.
Число атомов в молекуле
Число степеней свободы i
(без колебательных)
1
2
3
3
5
6
Закон равнораспределения. Энергия молекулы равномерно распределяется по степеням свободы: на каждую
степень свободы молекулы приходится в среднем одинаковая кинетическая энергия, равная ½kT.
11.
Для средней энергии молекулы получается выражение:мол
i
kT
2
− число степеней свободы
молекулы.
Колебательная степень свободы обладает вдвое большим «весом», потому что на нее приходится не только
кинетическая энергия (как в случае поступательного и
вращательного движений), но и потенциальная, причем
средние значения кинетической и потенциальной энергий одинаковы.
i = iпост + iвращ + 2iколеб
Закон равномерного распределения энергии по степеням
свободы молекул не выполняется для газов при низких
температурах, т.к. при этом действуют не законы классической физики, а законы квантовой физики.
12.
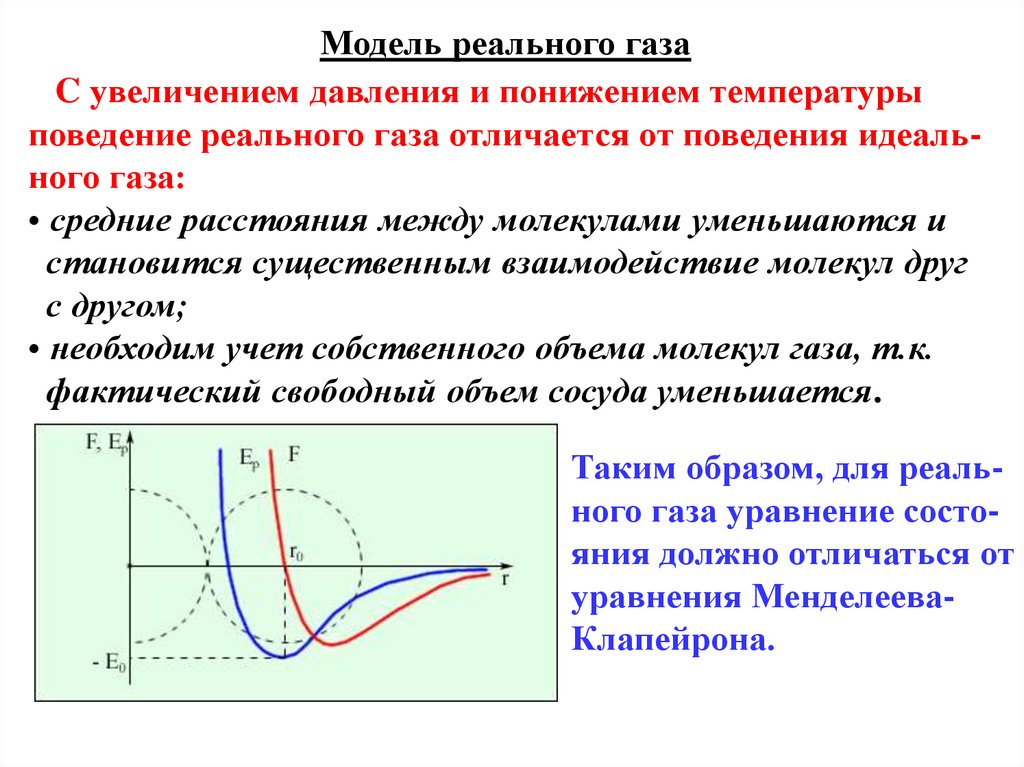
Модель реального газаC увеличением давления и понижением температуры
поведение реального газа отличается от поведения идеального газа:
• средние расстояния между молекулами уменьшаются и
становится существенным взаимодействие молекул друг
с другом;
• необходим учет собственного объема молекул газа, т.к.
фактический свободный объем сосуда уменьшается.
Таким образом, для реального газа уравнение состояния должно отличаться от
уравнения МенделееваКлапейрона.
13.
Уравнение Ван-дер-Ваальсадля произвольной массы реального газа
a
2
p 2 V b RT
V
Ян Ван-дер-Ваальс
(1837 – 1923)
При а = b = 0 уравнение Ван-дер-Ваальса
превращается в уравнение Менделеева-Клапейрона.
Азот при Т = 273 К
р, атм
1
100
200
500
рV
RT
1,000
0,994
1,048
1,390
(p
a
2
V
2
)(V b)
RT
1,000
1,000
1,009
1,014
14.
Изотермы Ван-дер-ВаальсаИзотермы Ван-дер-Ваальса – это кривые, дающие зависимость р = р(V) при заданных температурах Т в соответствии
с уравнением Ван-дер-Ваальса.
p
T
K
Tкр
T
p
p2
p
p1
Начиная с определённой для
каждого вещества температуры Tкр, при любом давлении вещественным оказывается только одно решение.
Температура Tкр называется критической.
T
Например: для водорода
Tкр = 33 К.
V1 V2 V3
V













 Физика
Физика








