Понятие функции. Свойства функций

1.

Лекция 1
Понятие функции
Свойства функций
Лекцию подготовила:
Фазлеева Эльмира Илдаровна,
канд. пед. наук, доцент
кафедры теории и технологий преподавания
математики и информатики ИМиМ

2.

Определение функции
Определение. Пусть каждому числу х из множества
чисел Х в силу некоторого (вполне определенного) закона
поставлено в соответствие единственное число у. Тогда
говорят, что у есть функция от х, определенная на
множестве Х и записывают у=f(х) или у(х).
Или, другими словами:
Если каждому значению х из некоторого множества
поставлено в соответствие по определенному правилу
единственное число у, то говорят, что на этом
множестве задана функция от переменной х, и
записывают у = f (x) или f(x). При этом х называют
независимой переменной или аргументом функции, а
у – зависимой переменной или функцией от х.

3.

Область определения, множество значений
функции
Определение. Множество значений х
(множество Х), для которых определены значения
у(х), называют областью определения функции у=f(х)
и обозначают D(y) или D(f).
Определение. Множество значений,
принимаемых переменной у (множество всех
значений зависимой переменной у) называют
множеством значений (областью значений) или
областью изменения функции у=f(x) и обозначают
Е(у) или E(f).

4.

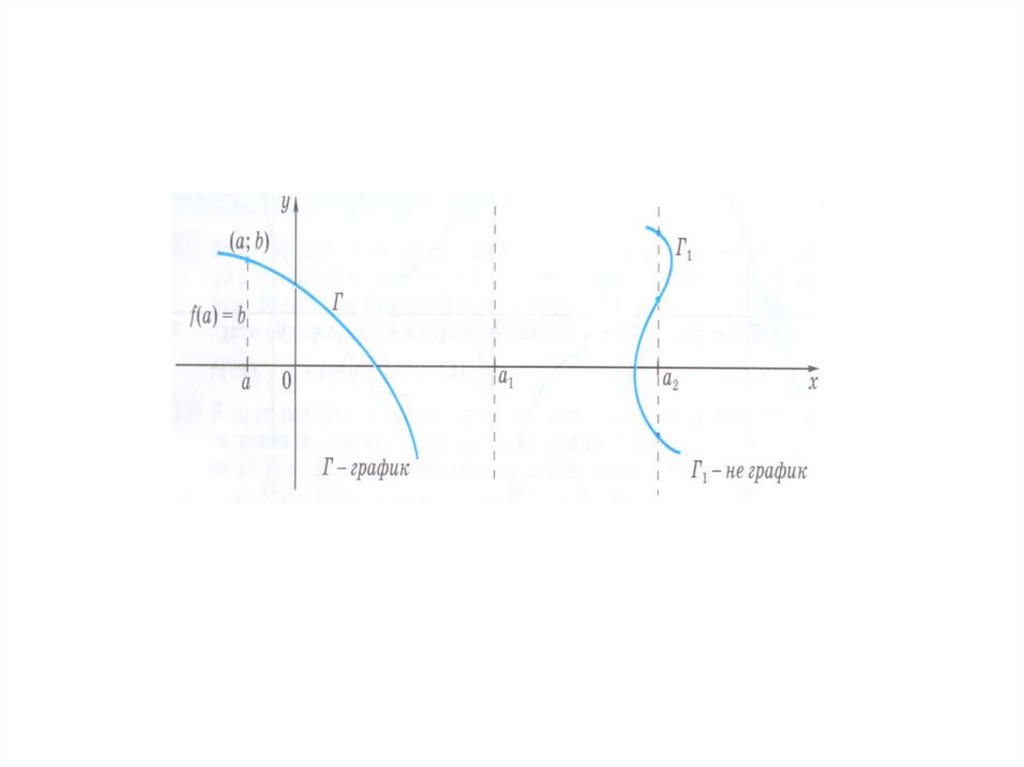
График функции
Определение. Графиком функции у=f(х)
называют множество всех точек координатной
плоскости хОу вида (х; f(x)), где х – любое число из
области определения функции.
Или, другими словами
Графиком функции называется
геометрическое место точек (ГМТ) плоскости, у
которых абсциссами служат значения независимой
переменной, а ординатами – соответствующие
значения функций, т.е. график – это ГМТ (x; f(x)).

5.

6.

Сложная функция
Определение. Пусть функция