Початкові та центральні моменти в теорії ймовірностей і математичній статистиці

1. Початкові та центральні моменти

2.

Узагальненими
числовими
характеристиками випадкових величин в
теорії ймовірностей і математичній
статистиці є початкові та центральні
моменти. Початковим моментом k-го
порядку випадкової величини X
називають математичне сподівання
величини Xk

3.

Коли
коли
і так далі.
Для дискретної випадкової
величини
початкові моменти визначають
залежністю

4.

для
неперервної інтегруванням
Якщо
неперервна величина задана
інтервалом
, то моменти
обчислюють за формулою

5.

Центральним
моментом k-го
порядку називається математичне
сподівання від

6.

Коли
для
маємо
при
при
і так далі.

7.

Для
дискретної випадкової величини
центральні моменти мають вигляд
для неперервної наступний

8.

Якщо
випадкова величина надежить
інтервалу
, то центральні моменти
визначають інтегруванням

9. Розглянемо приклад відшукання наведених величин.

Задано
функцію щільності ймовірностей
Обчислити
початкові та центральні
моменти другого та третього порядку
.

10.

Проміжні
операції при інтегруванні
пропущені, вони займають багато місця, а
Вам головне мати інструкцію для
обчислень так як приклади у Вас
будуть інші.
Для обчислення центральних
моментів інерції необхідно знати
математичне сподівання випадкової
величини, тому визначаємо його
першочергово

11.

Знайдене
математичне сподівання
підставляємо в формулу центральних
моментів. У випадку
отримаємо

12.

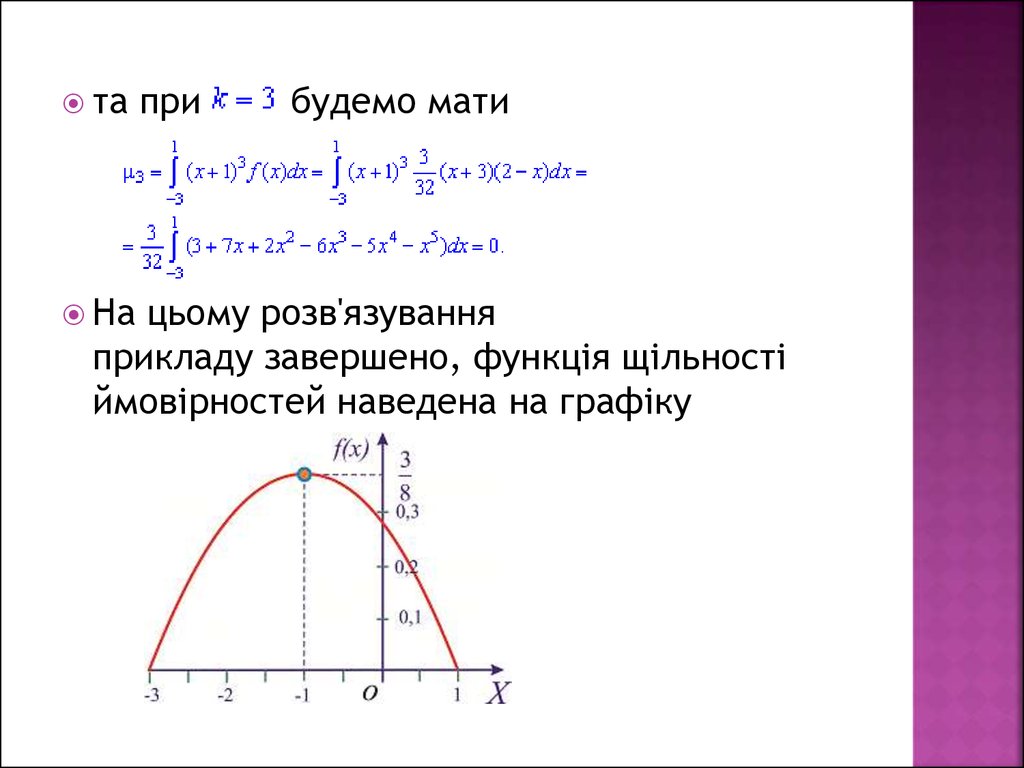
та
На
при
будемо мати
цьому розв'язування
прикладу завершено, функція щільності
ймовірностей наведена на графіку