Похожие презентации:
Випадкові величини
1. ВИПАДКОВІ ВЕЛИЧИНИ
Способи задання випадкових величин
Числові характеристики випадкових величин
Основні дискретні розподіли
Основні неперервні розподіли
Граничні теореми
1
2.
Означення. Випадковою величиною називаютьвеличину, яка в результаті випробування набуває
одне і тільки одне можливе значення, наперед не
відоме і не залежні від випадкових причин, які не
можуть бути враховані наперед.
Приклади.
1. Кількість хлопчиків , що народилися серед 100
новонароджених.
2. Відстань, яку пролетить снаряд при пострілі.
Дискретні і неперервні випадкові величини.
Випадкові величини: X, Y, Z,… , їх значення: x, y, z,…
2
3.
Означення.Законом
розподілу
дискретної
випадкової величини називають відповідність між
можливими значеннями і їх імовірностями.
Таблично:
X
p
x1
p1
x2 …
p2 …
xn
pn
p1+ p2 +…+ pn= 1
Аналітично:
Графічно:
p( xi ) f (i ), i 1, 2, ..., n
p1
x1
p2
x2
p3
p4
x3
x4
– багатокутник
розподілу
3
4.
p( X x)x1
x2
x
Означення. Функцією розподілу випадкової
величини Х називається функція F(x), що визначає
імовірність того, що випадкова величина Х
приймає значення, менше x, тобто
F(x) = p(X < x).
Функцію F(x) називають інтегральною функцією
розподілу.
Означення. Випадкова величина Х називається
неперервною, якщо її функція розподілу
неперервна на всій числовій осі.
4
5.
Властивості функції розподілу:1) 0 F ( x) 1
2) Якщо x1 < x2, то
F ( x1 ) F ( x 2 )
3) p(a x b) F (b) F (a)
4) Якщо можливі значення випадкової величини
x a
належать інтервалу (a, b), то а) F(x)=0 при
і б) F(x)=1 при x b
5) Якщо Х – непрерывна випадкова величина, то
імовірність того, що вона прийме одне визначене
значення дорівнює нулю: p(X=x) = 0.
5
6.
Означення. Щільністю розподілу імовірностейнеперервної випадкової величини Х називають
функцію, яка є похідною від функції розподілу:
f (x) = F’(x).
Функцію f(x) називають щільністю імовірності
або диференціальною функцією розподілу.
6
7.
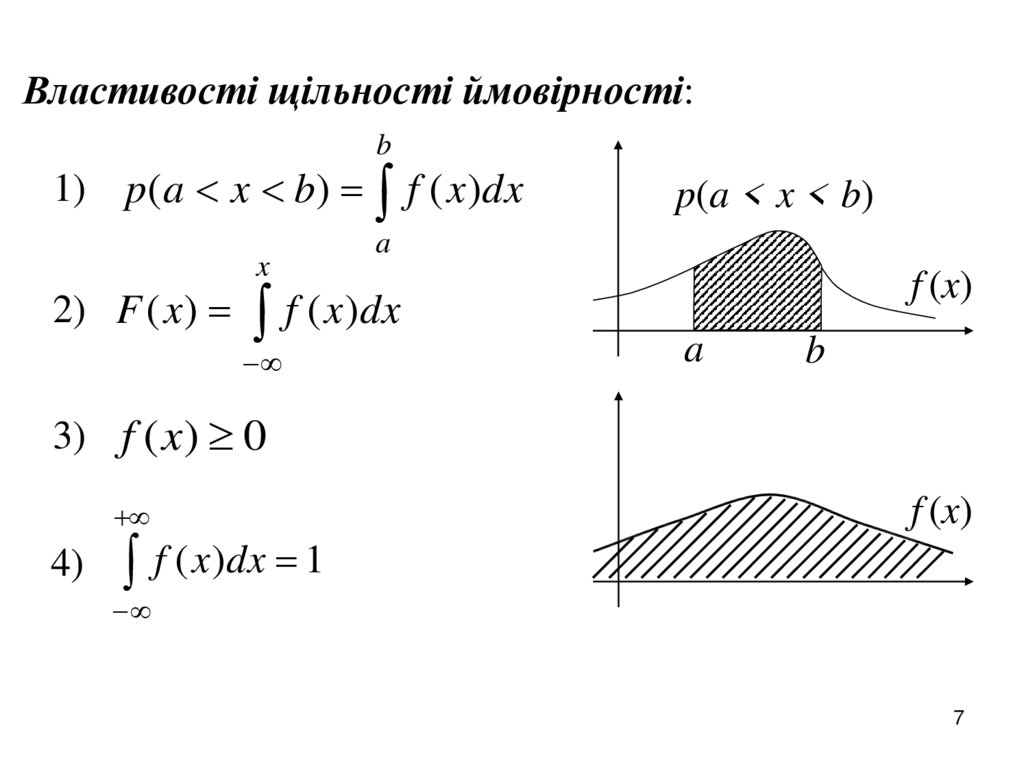
Властивості щільності ймовірності:b
1) p( a x b) f ( x )dx
2) F ( x )
x
a
f ( x)dx
p(a < x < b)
f (x)
a
b
3) f ( x) 0
4)
f ( x)dx 1
f (x)
7
8.
Дискретні і неперервні випадкові величини.Дискретна випадкова величина:
приймає окремі, ізольовані значення.
X
p
x1
p1
x2 …
p2 …
xn
pn
Неперервна випадкова величина:
можливі значення цілком заповнюють
проміжок.
F(x) = p(X < x)
функція
розподілу
f (x) = F’(x)
щільність
розподілу
деякій
9.
Означення. Математичне сподівання дискретноївипадкової величини Х називається сума добутків
всіх можливих значень випадкової величина на
відповідні їм імовірності. Позначається М (X).
Нехай
X
p
x1
p1
x2 …
p2 …
xn
pn
M ( X ) x1 p1 x2 p2 xn pn
Якщо випадкова величина Х приймає нескінченну
множину значень, то
M (X )
x
i 1
i
pi
9
10.
Імовірнісний зміст математичного сподівання:математичне
сподівання
наближено
дорівнює
середньому арифметичному значень випадкової
величини.
Доведення
Нехай n – кількість випробувань (достатньо велика).
Нехай випадкова величина Х приймає значення x1 , x2 , , xk
відповідно m1 , m2 , , mk раз.
m1 m2 mk n
Знайдем середнє арифметичне всіх значень:
x1m1 x2 m2 xk mk x m1 x m2 x mk
X
1
2
k
n
n
n
n
x1 p1 x2 p2 xk pk M ( X )
10
11.
Означення. Математичне сподівання неперервноївипадкової величини x, можливі значення, якої
належать відрізку [а, b], називається визначений
інтеграл
b
M ( X ) xf ( x)dx
a
Якщо можливі значення випадкової величини
розподілені по всій осі ОХ, то
M(X )
xf ( x)dx
11
12. Властивості математичного сподівання
• 1.• 2.
• 3.
Властивості математичного
сподівання
M ( C ) C, де C const.
M ( CX ) CM ( X )
n
n
M Xi M Xi
i 1 i 1
M ( aX b ) aM ( X ) b
M ( XY ) M ( X )M ( Y ) - тільки для
• 4.
• 5.
незалежних ВВ !
• 6. M ( X ) 0, якщо
f ( x ) f ( x )
13.
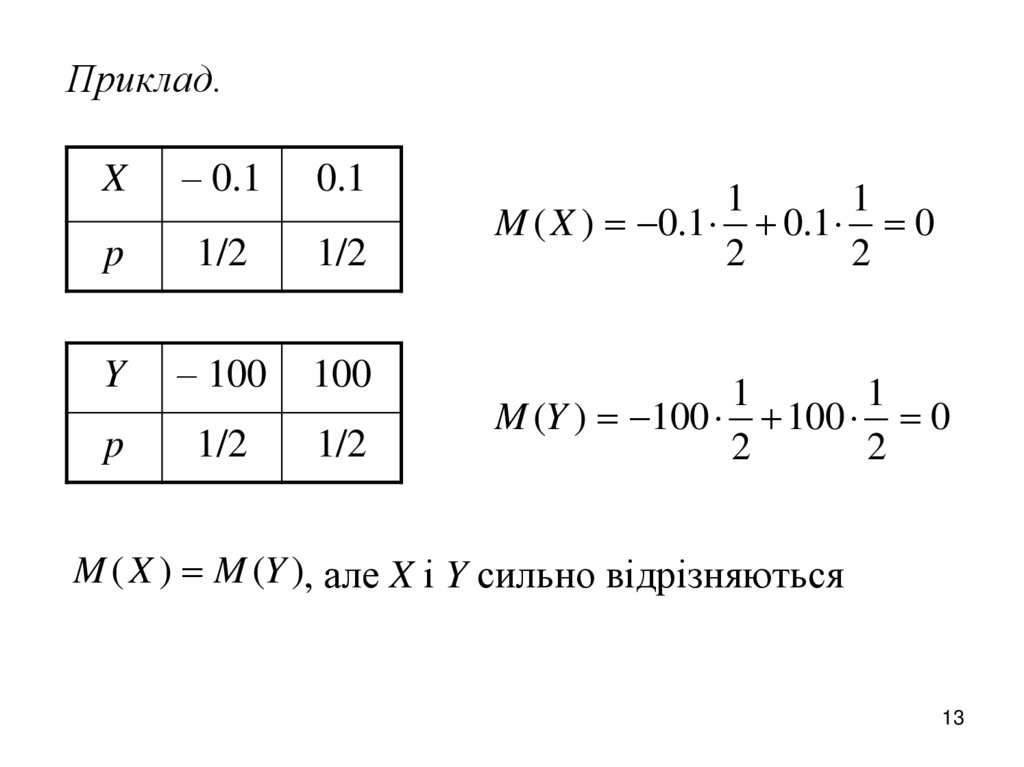
Приклад.X
– 0.1
0.1
p
1/2
1/2
Y
– 100
100
p
1/2
1/2
1
1
M ( X ) 0.1 0.1 0
2
2
1
1
M (Y ) 100 100 0
2
2
M ( X ) M (Y ), але X і Y сильно відрізняються
13
14.
Питання: чи можна оцінити дисперсії можливихзначень випадкової величини розрахувавши відхилення
кожного з цих значень від математичного сподівання і
потім знайти їх середнє?
X–М(Х) x1–М(Х) x2–М(Х)
p
p1
p2
…
xn–М(Х)
…
pn
M ( X M ( X ))
( x1 M ( X )) p1 ( x2 M ( X )) p2 ( xn M ( X )) pn
x1 p1 x2 p2 xn pn M ( X ) ( p1 p2 pn )
M (X )
1
M(X ) M(X ) 0
14
15.
(X–М(Х))2(x1–М(Х))2
(x2–М(Х))2
…
(xn–М(Х))2
p
p1
p2
…
pn
Означення. Дисперсією випадкової величини Х
називається математичне сподівання квадрата
відхилення
випадкової
величини
Х
від
математичного сподівання:
D( X ) M [ X M ( X )]2
15
16.
1. Дискретна випадкова величинаD( X ) M [ X M ( X )]
2
(X–М(Х))2
(x1–М(Х))2
(x2–М(Х))2
…
(xn–М(Х))2
p
p1
p2
…
pn
D( X ) ( x1 M ( X )) 2 p1 ( x 2 M ( X )) 2 p2
( x n M ( X )) pn
2
або
D( X ) ( xi M ( X )) 2 pi
i
D( X ) M ( X 2 ) [ M ( X )]2
16
17.
2. Неперервна випадкова величинаЗа означенням
D( X ) M [ X M ( X )]2
b
Але M ( X ) xf ( x )dx
a
b
2
(
x
M
(
X
))
f ( x )dx
M [ X M ( X )]
2
a
b
D( X ) ( x M ( X )) 2 f ( x )dx
a
b
D( X ) x 2 f ( x )dx [ M ( X )]2
a
17
18.
Середнє квадратичне відхиленняОзначення. Середнім квадратичним відхиленням
випадкової величини Х називається корінь з її
дисперсії:
( X ) D( X )
18
19. Властивості
Середнє квадратичне відхиленняДисперсія
1.
, де
2. D( C X ) D( X )
2
D
(
CX
)
C
D( X )
3.
n
n
4. D X i D X i
D( C ) 0
i 1
C const.
i 1
1. (С ) 0 , де C const.
2. ( C X ) ( X )
3. (СХ ) С ( Х )
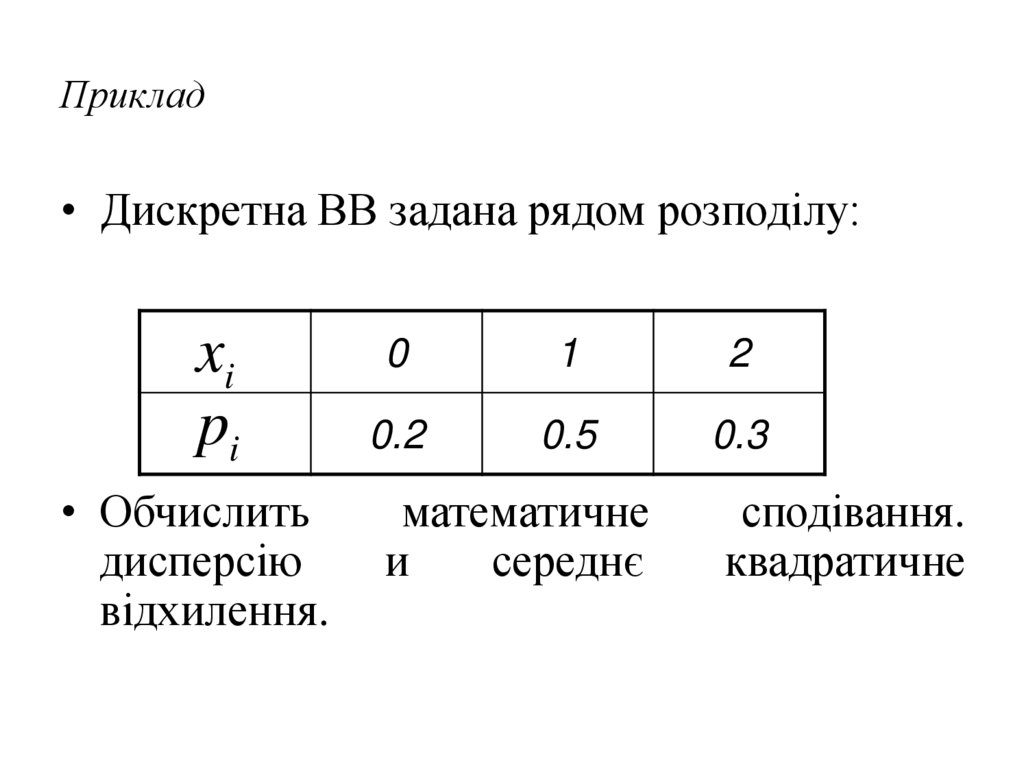
20. Приклад
• Дискретна ВВ задана рядом розподілу:xi
pi
• Обчислить
дисперсію
відхилення.
0
1
2
0.2
0.5
0.3
математичне
и
середнє
сподівання.
квадратичне
21.
n• 1. M ( X ) xi pi 0 0.2 1 0.5 2 0.3 1.1 .
i 1
• 2. D( X ) M ( X ) M ( X ) .
M( X 2 ) 0 2 0.2 12 0.5 2 2 0.3 1.7
.
D( X ) 1.7 ( 1.1)2 0.49
2
2
• 3. ( X ) D( X ) 0.49 0.7
.
.
22.
• Неперервнаімовірності
ВВ
задана
щільністю
2x при 0 x 1
f(x)
при x 0 и x 1
0
• Обчислить
дисперсію
відхилення.
математичне
и
середнє
сподівання.
квадратичне
23.
13 1
1
x
1. M ( x ) x f ( x )dx x 2xdx 2 x dx 2
3
0
0
2
0
2
3
2. D( X ) M ( X ) M ( X )
2
2
1
4 1
1
x
M ( x ) x f ( x )dx x 2xdx 2 x dx 2
4
0
0
2
1 2
D( X ) 0.28
2 3
2
2
2
3
3. ( X ) D( X ) 0.28 0.53
0
1
2
24.
4. Початковий момент порядку kk M (X )
k
k xik pi
– дискретна
i
k
k
x
f ( x)dx
– неперервна
Початковий момент першого порядку:
1 M ( X )
– математичне сподівання
25.
0 M (X 0) 1Якщо
k = 0, то
.
Якщо
k = 1, то
1 M ( X 1) М ( Х ) .
Якщо
k = 2, то
.
2 M (X 2)
математичне сподівання ВВ це початковий момент
1-го порядку, а дисперсія може бути виражена
через початкові моменти 1-го и 2-го порядків:
.
D( X ) M ( X ) [M ( X )] 2
2
2
2
1
26.
5. Центральний момент порядку kk M ( X M ( X )) k
k ( xi M ( X )) k pi
– дискретна
i
k ( x M ( X )) k f ( x)dx
– неперервна
Центральний момент другого порядку:
2 M ( X M ( X )) 2 – дисперсія
27.
• Якщо k = 0, то 0 M ( ) 1;• Якщо k = 1,то
1
1
1 M ( ) M X M ( X )
0
;
M( X ) M( X ) 0
• Якщо k = 2, то
2
2 M X M ( X ) D( X ) ,
• дисперсія ВВ це центральний момент
другого порядку : D( X ) 2
28.
• Вводиться коефіцієнт асиметрії(характеристика скошеності):
3
A 3 ,
x
• де – 3 3 3 2 1 2 13
• центральний момент 3-го порядку, а
середнє квадратичне відхилення ВВ
x
–
29.
• Центральний 4 3 4 3 1 6 2 12 3 14 момент4-го
порядку
використовується
для
характеристики положення вершини кривої
(крутості кривої) розподілу відносно
еталона – нормального розподілу, для якого
відношення
4
.
4
x
3
30.
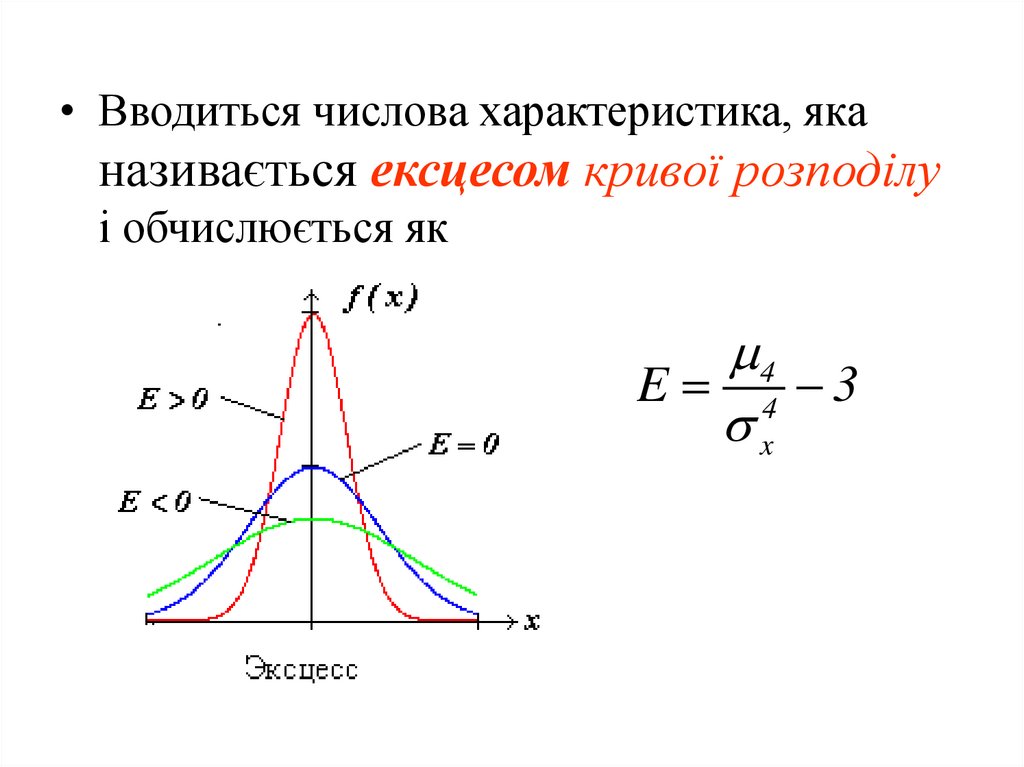
• Вводиться числова характеристика, яканазивається ексцесом кривої розподілу
і обчислюється як
4
E 4 3
x
31.
6. МодаДля дискретної випадкової величини мода – це
найбільш імовірне значення ВВ.
0,24 < 0,36 > 0,20
Мода: 20
32.
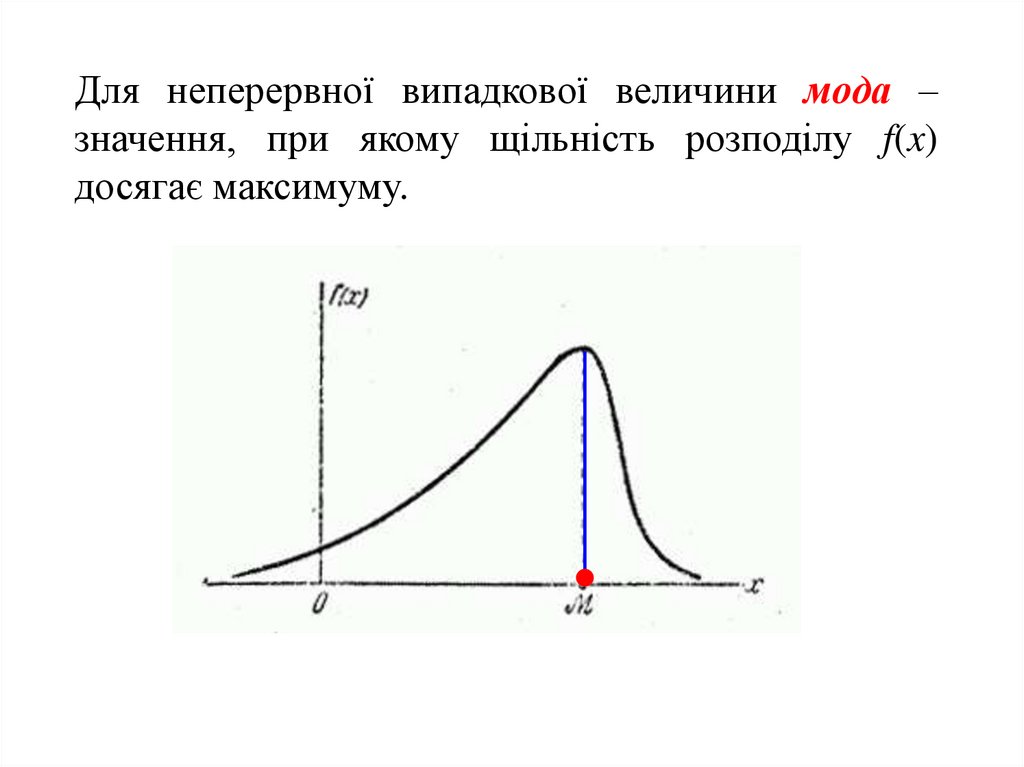
Для неперервної випадкової величини мода –значення, при якому щільність розподілу f(x)
досягає максимуму.
33.
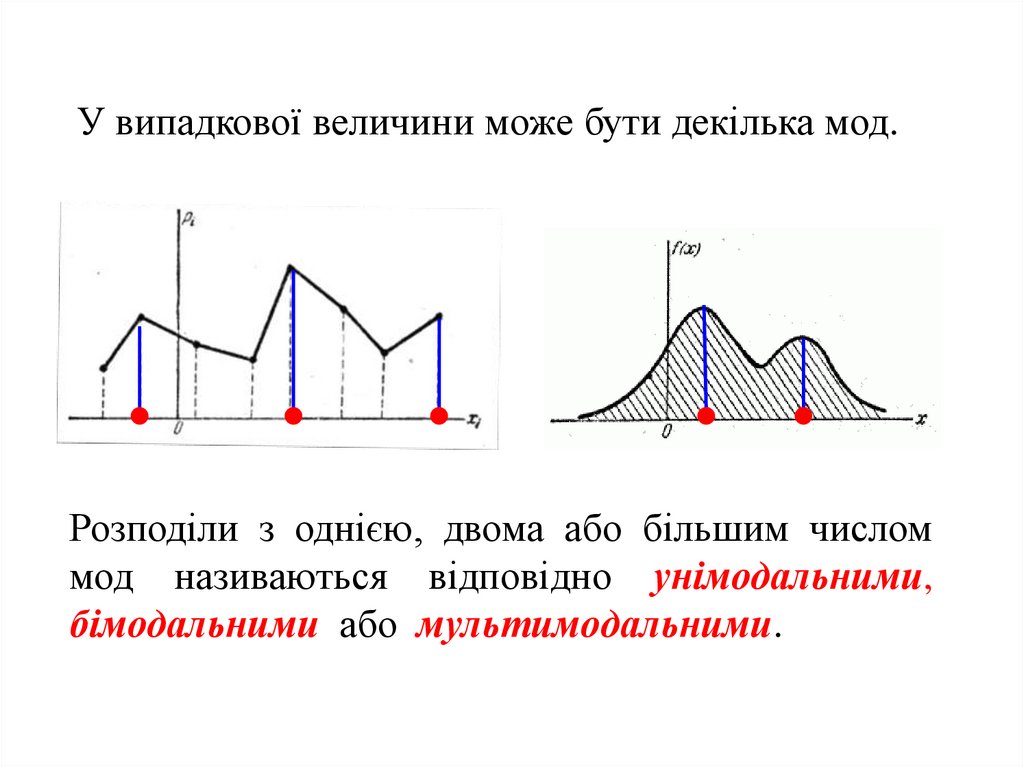
У випадкової величини може бути декілька мод.Розподіли з однією, двома або більшим числом
мод називаються відповідно унімодальними,
бімодальними або мультимодальними.
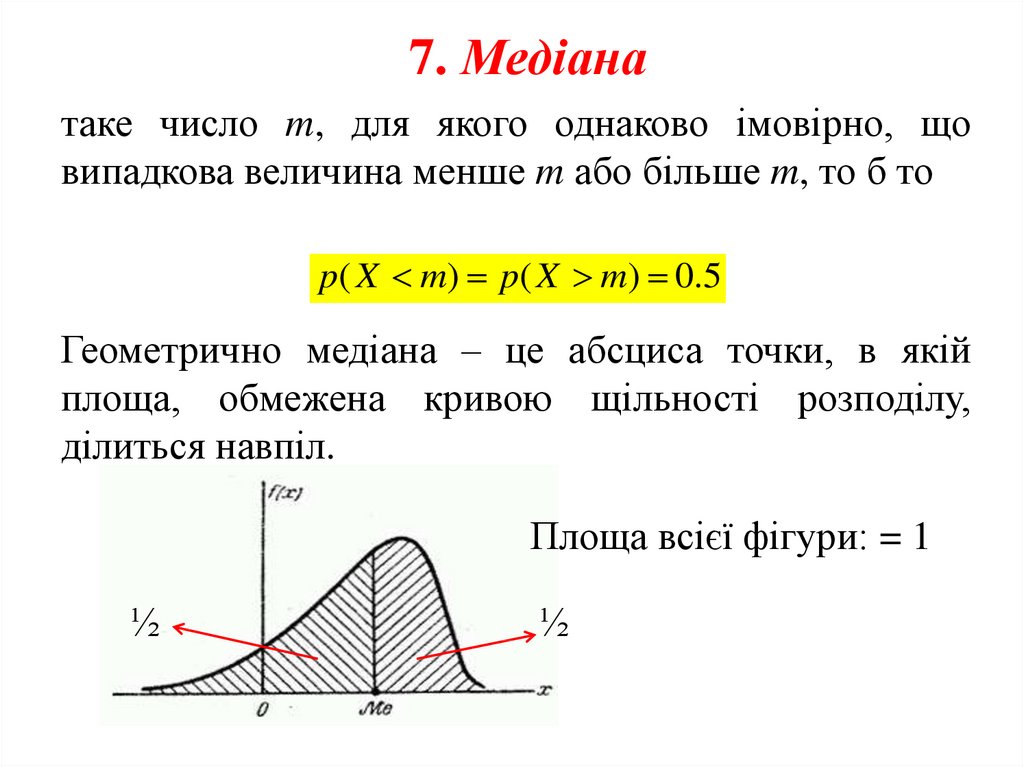
34.
7. Медіанатаке число m, для якого однаково імовірно, що
випадкова величина менше m або більше m, то б то
p( X m) p( X m) 0.5
Геометрично медіана – це абсциса точки, в якій
площа, обмежена кривою щільності розподілу,
ділиться навпіл.
Площа всієї фігури: = 1
½
½
35.
8. Квантіль рівня рp( X x p ) p F ( x p ) p
таке число хр, що
F(x) – функція розподілу
x p F 1 ( p )
F-1(x) – функція, обернена до функції розподілу
Квантіль рівня 0.5 – це медіана.
Квантілі рівня ¼, ½, ¾ називають відповідно
першим, другим і третім квартілями.
Квантілі рівня 0.1, 0.2, 0.3, …, 0.9 називають
децілями.
Квантілі рівня 0.01, 0.02, 0.03, …, 0.99 називають
процентілями.
36. Основні дискретні розподіли
Біноміальний розподіл
Розподіл Пуассона
Геометричний розподіл
Гіпергеометричний розподіл
Рівномірний розподіл
36
37.
1. Біноміальний розподілp – імовірність події А
Х – число появ події А в n незалежних випробуваннях
Можливі значення:
k = 0, 1, 2, …, n
q=1 – p.
p(k) = pkqn-kCnk
р – параметр розподілу
Біном Ньютона: ( p q)n
n
k k n k
C
np q
k 0
М(Х) = np
і
D(Х) = npq
37
38.
2. Розподіл Пуассонаn – дуже велике, p – дуже мале,
np
Х – число появ події А в n незалежних випробуваннях
Можливі значення:
p( k )
k = 0, 1, 2, …, n
k
e
k!
λ – параметр розподілу
M ( X ) D( X )
38
39.
3. Геометричний розподілp – імовірність події А
Х – число випробувань, яке необхідно провести до
першої появи події А
Можливі значення:
всі натуральні числа
k = 1, 2, 3, …
q=1 – p.
р – параметр розподілу
Р(k) = qk-1p
p, qp, q2p, q3p, q4p, ... – геометрична прогресія
q
M(X
M)( X )
p
q q
q
іD ( XD)( X )
p
p2 p2
39
40.
4. Гіпергеометричний розподілПартія з N виробів містить М стандартних.
З партії випадковим чином вибирають n виробів.
Х – число стандартних виробів серед відібраних
Можливі значення:
CMk C Nn kM
Р(k )
CNn
nn M
M
M
M((X
X ))
N
N
k = 0, 1, 2, …, min (M,n)
N, M, n – параметри розподілу
і
M
M ((N
N M
M )) ((N
N nn)) nn
D
D((XX ))
N
N 22 ((N
N 11))
40
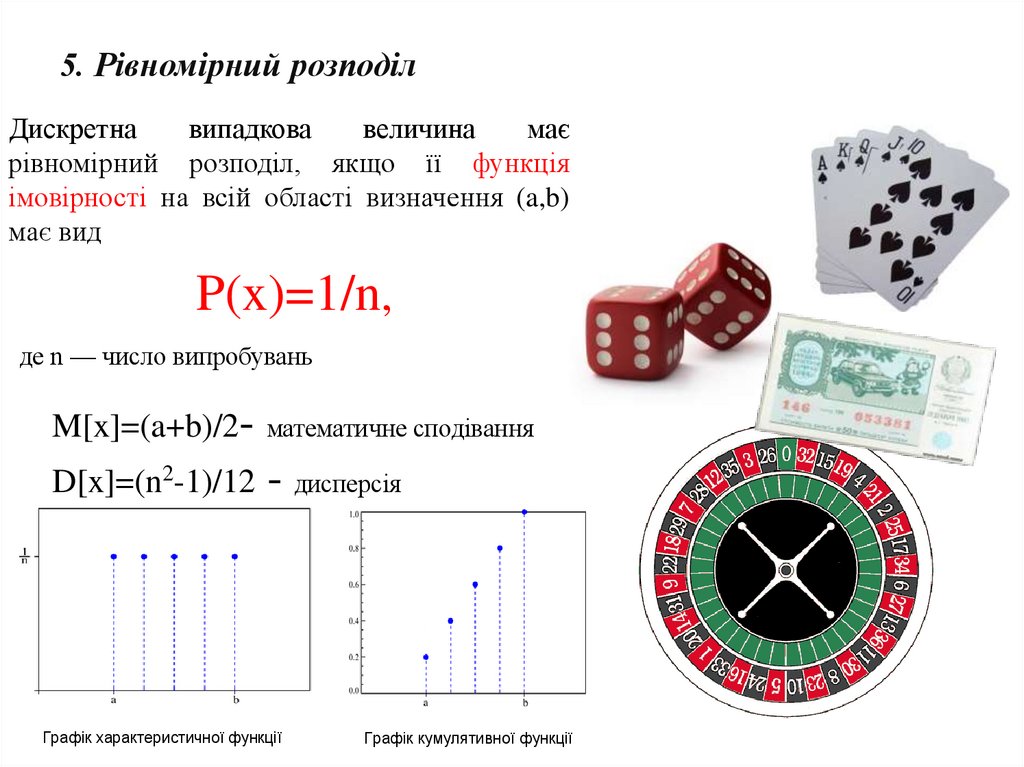
41. 5. Рівномірний розподіл
Дискретнавипадкова
величина
має
рівномірний розподіл, якщо її функція
імовірності на всій області визначення (a,b)
має вид
P(x)=1/n,
де n — число випробувань
M[x]=(a+b)/2-
математичне сподівання
D[x]=(n2-1)/12
- дисперсія
Графік характеристичної функції
Графік кумулятивної функції
42. Основні неперервні розподіли
• Рівномірний розподіл• Показниковий (експоненціальний)
розподіл
• Нормальний розподіл
• Розподіл Пірсона
• Розподіл Стьюдента
• Розподіл Фішера
42
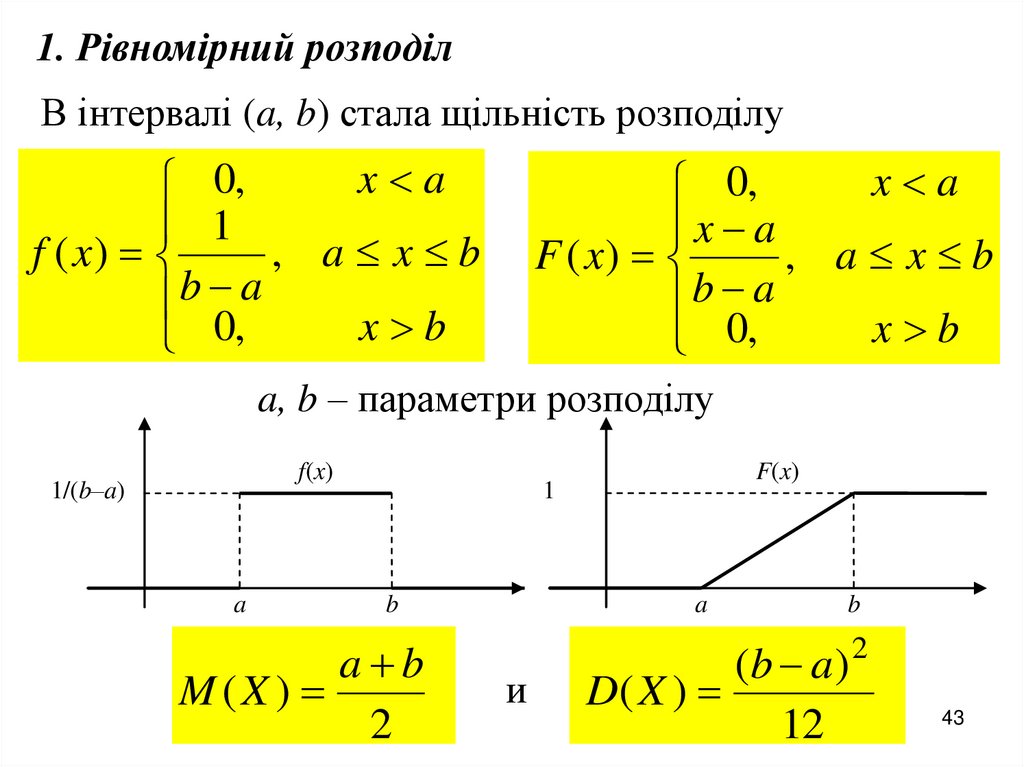
43.
1. Рівномірний розподілВ інтервалі (a, b) стала щільність розподілу
x a
0,
1
f ( x)
, a x b
b a
x b
0,
x a
0,
x a
F ( x)
, a x b
b a
x b
0,
a, b – параметри розподілу
f(x)
1/(b–a)
a
F(x)
1
b
a
b
a ba b
(b (ab) 2 a ) 2
иD( XD)( X )
M(X
M)( X )
12 12
2 2
43
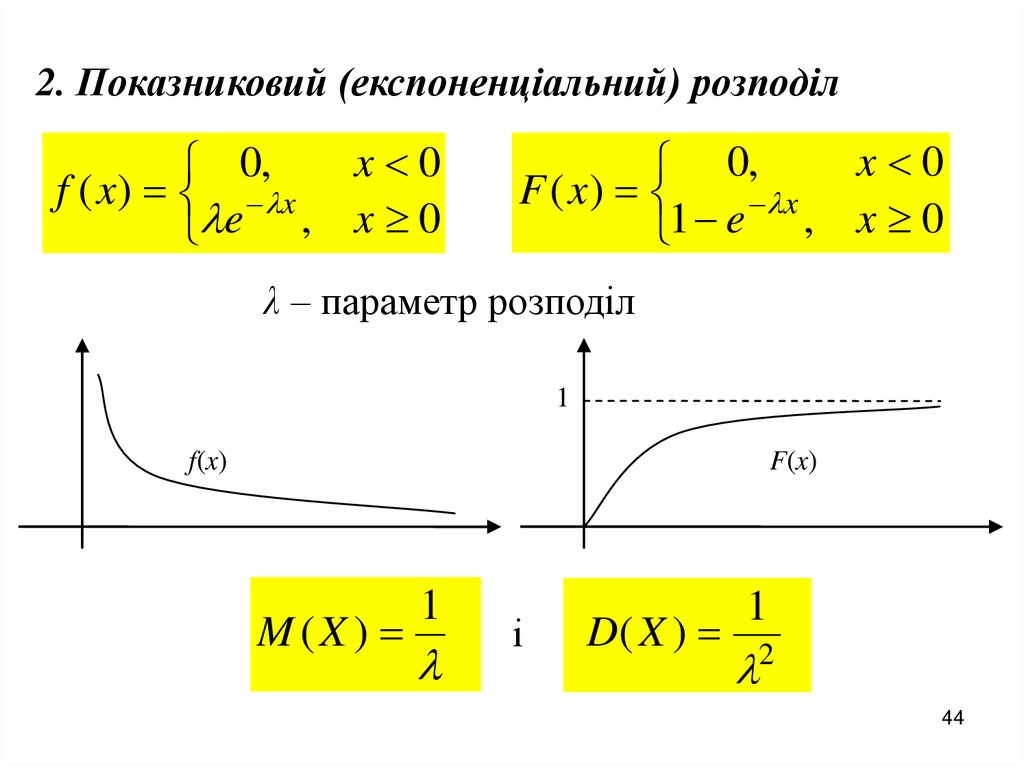
44.
2. Показниковий (експоненціальний) розподілx 0
0,
f ( x ) x
e , x 0
x 0
0,
F ( x)
x
1 e , x 0
λ – параметр розподіл
1
F(x)
f(x)
11
MM( X
( X) )
(X
( X) )
і DD
11
2 2
44
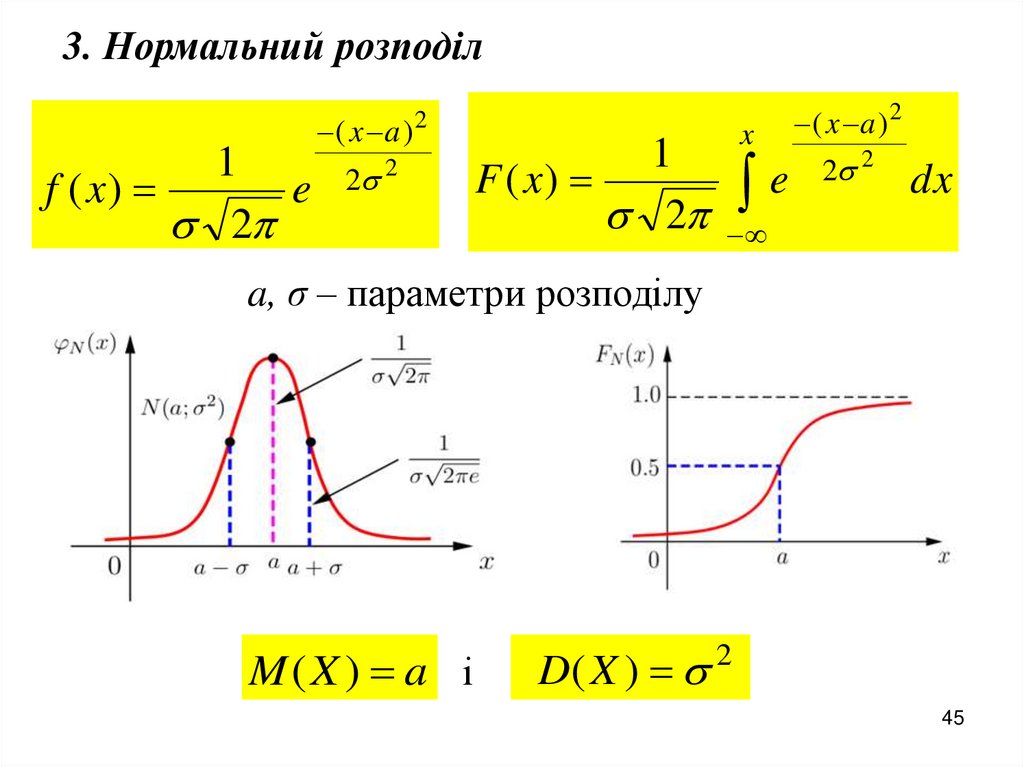
45.
3. Нормальний розподіл1
f ( x)
e
2
( x a )
2
2
2
1
F ( x)
2
x
e
( x a ) 2
2 2
dx
a, σ – параметри розподілу
(X
( X) )
MM( X
( X) ) aa і DD
22
45
46.
4647. Правило 3 сігм
При нормальному розподілі:M(+/-)σ=68,26%
M(+/-)2σ=95,44%
M(+/-)3σ=99,72%,
M(+/-)3σ - інтервал всіх можливих
значень
48. Властивості нормального розподілу
Правило 3 сігм (99,72% значень лежать в межахM+/-3σ)
Розподіл симетричний (А=0), ексцес Е = 0
Мода, медіана і математичне сподівання
співпадають
Значення, що лежать на однаковій відстані від
M(Х), будуть мати однакову імовірність
49.
24. Розподіл Пірсона ( -розподіл)
Нехай незалежні випадкові величини Х1, Х2, …, Хk
мають нормальний розподіл, до того ж матаматичне
сподівання кожної з них дорівнює 0, а середнє
квадратичне відхилення дорівнює 1.
Тоді сума квадратів цих величин:
2
2
X1
2
X2
2
Xk
k – параметр розподілу
має 2 – розподіл з k ступенями свободи.
1) випадкова величина χ2 ≥ 0.
2) при збільшення числа ступенів свободи розподіл
Пірсона повільно наближається до нормального.
49
50.
5. Розподіл Стьюдента (t-розподіл)Нехай X і Y – незалежні випадкові величини.
X має нормальний розподіл з математичним
сподіванням, що дорівнює 0, і середнім квадратичним
відхиленням, що дорівнює 1.
2
Y має – розподіл з k ступенями свободи.
Тоді величина
X
T
Y /k
має розподіл Стьюдента з k ступенями свободи
k – параметр розподілу
При збільшенні числа ступенів свободи розподіл
Стьюдента швидко наближається до нормального. 50
51.
6. Розподіл Фішера (F-розподіл)Нехай X і Y – незалежні випадкові величини.
X має – розподіл з k1 ступенями свободи.
2
Y має – розподіл з k2 ступенями свободи.
2
Тоді величина
X / k1
F
Y / k2
має розподіл Фішера з k1 і k2 ступенями свободи.
k1 і k2 – параметри розподілу
Оскільки X ≥ 0 і Y ≥ 0, то F ≥ 0.
51
52.
Граничні теореми1. Закон великих чисел.
2. Центральна гранична теорема.
52
53.
Теорема Чебишева. Якщо дисперсії незалежнихвипадкових величин
X1, X2,…, Xn,… не
перевищують сталого числа С, то для довільного
скільки завгодно малого числа > 0 справедлива
рівність
n
1 n
1
lim p X i M ( X i ) 1
n
n
i 1
n i 1
Наслідок з теореми Чебишева. Якщо випадкові
величини X1, X2,…, Xn,… незалежні і однаково
розподілені, з математичним сподіванням a і
2
дисперсією
, то для довільного скольки завгодно
малого числа > 0 справедлива рівність
1 n
lim p X i a 1
n n
i 1
53
54.
Теорема Бернуллі. Якщо в кожному з n незалежнихвипробуваннях імовірність p того, що відбудеться
подія A стала, то для довільного, скільки завгодно
малого числа > 0 справедлива рівність
m
lim p p 1,
n n
де m – число появ події A в n випробуваннях.
54
55.
Теорема Ляпунова. Якщо випадкова величина Xдорівнює сумі великої кількість взаємнонезалежних
випадкових величин, усі значення якої мають
скінченні математичні сподівання і дисперсії, і
жодне із значень різко не відрізняється від всіх
інших, тобто має незначний вплив на їх суму, то X
має розподіл, який близький до нормального.
55
56.
Теорема. Нехай незалежні випадкові величины X1,X2,…, Xn однаково розподілені з математичним
сподіванням a і середнім квадратичним відхиленням .
Тоді випадкова величина
1 n
Xi
n i 1
має
розподіл,
близький
до
нормального
з
математичним сподіванням, що дорівнює a і середнім
квадратичним відхиленням / n
56
57.
Наслідок. Нехай незалежні випадкові величины X1,X2,…, Xn однаково розподілені з математичним
сподіванням a і середнім квадратичним відхиленням .
Тоді випадкова величина
1 n
Xi a
n i 1
/ n
має
розподіл,
близький
до
нормального
з
математичним сподіванням, що дорівнює 0, і середнім
квадратичним відхиленням, рівним 1.
57

















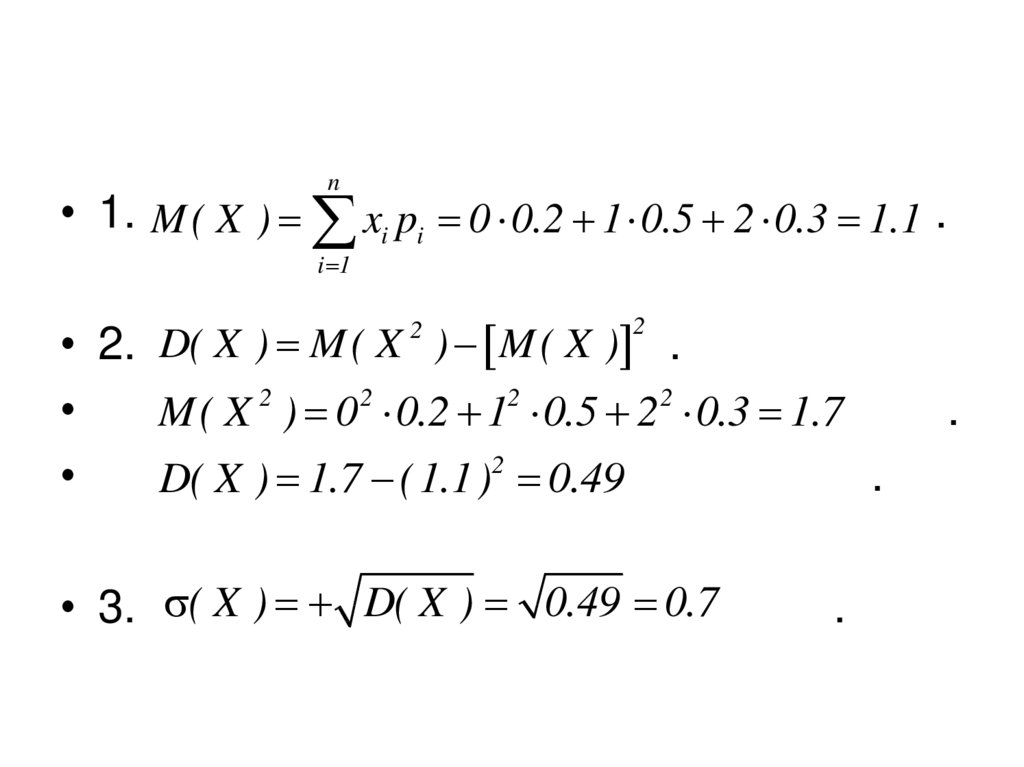

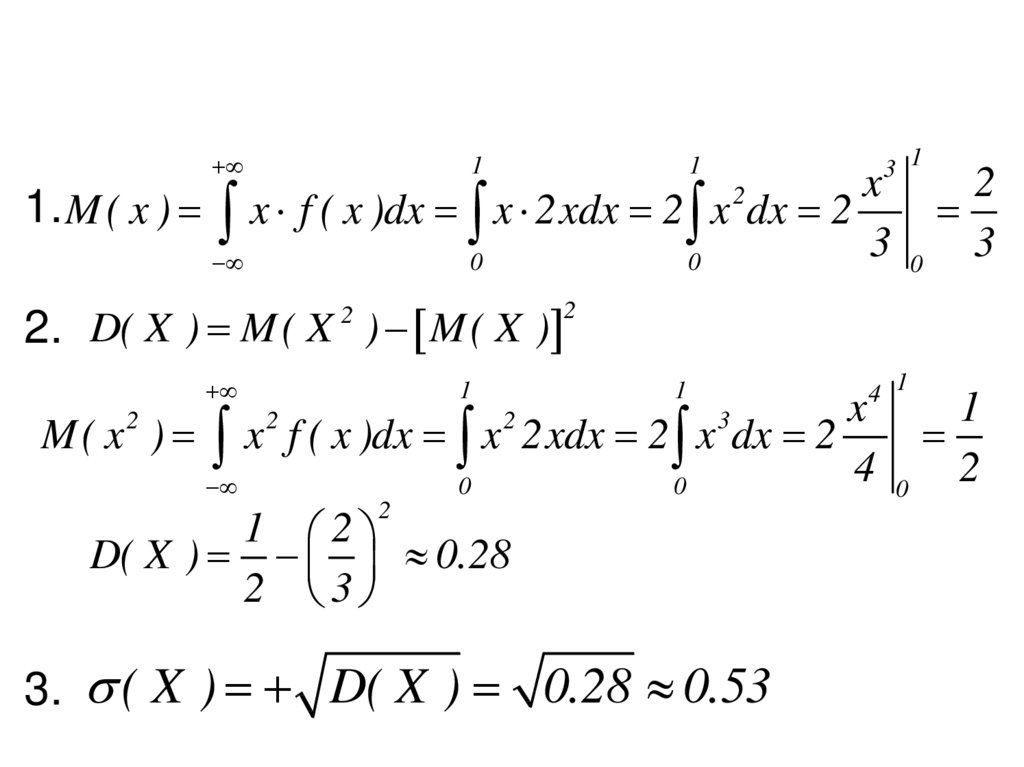


























 Математика
Математика








