Похожие презентации:
Випадкові величини та їх числові характеристики. Закони розподілу випадкових величин
1.
Тема 4:“Випадкові величини та їх числові характеристики.
Закони розподілу випадкових величин ”
2.
ЗАВДАННЯ1. Кожна з літер слова «інтеграл» записана на окремому
аркуші папері, які перемішані в довільному порядку.
Визначити ймовірність складання слова «гра» при
витягуванні 3-х аркушів в порядку їх появи.
2.Ймовірність, що потрібна студенту сума грошей є у його
трьох друзів становить 0,6 0,8 0,9. Знайти ймовірність
того, що хоч один друг позичить необхідну суму.
2
3.
МАТЕМАТИЧНІ МЕТОДИ У ПСИХОЛОГІЇ3
Тема 4. „Випадкові величини та їх числові
характеристики. Закони розподілу випадкових
величин”
Заняття 3а. „ Розрахунок числових характеристик
випадкових величин ”.
Навчальні питання:
1. Розрахунок числових характеристик випадкових величин.
2.Розрахунок середнього арифметичного, моди, медіани,
математичного сподівання та дисперсії.
Навчальна література:
- Іванюта І.Д., Рибалка В.І., Рудоміно-Дусятська І.А.. Елементи теорії
ймовірностей та математичної статистики.- Київ-2003,
стр 35-39.
- Барковський В.В., Барковська Н.В., Лопатін О.К. . Теорія ймовірностей
4.
4випадкова величина
випадкова величина - числова характеристика події, яка
може приймати лише одне числове значення,
заздалегідь невідоме і обумовлене випадковими
причинами.
неперервні
дискретні
5.
Ймовірність випадкових величин5
Дискретна випадкова величина може набувати лише
певних окремих значень із заданими ймовірностями
При киданні грального кубика імовірність розподіляється:
1
2
3
4
5
6
1\6
1\6
1\6
1\6
1\6
1\6
6.
6Ймовірність випадкових величин
Неперервна випадкова величина може набувати будь-яких
значень з певного інтервалу числової прямої чи
об’єднання інтервалів із заданими
ймовірностями.
1 1,1 1,12 1,1245
3
4
Розподіл випадкової величини - розподіл імовірностей
значень випадкової величини у відповідному імовірнісному
просторі.
7.
Закон розподілу випадкової величиниЗадається:
-
аналітично,
таблично;
графічно.
РЯД РОЗПОДІЛУ
Х
х1
х2
...
хn
Р(Х)
р1
р2
....
рn
7
8.
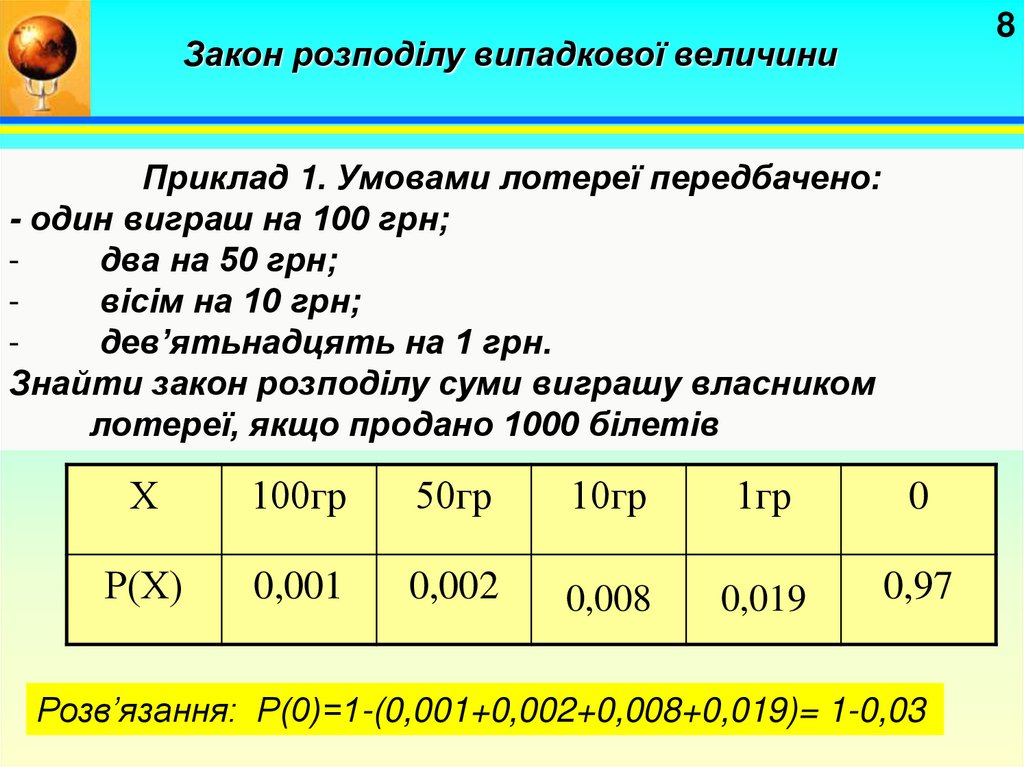
8Закон розподілу випадкової величини
Приклад 1. Умовами лотереї передбачено:
- один виграш на 100 грн;
два на 50 грн;
вісім на 10 грн;
дев’ятьнадцять на 1 грн.
Знайти закон розподілу суми виграшу власником
лотереї, якщо продано 1000 білетів
Х
100гр
50гр
10гр
1гр
0
Р(Х)
0,001
0,002
0,008
0,019
0,97
Розв’язання: Р(0)=1-(0,001+0,002+0,008+0,019)= 1-0,03
9.
Характеристики розподілу випадкової величини-
функція розподілу;
математичне сподівання,
дисперсія,
середньоквадратичне відхилення,
асиметрія,
ексцес,
квантилі
9
10.
Характеристики розподілу випадковоївеличини
Математичним сподіванням дискретно розподіленої випадкової
величини будемо називати суму добутків значень випадкової
величини на їх імовірності.
MX xk P X xk xk pk
k
k
Математичним сподіванням скалярної неперервно розподіленої випадкової
величини будемо називати інтеграл по всій дійсній осі від добутку випадкової
величини на її щільність розподілу.
MX xf x dx
10
11.
Характеристики розподілу випадковоївеличини
В багатьох практичних випадках важливим є питання про те,
наскільки великі відхилення випадкової величини від її математичного
сподівання. Для оцінки розсіювання значень випадкової величини в
околі її математичного сподівання вводиться нова числова
характеристика дисперсія (dispersion) (“дисперсія” розсіювання).
Дисперсія випадкової величини є математичне сподівання квадрата
відхилення випадкової величини від її математичного сподівання.
Дисперсія не може бути від’ємною.
Вона тим менша чисельно, чим тiсніше групуються значення х в
околі математичного сподівання М.
Навпаки, якщо можливі великі відхилення х від М і якщо це
відбувається з великими ймовірностями, то дисперсія також буде
великою.
Таким чином, дисперсію і середнє квадратичне можна розглядати як
міру розсіювання випадкової величини навколо середнього значення М.
11
12.
Характеристики розподілу випадкової величиниДисперсією дискретної випадкової величини
називається математичне сподівання квадрата
відхилення випадкової величини від свого
математичного сподівання.
DX xk MX pk
2
k
неперервно розподіленої
DX x MX f x dx
2
Величина X
DX називається середнім квадратичним
(або стандартним) відхиленням випадкової величини
Х.
12
13.
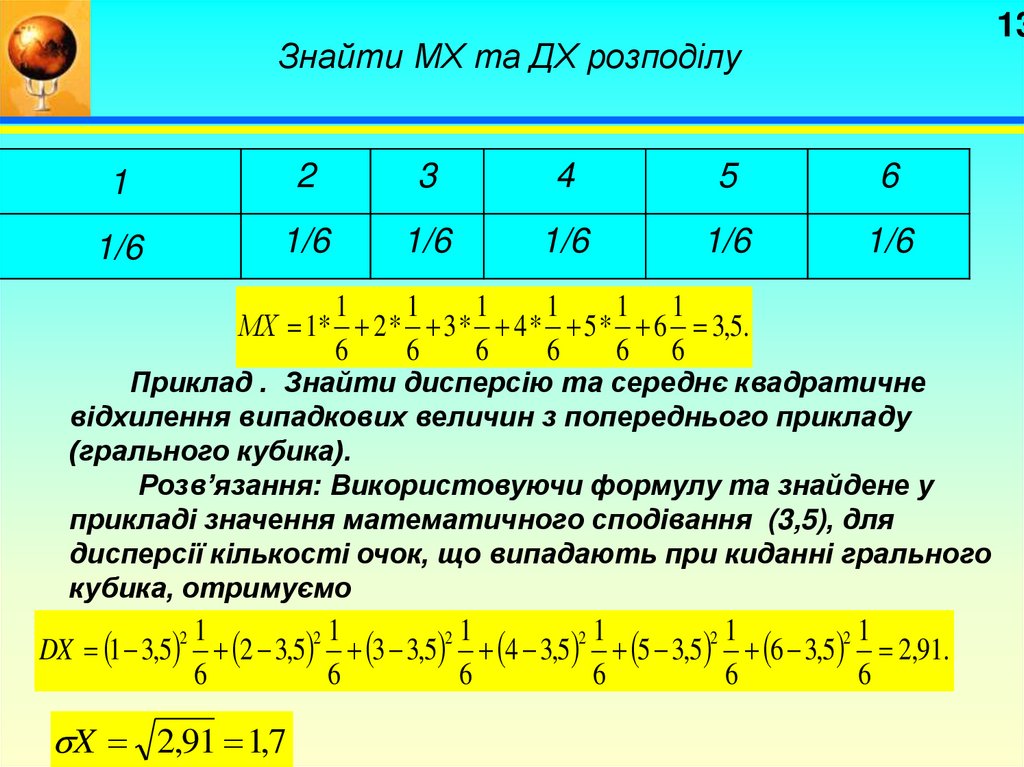
13Знайти МХ та ДХ розподілу
1
2
3
4
5
6
1/6
1/6
1/6
1/6
1/6
1/6
1
1
1
1
1 1
МX 1* 2 * 3 * 4 * 5 * 6 3,5.
6
6
6
6
6 6
Приклад . Знайти дисперсію та середнє квадратичне
відхилення випадкових величин з попереднього прикладу
(грального кубика).
Розв’язання: Використовуючи формулу та знайдене у
прикладі значення математичного сподівання (3,5), для
дисперсії кількості очок, що випадають при киданні грального
кубика, отримуємо
DX 1 3,5
2
1
21
21
21
21
21
2 3,5 3 3,5 4 3,5 5 3,5 6 3,5 2,91.
6
6
6
6
6
6
X 2,91 1,7
14.
14ЗАВДАННЯ:
Знайти МХ та ДХ розподілу, моду, медіану
Розподіл змінної та значення її ймовірності
Назва змінної та її
ймовірність
Х
3
5
7
8
9
(ймовірність)р
0,3
0,1
0,2
0,2
0,2
Н
1
3
5
7
9
(ймовірність)р
0,2
0,3
0,1
0,2
0,2
О
2
4
6
8
10
(ймовірність)р
0,3
0,3
0,1
0,1
0,2
І
1
2
3
4
5
(ймовірність)р
0,3
0,2
0,1
0,2
0,2
Т
3
4
5
6
7
(ймовірність)р
0,2
0,1
0,3
0,2
0,2
15.
Характеристики розподілу випадкової величиниПриклад 2. Знайти математичне сподівання
випадкової величини, якою є кількість очок, що
випадає при киданні грального кубика.
Розв’язання: Розподіл вказаної випадкової
величини має вигляд
Хі
1
2
3
4
5
6
Рі 1/6 1/6 1/6 1/6 1/6 1/6
Тому користуючись формулою знаходимо
1
1
1
1
1
1 21
MX 1 2 3 4 5 6
3,5
6
6
6
6
6
6 6
15
16.
Характеристики розподілу випадкової величиниДисперсія та стандартне відхилення
випадкової величини. Асиметрія і ексцес.
Дисперсією випадкової величини називається
математичне сподівання квадрата відхилення
випадкової величини від свого математичного
сподівання.
Отже, для обчислення дисперсії дискретно
розподіленої випадкової величини маємо формулу
DX xk MX pk
2
k
Величина X
DX називається середнім квадратичним
(або стандартним) відхиленням випадкової величини
Х.
16
17.
Характеристики розподілу випадковоївеличини
17
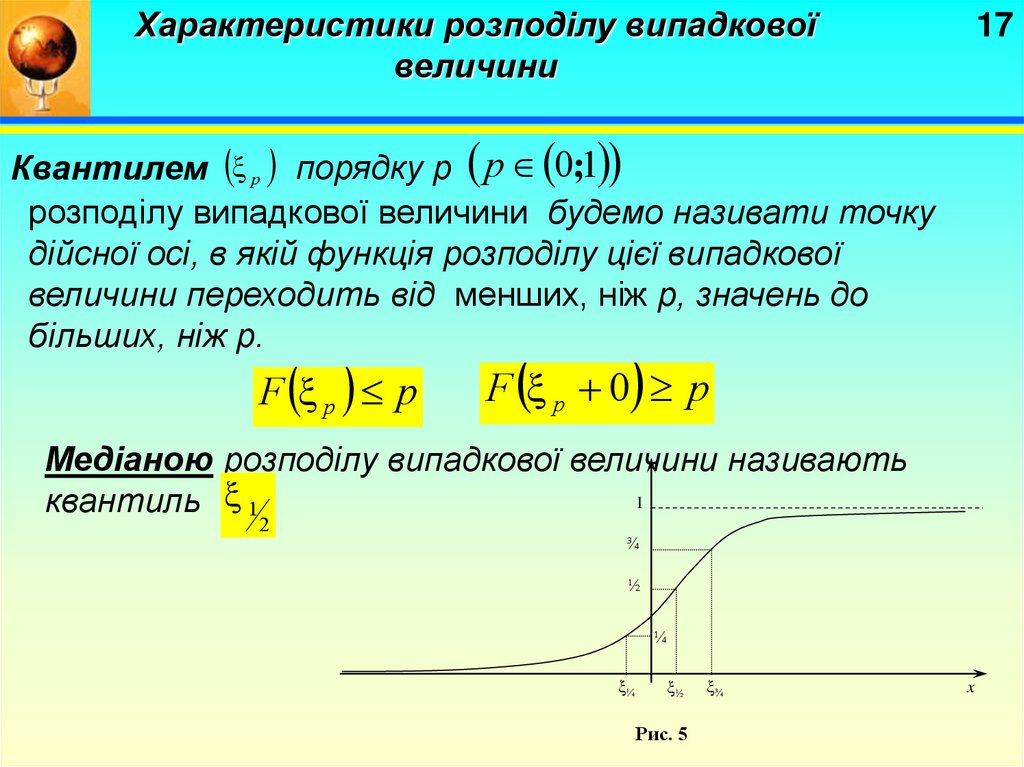
Квантилем p порядку р p 0;1
розподілу випадкової величини будемо називати точку
дійсної осі, в якій функція розподілу цієї випадкової
величини переходить від менших, ніж р, значень до
більших, ніж р.
F p p
F p 0 p
Медіаною розподілу випадкової величини називають
1
квантиль 1
2
¾
½
¼
ξ¼
ξ½
Рис. 5
ξ¾
x
18.
Характеристики розподілу випадковоївеличини
M X MX
3
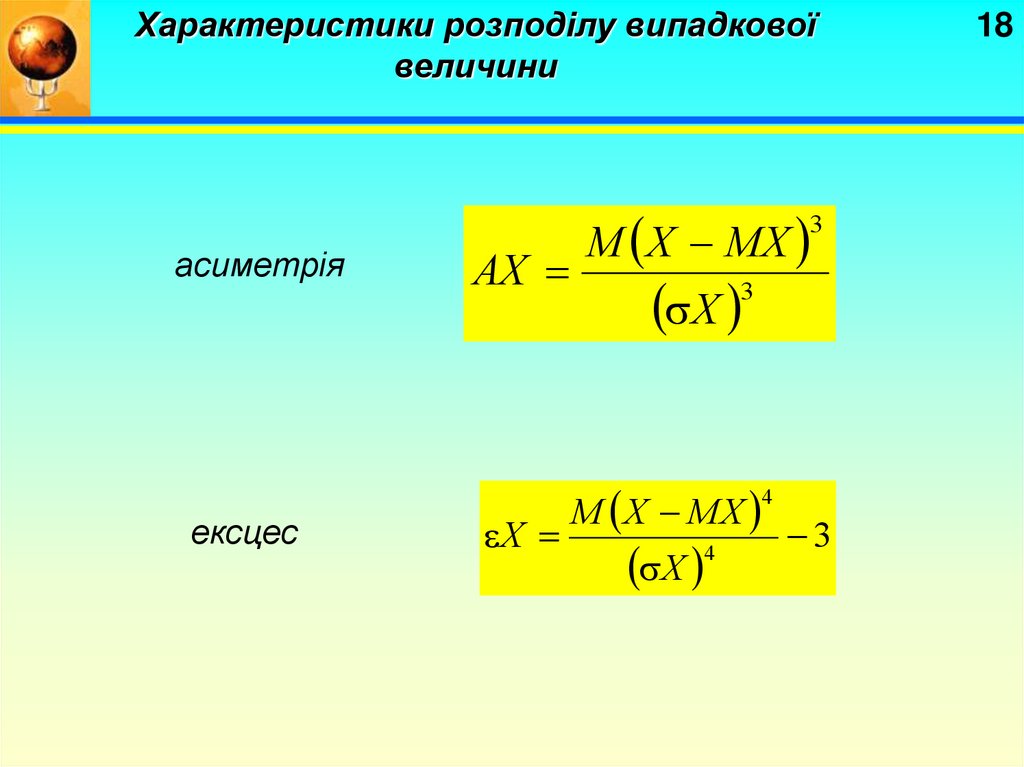
асиметрія
ексцес
AX
X
X
3
4
M X MX
3
4
X
18














 Математика
Математика








