Похожие презентации:
Произвольная плоская система сил
1.
ПРОИЗВОЛЬНАЯПЛОСКАЯ СИСТЕМА
СИЛ.
ЛЕКЦИЯ 3
mailto:esolodovnik@yandex.ru
Составитель: Солодовник Е.В.
кафедра Механики деформируемого твердого
тела
ТОГУ
2.
3.1. Приведение произвольнойплоской системы сил к
простейшему виду
3.
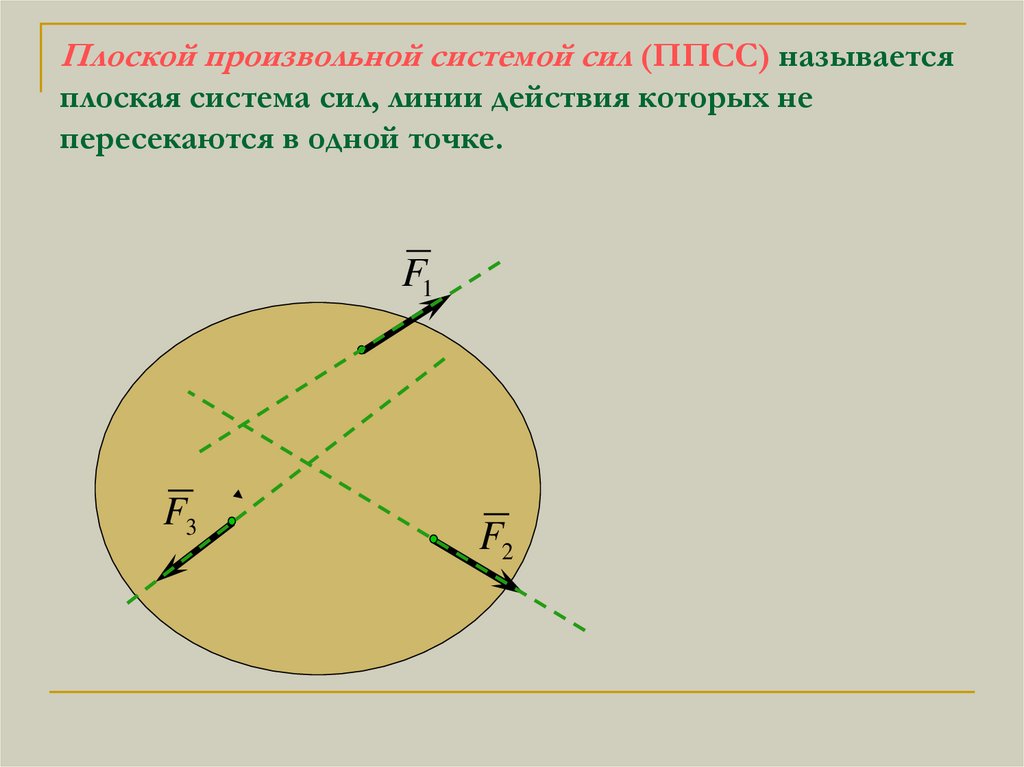
Плоской произвольной системой сил (ППСС) называетсяплоская система сил, линии действия которых не
пересекаются в одной точке.
F1
F3
F2
4.
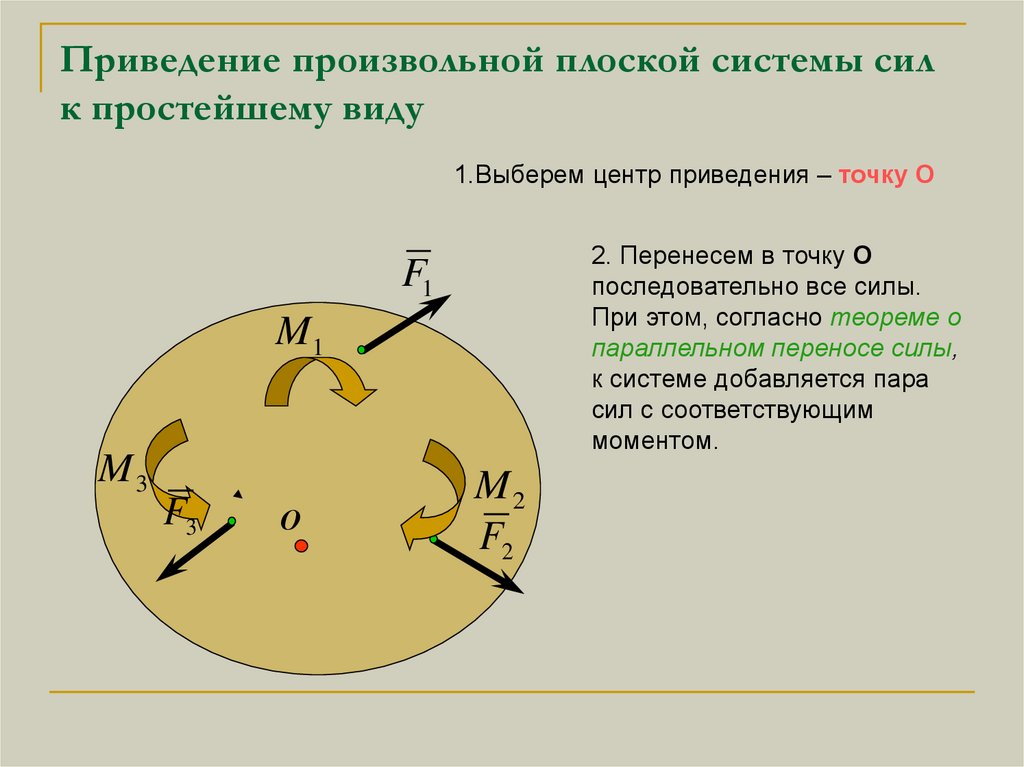
Приведение произвольной плоской системы силк простейшему виду
1.Выберем центр приведения – точку О
2. Перенесем в точку О
последовательно все силы.
При этом, согласно теореме о
параллельном переносе силы,
к системе добавляется пара
сил с соответствующим
моментом.
F1
M1
M3
F3
О
M2
F2
5.
Приведение произвольной плоской системы силк простейшему виду
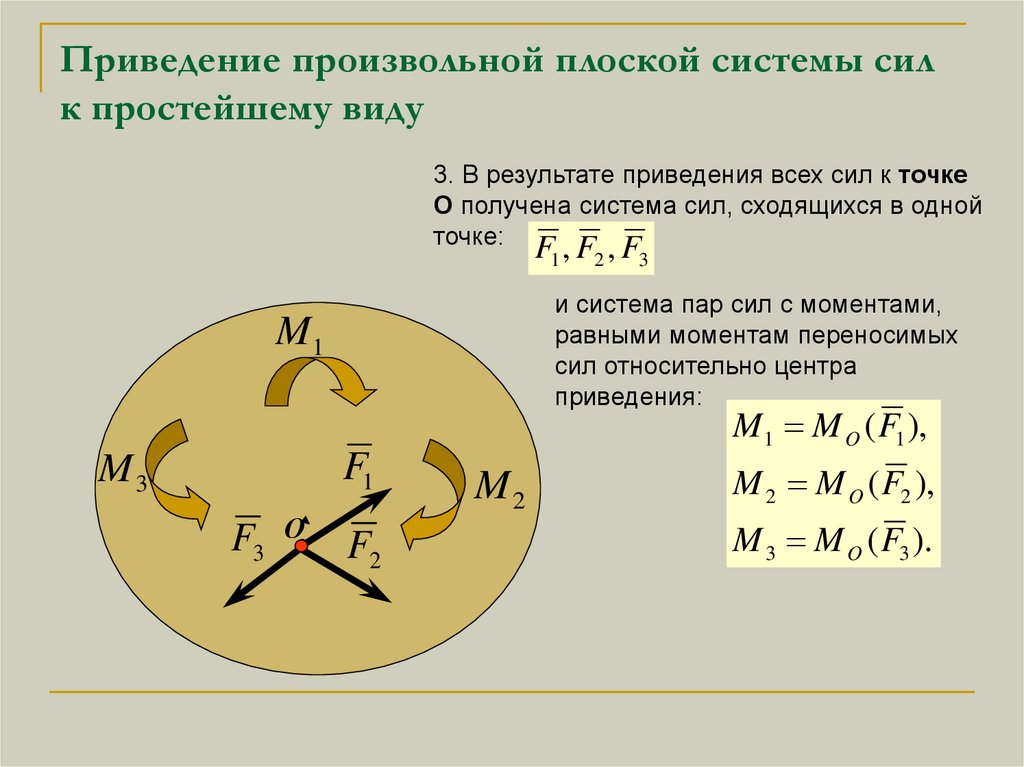
3. В результате приведения всех сил к точке
О получена система сил, сходящихся в одной
точке:
F1 , F2 , F3
и система пар сил с моментами,
равными моментам переносимых
сил относительно центра
приведения:
M1
M 1 M O ( F1 ),
F1
M3
F3
О
F2
M2
M 2 M O ( F2 ),
M 3 M O ( F3 ).
6.
Приведение произвольной плоской системы силк простейшему виду
4. Система сил, сходящихся в точке О
приводится к одной результирующей силе R0–
главному вектору всех сил, равному
геометрической сумме всех сил действующих
на тело:
R 0 Fk F1 F2 ... Fn
M1
MO
M3
F1
О
F3
F2
R0
M2
Моменты складываются и
приводятся к одному
результирующему моменту М0 главному моменту всех сил
M O M O ( Fi )
7.
Таким образом произвольная плоская система силприводится к главному вектору всех сил, равному
геометрической сумме всех сил действующих на
тело и к главному моменту всех сил, равному сумме
моментов всех действующих сил относительно
центра приведения.
MO
О
R0
8.
3.2. Условия равновесияпроизвольной плоской системы
сил
9.
Условия равновесия произвольнойплоской системы сил
Необходимым и достаточным условием
равновесия плоской системы сил являются
равенство нулю главного вектора всех сил
системы R0 и главного момента всех сил
системы М0
R Fk 0
0
и
M O M O ( Fi ) 0
10.
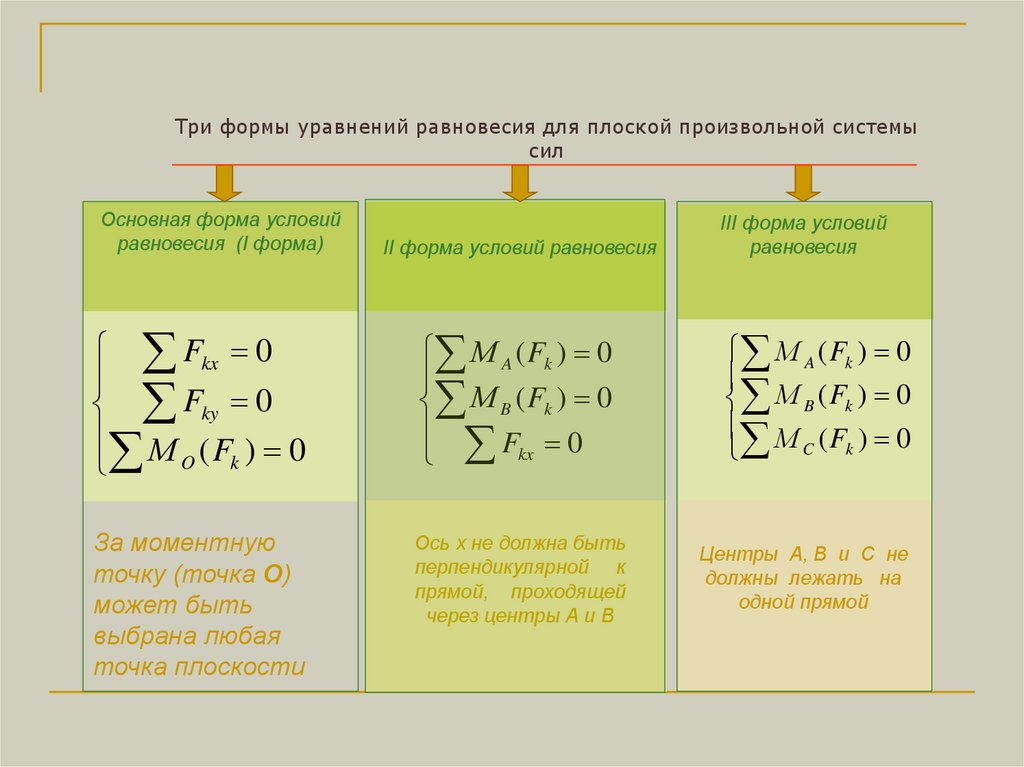
Три формы уравнений равновесия для плоской произвольной системысил
Основная форма условий
равновесия (I форма)
II форма условий равновесия
Fkx 0
Fky 0
М (F ) 0
O k
М A ( Fk ) 0
М B ( Fk ) 0
Fkx 0
За моментную
точку (точка О)
может быть
выбрана любая
точка плоскости
Ось х не должна быть
перпендикулярной к
прямой, проходящей
через центры А и В
III форма условий
равновесия
М A ( Fk ) 0
М B ( Fk ) 0
М (F ) 0
C k
Центры А, В и С не
должны лежать на
одной прямой
11.
где :F
F
М
М
М
М
kx
0
- уравнение проекций всех сил на ось х
ky
0
- уравнение проекций всех сил на ось у
O
( Fk ) 0
A
( Fk ) 0
B
( Fk ) 0
C
( Fk ) 0
-уравнения моментов всех сил
относительно разных точек: O, A,
B, C.
Моментной может быть выбрана
любая точка плоскости.
12.
Важно !Для одного твердого тела можно составить
только три (!) независимых уравнения
равновесия по одной из предложенных
форм (I, II, III)
13.
Важно !В задаче на равновесие одного твердого
тела может быть только три неизвестные
силы (обычно это реакции связей). Тогда
задача будет статически определимой, то
есть решаемой!
14.
3.3. Виды сил, действующих натело
15.
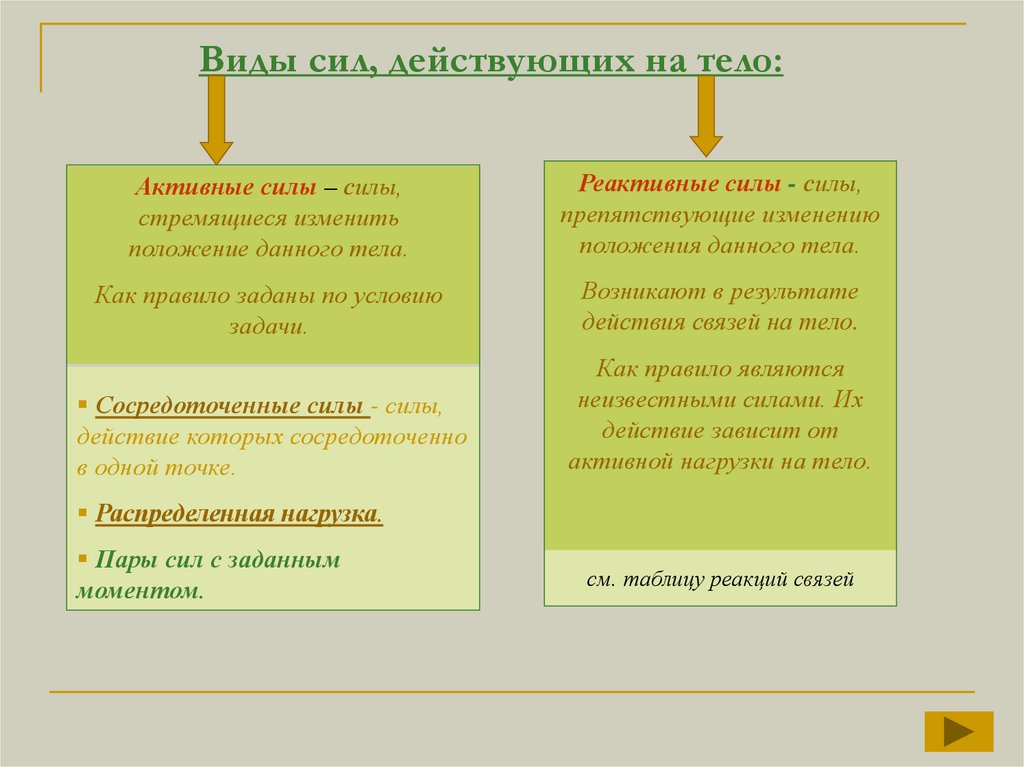
Виды сил, действующих на тело:Активные силы – силы,
стремящиеся изменить
положение данного тела.
Реактивные силы - силы,
препятствующие изменению
положения данного тела.
Как правило заданы по условию
задачи.
Возникают в результате
действия связей на тело.
Сосредоточенные силы - силы,
действие которых сосредоточенно
в одной точке.
Как правило являются
неизвестными силами. Их
действие зависит от
активной нагрузки на тело.
Распределенная нагрузка.
Пары сил с заданным
моментом.
см. таблицу реакций связей
16.
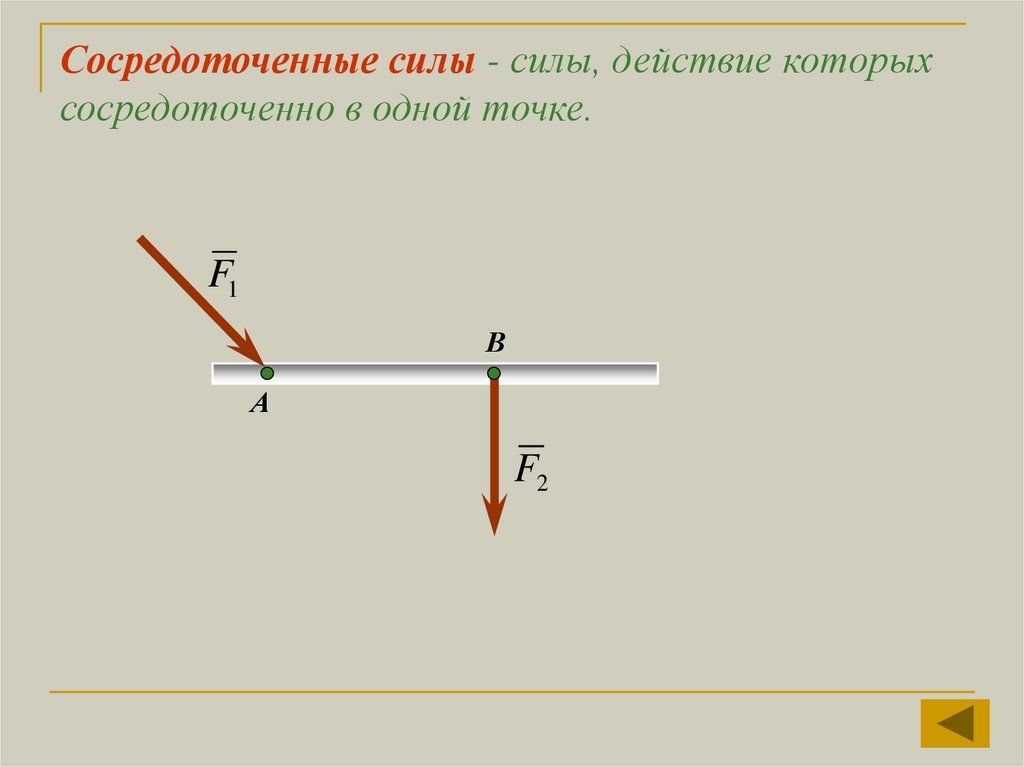
Сосредоточенные силы - силы, действие которыхсосредоточенно в одной точке.
F1
В
А
F2
17.
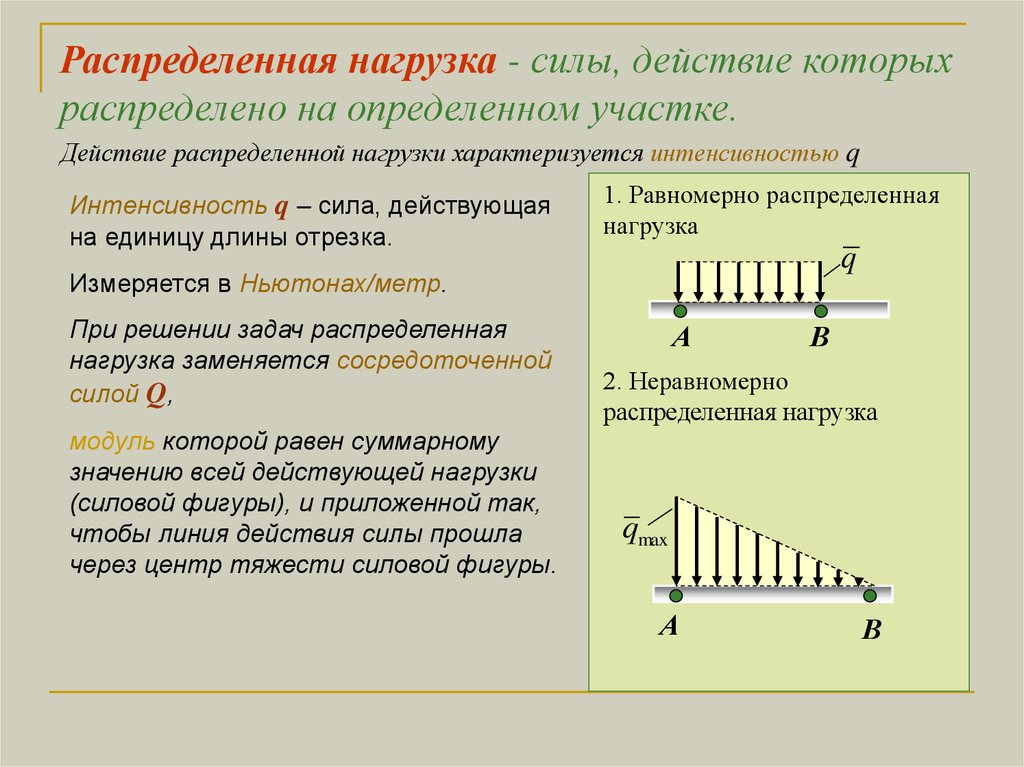
Распределенная нагрузка - силы, действие которыхраспределено на определенном участке.
Действие распределенной нагрузки характеризуется интенсивностью q
Интенсивность q – сила, действующая
на единицу длины отрезка.
1. Равномерно распределенная
нагрузка
q
Измеряется в Ньютонах/метр.
При решении задач распределенная
нагрузка заменяется сосредоточенной
силой Q,
модуль которой равен суммарному
значению всей действующей нагрузки
(силовой фигуры), и приложенной так,
чтобы линия действия силы прошла
через центр тяжести силовой фигуры.
А
В
2. Неравномерно
распределенная нагрузка
qmax
А
В
18.
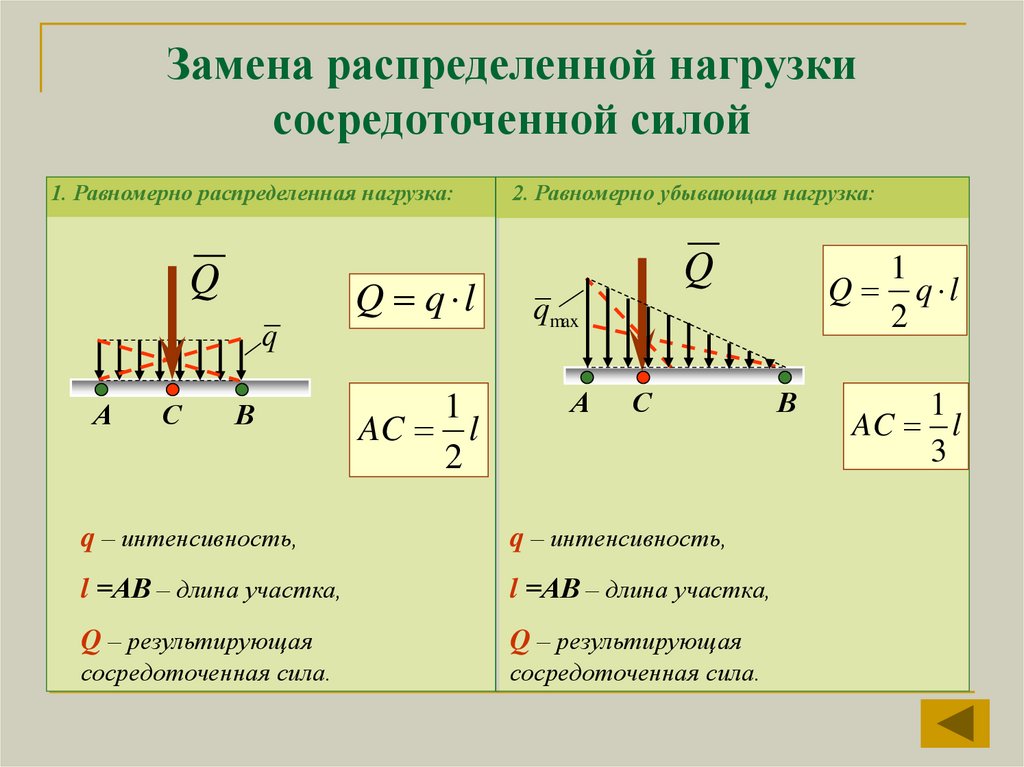
Замена распределенной нагрузкисосредоточенной силой
1. Равномерно распределенная нагрузка:
Q
Q q l
q
А
С
В
1
AC l
2
2. Равномерно убывающая нагрузка:
Q
Q
qmax
А
С
q – интенсивность,
q – интенсивность,
l =АВ – длина участка,
l =АВ – длина участка,
Q – результирующая
Q – результирующая
сосредоточенная сила.
сосредоточенная сила.
В
1
q l
2
1
AC l
3
19.
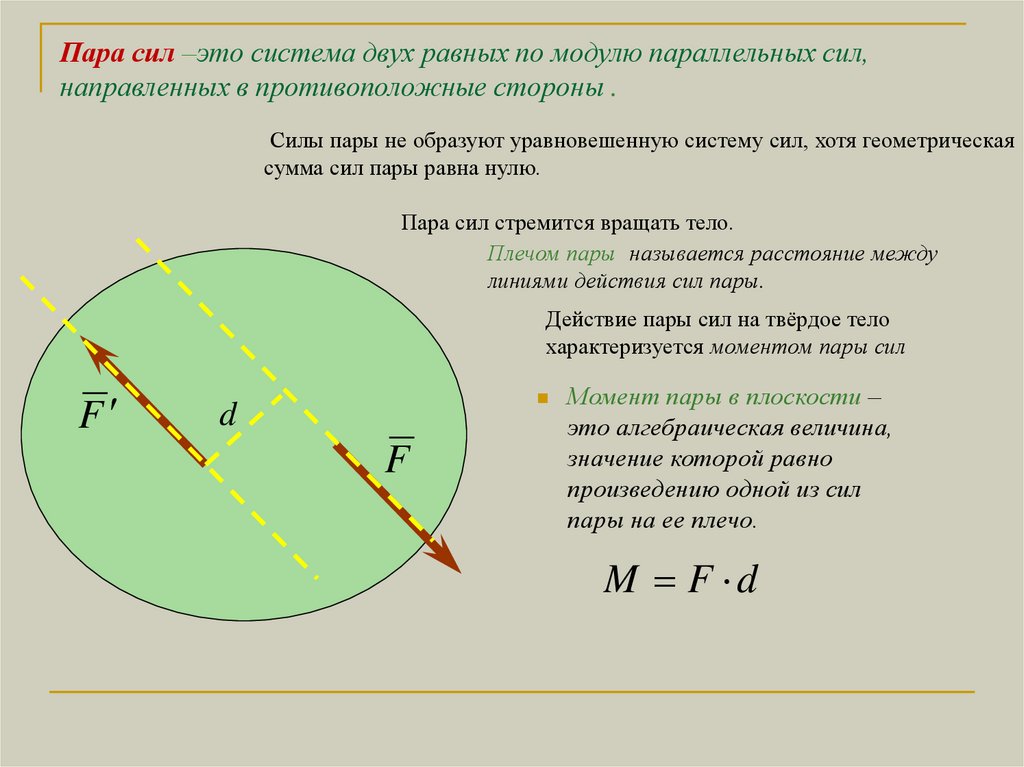
Пара сил –это система двух равных по модулю параллельных сил,направленных в противоположные стороны .
Силы пары не образуют уравновешенную систему сил, хотя геометрическая
сумма сил пары равна нулю.
Пара сил стремится вращать тело.
Плечом пары называется расстояние между
линиями действия сил пары.
Действие пары сил на твёрдое тело
характеризуется моментом пары сил
F
d
F
Момент пары в плоскости –
это алгебраическая величина,
значение которой равно
произведению одной из сил
пары на ее плечо.
M F d










 Физика
Физика








