Похожие презентации:
Решение задачи на равновесие плоской произвольной системы сил
1. РЕШЕНИЕ ЗАДАЧИ НА РАВНОВЕСИЕ ПЛОСКОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ
Мультимедийное учебное пособие по теоретической механикеРЕШЕНИЕ ЗАДАЧИ НА
РАВНОВЕСИЕ ПЛОСКОЙ
ПРОИЗВОЛЬНОЙ СИСТЕМЫ
СИЛ
Солодовник Е.В.
Г. Хабаровск
Тихоокеанский государственный университет
2. Определение реакций связей твердого тела
Практическое занятие №43.
Три формы уравнений равновесия для плоской произвольной системысил
Основная форма условий
равновесия (I форма)
II форма условий равновесия
Fkx 0
Fky 0
М (F ) 0
O k
М A ( Fk ) 0
М B ( Fk ) 0
Fkx 0
За моментную
точку (точка О)
может быть
выбрана любая
точка плоскости
Ось х не должна быть
перпендикулярной к
прямой, проходящей
через центры А и В
III форма условий
равновесия
М A ( Fk ) 0
М B ( Fk ) 0
М (F ) 0
C k
Центры А, В и С не
должны лежать на
одной прямой
4.
где :F
F
М
М
М
М
kx
0
- уравнение проекций всех сил на ось х
kx
0
- уравнение проекций всех сил на ось у
O
( Fk ) 0
A
( Fk ) 0
B
( Fk ) 0
C
( Fk ) 0
-уравнения моментов всех сил
относительно разных точек: O, A,
B, C.
Моментной может быть выбрана
любая точка плоскости.
5. Важно !
O Для одного твердого тела можносоставить только три (!) независимых
уравнения равновесия по одной из
предложенных форм (I, II, III)
6. Важно !
O В задаче на равновесие одноготвердого тела может быть только три
неизвестные силы (обычно это реакции
связей). Тогда задача будет статически
определимой, то есть решаемой!
7. Методика решения задач:
1. Выделить тело, равновесие которого рассматривается2. Изобразить активные (заданные) силы
3. Освободить тело от связей, приложив соответствующие реакции.
4. Направить оси координат и выбрать моментные точки.
5. Составить уравнения равновесия для произвольной плоской системы сил.
6. Решить систему полученных уравнений равновесия. Найти неизвестные величины.
8. Полезно помнить, что :
O уравнение моментов будет болеепростым (содержать меньше
неизвестных), если брать моменты
относительно точки, где пересекаются
линии действия двух реакций связей.
9. Полезно помнить, что :
O при вычислении момента силы частобывает удобно воспользоваться теоремой
Вариньона, то есть разложить силу на
проекции, для которых легко
определяются плечи, и тогда момент
силы определяется как сумма моментов
ее проекций относительно той же точки.
М O F М O Fх М O Fу .
10.
Пример 3На балку, свободно
опирающуюся в точках А и В и имеющую
подвижный шарнир в
точке С, действуют:
силы Р1= 30 кН, Р2= 20
кН и Р3= 50 кН, и
сосредоточенный
момент М = 150 кН∙м.
Размеры заданны в
метрах.
Определить реакции в
опорах.
Дано:
Р1= 30 кН, Р2= 20 кН, Р3= 50 кН, М = 150
кН∙м.
Найти: реакции связей.
Р1
М
А
В
С
Р2
Р3
1
2
3
2
450
11.
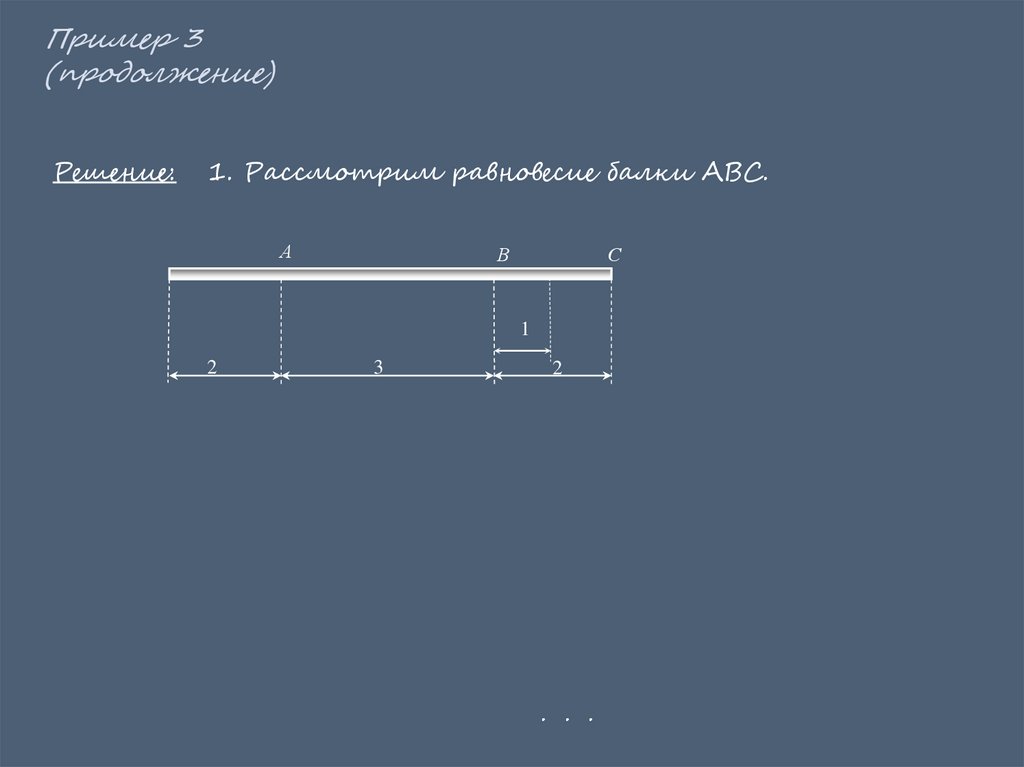
Пример 3(продолжение)
Решение:
1. Рассмотрим равновесие балки АВС.
А
В
С
1
2
3
2
. . .
12.
Пример 3(продолжение)
Решение:
М
Р1
А
В
Р2
С
1
2
3
Р3
2
2. К ней приложены активные нагрузки
Р1,
Р2, Р3
и
сосредоточенный момент М.
. . .
13.
Пример 3(продолжение)
Решение:
М
Р1
А
В
Р2
С
Р3
1
2
3
450
2
3. Связями в точках А и В являются точечные опоры, в
точке С – стержень ..
. . .
14.
Пример 3(продолжение)
Решение:
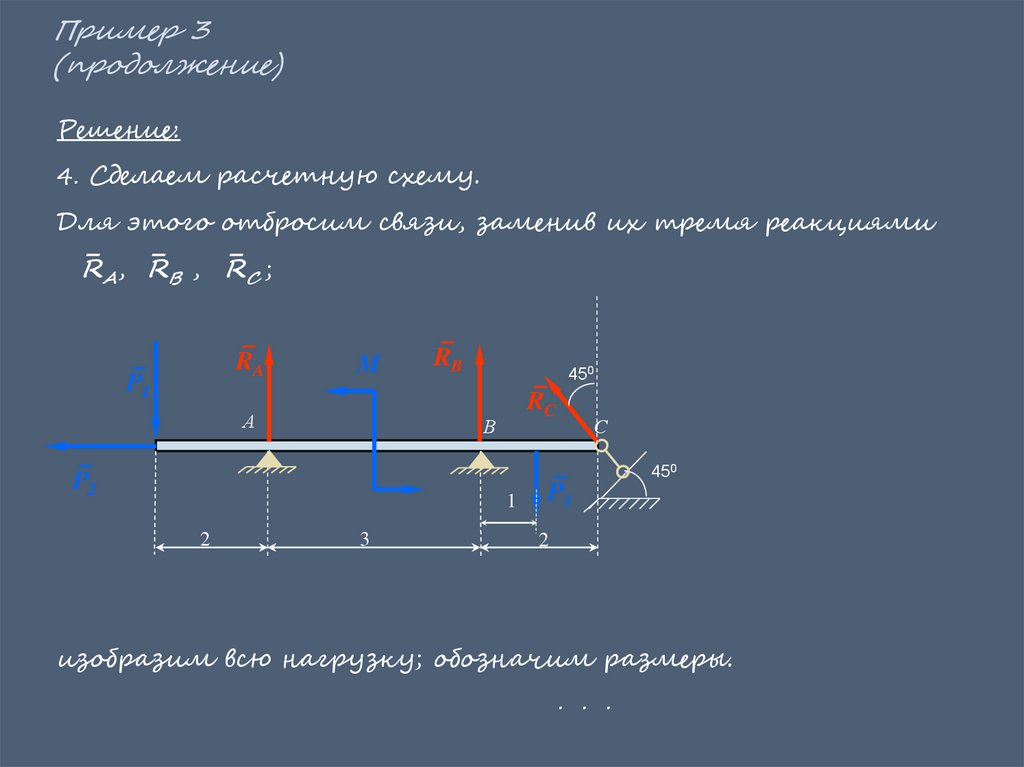
4. Сделаем расчетную схему.
Для этого отбросим связи, заменив их тремя реакциями
RA, RB , RC ;
RA
Р1
М
А
RB
В
Р2
RC
1
2
3
450
С
Р3
450
2
изобразим всю нагрузку; обозначим размеры.
. . .
15.
Пример 3(продолжение)
E
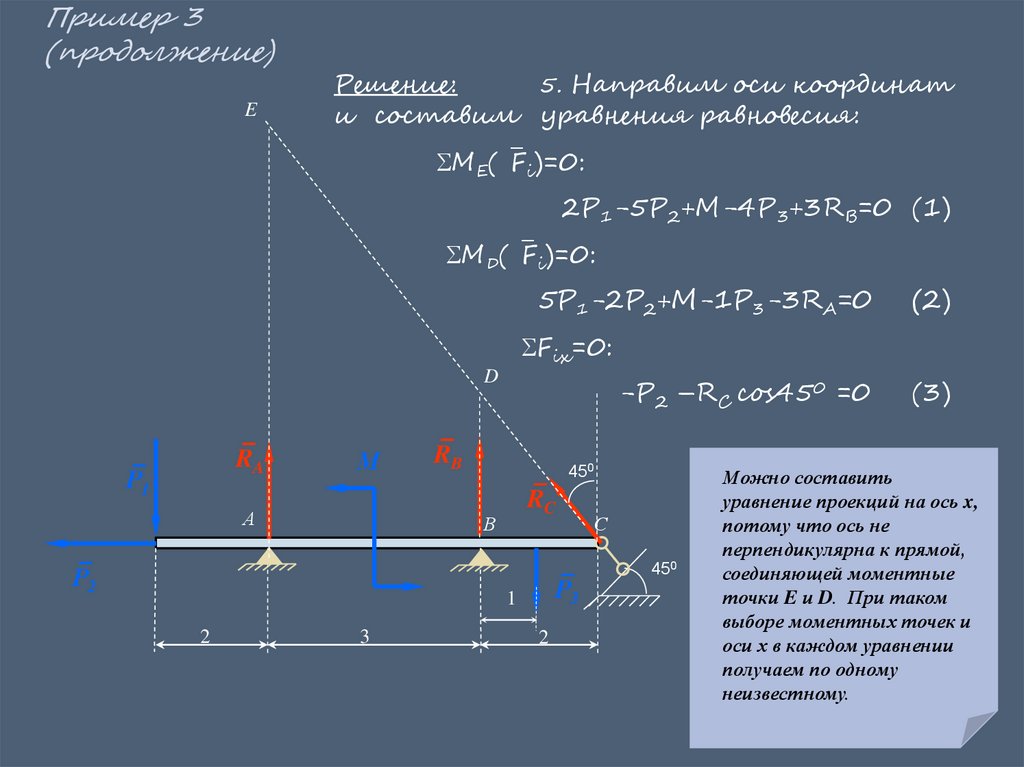
Решение:
5. Направим оси координат
и составим уравнения равновесия:
МЕ( Fi)=0:
2P1-5P2+M-4P3+3RB=0 (1)
МD( Fi)=0:
5P1-2P2+M-1P3-3RA=0
(2)
Fix=0:
D
RA
Р1
М
А
RB
В
Р2
-P2 –RC cos450 =0
RC
1
2
3
450
Р3
2
С
450
(3)
Можно составить
уравнение проекций на ось x,
потому что ось не
перпендикулярна к прямой,
соединяющей моментные
точки E и D. При таком
выборе моментных точек и
оси х в каждом уравнении
получаем по одному
неизвестному.
16.
Пример 3(продолжение)
Решение:
6. Решая полученные уравнения (1), (2), (3) относительно искомых
реакций, получим:
RB = (-2P1+5P2-M+4P3)/3 = 30 кН
RA = (5P1-2P2+M-P3)/3 = 70
кН
RC = -P2 / cos450 = 28,28 кН
. . .
17.
Пример 3(продолжение)
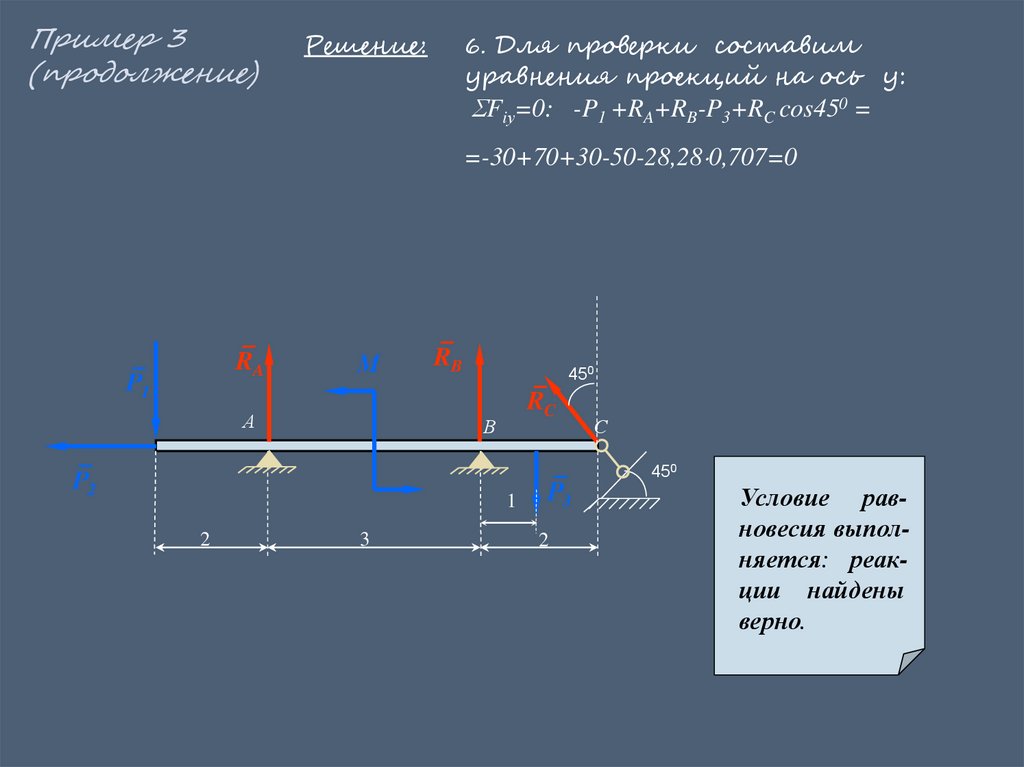
Решение:
6. Для проверки составим
уравнения проекций на ось у:
Fiу=0: -P1 +RA+RB-P3+RC cos450 =
=-30+70+30-50-28,28 0,707=0
RA
Р1
М
А
RB
В
Р2
RC
1
2
3
450
Р3
2
С
450
Условие равновесия выполняется: реакции найдены
верно.













 Физика
Физика








