Похожие презентации:
Решение задач на равновесие плоской произвольной системы сил. Практическое занятие
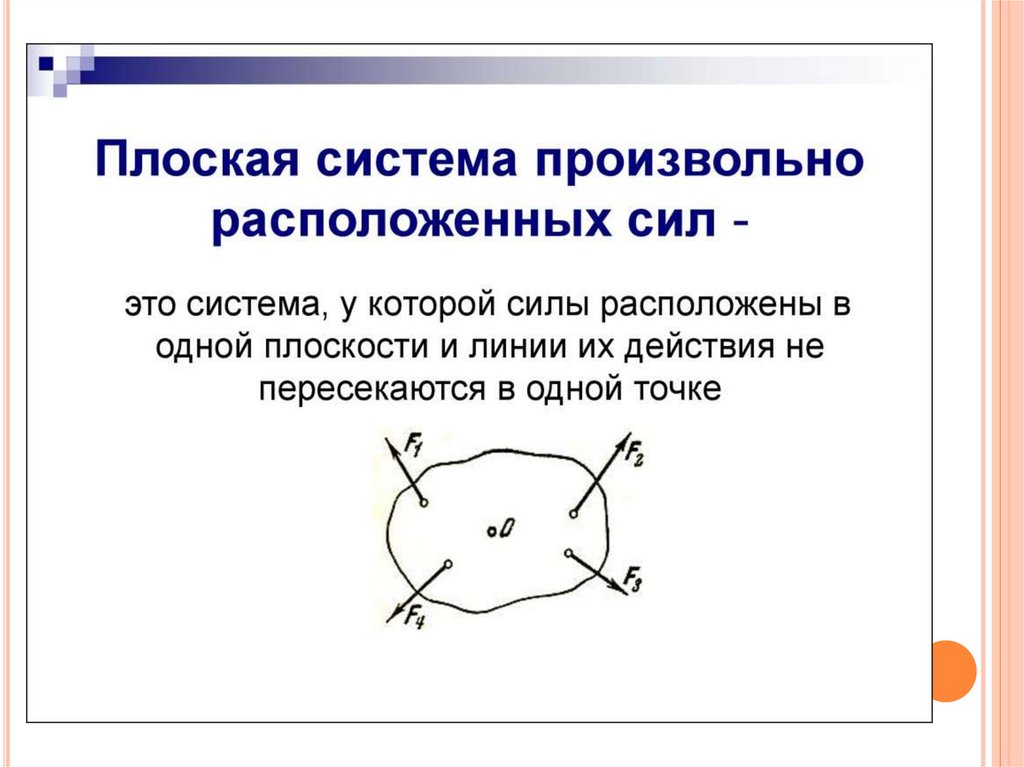
1.
2.
3.
«ДляУСЛОВИЕ РАВНОВЕСИЯ:
равновесия плоской произвольной системы
сил, необходимо и достаточно, чтобы суммы
проекций всех заданных сил на оси х и у равнялись
нулю, а так же сумма моментов всех сил
относительно любой точки плоскости тоже
равнялась нулю.»
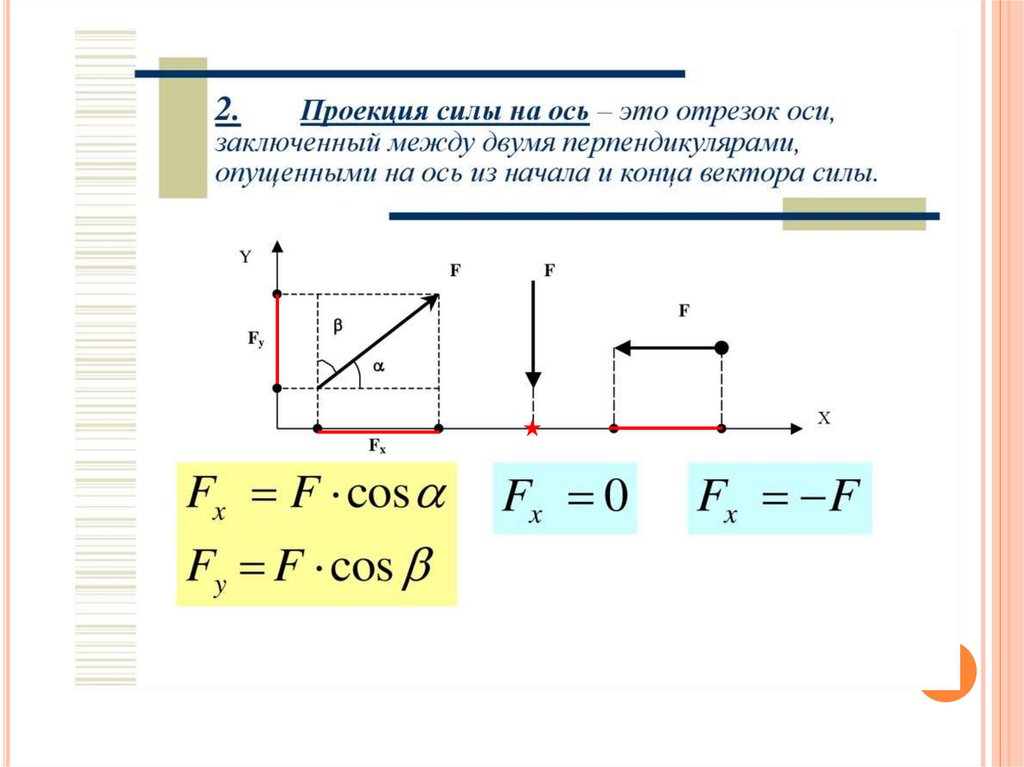
F
F
кx
кy
0
0
М 0 ( Fк ) 0
! Рациональнее для составления уравнения
моментов лучше выбирать точку, в которой
сходятся большее количество неизвестных
сил.
4.
Теорема Вариньона.Для удобства составления моментов сил относительно
точки удобно использовать теорему Вариньона:
mA(
F
5.
6.
ПОРЯДОКРАСЧЕТА ПЛОСКОЙ
ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ:
1)
Изобразить тело, обозначив
внешние (активные) силы,
распределенные нагрузки заменить
сосредоточенными силами.
2) Выяснить виды связей, обозначить
на рисунке реакции.
3) Записать условия равновесия и
составить уравнения равновесия.
4) Найти неизвестные реакции, решив
уравнения.
5) Сделать проверку правильности
решения.
7.
М8.
РАСПРЕДЕЛЁННАЯ НАГРУЗКАq — интенсивность
нагрузки, кН/м;
l — длина стержня, м
q
l/2
Q
Равнодействующа
я распределенной
нагрузки
Q прикладывается в
центре нагрузки и
направлена в
сторону показанных
линий
интенсивности
9.
ПАРА СИЛ И МОМЕНТСИЛЫ ОТНОСИТЕЛЬНО
ТОЧКИ
10.
1.ПАРА СИЛ – ЭТО СИСТЕМА ДВУХ, РАВНЫХ ПО
МОДУЛЮ, ПРОТИВОПОЛОЖНЫХ ПО НАПРАВЛЕНИЮ
ПАРАЛЛЕЛЬНЫХ СИЛ.
Эффект
действия пары
– вращение.
Вращение
характеризуе
тся
моментом.
11.
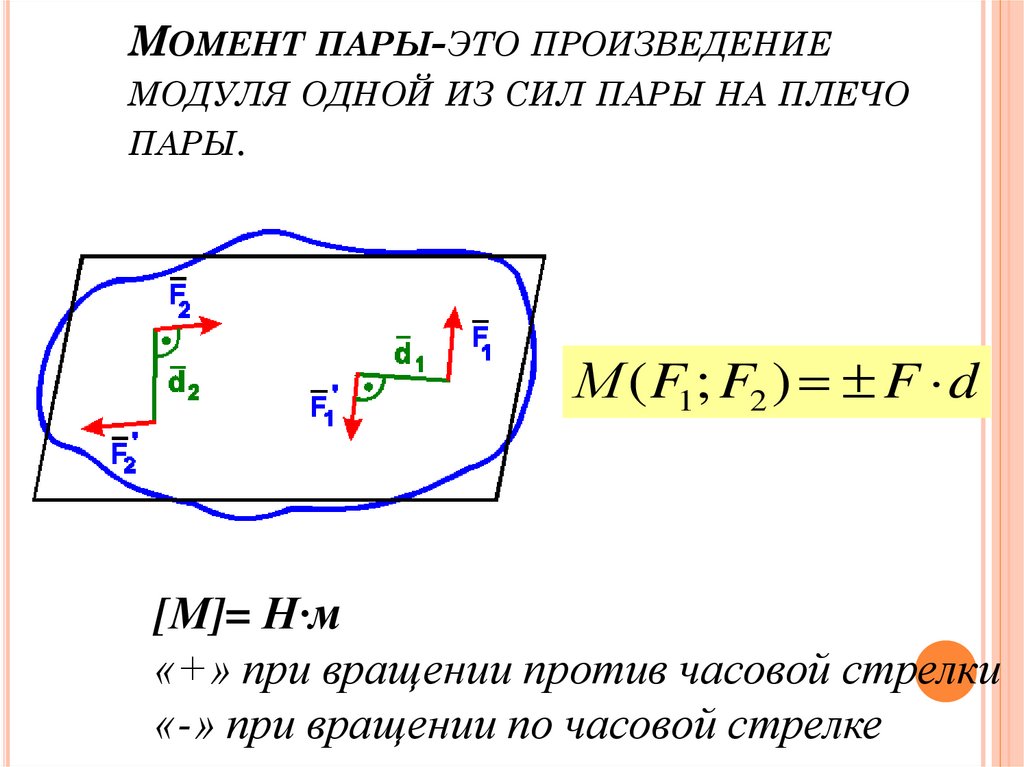
МОМЕНТ ПАРЫ-ЭТО ПРОИЗВЕДЕНИЕМОДУЛЯ ОДНОЙ ИЗ СИЛ ПАРЫ НА ПЛЕЧО
ПАРЫ.
М ( F1; F2 ) F d
[М]= Н·м
«+» при вращении против часовой стрелки
«-» при вращении по часовой стрелке
12.
ВРАЩАТЕЛЬНОЕ ДЕЙСТВИЕ СИЛЫХАРАКТЕРИЗУЕТСЯ МОМЕНТОМ.
Момент
силы относительно
точки -это произведение модуля силы
на её плечо.
М (F ) F h
( Н м)
13.
14.
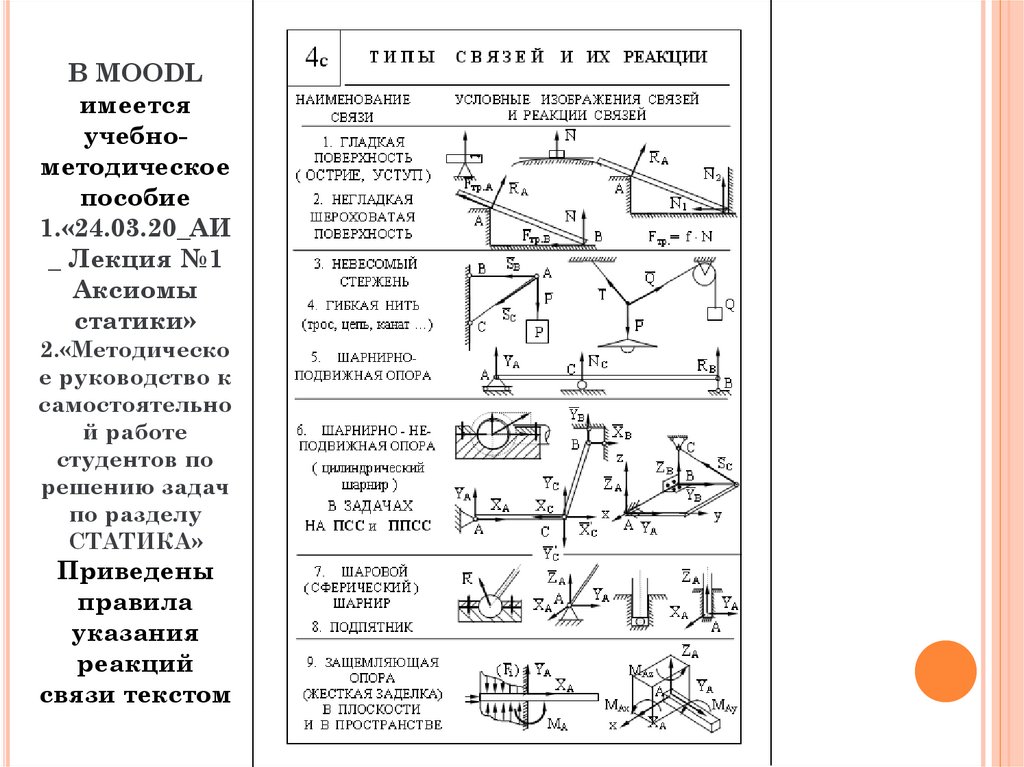
В MOODLимеется
учебнометодическое
пособие
1.«24.03.20_АИ
_ Лекция №1
Аксиомы
статики»
2.«Методическо
е руководство к
самостоятельно
й работе
студентов по
решению задач
по разделу
СТАТИКА»
Приведены
правила
указания
реакций
связи текстом
15.
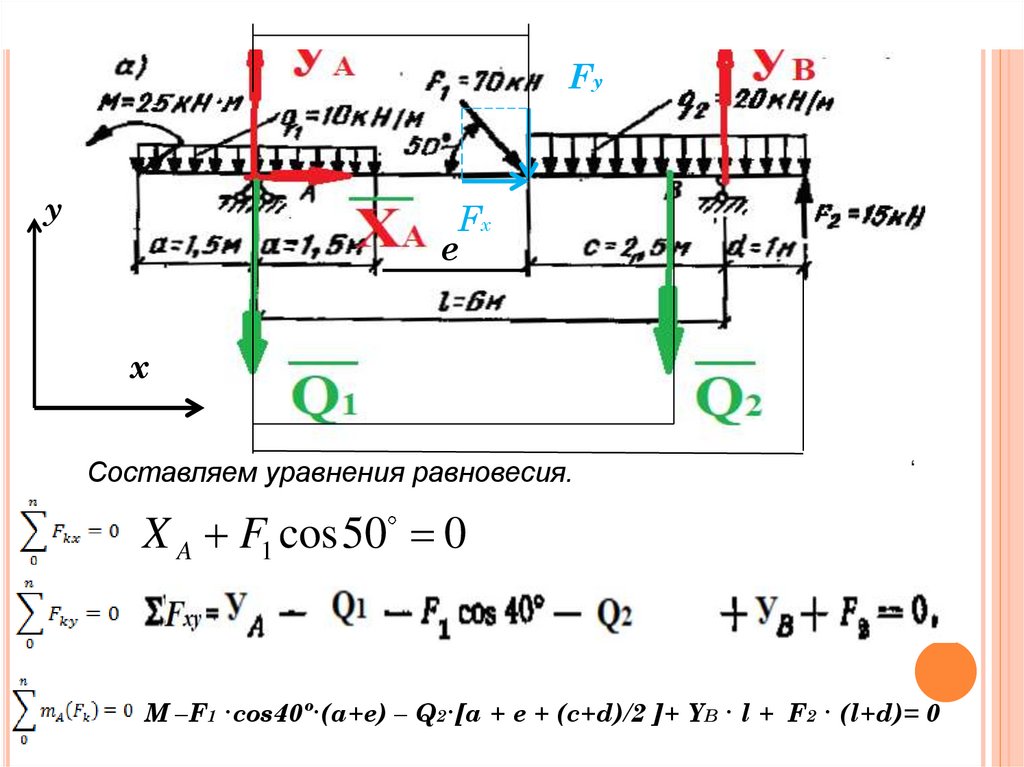
Пример 2. Определить опорные реакции балки, показанной нарисунке 1.
Рис.1
15
16.
Решение: 1. Освобождаемся от опор и заменяем ихдействие реакциями опор. Левая опора в точке А
неподвижный цилиндрический шарнир, в ней надо по
правилу показать две составляющие силы реакции УA и ХA.
Правая опора в точке В идеальный стержень, в нём
возникает одна реакция направленная вдоль линии,
соединяющей шарниры стержня - вертикальная сила УB
17.
РАСПРЕДЕЛЁННАЯ НАГРУЗКАq — интенсивность
нагрузки, кН/м;
l — длина стержня, м
q
l/2
Q
Равнодействующа
я распределенной
нагрузки
Q прикладывается в
центре нагрузки и
направлена в
сторону показанных
линий
интенсивности
18.
Заменим распределённые нагрузки распределёнными силами Q1 иQ2, которые приложим в центре каждой нагрузки и направим по
направлению стрелок интенсивности. Найдём величины этих сил:
Q1 = q1·2a= 10·3=30кH ;
Q2 = q2 ·(c+d)= 20·3,5=70кH ;
18
19.
20.
Fyy
Fx
e
x
,
Составляем уравнения равновесия.
X A F1 cos50 0
М –F1 ·cos40º·(a+e) – Q2·[a + e + (c+d)/2 ]+ YB · l + F2 · (l+d)= 0

















 Физика
Физика








