Площадь криволинейной трапеции и интеграл

1. Площадь криволинейной трапеции и интеграл.

у
х

2.

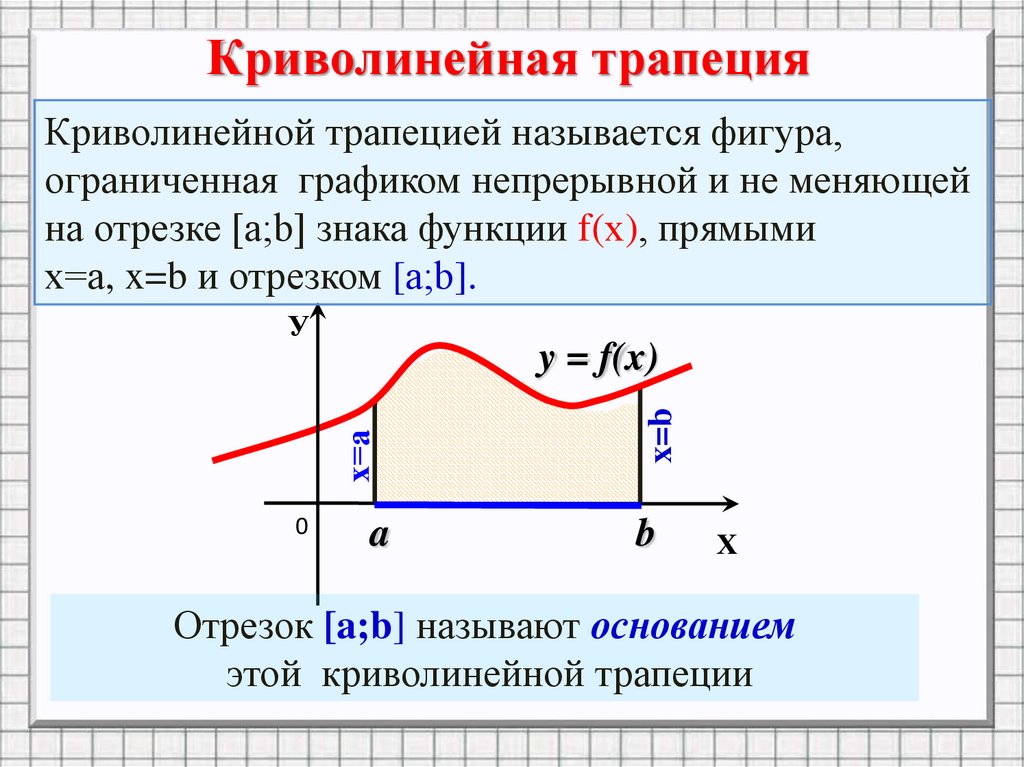
Криволинейная трапеция
Криволинейной трапецией называется фигура,
ограниченная графиком непрерывной и не меняющей
на отрезке [а;b] знака функции f(х), прямыми
х=а, x=b и отрезком [а;b].
У
0
a
x=b
х=а
y = f(x)
b
Х
Отрезок [a;b] называют основанием
этой криволинейной трапеции

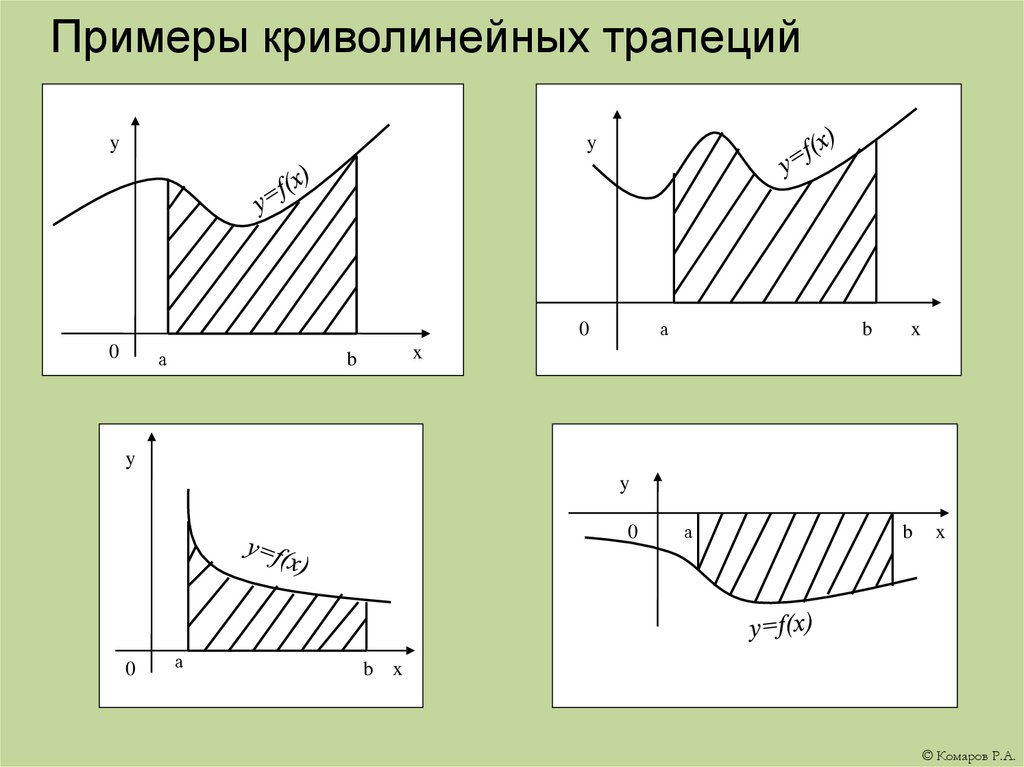
3. Примеры криволинейных трапеций

y
y
а
0
0
а
b
x
x
b
y
y
0
0
а
а
b
x
b x
© Комаров Р.А.

4.

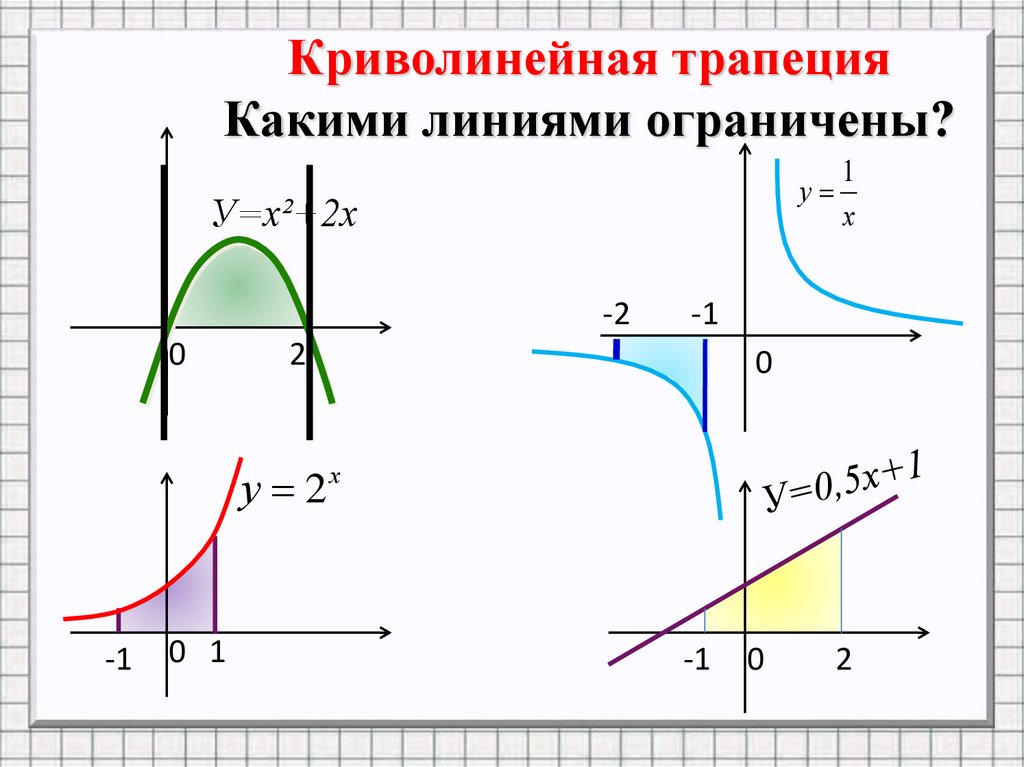
Криволинейная трапеция
Какими линиями ограничены?
у
У=х²+2х
-2
0
-1
0 1
-1
2
у 2
1
х
0
х
-1
0
2

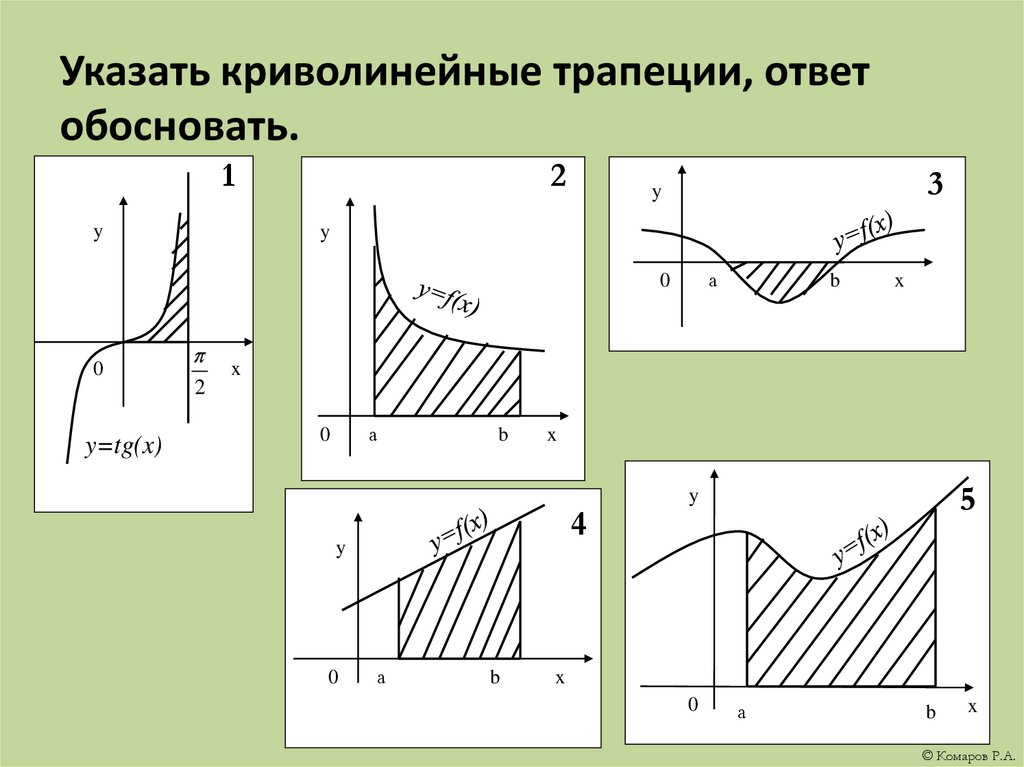
5. Указать криволинейные трапеции, ответ обосновать.

1
y
2
3
y
y
а
0
0
y=tg(x)
2
b
x
x
а
0
b
x
4
y
0
а
b
5
y
x
0
а
b
x
© Комаров Р.А.

6.

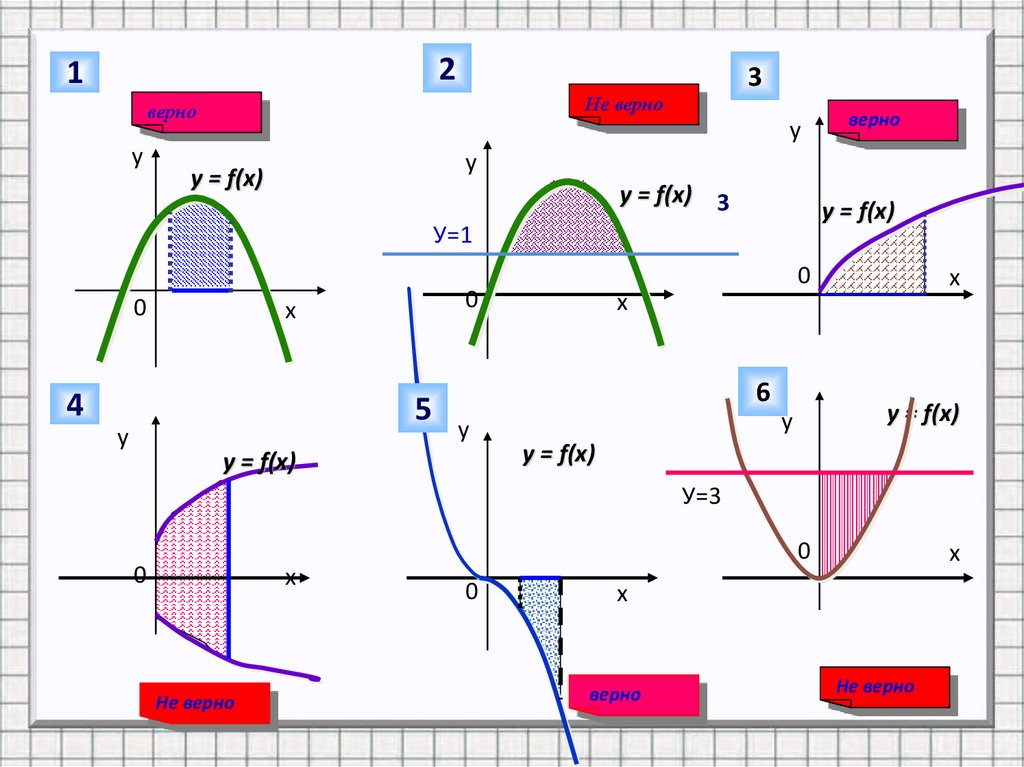
Какие из заштрихованных на рисунке
фигур являются криволинейными
трапециями, а какие нет?

7.

2
1
Не верно
верно
у
3
у
у
y = f(x)
y = f(x) 3
y = f(x)
У=1
0
0
0
х
4
5
у
верно
х
6
у
y = f(x)
х
y = f(x)
у
y = f(x)
У=3
0
0
х
Не верно
0
х
х
верно
Не верно

8. Изобразить криволинейную трапецию, ограниченную графиком функции y = (x-1)2, осью Ox и прямой x=2.

y x 1
2
1
0
1
01
x=2
y
12
x

9. Определённый интеграл

10. Задачи, приводящие к понятию определённого интеграла

Решение различных задач привело
к одной и той же математической модели:
Для функции y=f(x) на отрезке [a;b]:
1.Разбить отрезок [a;b] на n равных частей
2.Составить сумму Sn =f(x0)·∆x0+…+ f(xn)·∆xn
3.Вычислить предел этой суммы при n→∞

11. Понятие определённого интеграла

Предел такой суммы называют
определённым интегралом по отрезку [a;b]:
b – верхний
предел
b
a
f ( x)dx
а – нижний
предел

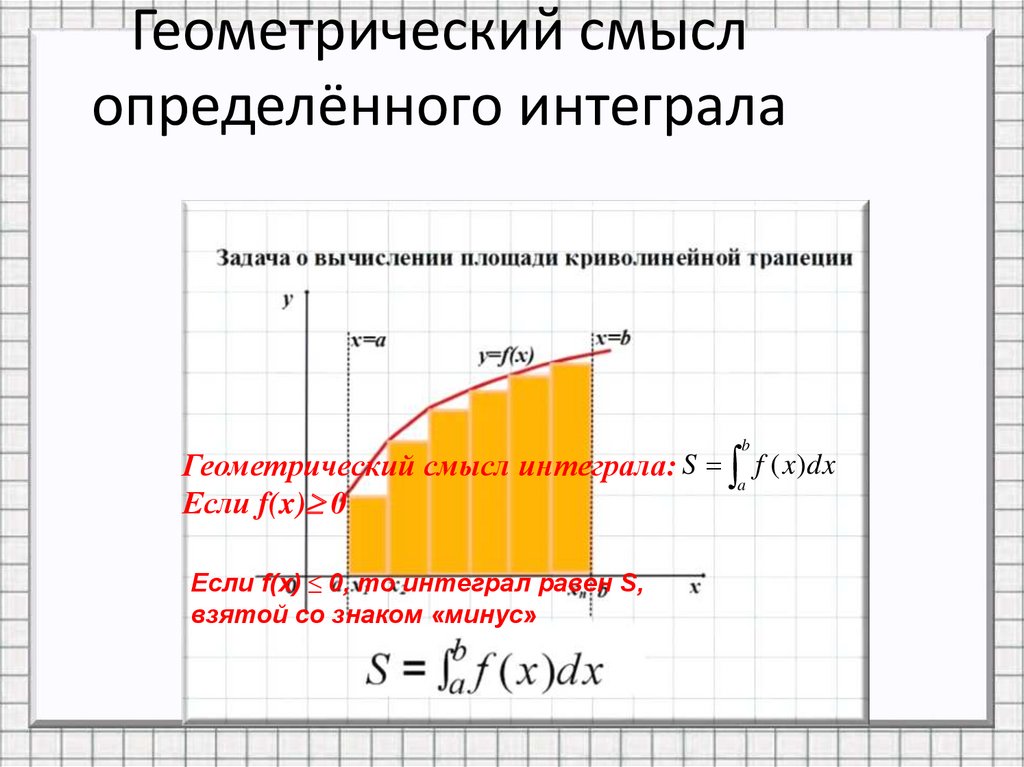
12. Геометрический смысл определённого интеграла

Геометрический смысл интеграла: S a f ( x)dx
Если f(x) 0
b
Если f(x) ≤ 0, то интеграл равен S,
взятой со знаком «минус»

13. Формула Ньютона-Лейбница

Урок №2

14. Формула Ньютона-Лейбница

b
f ( x)dx F (b) F (a ),
a
где F(x) – первообразная
для функции f(x)
Исаак Ньютон
1642-1727
b
b
Или
a
f ( x)dx F ( x)
a
Готфрид Лейбниц
1646-1716

15.

Формула Ньютона-Лейбница
Ньютон открыл новый метод раньше, но
опубликовал его позже Лейбница, написав ему:
«Надеюсь, что я при этом не написал ничего,
что было бы тебе неприятно, если же это
случилось, то прошу сообщить, потому что
друзья мне дороже математических открытий»
Лейбниц ответил в резкой форме. Распря двух
гениев дорого обошлась науке: английская
математическая школа увяла на целый век,
а европейская проигнорировала многие
выдающиеся идеи Ньютона.
Спор тянулся почти 40 лет, пока аббат Конти не
сообщил Ньютону: «Лейбниц умер – диспут окончен»

16. Вычисление определённого интеграла

Вычислить интеграл:
2
2
2
2
2 Формула
Постоянный
множитель
Ньютона-Лейбница:
dx можно
от
суммы
функций
равен
3 вынести
( 2 Интеграл
3x3 1за
)dx
2
3
x
dx
dx
2
знак
интеграла
сумме интегралов
x
x
1
1
2
1
4 2
1
4
2
1
x
2 3x
2
b 2( ) 3
x b1 ( b x)
xf ( x1 b)dx4 1F ( x) b Fx (b)4 F (a )1
( f ( x) gkf( x( x)))dx k f (fx()xdx
)dx g ( x)dx
a
3 a aa
1 a
a
a
( 1 12 2) (2 1) 11
4
4
1
Ответ : 11
4
b
b

17. Геометрический смысл определённого интеграла

3
Вычислить интеграл
f ( x)dx,
y
2
если график функции y=f(x)
изображён на рисунке
4
1
-2
Ответ: 9,5
3
x

18.

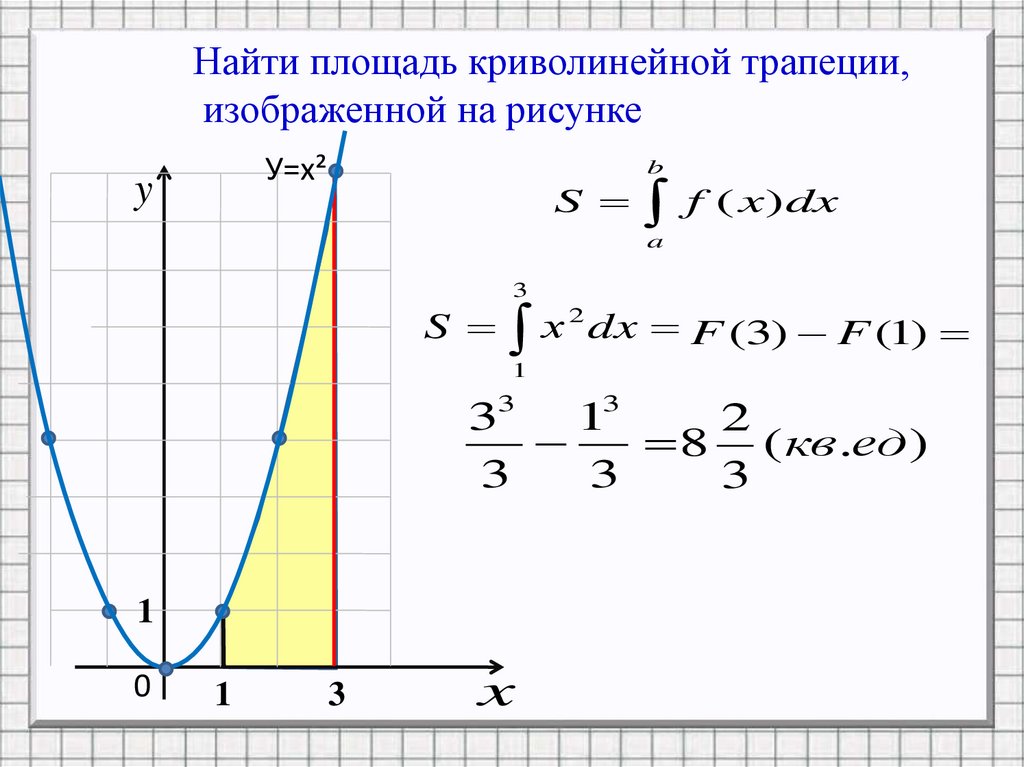
Найти площадь криволинейной трапеции,
изображенной на рисунке
У=х²
y
b
S
f ( x) dx
a
3
S
х 2 dx F (3) F (1)
1
33 13
2
8 ( кв .ед)
3
3
3
1
0
1
3
x

19.

Найти площадь криволинейной трапеции,
изображенной на рисунке
y
I
1
0
I
-1
y=sinx
2
x