Похожие презентации:
Площадь криволинейной трапеции и интеграл
1. Площадь криволинейной трапеции и интеграл.
2.
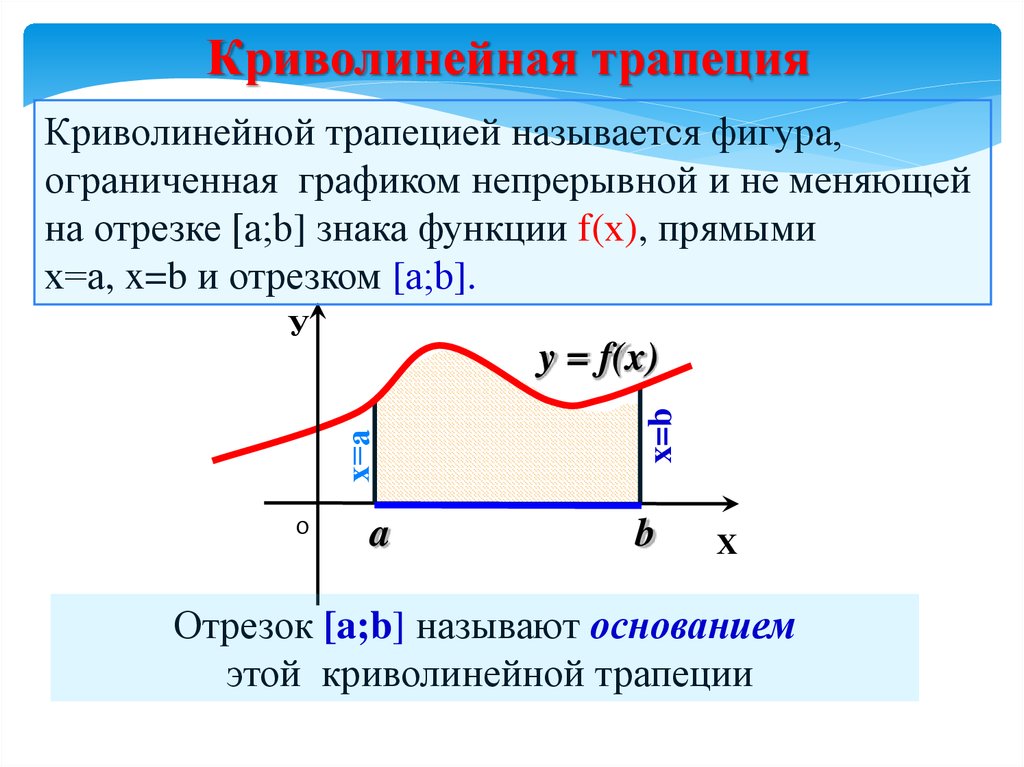
Криволинейная трапецияКриволинейной трапецией называется фигура,
ограниченная графиком непрерывной и не меняющей
на отрезке [а;b] знака функции f(х), прямыми
х=а, x=b и отрезком [а;b].
У
0
a
x=b
х=а
y = f(x)
b
Х
Отрезок [a;b] называют основанием
этой криволинейной трапеции
3.
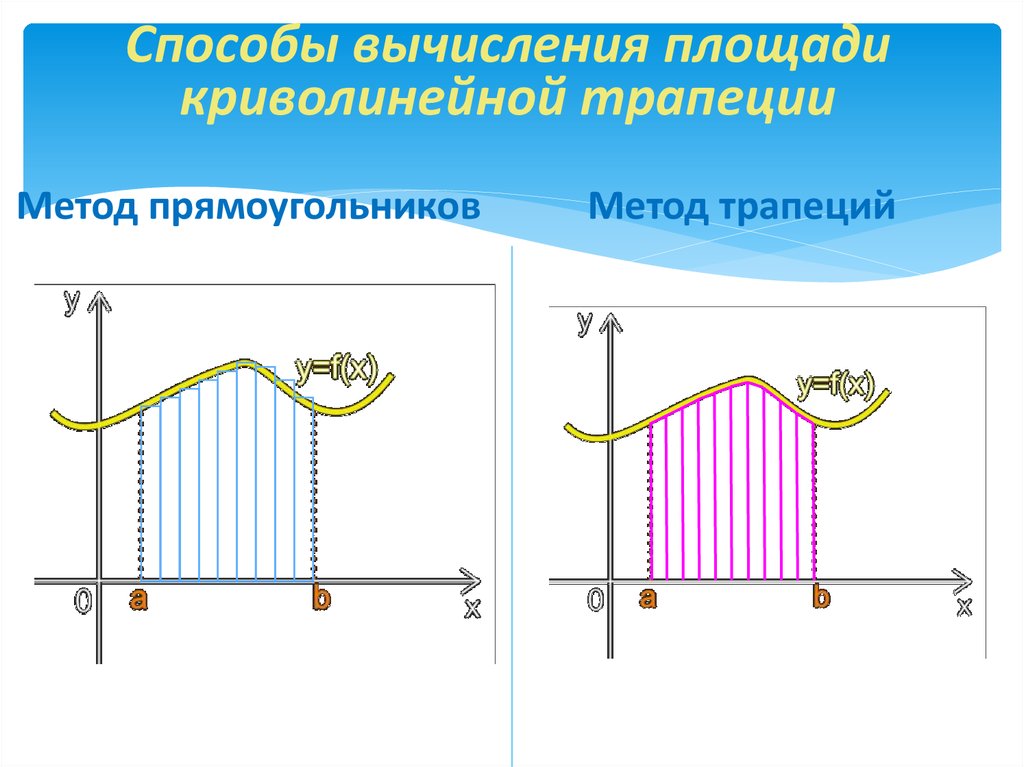
Способы вычисления площадикриволинейной трапеции
Метод прямоугольников
Метод трапеций
4.
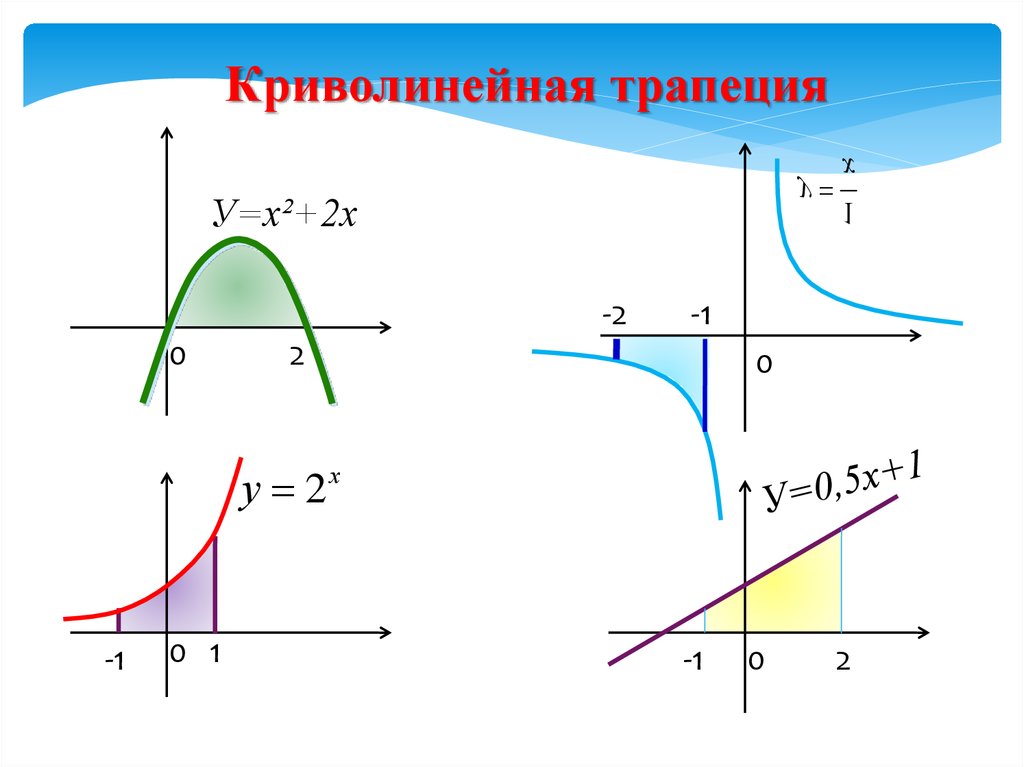
Криволинейная трапециях
у
1
У=х²+2х
-2
0
2
у 2
-1
0 1
-1
0
х
-1
0
2
5.
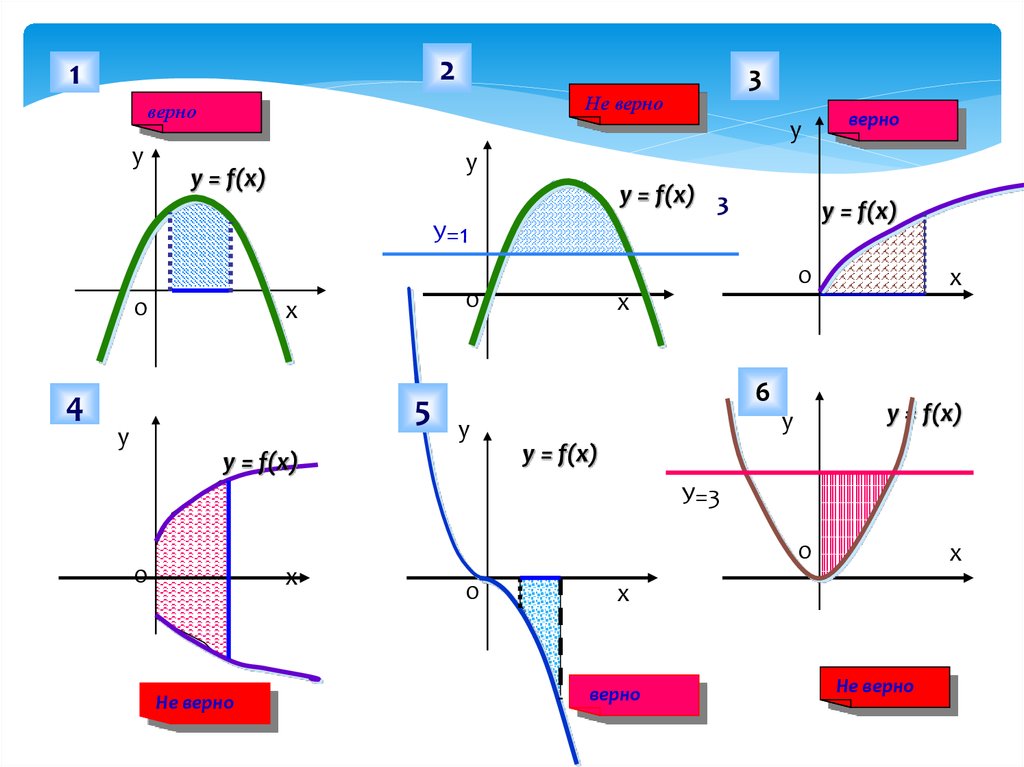
Какие из заштрихованных на рисункефигур являются криволинейными
трапециями, а какие нет?
Заполнить таблицу
№1
№2
№3
№4
№5
№6
Да/нет
6.
21
Не верно
верно
у
3
у
у
y = f(x)
y = f(x) 3
y = f(x)
У=1
0
0
0
х
4
5
у
верно
х
6
у
y = f(x)
х
y = f(x)
у
y = f(x)
У=3
0
0
х
Не верно
0
х
х
верно
Не верно
7. Площадь криволинейной трапеции
Теорема. Любая функция f(х), непрерывная на отрезке [a;b] иимеющая на нем конечное количество экстремумов, имеет на
этом отрезке первообразную.
8.
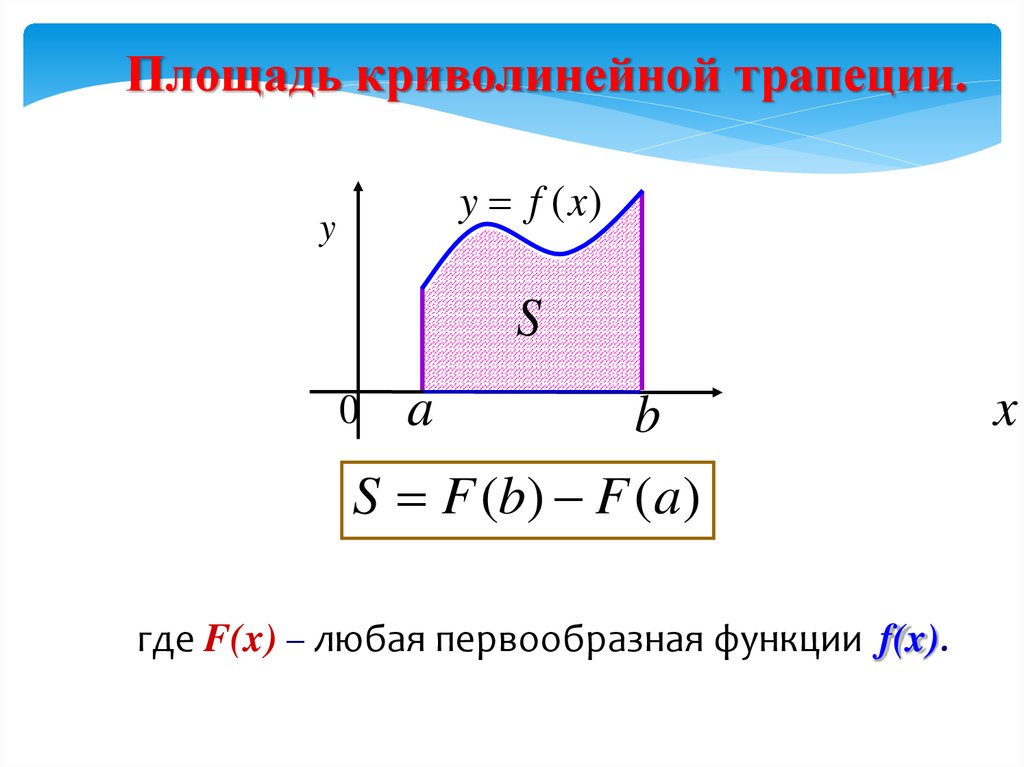
Площадь криволинейной трапеции.y f (x)
y
S
0
a
b
S F (b) F (a)
где F(x) – любая первообразная функции f(x).
x
9.
Формула Ньютона-ЛейбницаS F (b) F (a)
b
f ( x)dx F (b) F (a)
a
b
1643—1727
f ( x)dx F (b) F (a)
a
b
S f ( x)dx
a
1646—1716
10. Алгоритм вычисления площади криволинейной трапеции:
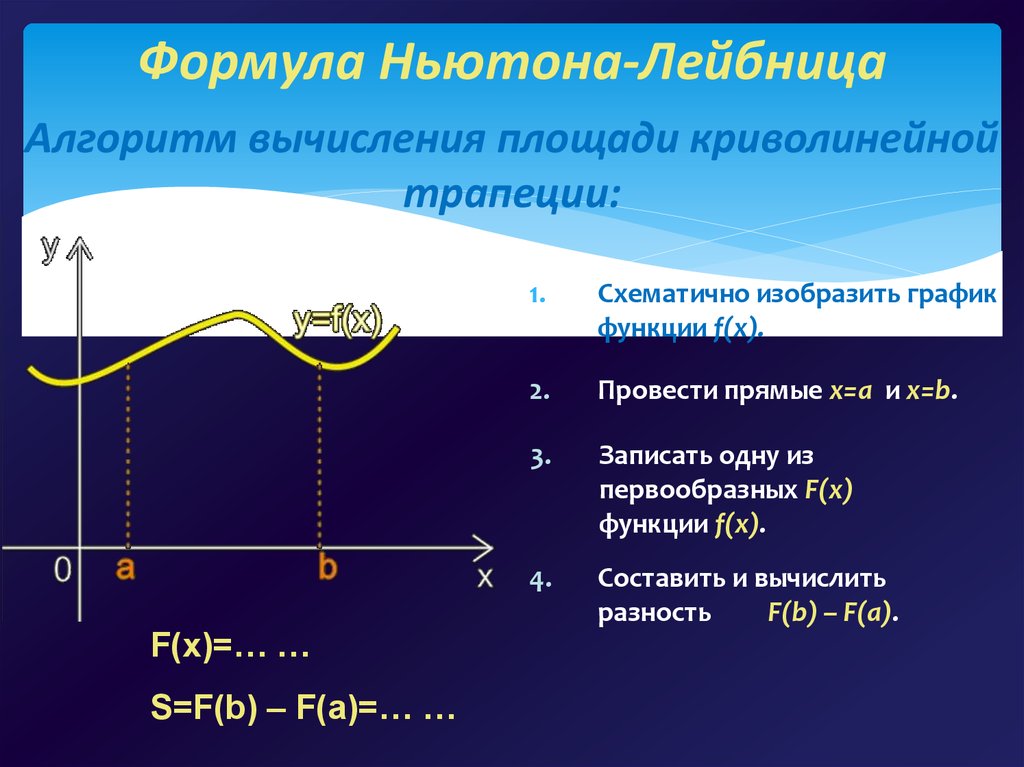
Формула Ньютона-ЛейбницаАлгоритм вычисления площади криволинейной
трапеции:
F(x)=… …
S=F(b) – F(a)=… …
1.
Схематично изобразить график
функции f(x).
2.
Провести прямые x=a и x=b.
3.
Записать одну из
первообразных F(x)
функции f(x).
4.
Составить и вычислить
разность
F(b) – F(a).
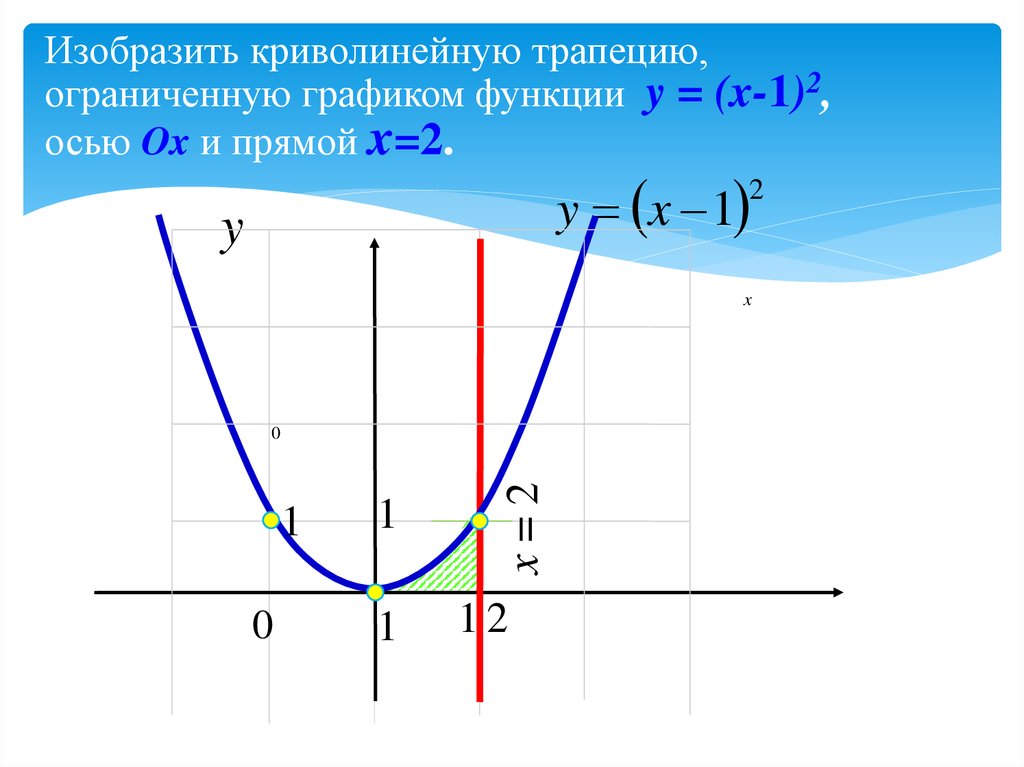
11. Изобразить криволинейную трапецию, ограниченную графиком функции y = (x-1)2, осью Ox и прямой x=2.
y x 12
y
x
1
0
1
1
x=2
0
12
12.
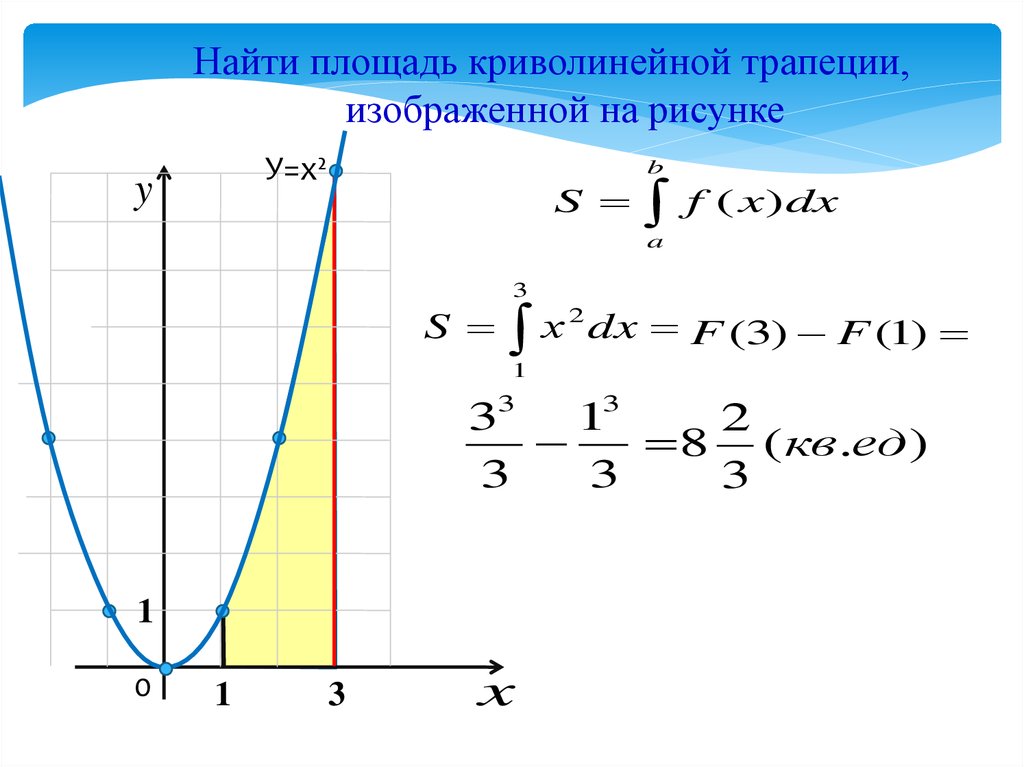
Найти площадь криволинейной трапеции,изображенной на рисунке
У=х²
y
b
S
f ( x) dx
a
3
S
х 2 dx F (3) F (1)
1
33 13
2
8 ( кв .ед)
3
3
3
1
0
1
3
x
13.
Формулы вычисления площади с помощьюинтеграла
у
у
у=f(x)
у=f(x)
x
а
х
a
b
b
14.
Формулы вычисления площади спомощью интеграла
у
у=f(x)
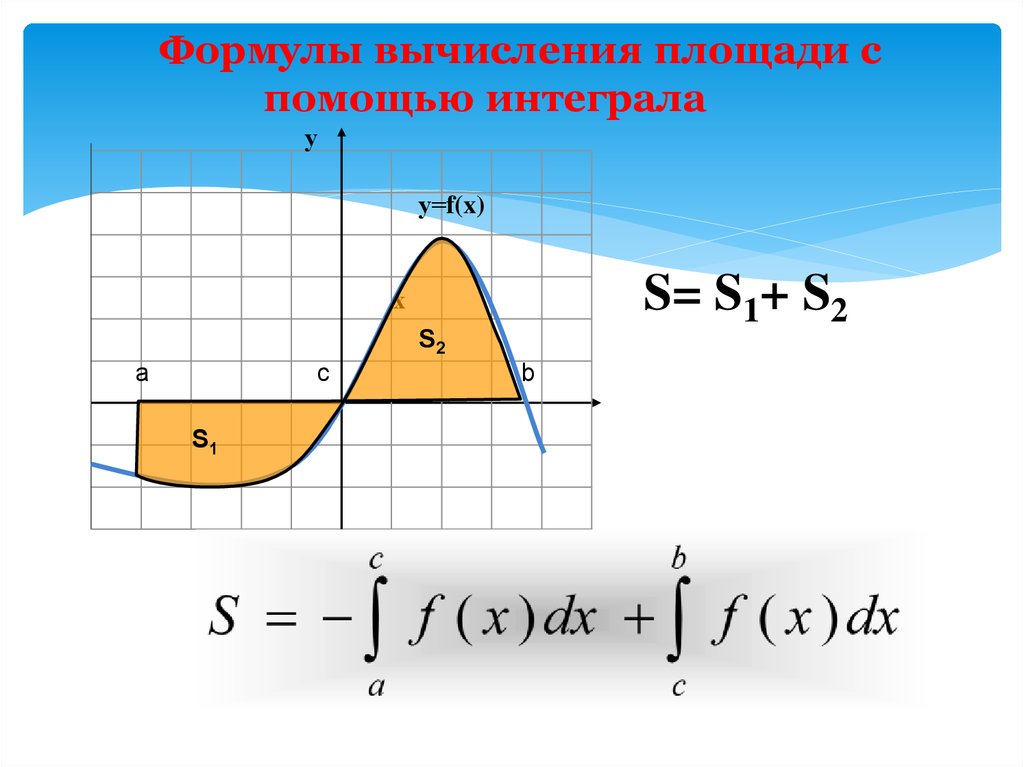
S= S1+ S2
х
S2
a
c
S1
b
15.
Формулы вычисления площади спомощью интеграла
у
y=f(x)
y=g(x)
x
a
b
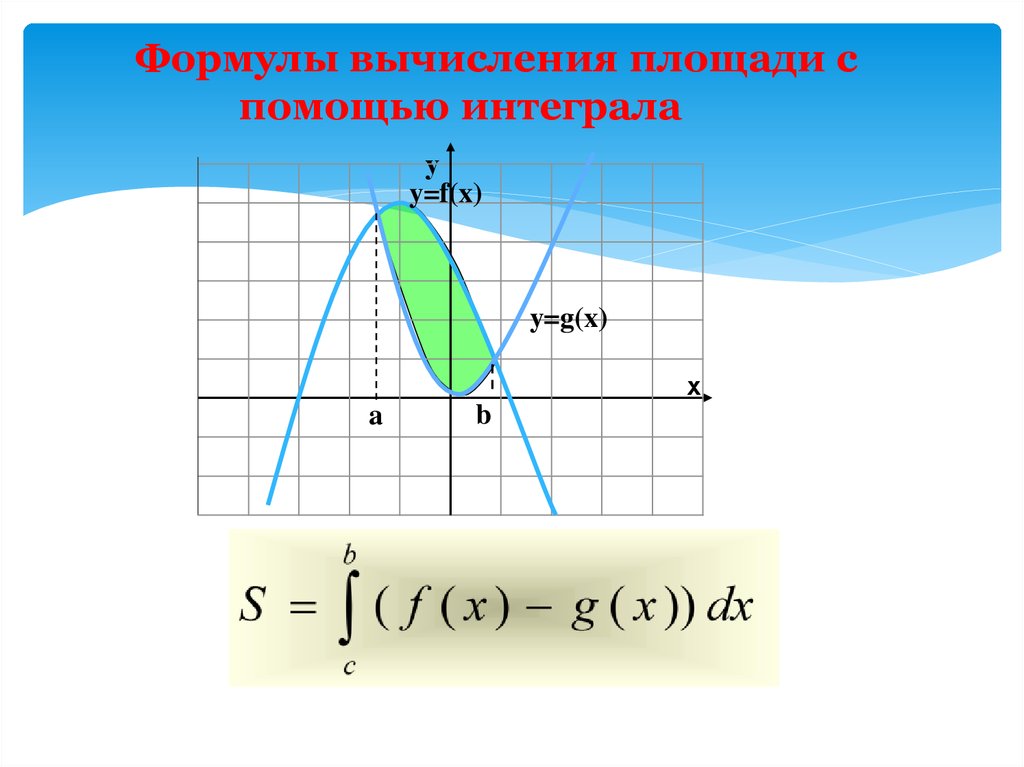
16.
Найдите площадь фигуры, ограниченной линиямиу = х2 + 2, х = 1, х = -2
у
1
S ( x 2)dx
у = х2 + 2
2
2
3
x
1
S ( 2 x) 2
3
х = -2
х=1
х
-2
1
8
S 2 ( 4)
3
3
S = 9 ед.кв
0
1
17.
Найдите площадь фигуры, ограниченной линиямиу = х - 3, у = х2 -3
у
х
-2
5
S 11
6
3
у = х2 - 3
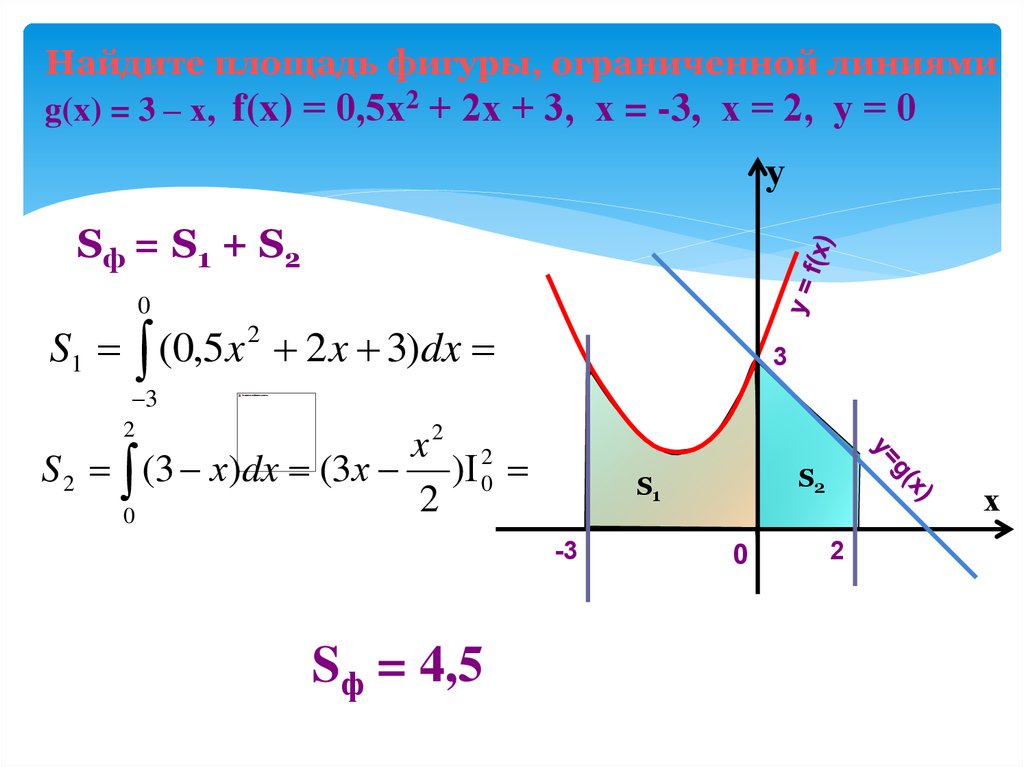
18.
Найдите площадь фигуры, ограниченной линиямиg(x) = 3 – х, f(x) = 0,5х2 + 2х + 3, х = -3, х = 2, у = 0
у
Sф = S1 + S2
0
S1 (0,5x 2 2 x 3)dx
3
3
2
x2 2
S 2 (3 х)dx (3х ) 0
2
0
-3
Sф = 4,5
S2
S1
0
х
2
19.
Запишите формулы для вычисленияплощади фигуры.
y
y
y= f(x)
y= g(x)
x
-4
0
y
y
y= f(x)
y= g(x)
x
y= f(x)
-4
x
-2
2
-4
x
2
20.
Запишите формулы для вычисленияплощади фигуры.
y
y
y= f(x)
y= g(x)
y= g(x)
x
-3
0
3
x
-2
0
3
21. Вычислить площадь фигуры, ограниченной линиями
Вариант 1Вариант 2
а) f(x) = 2x +1
б) f(x) =х2
а) f(x) = 1-х
б) f(x)= х2
y = 0, x = 0, x = 3
y = 0, x = 2, x = 4
Сделать проверку, используя любой другой
известный способ.










 Математика
Математика








