Площадь криволинейной трапеции

1.

Негосударственное образовательное учреждение
высшего профессионального образования
«Московский институт современного академического
образования»
Федеральный институт повышения квалификации и переподготовки
Факультет дополнительного профессионального образования
ПРЕЗЕНТАЦИЯ К УРОКУ
Тема: Площадь криволинейной трапеции
Предмет: алгебра и начала анализа
Класс: 11
Выполнил:
Слушатель факультета ДПО
Годунова Н.В.
учитель математики
г. Москва, 2016 г.

2. «Площадь криволинейной трапеции»

3.

Проверка домашнего задания

4.

Тест
Первообразная и определенный интеграл
А1. Выберите первообразную для функции f ( x) 4 х 1 .
2
2
2
1) F ( x) 16 х x 2) F ( x) 2 х
3) F ( x) 2 х x 1
2
4) F ( x) 16 х
А2. Какая из данных функций не является первообразной для функции
f ( x) sin 2 x ?
1
2
1) F ( x) cos 2 x
1
2
2) F ( x) 2 cos 2 x
1
2
3) F ( x) 2 cos 2 x 4) F ( x) 4 cos 2 x
А3. Найдите общий вид первообразных для функции f ( x) 5 .
1) 5x C
2) 5x
3) 5 C
4) 5x C
А4. Вычислите интеграл
cos xdx .
1)
2) 0
3) 1
4) 2
2
7
2) 0
3)
1
7
4) 1
0
1
А5. Вычислите интеграл
6
x
dx .
1
1)

5.

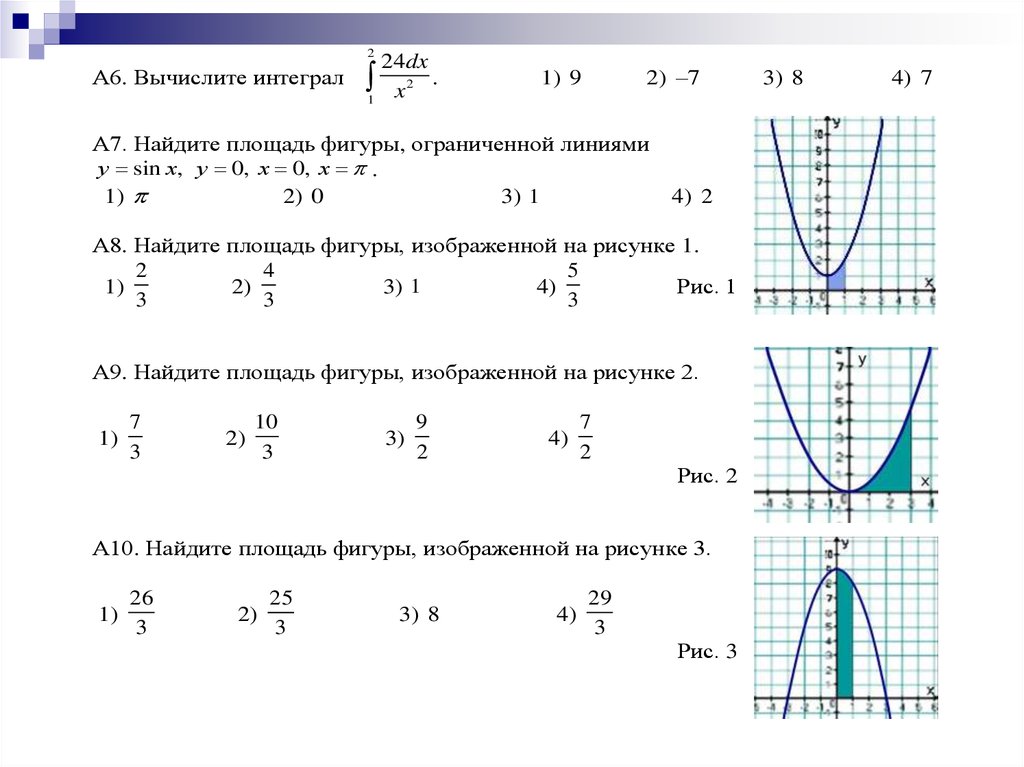
2
А6. Вычислите интеграл
1
24dx
.
x2
2) 7
1) 9
А7. Найдите площадь фигуры, ограниченной линиями
у sin x, y 0, x 0, x .
1)
2) 0
3) 1
4) 2
А8. Найдите площадь фигуры, изображенной на рисунке 1.
2
4
5
1)
2)
3) 1
4)
Рис. 1
3
3
3
А9. Найдите площадь фигуры, изображенной на рисунке 2.
1)
7
3
2)
10
3
3)
9
2
4)
7
2
Рис. 2
А10. Найдите площадь фигуры, изображенной на рисунке 3.
1)
26
3
2)
25
3
3) 8
4)
29
3
Рис. 3
3) 8
4) 7

6. Ответы на тест

А1
А2
А3
А4
А5
А6
А7
А8
А9
А10
3
3
1
2
1
4
4
2
3
1

7. Найти первообразную функции:

а ) f ( x) 2 sin x 3 cos x
3
б ) f ( x)
x2
x
в ) f ( x) 4 x 3 6 x
г ) f ( x) 7
1
д) f ( x ) 1
2
cos x
на (0; )

8. «Площадь криволинейной трапеции»

Тема урока:
«Площадь
криволинейной
трапеции»

9.

y
у = f(x)
0
а
в
х
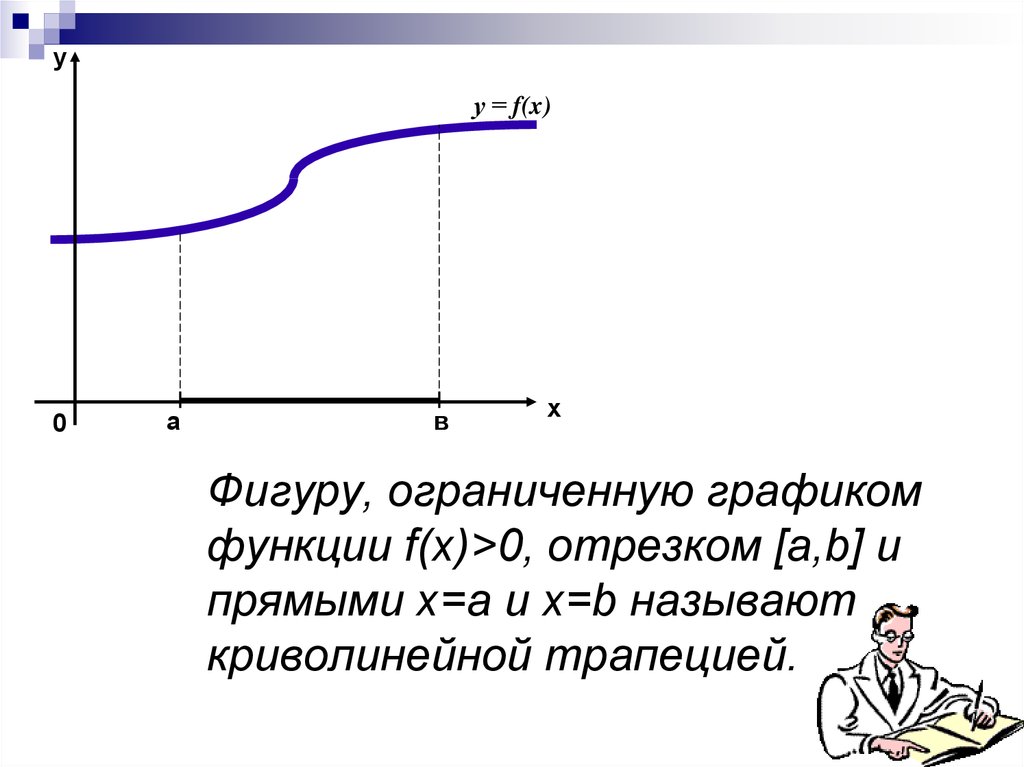
Фигуру, ограниченную графиком
функции f(x)>0, отрезком [a,b] и
прямыми х=а и х=b называют
криволинейной трапецией.

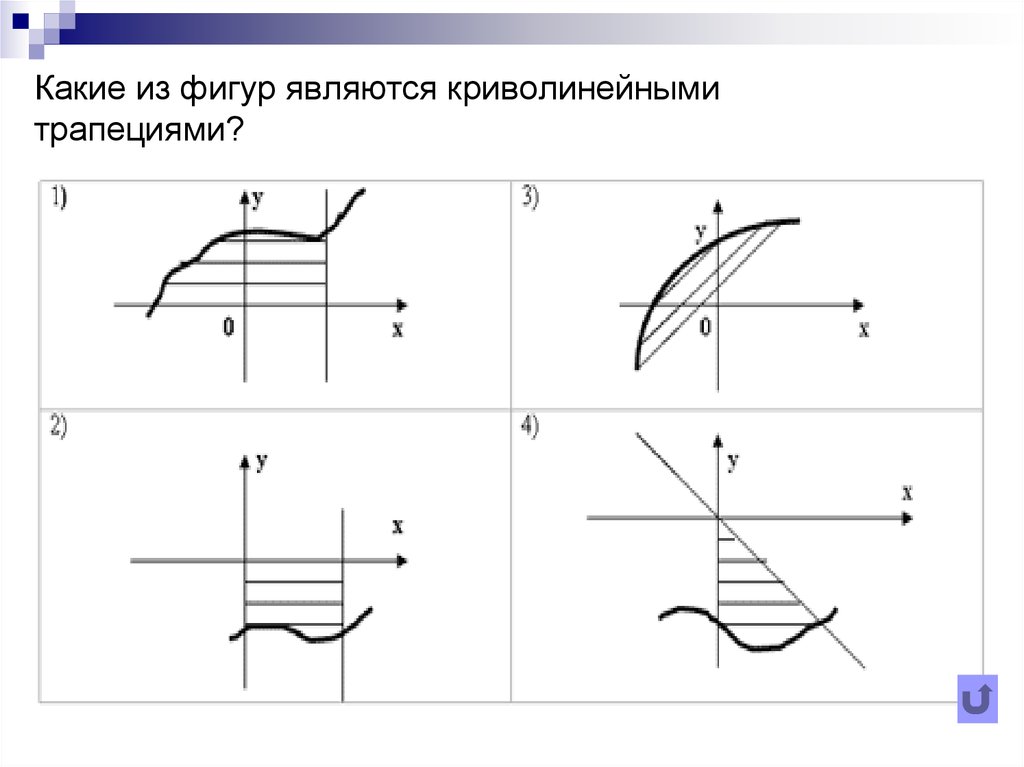
10. Какие из фигур являются криволинейными трапециями?

11.

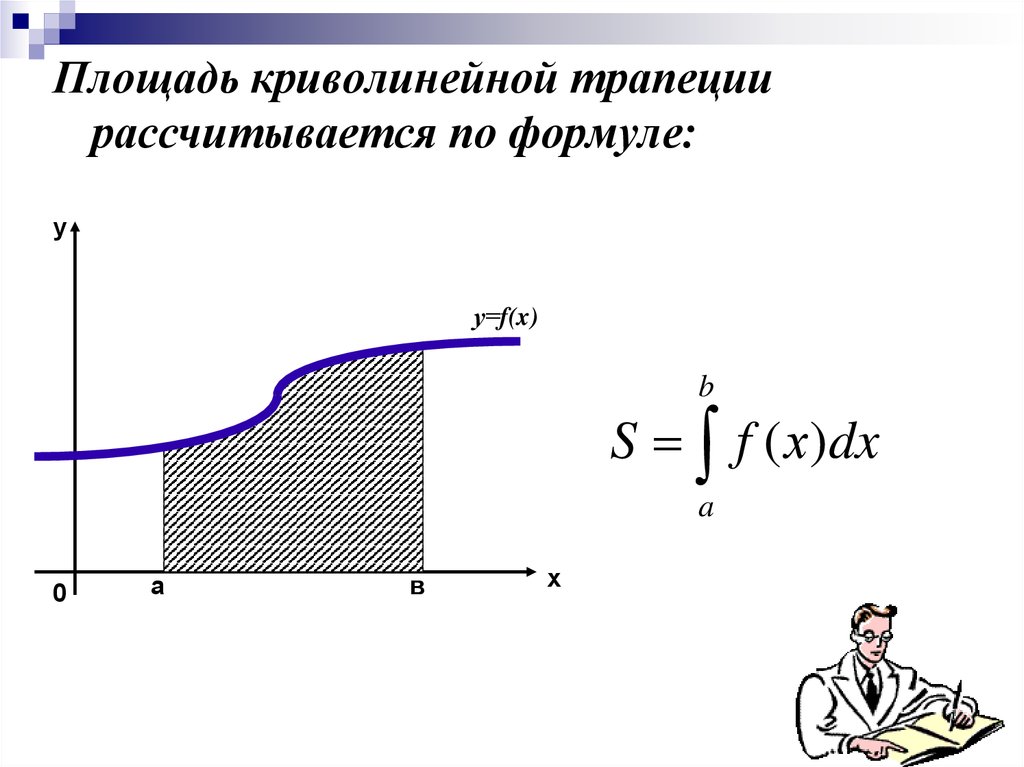
Площадь криволинейной трапеции
рассчитывается по формуле:
y
у=f(x)
b
S f ( х)dx
a
0
а
в
х

12. Фигура ограничена графиком функции у=f(x), отрезком [a, в] и прямыми х=а, х=в. Как можно определить ее площадь?

y
а
х
у=f(x)
0

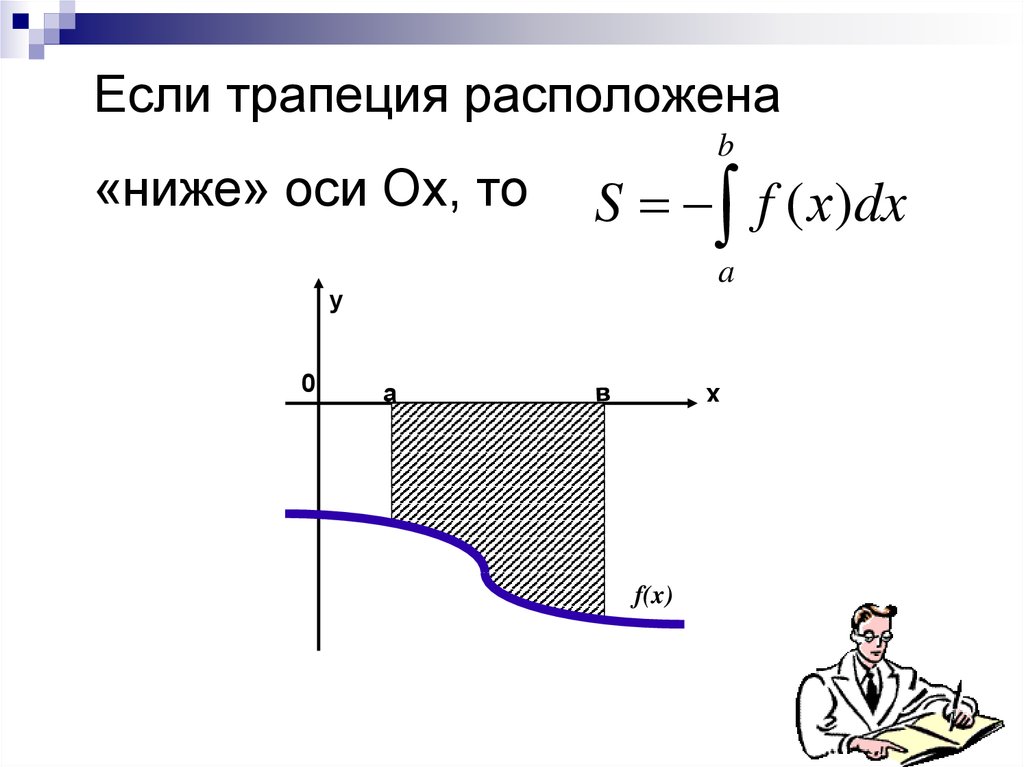
13. Если трапеция расположена «ниже» оси Ох, то

b
S f ( х)dx
a
y
а
х
f(x)
0

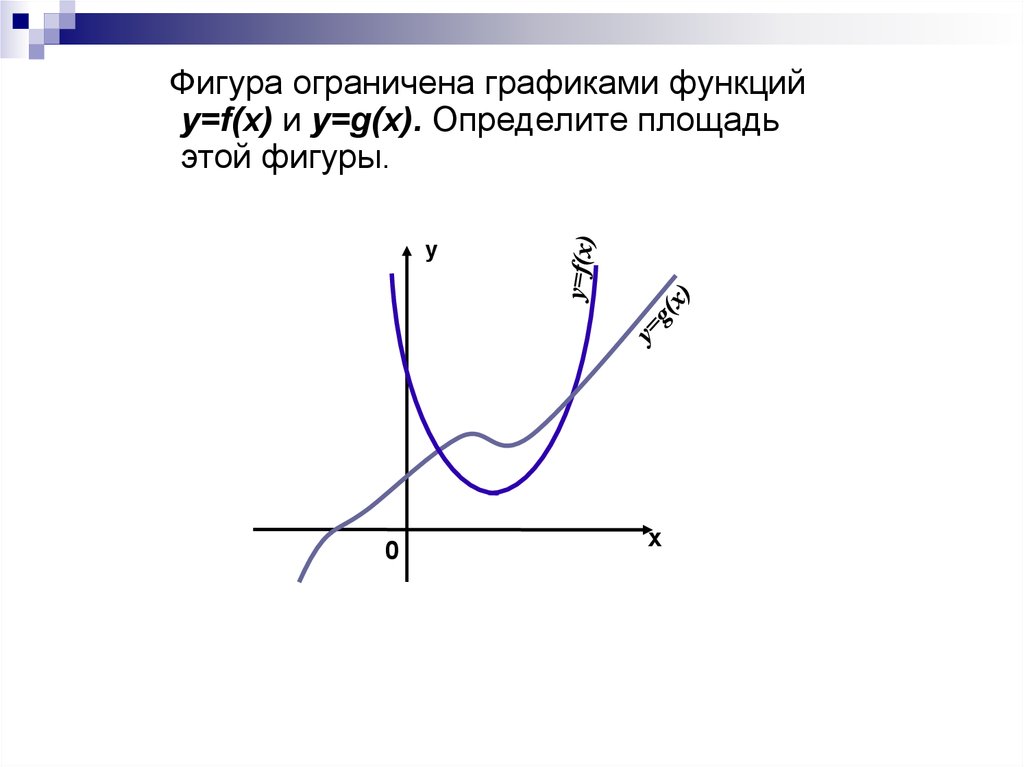
14.

Фигура ограничена графиками функций
у=f(x) и у=g(х). Определите площадь
этой фигуры.
y
0
х

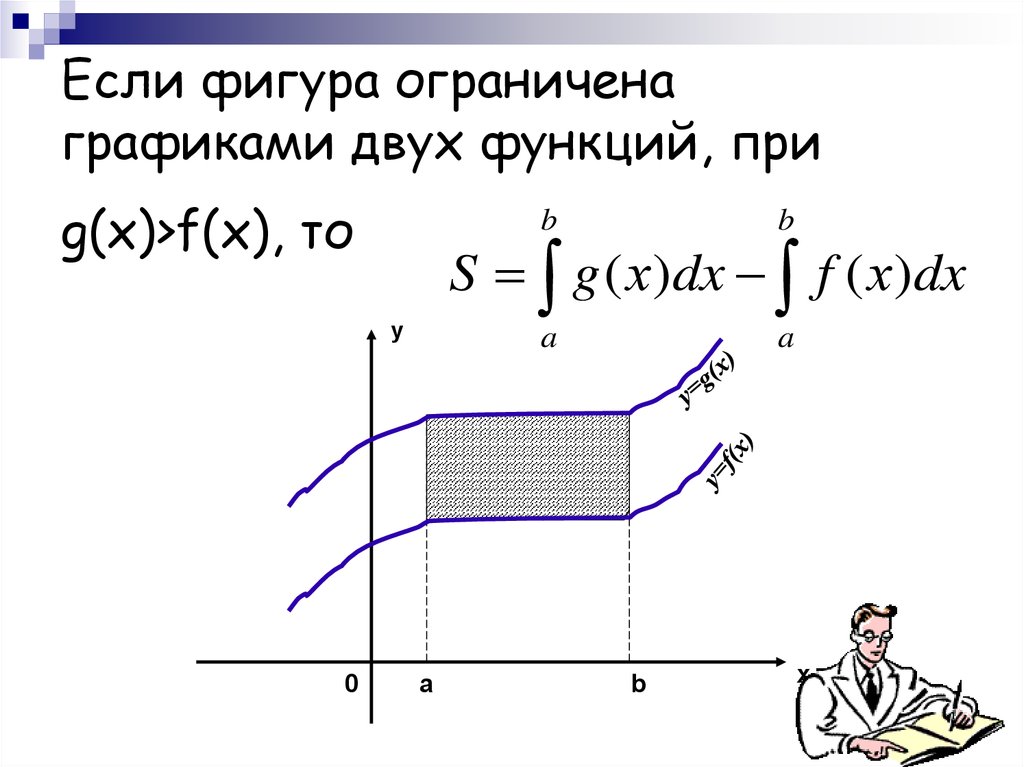
15.

Если фигура ограничена
графиками двух функций, при
g(х)>f(х), то
b
a
a
S g ( х)dx f ( х)dx
y
0
b
a
b
х

16.

Определите площади фигур, ограниченных линиями.
у=f(х), у=g(х), ось Ох
у=f(х)
y
y
у=f(х)
у=f(х)
C
0
A
0
B
х
А х

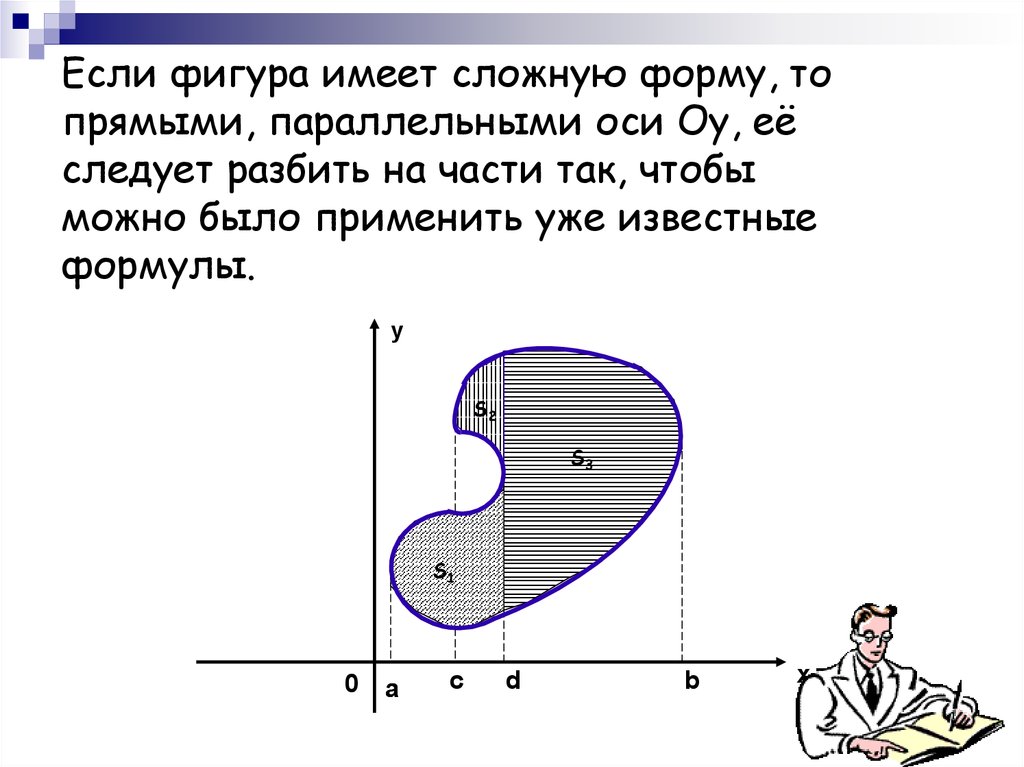
17.

Если фигура имеет сложную форму, то
прямыми, параллельными оси Оу, её
следует разбить на части так, чтобы
можно было применить уже известные
формулы.
y
S2
S3
S1
0 a
с
d
b
х

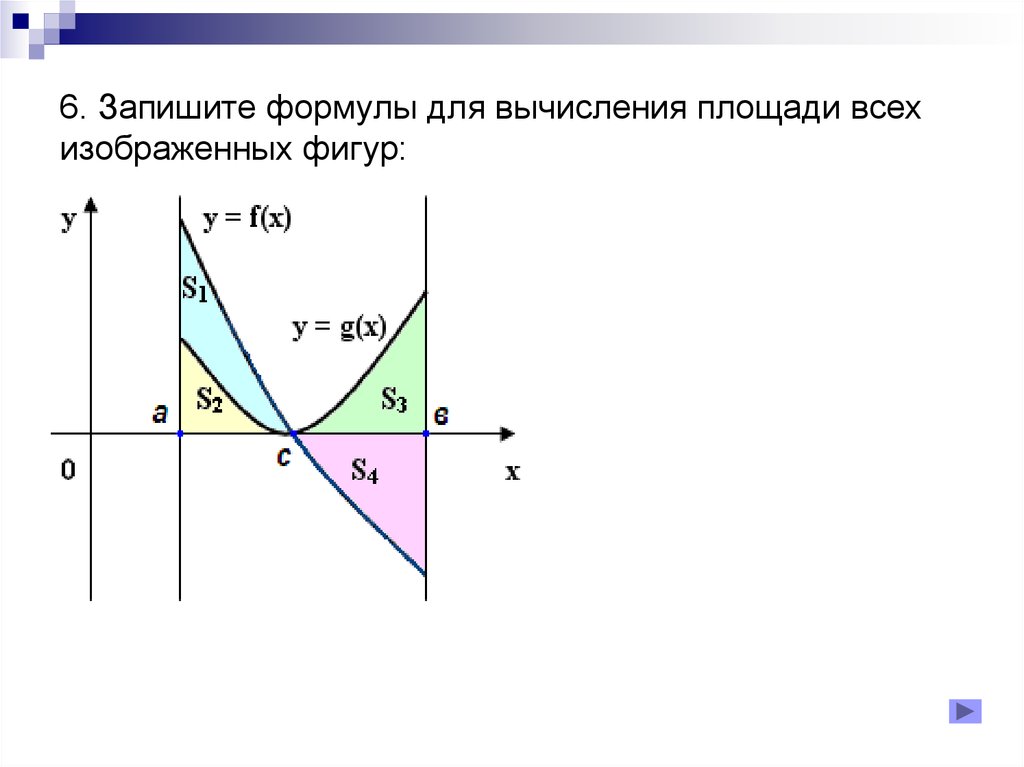
18. 6. Запишите формулы для вычисления площади всех изображенных фигур:

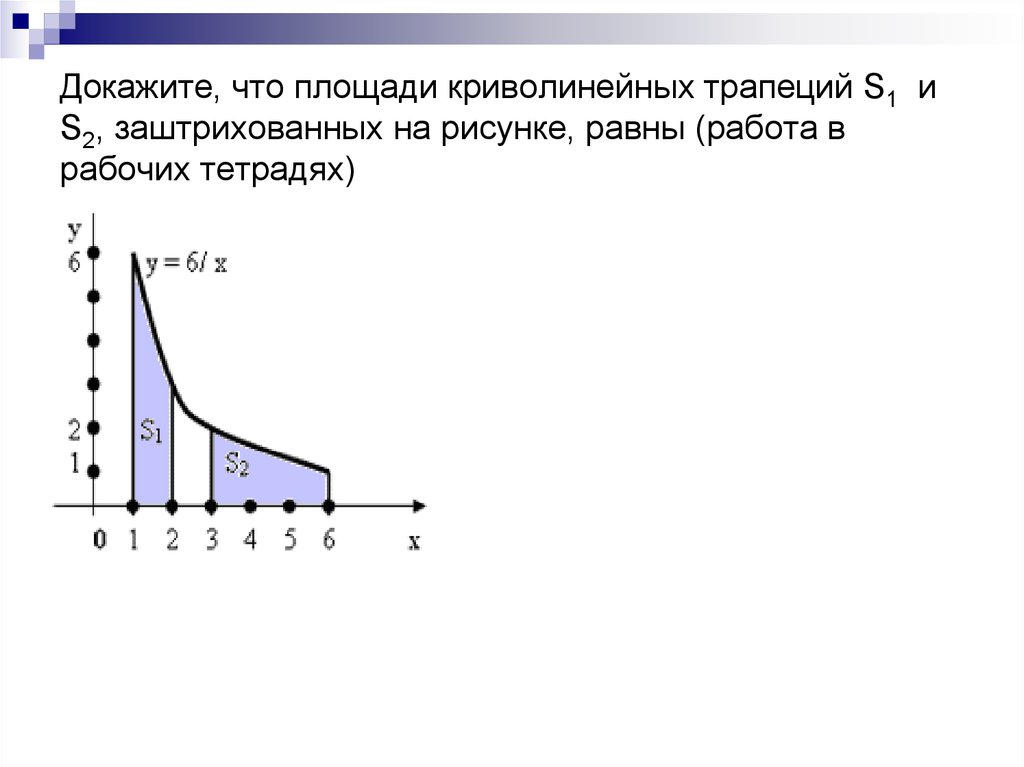
19. Докажите, что площади криволинейных трапеций S1 и S2, заштрихованных на рисунке, равны (работа в рабочих тетрадях)

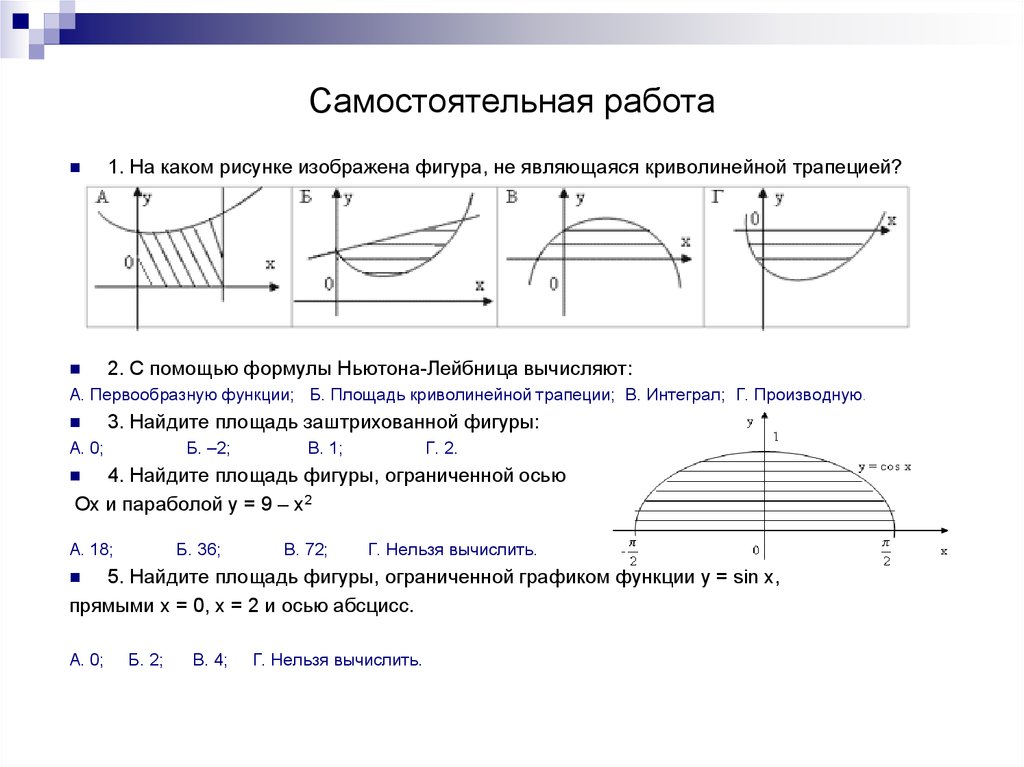
20. Самостоятельная работа

1. На каком рисунке изображена фигура, не являющаяся криволинейной трапецией?
2. С помощью формулы Ньютона-Лейбница вычисляют:
А. Первообразную функции; Б. Площадь криволинейной трапеции; В. Интеграл; Г. Производную.
3. Найдите площадь заштрихованной фигуры:
А. 0;
Б. –2;
В. 1;
Г. 2.
4. Найдите площадь фигуры, ограниченной осью
Ох и параболой у = 9 – х2
А. 18;
Б. 36;
В. 72;
Г. Нельзя вычислить.
5. Найдите площадь фигуры, ограниченной графиком функции у = sin x,
прямыми х = 0, х = 2 и осью абсцисс.
А. 0;
Б. 2;
В. 4;
Г. Нельзя вычислить.

21. Ответы к самостоятельной работе

Ответы к
1. Б; Г
2. Б,В;
3. Г;
4. Б;
5. В.
самостоятельной
работе

22. Итоги урока, домашнее задание

Площадь криволинейной трапеции вычисляется с
помощью определенного интеграла. Определенный
интеграл вычисляется с помощью формулы
Ньютона-Лейбница (если удается найти
первообразную) или с помощью интегральных сумм
(если не удается найти первообразную).
Д/З: № 49.15(а) 49.11(б) 49.23(а)
Дополнительное задание:
Найти в Интернете примеры практического
применения вычисления площади криволинейной
трапеции