Похожие презентации:
Способы отбора корней
1.
3а). Решите уравнение 2 cos 2 х 4 sin
х 1 0
2
2
2
cos 2 x cos x sin x
б). Найдите все корни этого уравнения, принадлежащие отрезку 3 ;
Применим формулу приведения:
2 cos 2х 4 cos х 1 0
Название «синус» изменится на
VI чет.
«косинус», т.к.
2
2
sin2 хx 41cos
cos
2 cos 2 х sin
х 1x 0
2 cos 2 х 2 sin 2 x 4 cos х 1 0
3
sin
x – cos х
2
В VI чет. знак исходной функции
синуса отрицательный
2 cos 2 х 2 1 cos 2 х 4 cos х 1 0
2
4
a
4a1
2 cos х 2 2 cos х 4 cos
х
30 0
2
2
2
D
4
1х 3 0
1 4 4 ( 32) 64
4 cosarccos
х 4 cos
arccos
12
Нам будет2удобно 3
3
1 2
a
1;1
cos х
записать решение в 1
4
8
8
2
виде a
двух
множеств.
2 1
1
2 4
х arccos
2 n; 2 n
a2
3
2
2
2
2.
Найдите все корни этого уравнения, принадлежащие отрезку 3 ;2
n=-1 x x
2 n
2
3
2 n
3
3 ;
2
3 2n 1
3
2
2
3 2n 1
3
3
11
5
2n
3
3
11
5
n
6
6
n 1,
:
4
x
3
2
3
:2
2
2 n
3
3 ;
n=-1
2
3 2n 1 2
3
3
1
1
2 2n
3
3
7
1
:2
2n
3
3
7
1
n
6
6
n 1,
82
3
xx
2 ,
33
:
3.
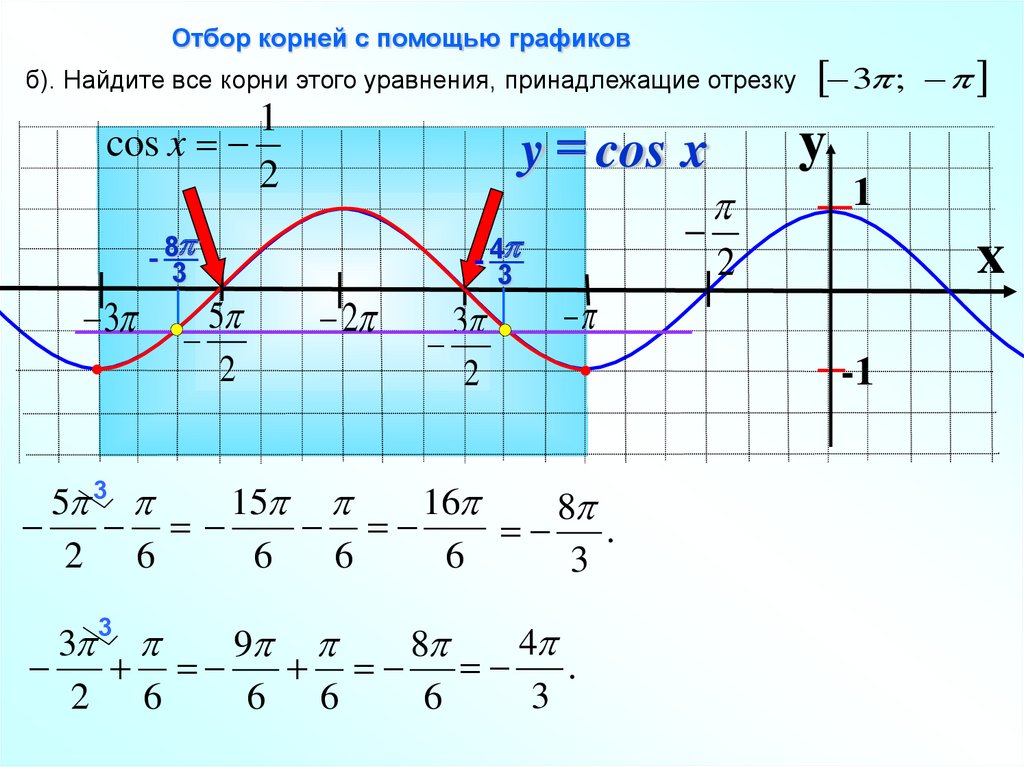
Отбор корней с помощью графиковб). Найдите все корни этого уравнения, принадлежащие отрезку
1
cos x
2
3
- 8
3
5
2
y cos x
2
- 4
3
3
2
2
4
3
9
8
.
3
2 6
6 6
6
y
1
x
5 3
15
16
8
.
2 6
6
6
6
3
3
3 ;
-1
4.
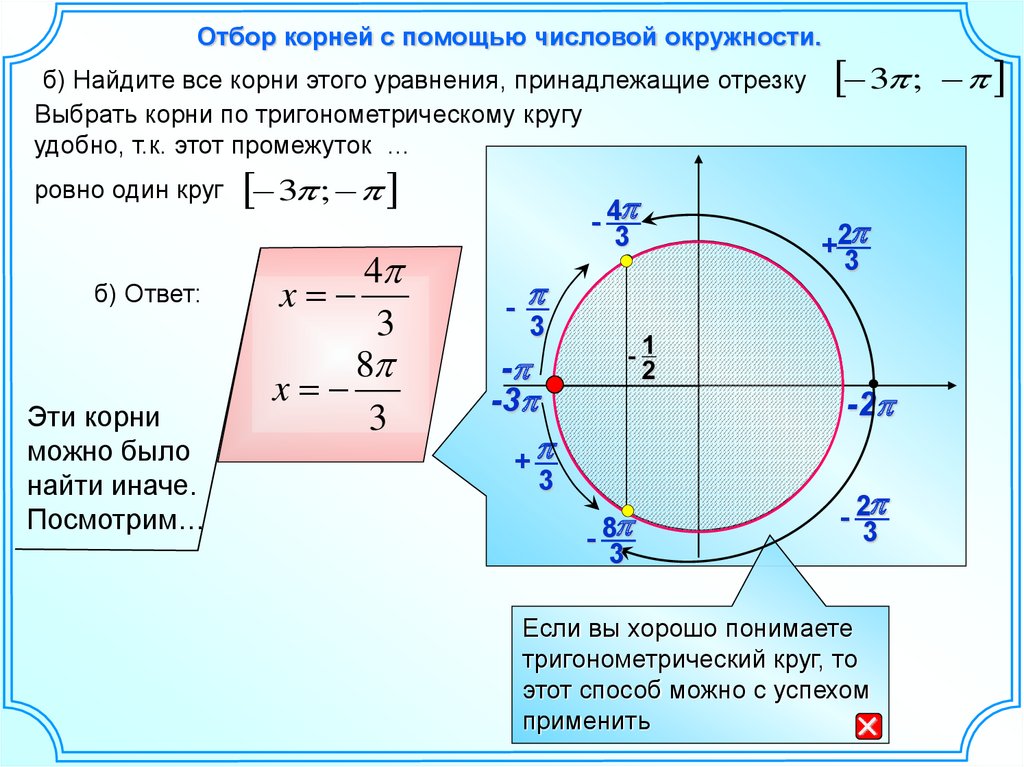
Отбор корней с помощью числовой окружности.б) Найдите все корни этого уравнения, принадлежащие отрезку
Выбрать корни по тригонометрическому кругу
удобно, т.к. этот промежуток …
ровно один круг
б) Ответ:
Эти корни
можно было
найти иначе.
Посмотрим…
3 ;
4
x
3
8
x
3
- 4
3
-
3
-
-3
-1
2
+
3
- 8
3
3 ;
+2
3
-2
- 2
3
Если вы хорошо понимаете
тригонометрический круг, то
этот способ можно с успехом
применить


 Математика
Математика








