Похожие презентации:
Тригонометрические уравнения
1.
2.
Верно ли, что:1
а ) arccos ;
2 3
1
в ) arccos( ) ;
2
3
2
б ) arcsin(
) ;
2
4
3 11
г ) arccos
;
2
6
2
3
д) arccos(
)
. е)arctg 3 .
3
2
4
3.
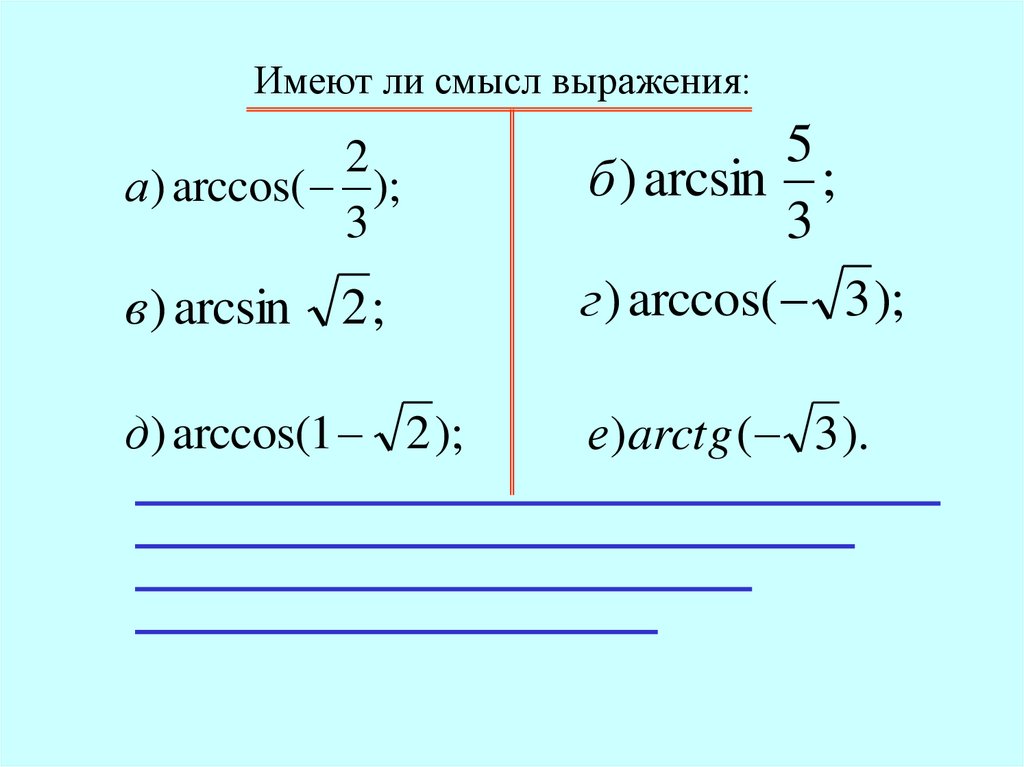
Имеют ли смысл выражения:в ) arcsin 2 ;
5
б ) arcsin ;
3
г ) arccos( 3 );
д) arccos(1 2 );
е)arctg ( 3 ).
2
а ) arccos( );
3
4.
Решить уравнение:1
а ) sin x ;
2
k
x ( 1)
k, k Z.
6
в ) 2сosx 1 0;
x
4
2 k , k Z .
3
б ) cos x
;
2
x
6
2 k , k Z .
г )tg 2 x 1;
x
8
k
2
, k Z.
5.
Пример 1. Решить уравнение2 sin2x + sinx - 1 = 0.
Решение.
Введём новую переменную t = sinx. Тогда данное
уравнение примет вид
2t2 + t - 1 = 0.
Решим его: D = 1 + 8 = 9,
1 3 1
t1
,
4
2
1 3
t2
1 .
4
Cледовательно,
sinx = 1/2
или
sinx = -1.
6.
1) sinx = 1/2,1
х ( 1) arcsin k , k Z ,
2
k
x ( 1)
k
6
k, k Z.
2) sinx = -1,
х
2
2 n, n Z .
Ответ : ( 1)
k
6
k, k Z ,
2
2 n, n Z .
7.
Пример 2. Решить уравнение6sin2x + 5 cosx - 2 = 0.
Решение.
Заменяя sin2x на 1-сos2x, получим
квадратное уравнение относительно сosx.
6 ( 1-cos2x ) + 5 cosx - 2 = 0,
-6 cos2x + 5cosx + 4 = 0,
6 cos2x - 5cosx - 4 = 0.
Пусть cos x = t, тогда
t1= - 1/2, t2 = 4/3.
6t2 - 5t - 4 = 0,
8.
Cледовательно, сos x = - 1/2 или cos x = 4/3.Решая уравнение сos x = -1/2, находим:
2
х
2 k , k Z .
3
Уравнение cos x = 4/3 не имеет
решений, так как 4/3 > 1.
2
Ответ :
2 k , k Z .
3
9.
Пример 3. Решить уравнениеРешение.
tgx + 2ctgx = 3.
1
,
Поскольку ctgx =
tgx
то уравнение можно записать в виде:
2
tgx
3.
tgx
Обозначим tgx через t. Получим
уравнение t 2 3,
t
которое приводится к квадратному
(t 0)
- 3t + 2 = 0,
t2
10.
t2 - 3t + 2 = 0.По теореме, обратной теореме Виета,
t1 = 2,
t2=1.
1)tgx 2,
x arctg 2 n, n Z .
2)tgx 1,
x arctg1 k , k Z ,
x
k, k Z.
4
Ответ : arctg 2 n, n Z ,
k, k Z.
4
11.
Пример 4.sin2 4x = 1/4
Решение.
1 cos 2 x
1
;
2
4
cos 2x =1/2
Х= ±π/6 + πn; n Є Ζ
12.
Пример 5. 3 sin x +4 cos x =0;Решение.
Поделим обе части уравнения на cos x ≠ 0.
3 tg x + 4 =0 ;
tg x = -4/3 ;
Ответ : arctg (4 / 3) k , k Z .




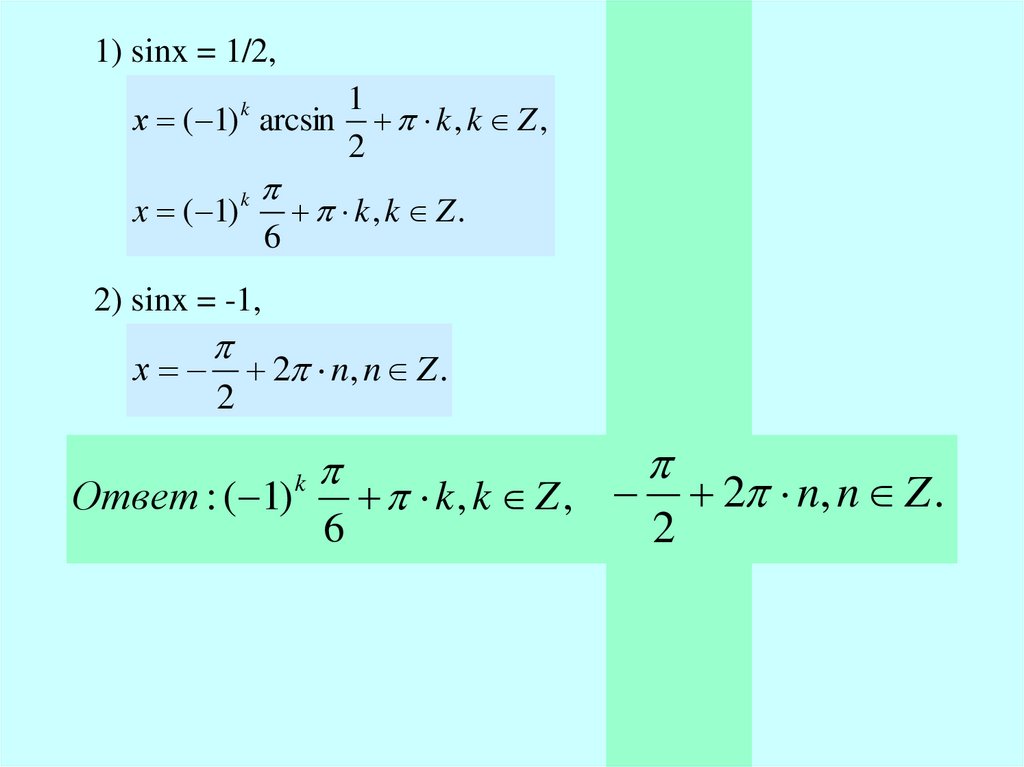






 Математика
Математика








