Похожие презентации:
Симплекс-метод. Тема 4
1.
Симплекс-методТЕМА 4
НТУУ КПІ ФІОТ АСОІУ ДО-1 Олена Жданова
2020
2.
ТЕМА 4. Симплекс-метод (СМ)4.1
4.2
4.3
4.4
4.5
4.6
Ідея симплекс – методу
Перетворена задача
Спосіб переходу від одного ДБР до іншого
Умова оптимальності ДБР
Схема симплекс – методу
Збіжність симплекс – методу
3.
Основні визначення та теореми ЛП(з Теми 3)
4.
Теорема про оптимальність вершинибагатогранника
Маємо ЗЛП:
c x max ,
x X .
Теорема. Нехай допустима множина X задачі
ЛП є багатогранником. Тоді ЦФ c T x досягає
свого максимуму у вершині X .
Якщо функція c T x набуває максимального
значення більш ніж в одній точці, то вона
досягає того ж значення в будь-якій точці, що є
їх опуклою лінійною комбінацією.
T
5.
Базисні розв’язки(Алгебраїчне представлення вершин)
a*1 x1 a*2 x2 a*n xn b
Визначення. Базисом ß матриці А називається набір з
m лінійно незалежних стовпців ß a* j1 , a* j 2 , , a* j m .
Визначення. Базисною матрицею називається m m
– матриця, складена із стовпців, що входять в базис ß :
a* j1 a* j2 a* j m .
Визначення. Базисним розв’язком, відповідним базису
ß , називається вектор x R n у якому
– x j 0 при a* j ß ;
– x j k є k -й компонент вектора 1b , де k 1, m .
6.
Процедура знаходження базисних розв’язків (БР)1) Вибрати множину ß , що складається з m лінійно
незалежних стовпців матриці A .
2) Покласти рівними 0 всі компоненти вектора x які
відповідні стовпцям, що не входять в ß . Ці змінні
називатимемо небазисними (їх n m ) .
3) Розв’язати m отриманих рівнянь для визначення тих
компонент вектора x , що залишилися. Вони
називатимуться базисними змінними (їх m )
7.
Допустимі базисні розв’язки (ДБР)Визначення. Розв’язок

























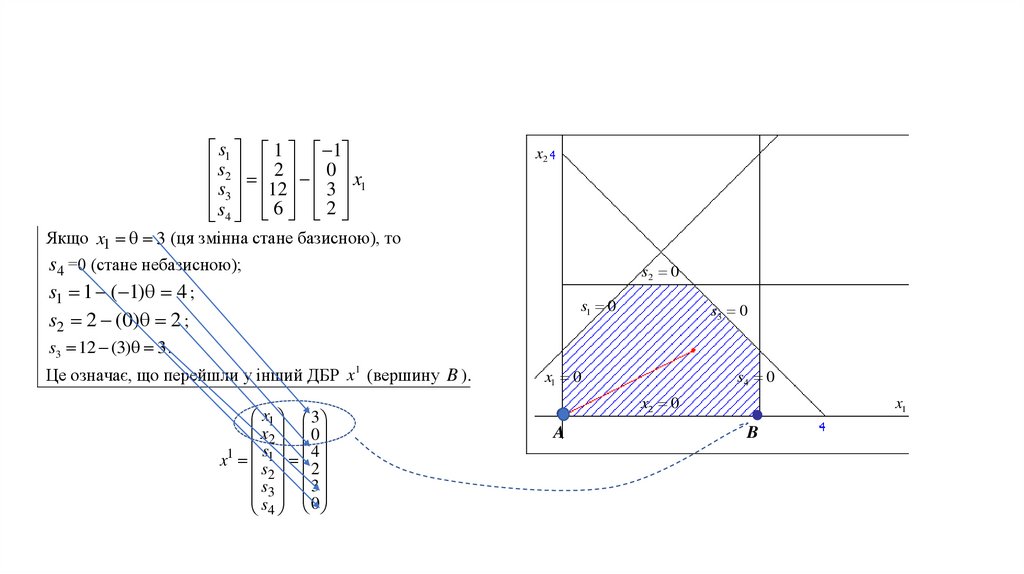






















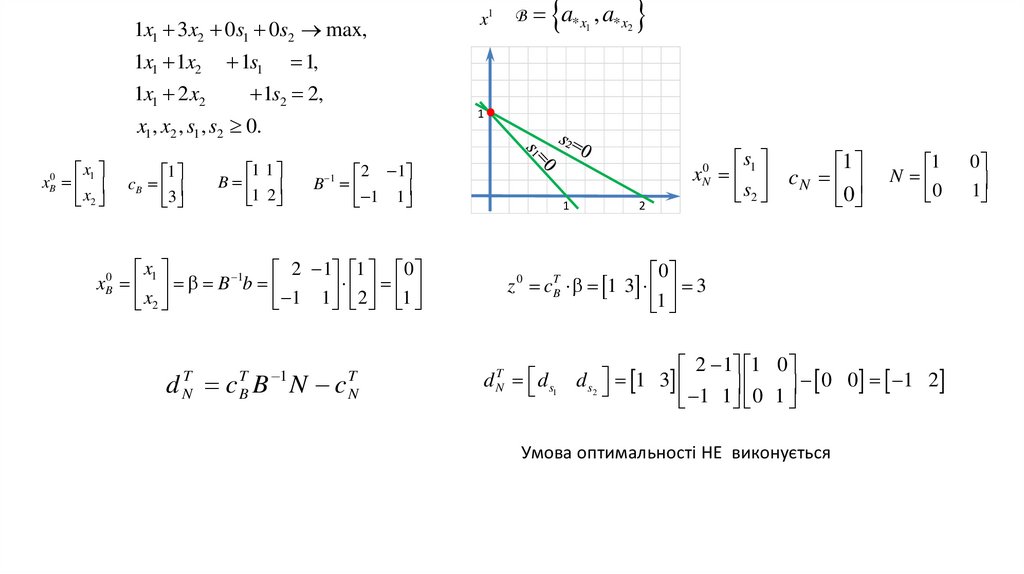










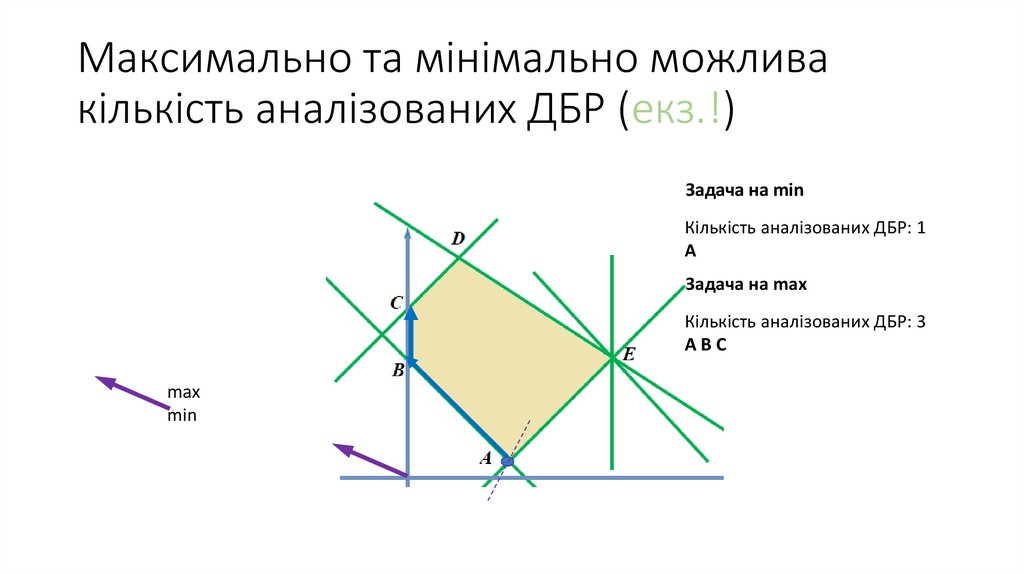








 Математика
Математика








