Похожие презентации:
Векторні величини. Метод координат
1. Тема 2. Векторна алгебра
Лекція 5.Векторні величини.
Метод координат.
2. План
Лінійні операції над векторамиПроекція вектора на вісь
Лінійна залежність та
незалежність векторів
Метод координат
3.
Вектор – це впорядкована пара точок.В
А
компланарні
колінеарні
рівні
Відстань між початком і кінцем вектора
називається його довжиною, або модулем.
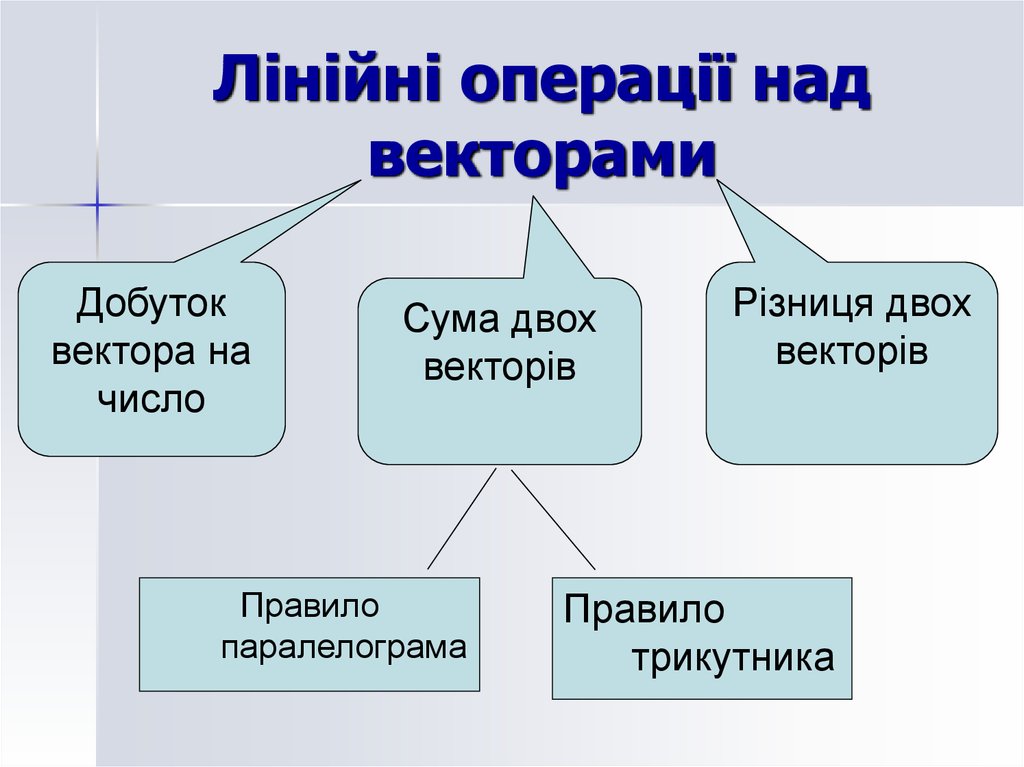
4. Лінійні операції над векторами
Добутоквектора на
число
Сума двох
векторів
Правило
паралелограма
Різниця двох
векторів
Правило
трикутника
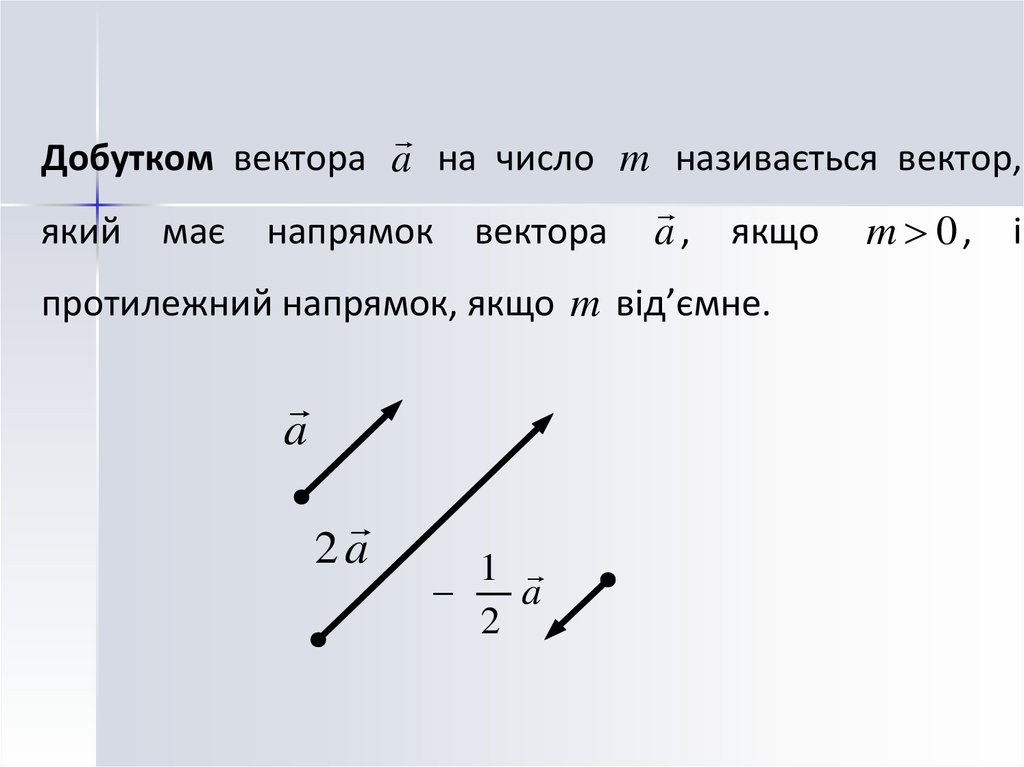
5.
Добутком вектора a на число m називається вектор,який має напрямок вектора a , якщо m 0 , і
протилежний напрямок, якщо m від’ємне.
a
2a
1
a
2
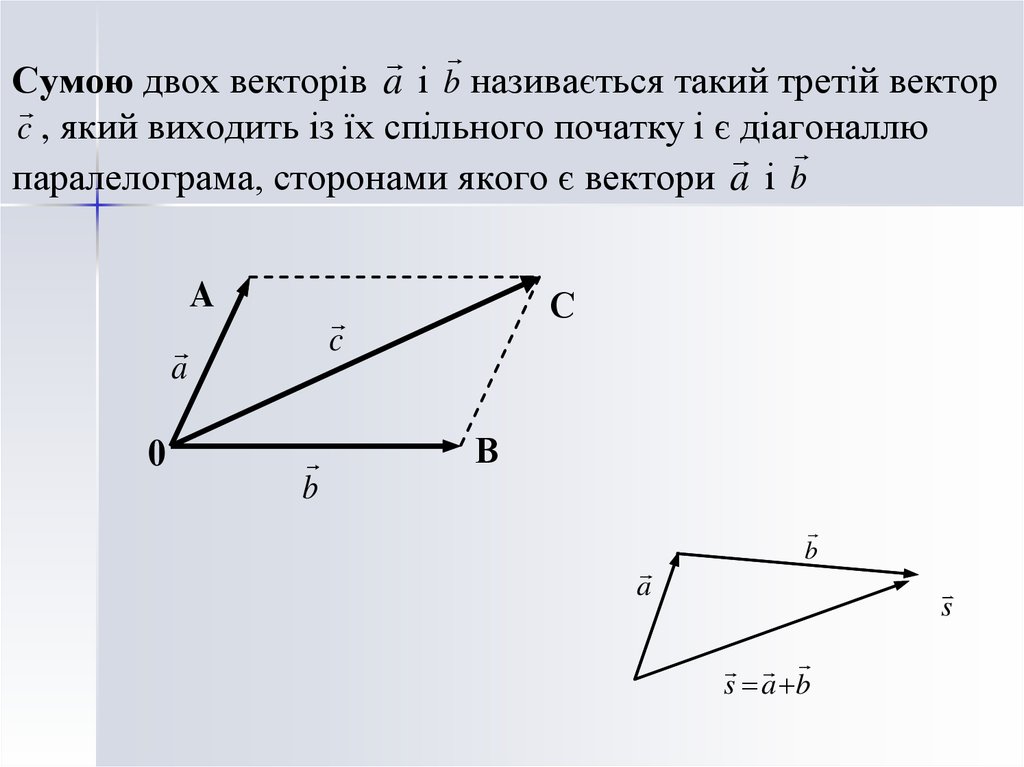
6.
Сумою двох векторів a і b називається такий третій векторc , який виходить із їх спільного початку і є діагоналлю
паралелограма, сторонами якого є вектори a і b
А
a
0
С
c
b
В
a
b
s
s a b
7. Властивості:
a b b a- комутативність;
- асоціативність;
a b c a b c
m a b ma mb дистрибутивність по відношенню до
множення на число
m n a ma na
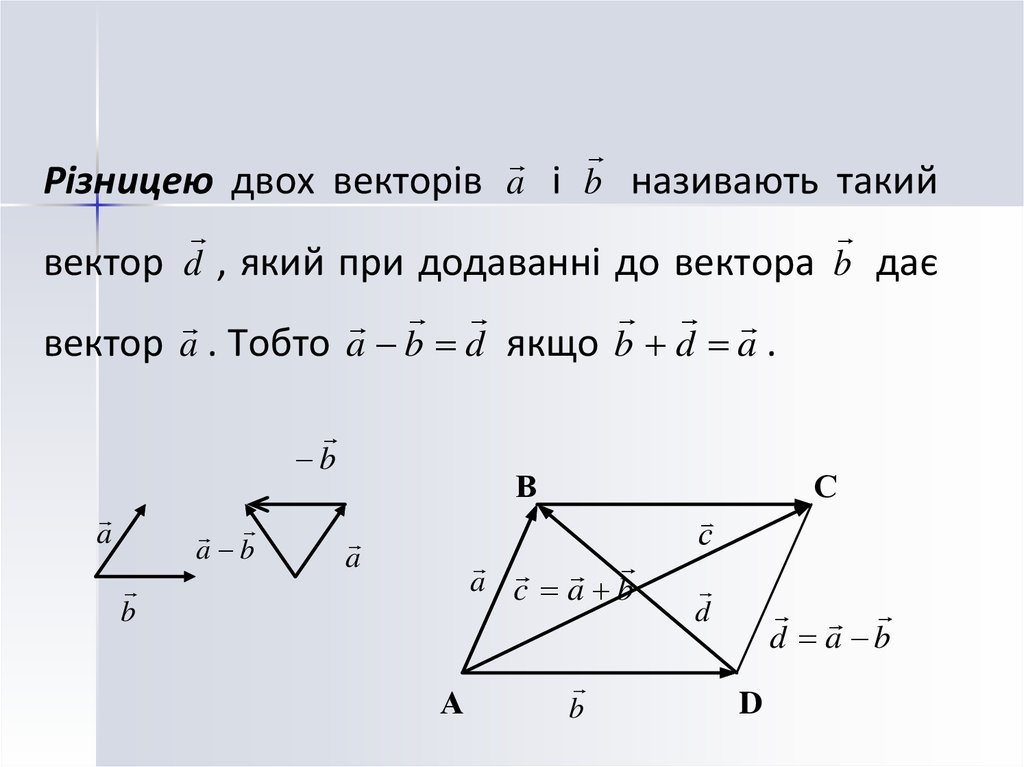
8.
Різницею двох векторів a і b називають такийвектор d , який при додаванні до вектора b дає
вектор a . Тобто a b d якщо b d a .
b
a
a b
b
В
a
a c a b
А
b
С
с
d
d a b
D
9. Проекція вектора на вісь
Проекцією вектора AB на вісь називається довжинавідрізка ab цієї осі, що міститься між основами проекцій
початку і кінця вектора AB на вісь .
В
А
a
b
npe
AB AB cos
10. Властивості :
рівні вектори мають рівні проекції;при множенні вектора AB на число m
його проекція на вісь також множиться на
це ж саме число;
проекція суми двох векторів на вісь
дорівнює сумі проекцій цих векторів
11. Означення
Система векторів a1 , a 2 ,..., a m називаєтьсялінійно залежною, якщо існують такі сталі
c1 , c 2 ,...,c m , серед яких є хоча б одна відмінна
від нуля, і для яких виконується рівність
c1 a1 c 2 a 2 ... c m a m 0 .
12.
Теорема Якщо система векторів лінійнозалежна, то хоча би один з них можна
представити у вигляді лінійної комбінації
інших.
Теорема (обернена). Якщо один з векторів
даної системи можна представити у вигляді
лінійної комбінації інших, то така система
векторів лінійно залежна.
13. Означення
Система векторів a1 , a 2 ,..., a m називаєтьсялінійно незалежною, якщо рівність
c1 a1 c 2 a 2 ... c m a m 0 виконується тоді і
тільки тоді, коли усі сталі c i дорівнюють нулю
i 1,2,..., m .
14.
Теорема . Довільні два колінеарні векторилінійно залежні і, навпаки, два неколінеарних
вектори лінійно незалежні.
Теорема . Три компланарних вектори лінійно
залежні і, навпаки, три некомпланарних
вектори лінійно незалежні.
Теорема . Довільні три ненульові вектори на
площині є лінійно залежними.
Теорема . Довільні чотири вектори у просторі
лінійно залежні.
15.
Базисом на прямій називається будь-якийненульовий вектор на цій прямій.
Базисом на площині називаються два не
колінеарні вектори зі спільним початком
на цій площині, взяті в певному порядку.
Базисом в просторі називаються
довільні три не компланарні вектори,
які беруться в певній послідовності.
16. Теорема
e1 , e2 , e3Якщо вектори
утворюють
базис в просторі, то будь-який
вектор a цього простору може
бути представлений до того ж
єдиним
чином,
як
лінійна
комбінація векторів базису.
a 1e1 2 e2 3 e3 .
17. Теорема
e1e2
Якщо на площині вектори
та
утворюють базис, то будь-який з
ними компланарний вектор a можна
представити і при тому єдиним
чином як лінійну комбінацію
векторів базису.
a 1e1 2 e2 .
18. Означення
Якщоe1 , e 2 , e3 -
базис і вектор
a 1e1 2 e2 3 e3 ,
то числа 1 , 2 , 3
називаються координатами вектора
даному базисі.
aв
19. Декартова системи координат
Декартовою системоюкоординат в просторі називається
сукупність точки
e1 , e2 , e3 .
O
та базису
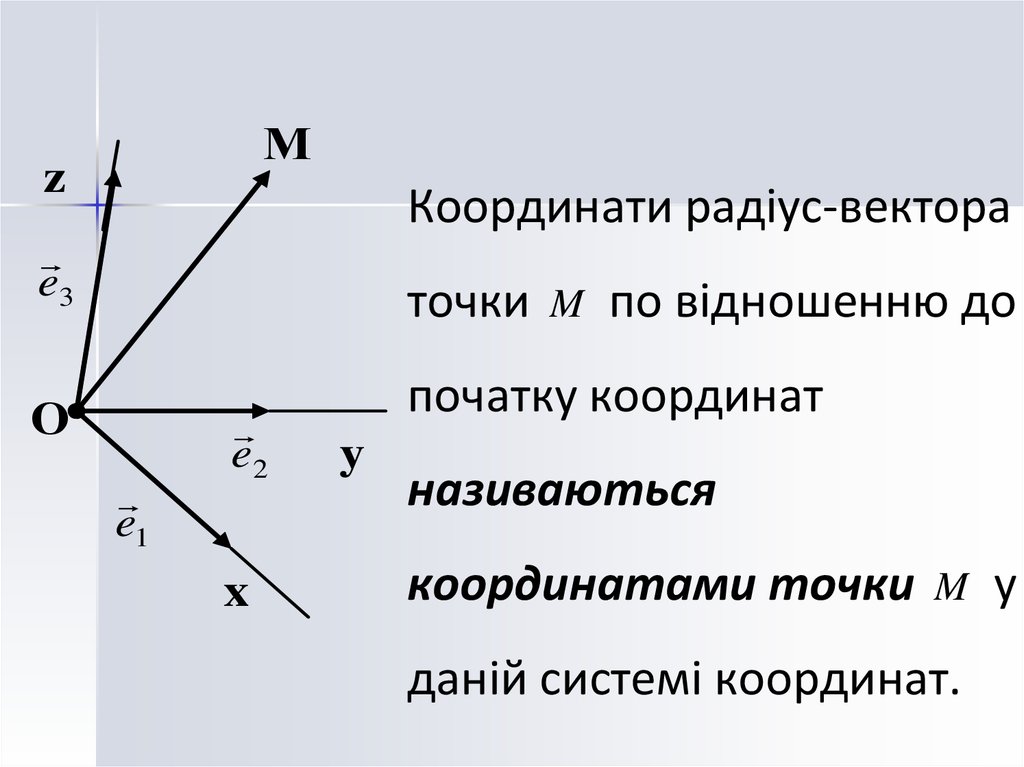
20.
Мz
Координати радіус-вектора
e3
точки
О
e1
e2
x
M
по відношенню до
початку координат
y
називаються
координатами точки
M
даній системі координат.
у
21. Координати вектора
A x1 , y1 , z1e3
B x 2 , y 2 , z 2
О
e1
e2
AB x2 x1 , y2 y1 , z2 z1
22.
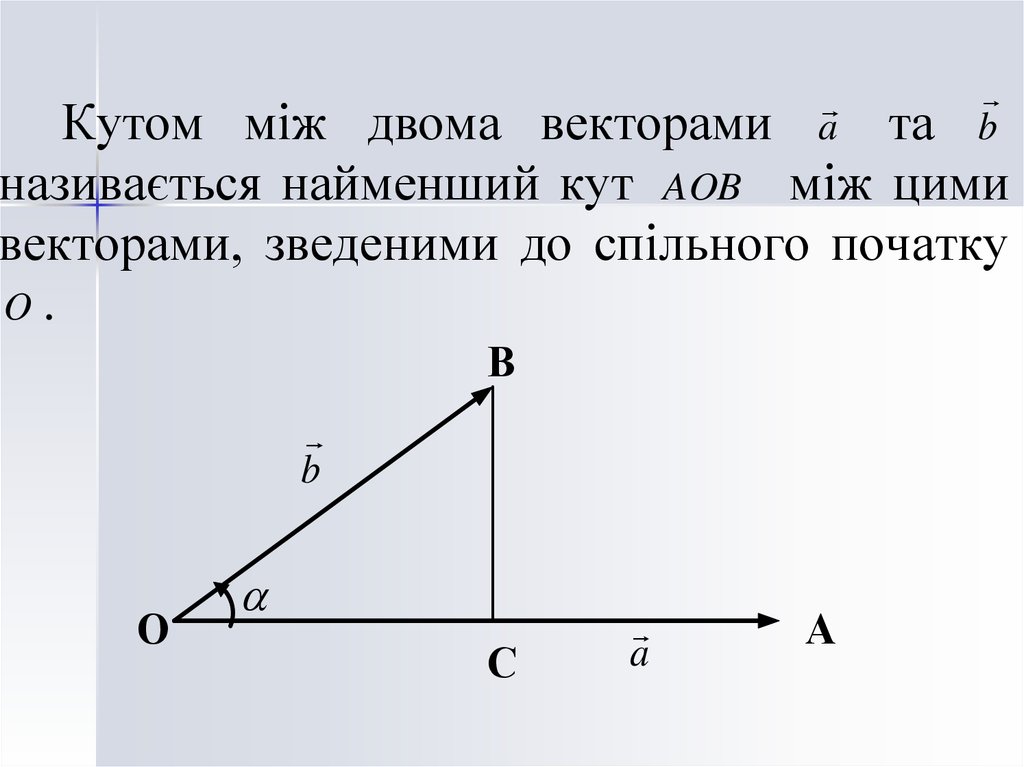
ab
Кутом між двома векторами
та
називається найменший кут AOB між цими
векторами, зведеними до спільного початку
O.
В
b
О
С
a
А
23.
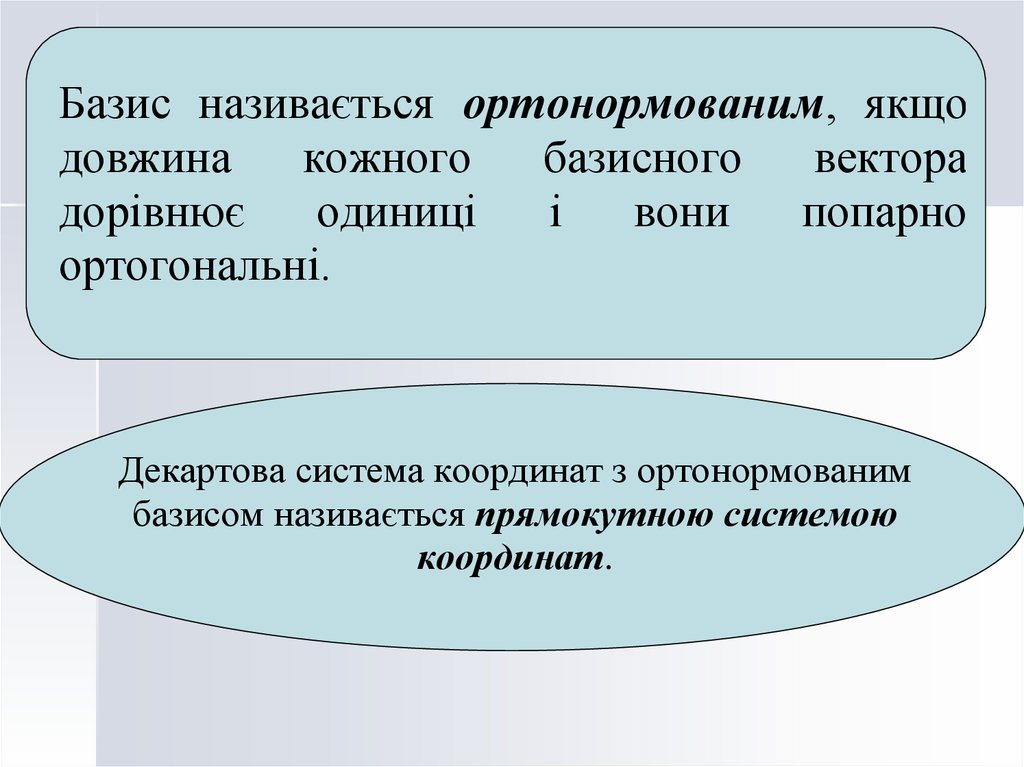
Базис називається ортонормованим, якщодовжина
кожного
базисного
вектора
дорівнює
одиниці
і
вони
попарно
ортогональні.
Декартова система координат з ортонормованим
базисом називається прямокутною системою
координат.
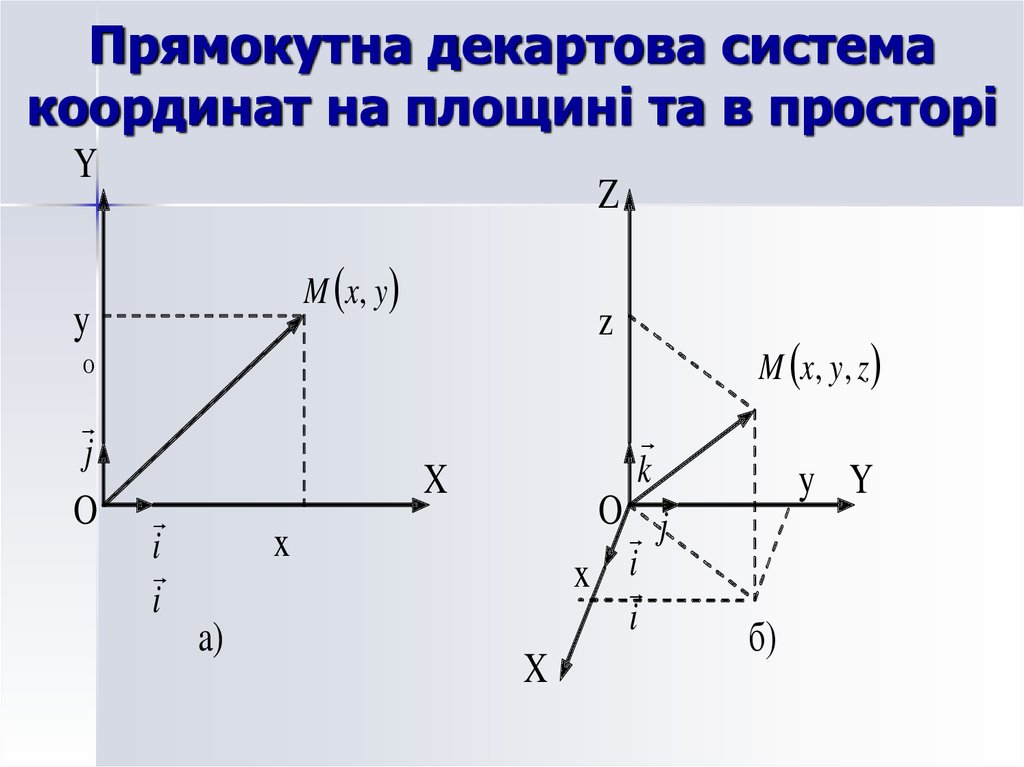
24. Прямокутна декартова система координат на площині та в просторі
YZ
M x, y
y
z
M x, y , z
O
j
O
k
X
i
i
O j
x i
i
x
a)
X
y Y
б)
25. Відстань між двома точками
На площиніd ( х 2 x 1 ) ( y 2 y1 ) .
2
2
В просторі
d ( x2 x1 ) ( y 2 y1 ) ( z 2 z1 ) .
2
2
2
26.
a ax , a y , az , b bx , by , bz2
2
2
a ax a y az
a b ax bx , a y by , az bz .
a a x , a y , az .
Напрямні косинуси
ay
az
ax
cos cos cos
|a|
|a|
|a|
27. Ділення відрізка в заданому відношенні
ТаМ1
Якщо M1 ( x1 , y1 , z1 ), M 2 ( x2 , y2 , z 2 ), M ( x, y, z)
M1M MM 2
М
М2
x1 x 2
y1 y 2
z1 z2
x
, y
, z
.
1
1
1
28. Означення
Скалярнимдобутком
двох
векторів
a і
b називається число, яке дорівнює
добутку модулів векторів a і b на
косинус кута між ними.
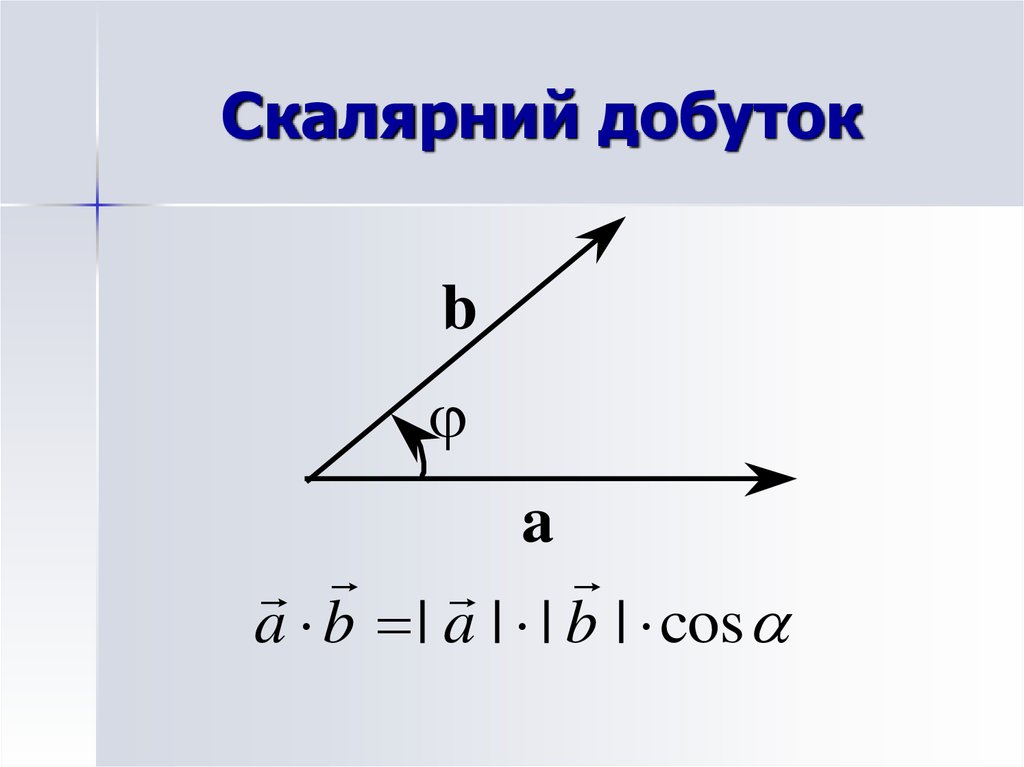
29. Скалярний добуток
ba
a b | a | | b | cos
30. властивості:
1.2.
Скалярний добуток
комутативний,
тобто
a b b a .
2
2
0
a a a | a | | a | cos 0 | a | ,
3. Скалярний добуток дорівнює нулю тоді і
тільки тоді, коли співмножники ортогональні
або хоча б один з них дорівнює нулю.
31.
4. Скалярний добуток асоціативний відносно скалярногомножника, тобто
( a )b a ( b ) (a b ) .
5. Скалярний добуток дистрибутивний відносно
додавання, тобто для довільних трьох векторів a , b с
має місце рівність
a (b c ) a b a c .
6. Вектори ортонормованого базису задовольняють
співвідношення
i i j j k k 1,
i j i k j k 0 .
32. Вираз скалярного добутку через координати
Якщо a {a x , a y , a z } b {bx , b y , bz } ,тоді
a b a x bx a y b y a z bz
33. Застосування: 1. Кут між векторами
a bcos
| a | |b |
cos
a x bx a y b y a z bz
a x a y a z bx b y bz
2
2
2
2
2
2
34. 2. Умова ортогональності двох векторів
a x bx a y b y a z bz 035. 3. Фізичний зміст
якщо матеріальна точка, на яку дієсила, здійснила переміщення s ,
То робота дорівнює скалярному
добутку сили на переміщення
A F, s
36.
Векторним добутком вектора a на вектор bназивається вектор с , в якого:
1) довжина чисельно дорівнює площі
паралелограма, побудованго на цих векторах;
2) вектор с перпендикулярний
до площини, в якій
лежать вектори
a і b , тобто
c a і c b ;
3) вектор с напрямлений таким чином, щоб
найкоротший поворот від вектора a до b
здійснювався проти годинникової стрілки, якщо
дивитись на нього з кінця вектора c .
37. Векторний добуток
c a bb
О
c1 b a
a
c | a b | a b sin
38. Властивості:
[a , b ] [b , a ] - антикомутативність;[ a , b ] [a , b ]; [a , b ] [a , b ]
асоціативність відносно скалярного множника;
[a b , c ] [a , c ] [b , c ]
дистрибутивність
відносно додавання;
[ a , b ] 0 означає колінеарність векторів
aіb
.
39. векторний добуток основних ортів
ij
k
i
0
k
j
j
k
0
i
k
j
i
0
40. Вираз векторного добутку через координати
Якщо a {a x , a y , a z } b x , y , z , ,2
2
2
тоді
i
a b x1
j
y1
k
z1
x2
y2
z2
41. Застосування: 1. умова колінеарності векторів
x1y1 z1
x2 y 2 z 2
42. 2. Геометричний зміст
Площа паралелограмаS а b
Площа трикутника
1
S a b
2
43. 3. Фізичний зміст
Момент силиM r F
44. Мішаний добуток трьох векторів
Мішаним добутком трьох векторівa, b
і
c
називається
число, яке отримуємо, якщо перемножимо вектори
a
і
b
векторно, а потім отриманий вектор помножимо скалярно
на вектор
c.
a , b , c ([ a , b ], c )
45. Геометричний зміст
Мішаний добутокнекомпланарних
векторів a , b і c по модулю дорівнює
об’єму паралелепіпеда,
побудованого
на
векторах a, b , c .
46.
a, bc
Вектори
і задані своїми координатами в
прямокутній системі координат
a x1 , y1 , z1 ; b x 2 , y 2 , z 2 , c x3 , y 3 , z 3
x1
a, b , c x2
x3
y1
z1
y2
y3
z2
z3
47. Умова компланарності
x1y1
z1
x2
x3
y2
y3
z2 0
z3
48. Властивості:
([ a , b ], c ) (a , [b , c ])a, b , c b , c , a c , a, b
a, b , c b , a, c
49. Подвійний векторний добуток
Подвійним векторним добуткомвекторів a , b , c називається вираз виду
[ a,[b, c]] .
[a,[b, c]] b(a, c) c(a, b)
50. Завдання на самопідготовку
Законспектувати і вивчити слайди:5-10, 19-27, 30-31, 33-35.
Шумко Л.І. , Шумко Л.Г. Вища
математика, курс лекцій, 2005.
§2.1-2.5.

















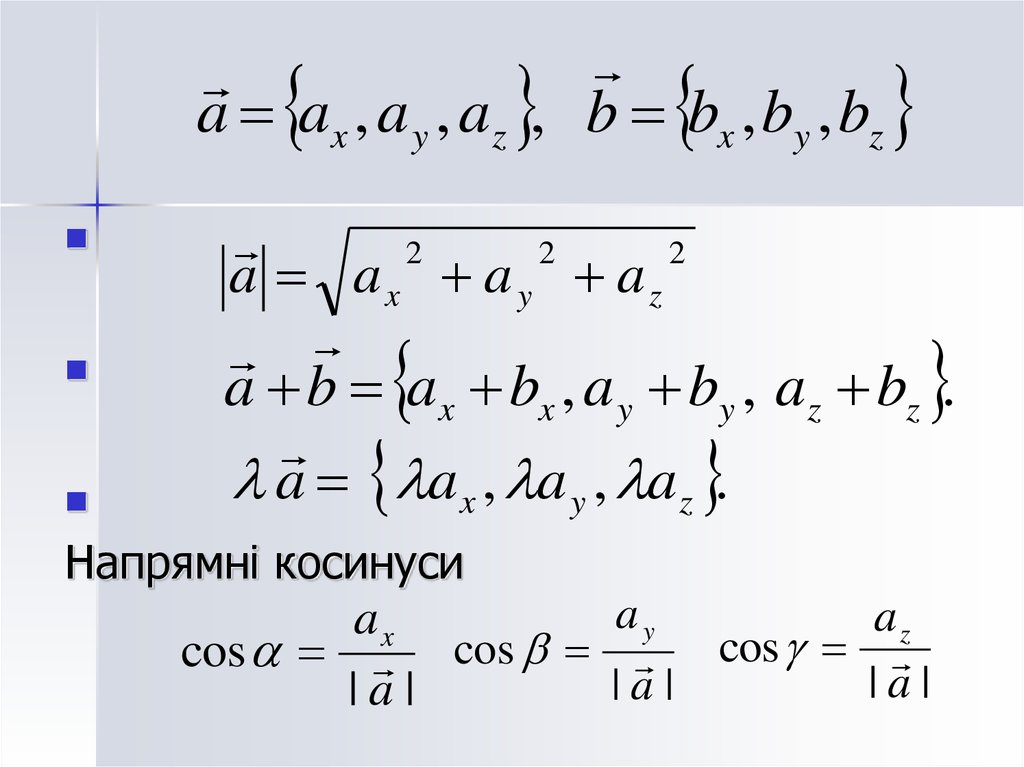




















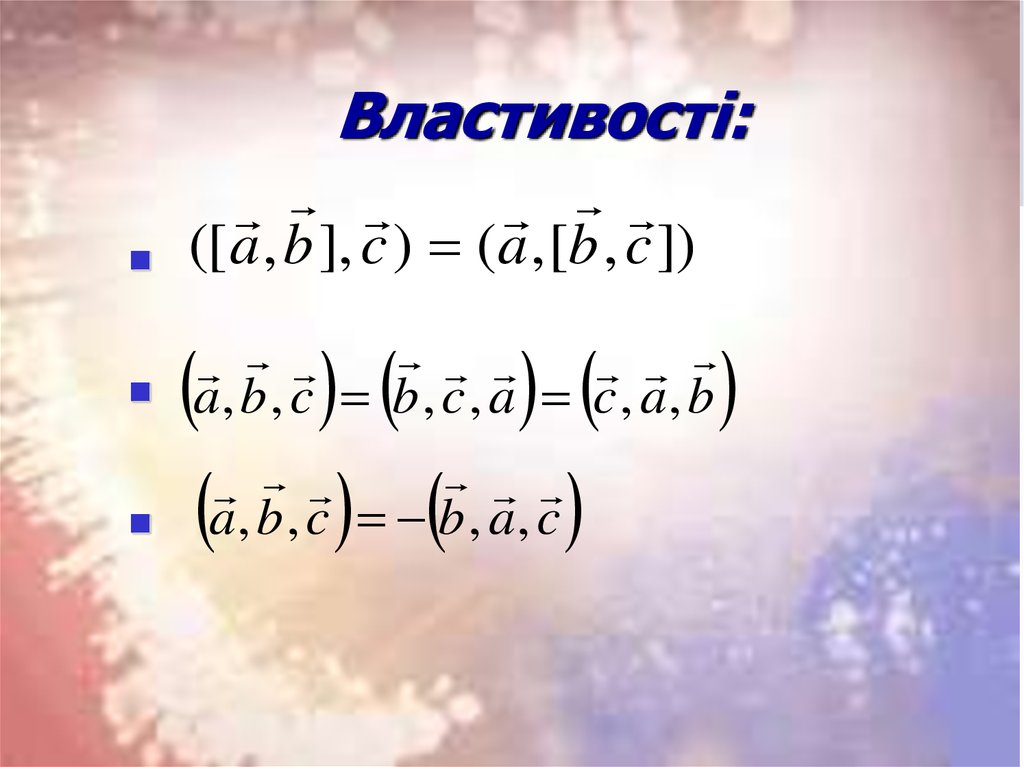


 Математика
Математика








