Электростатика (лекция 6)

1.

ВоГУ
Лекция 6
Электростатика
Кузина Л.А.,
к.ф.-м.н., доцент
2020 г.
1

2.

2

3.

• Электризация при трении
• 2 сорта зарядов: + и –
• Носители заряда – элементарные частицы
• Заряд частиц дискретен: q=±N.e
• Элементарный заряд e=1.6.10-19 Кл :
• Заряд не зависит от системы отсчёта
e e 2
X e e X
• Закон сохранения заряда:
• В электрически изолированной системе
Σq=const

4.

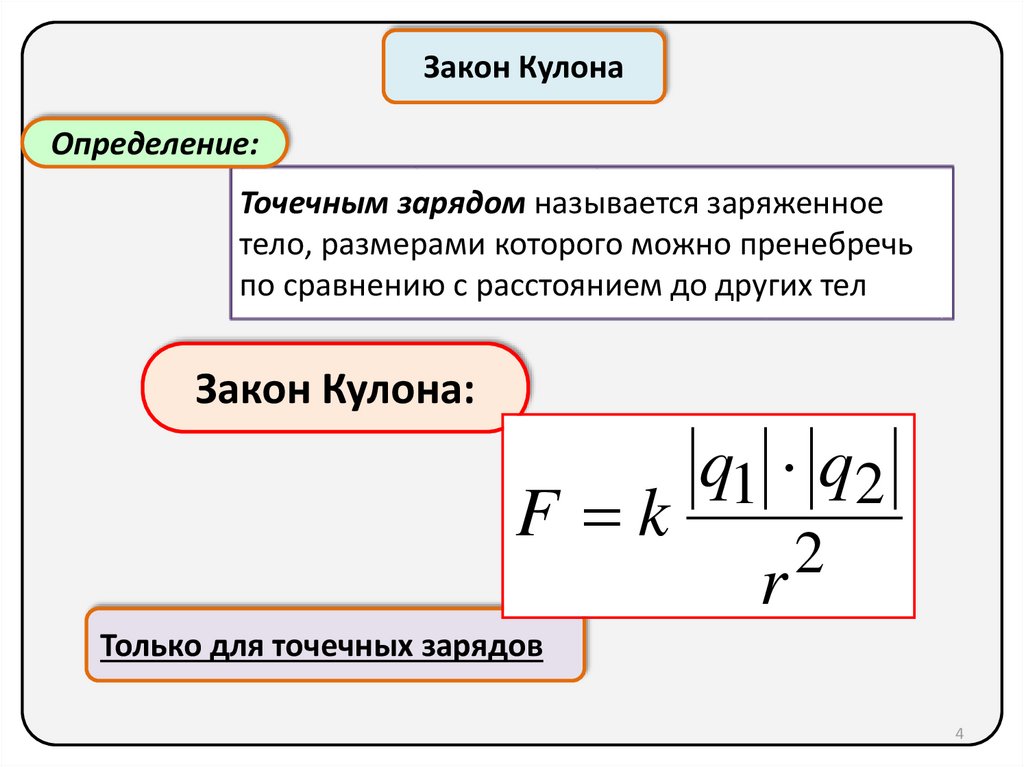
Закон Кулона
Определение:
Точечным зарядом называется заряженное
тело, размерами которого можно пренебречь
по сравнению с расстоянием до других тел
Закон Кулона:
q1 q2
F k
2
r
Только для точечных зарядов
4

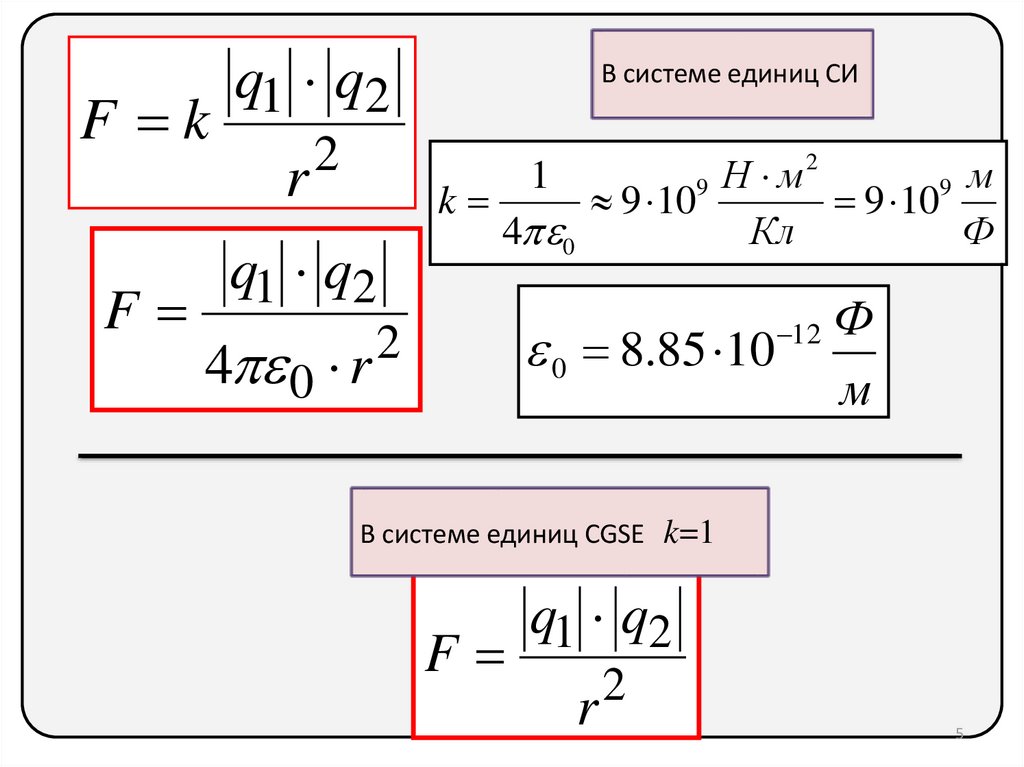
5.

q1 q2
F k
2
r
F
q1 q2
4 0 r
В системе единиц СИ
2
Н
м
9
9 м
k
9 10
9 10
4 0
Кл
Ф
1
0 8.85 10
2
12
Ф
м
В системе единиц CGSE k=1
F
q1 q2
r
2
5

6.

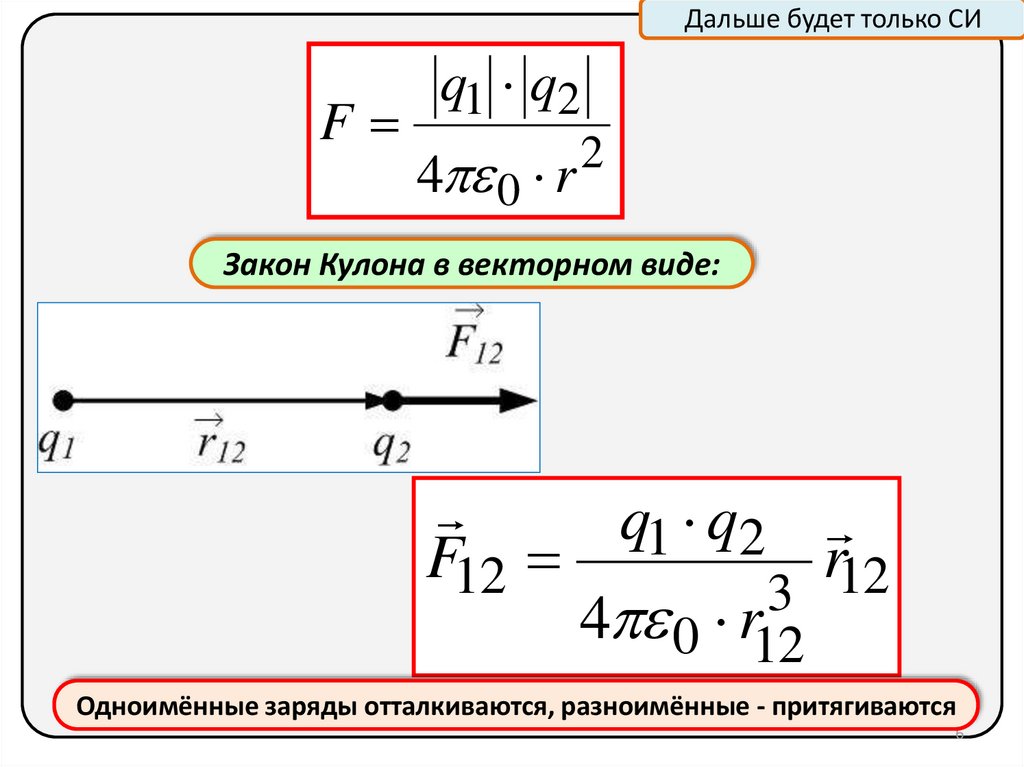
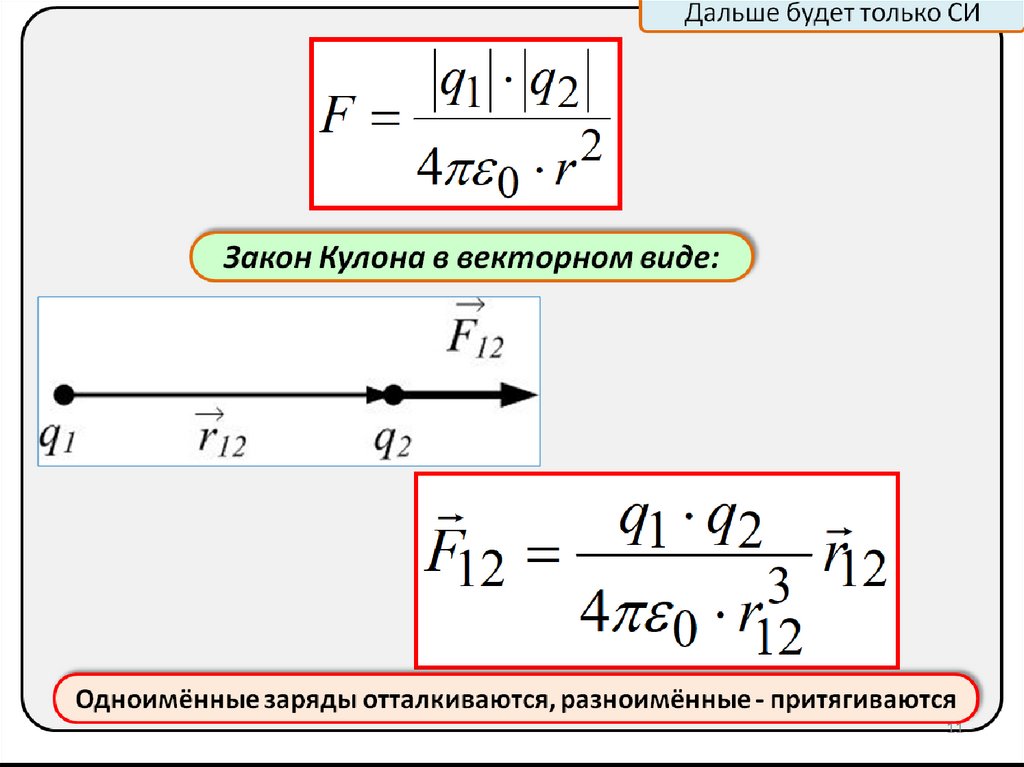
Дальше будет только СИ
F
q1 q2
4 0 r
2
Закон Кулона в векторном виде:
q1 q2
F12
r12
3
4 0 r12
Одноимённые заряды отталкиваются, разноимённые - притягиваются
6

7.

8.

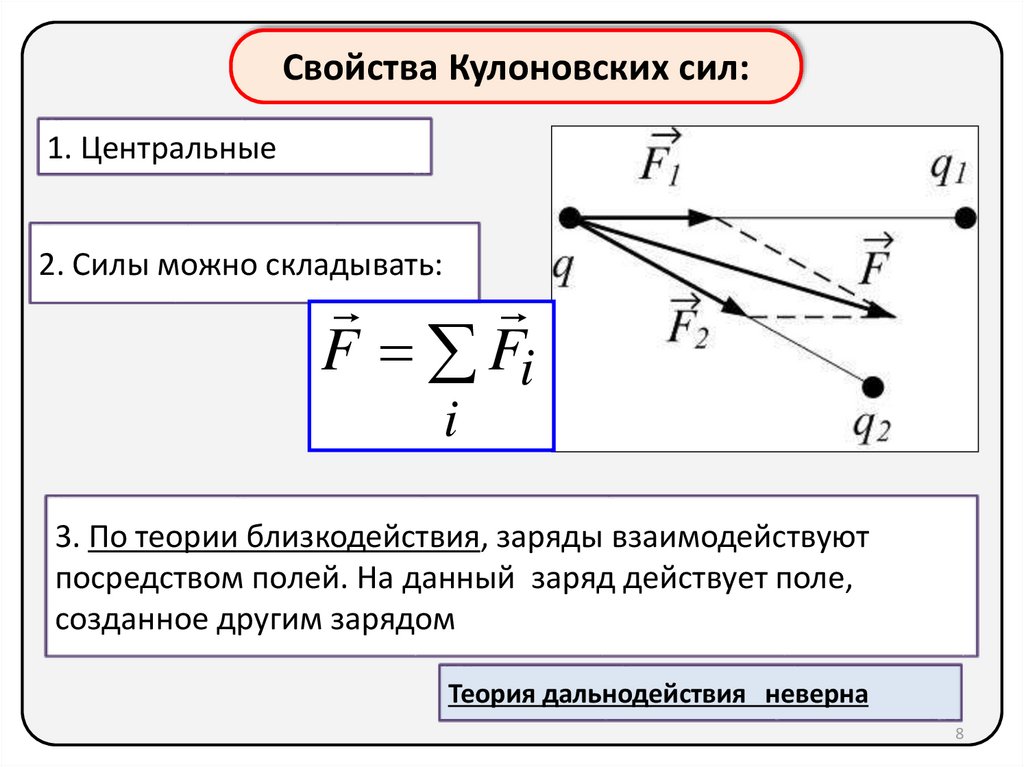
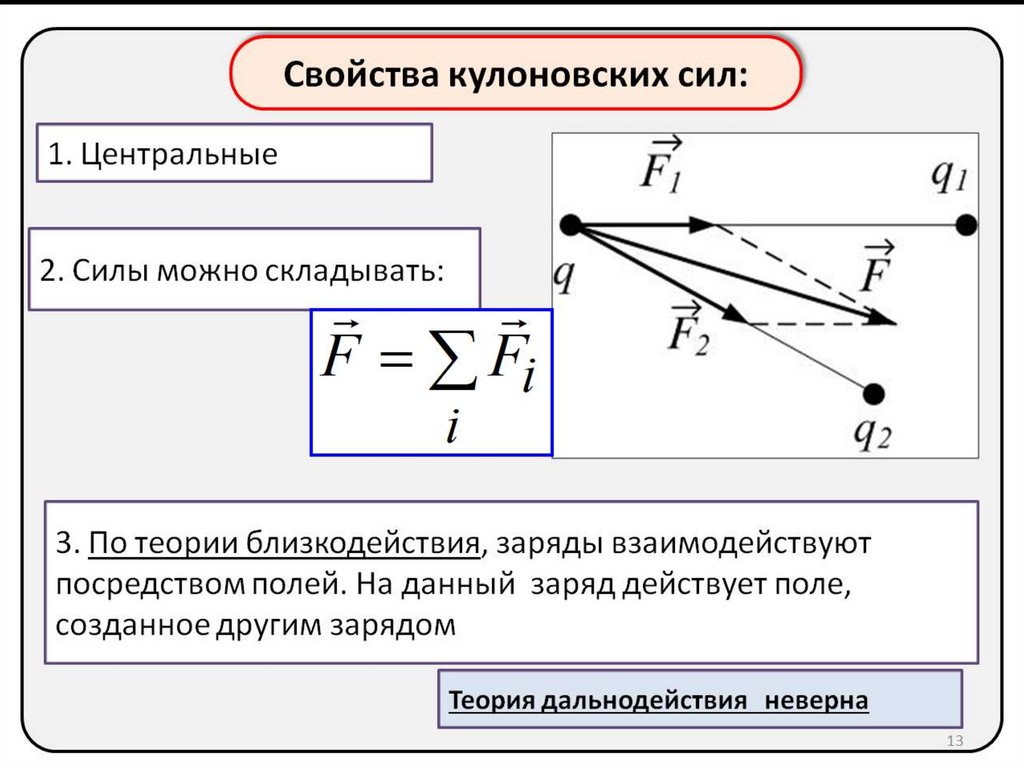
Свойства Кулоновских сил:
1. Центральные
2. Силы можно складывать:
F Fi
i
3. По теории близкодействия, заряды взаимодействуют
посредством полей. На данный заряд действует поле,
созданное другим зарядом
Теория дальнодействия неверна
8

9.

10.

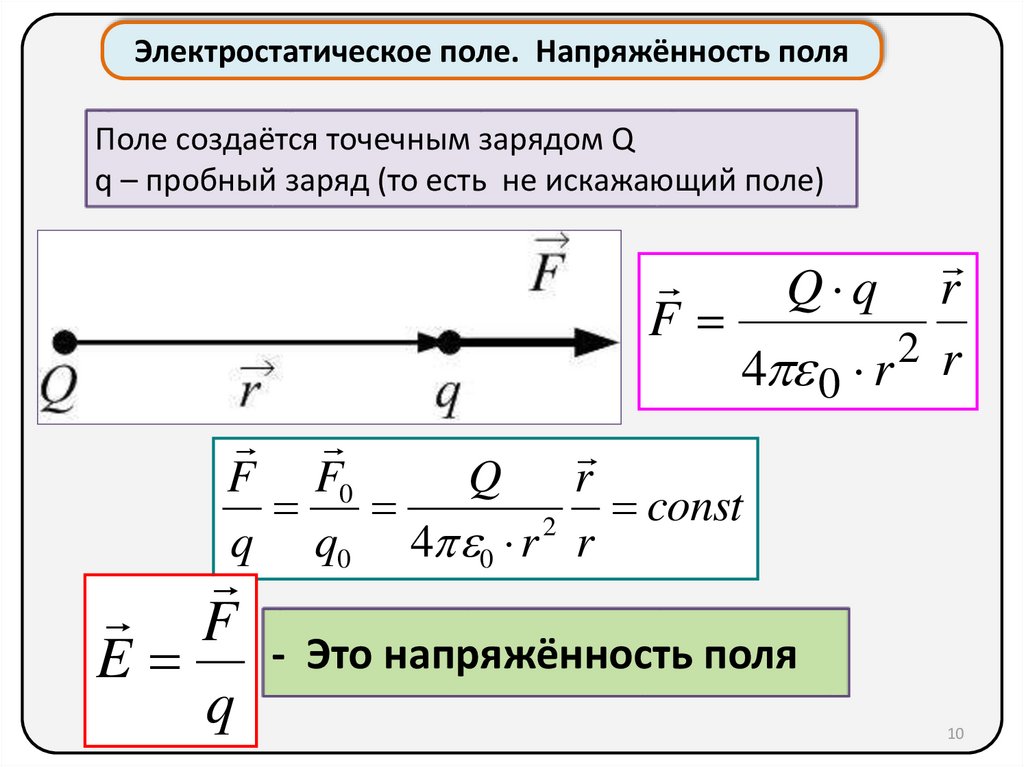
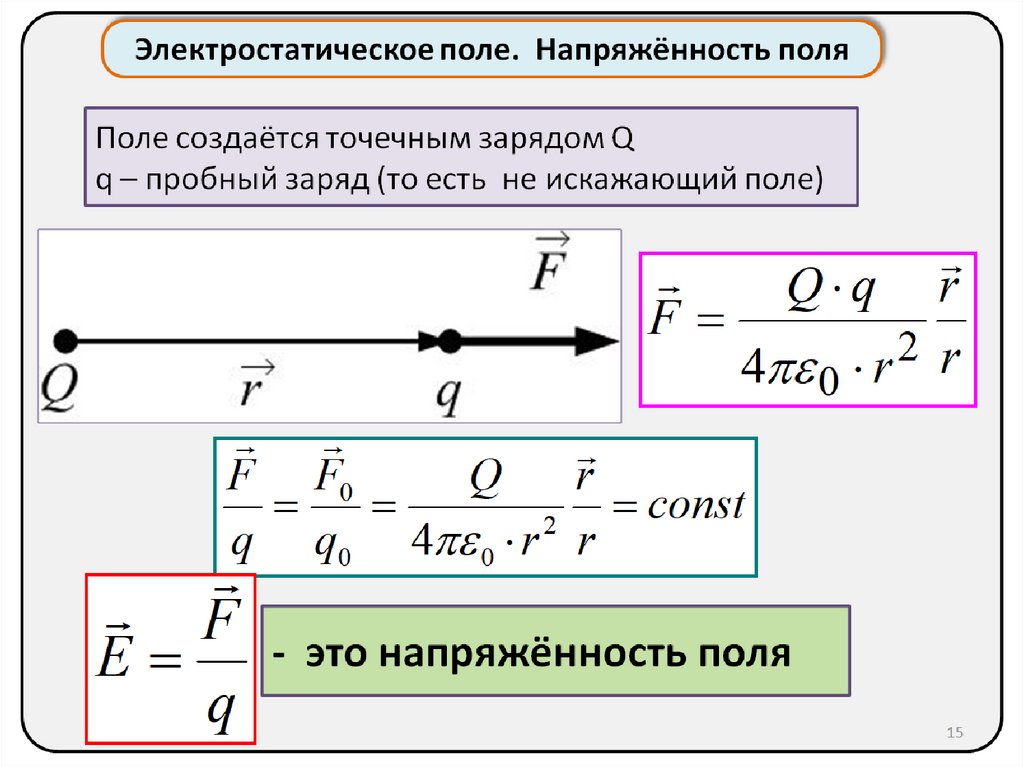
Электростатическое поле. Напряжённость поля
Поле создаётся точечным зарядом Q
q – пробный заряд (то есть не искажающий поле)
Q q r
F
2 r
4 0 r
F F0
Q
r
const
2
q q0 4 0 r r
F
E
q
- Это напряжённость поля
10

11.

12.

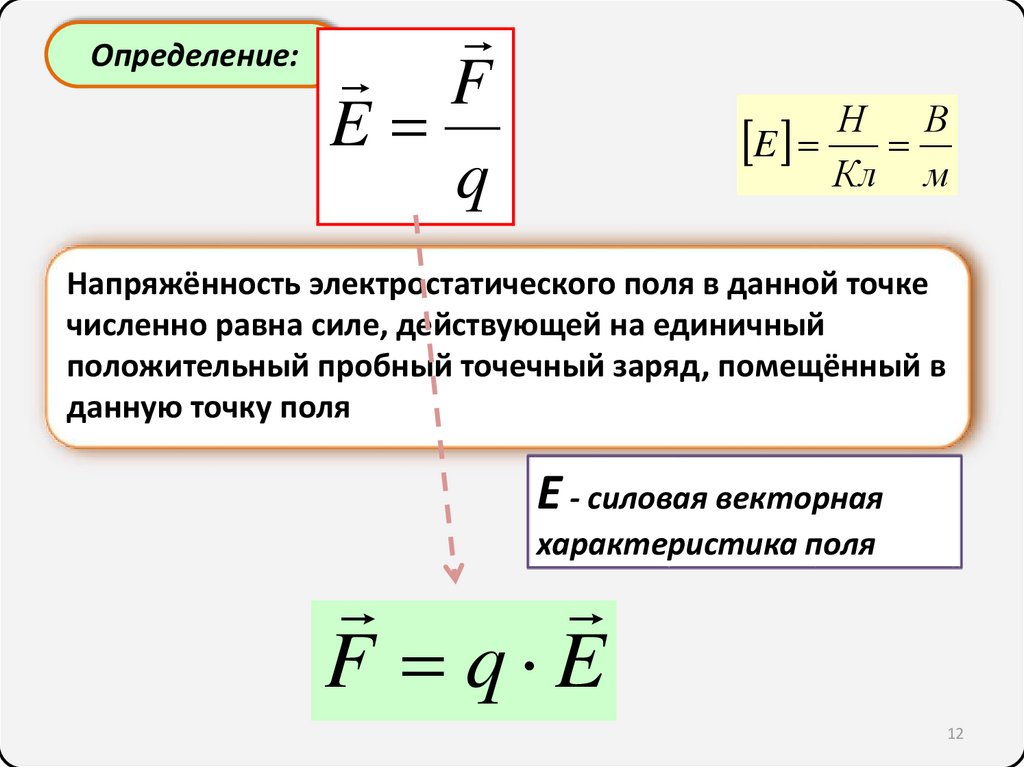
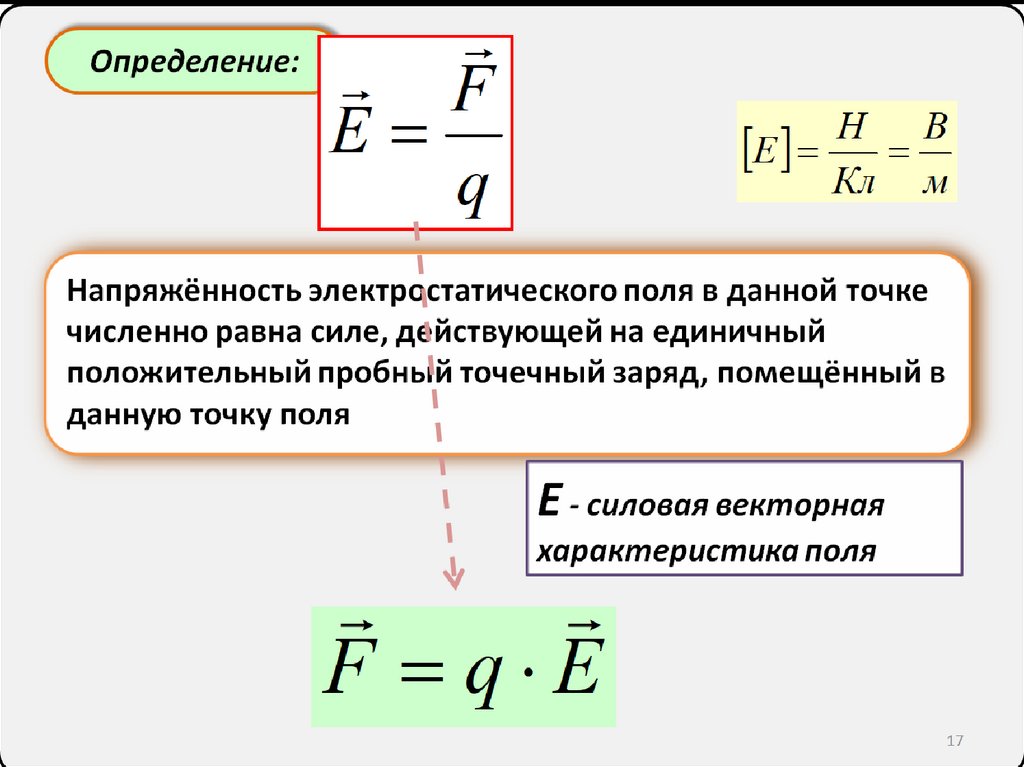
Определение:
F
E
q
Н
В
E
Кл м
Напряжённость электростатического поля в данной точке
численно равна силе, действующей на единичный
положительный пробный точечный заряд, помещённый в
данную точку поля
Е - силовая векторная
характеристика поля
F q E
12

13.

14.

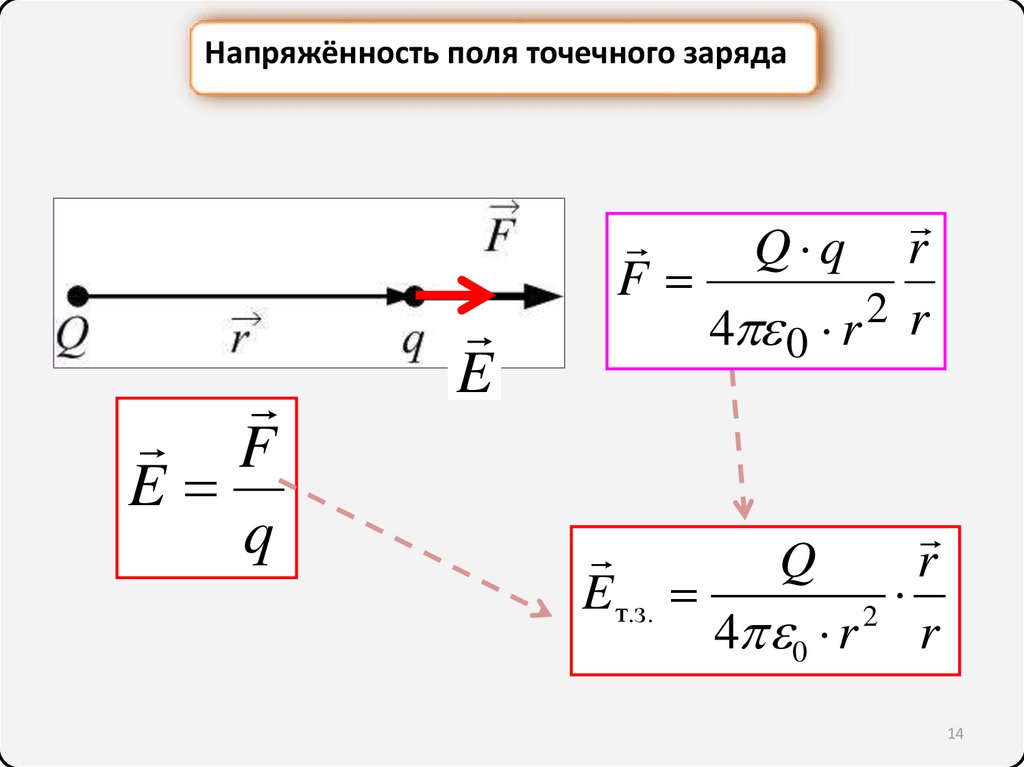
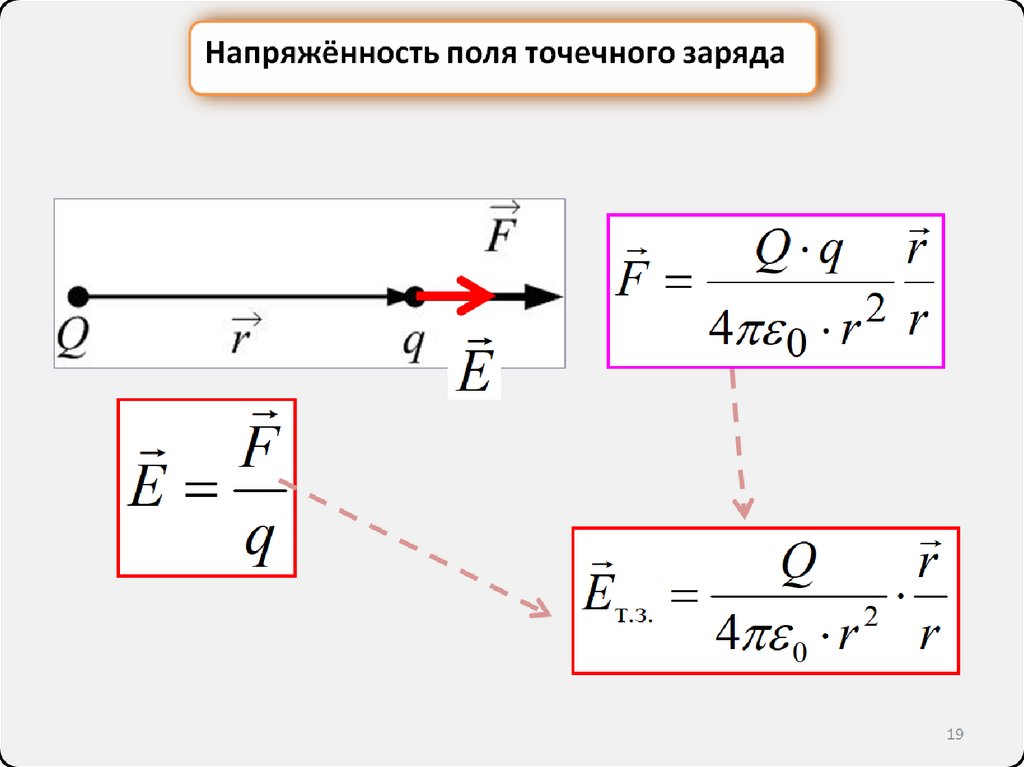
Напряжённость поля точечного заряда
F
E
q
E
Q q r
F
2 r
4 0 r
Eт.з.
Q
r
2
4 0 r r
14

15.

16.

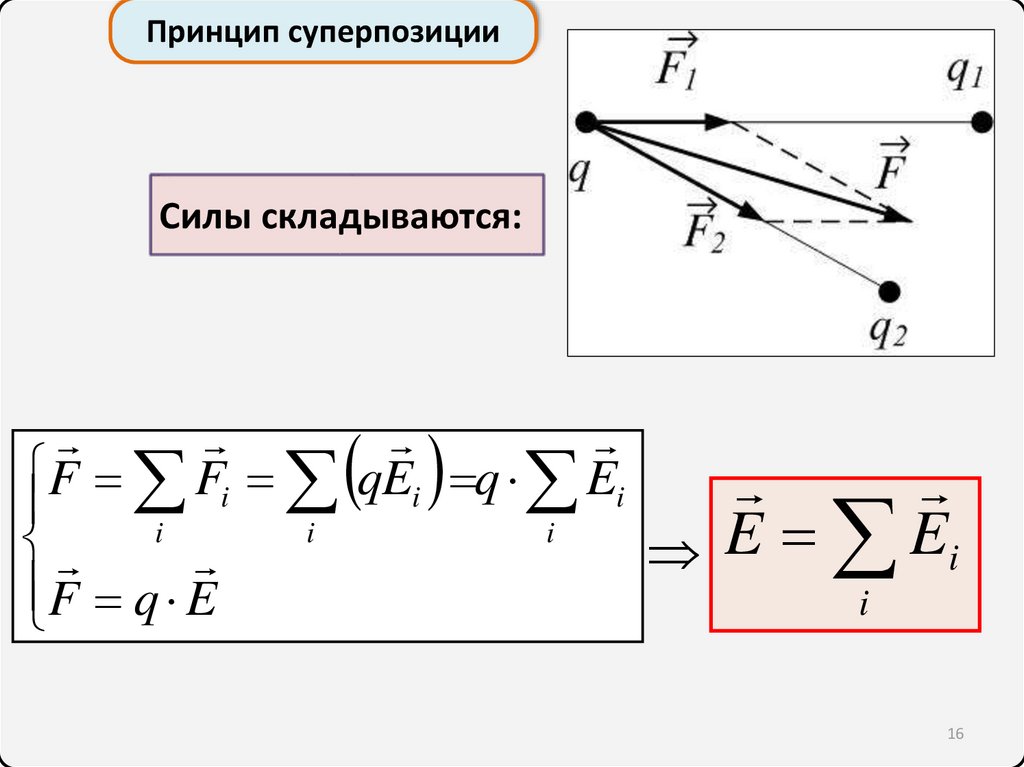
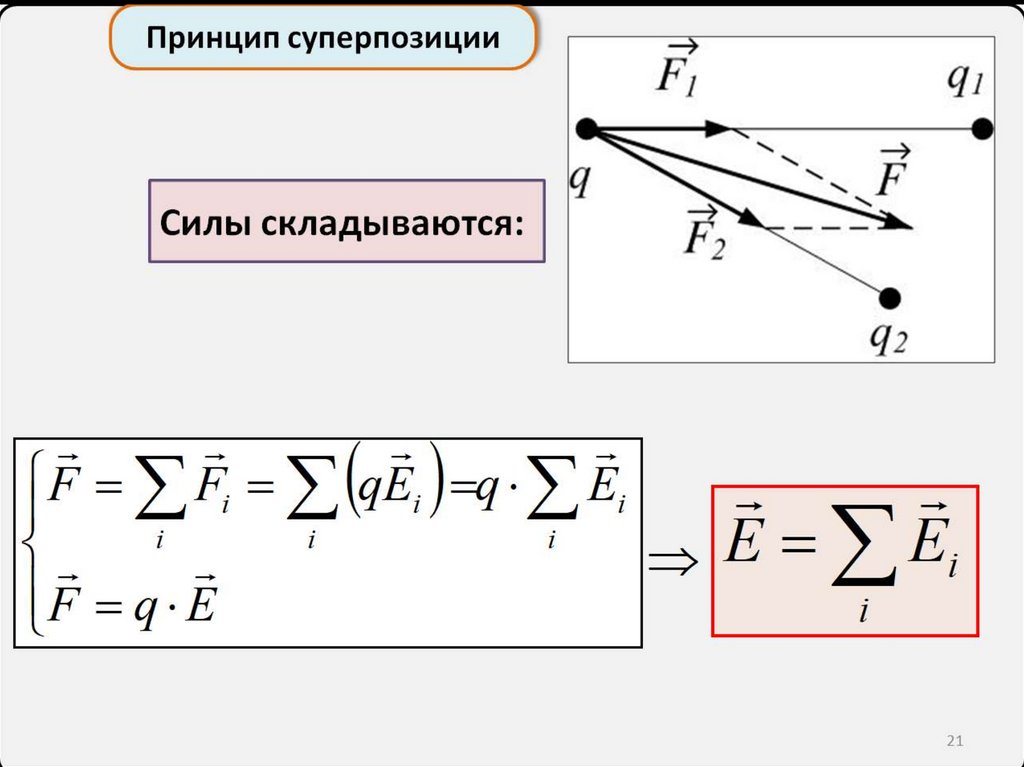
Принцип суперпозиции
Силы складываются:
F Fi qEi q Ei
i
i
i
F q E
E Ei
i
16

17.

18.

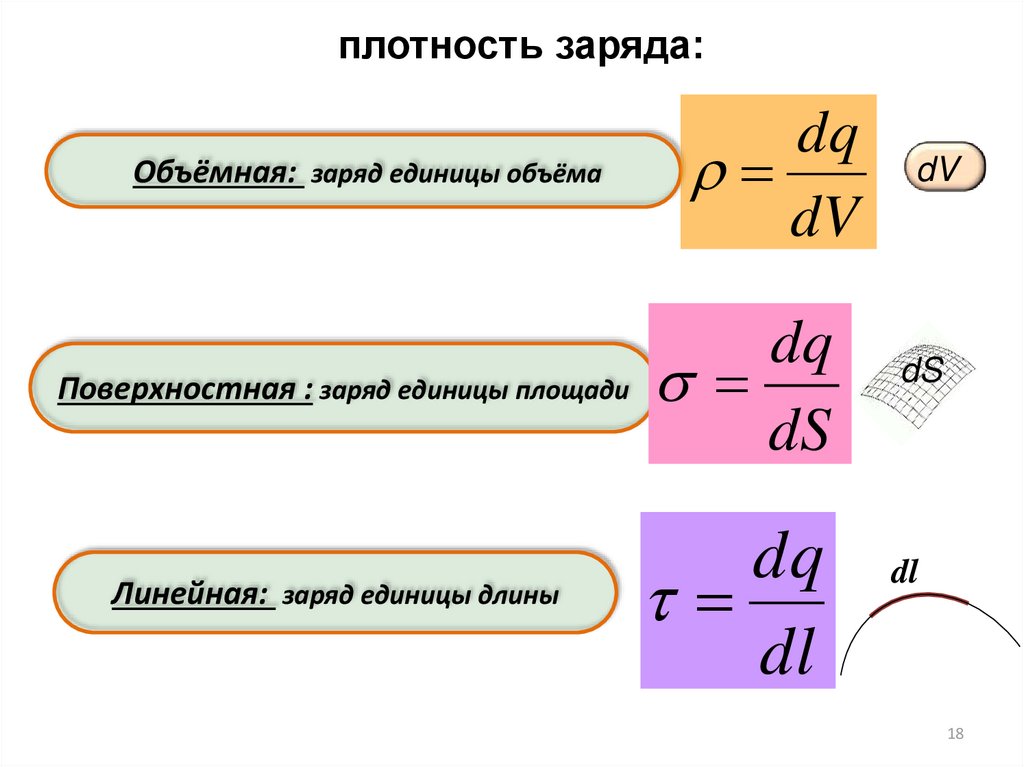
плотность заряда:
Объёмная: заряд единицы объёма
dq
dV
Поверхностная : заряд единицы площади
dq
dS
Линейная: заряд единицы длины
dq
dl
dV
dS
dl
18

19.

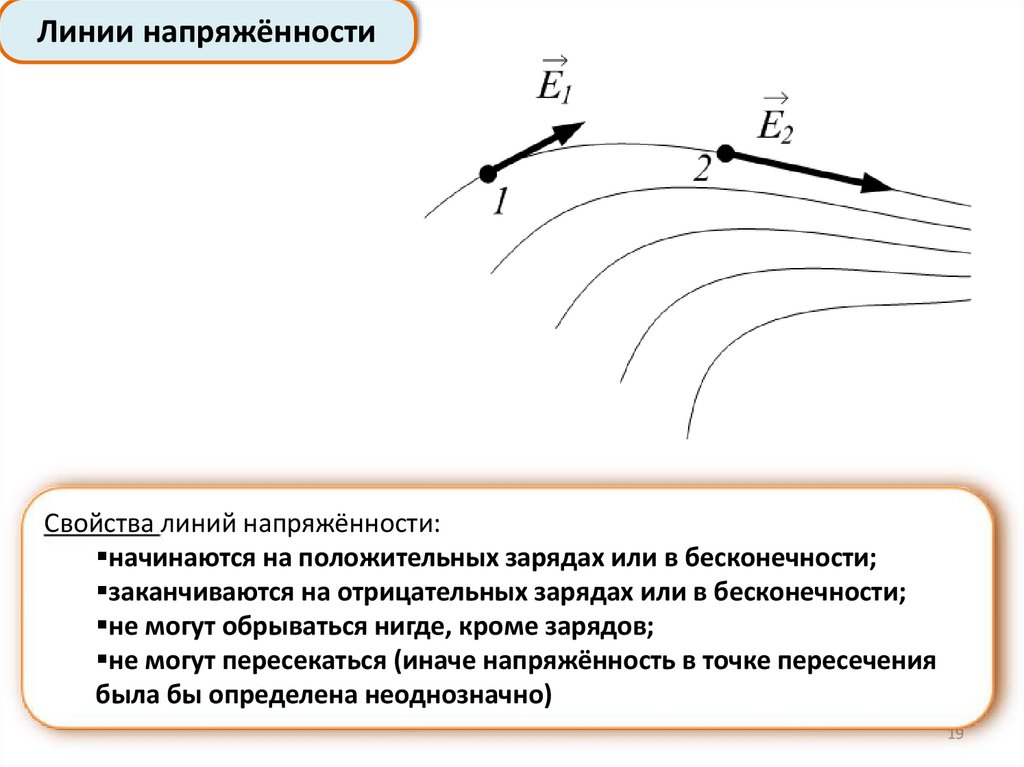
Линии напряжённости
Cвойства линий напряжённости:
начинаются на положительных зарядах или в бесконечности;
заканчиваются на отрицательных зарядах или в бесконечности;
не могут обрываться нигде, кроме зарядов;
не могут пересекаться (иначе напряжённость в точке пересечения
была бы определена неоднозначно)
19

20.

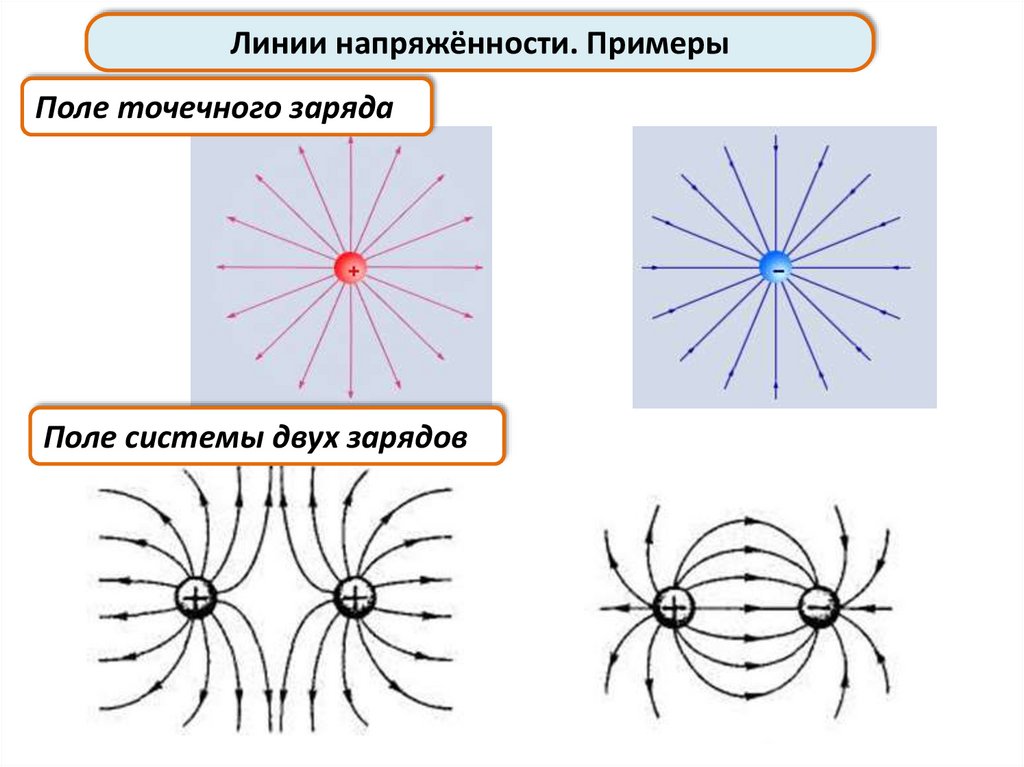
Линии напряжённости. Примеры
Поле точечного заряда
Поле системы двух зарядов

21.

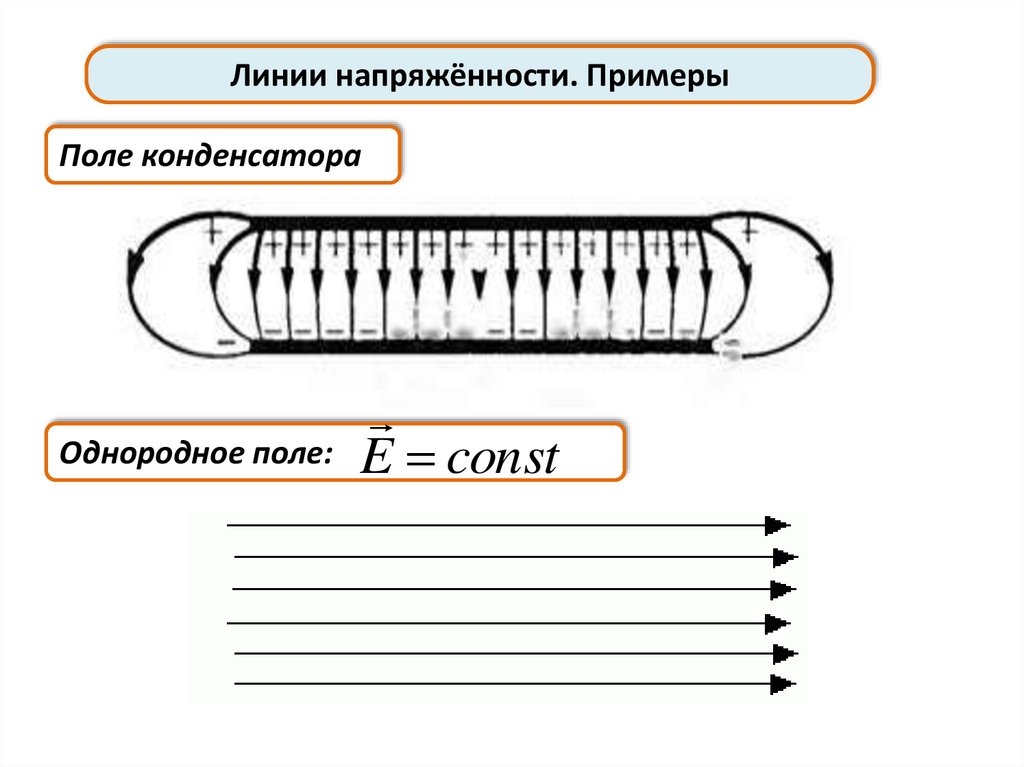
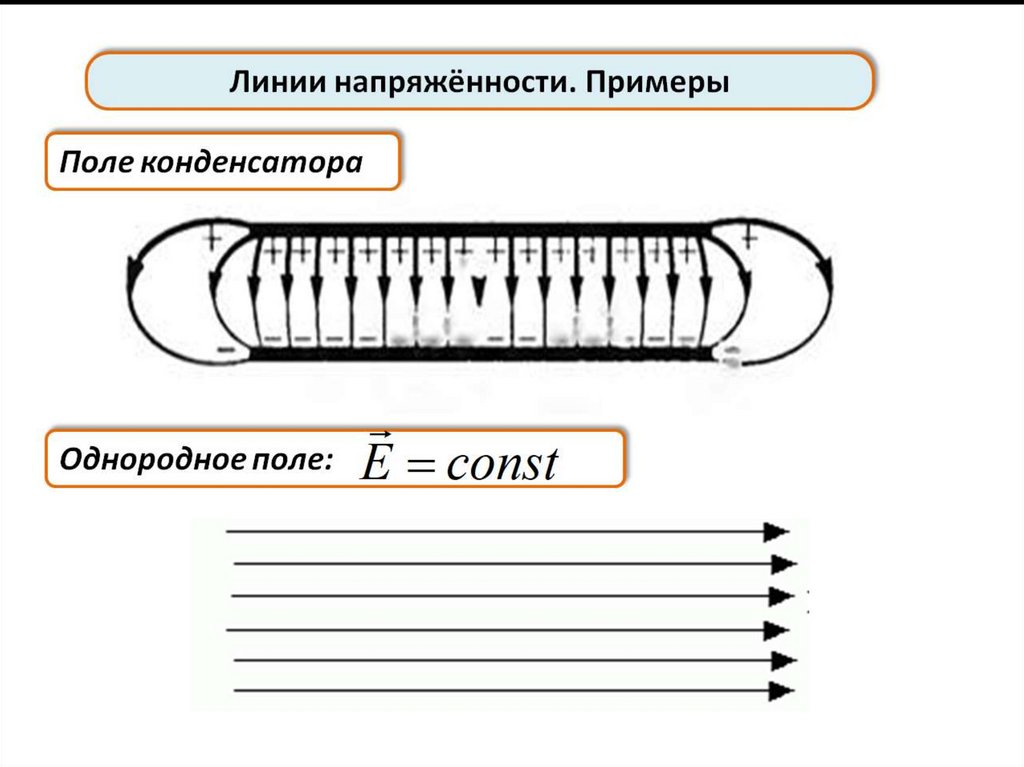
Линии напряжённости. Примеры
Поле конденсатора
Однородное поле:
E const

22.

23.

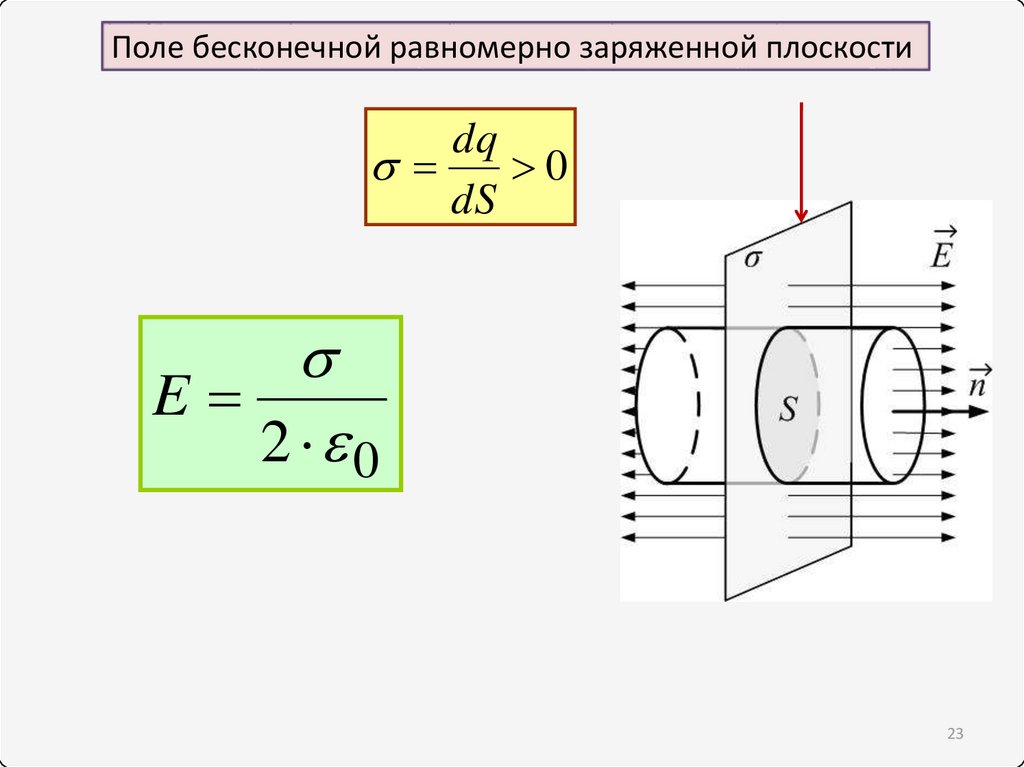
Поле бесконечной равномерно заряженной плоскости
dq
0
dS
E
2 0
23

24.

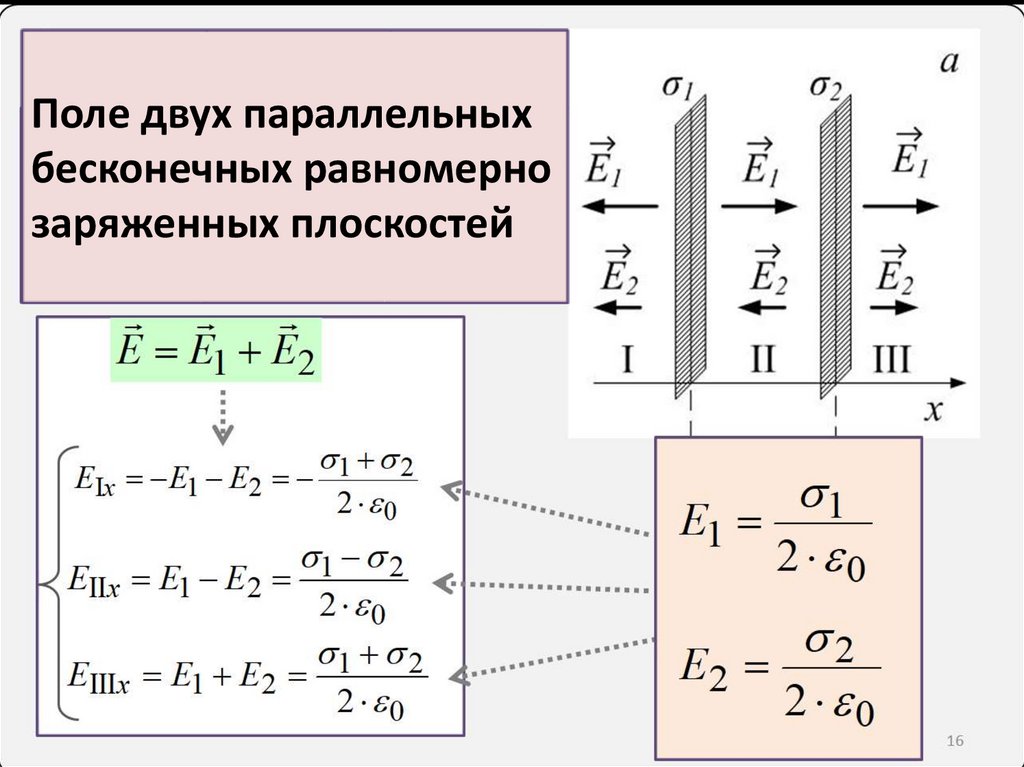
Поле двух параллельных
бесконечных равномерно
заряженных плоскостей

25.

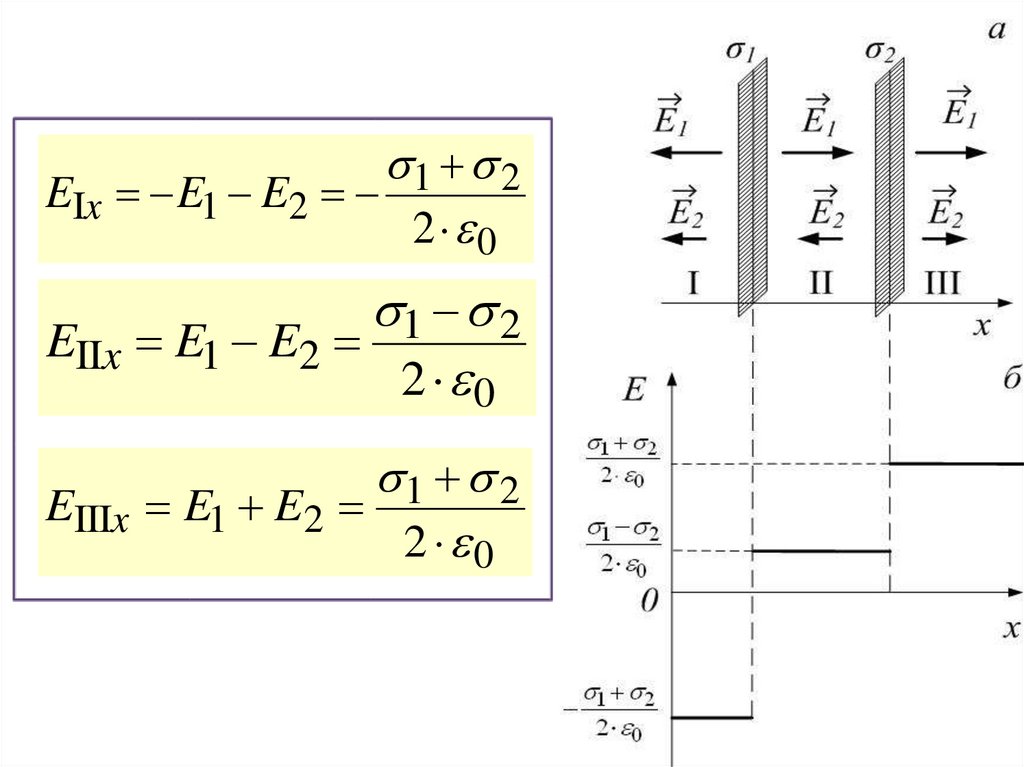
1 2
EIx E1 E2
2 0
1 2
EIIx E1 E2
2 0
1 2
EIIIx E1 E2
2 0
25

26.

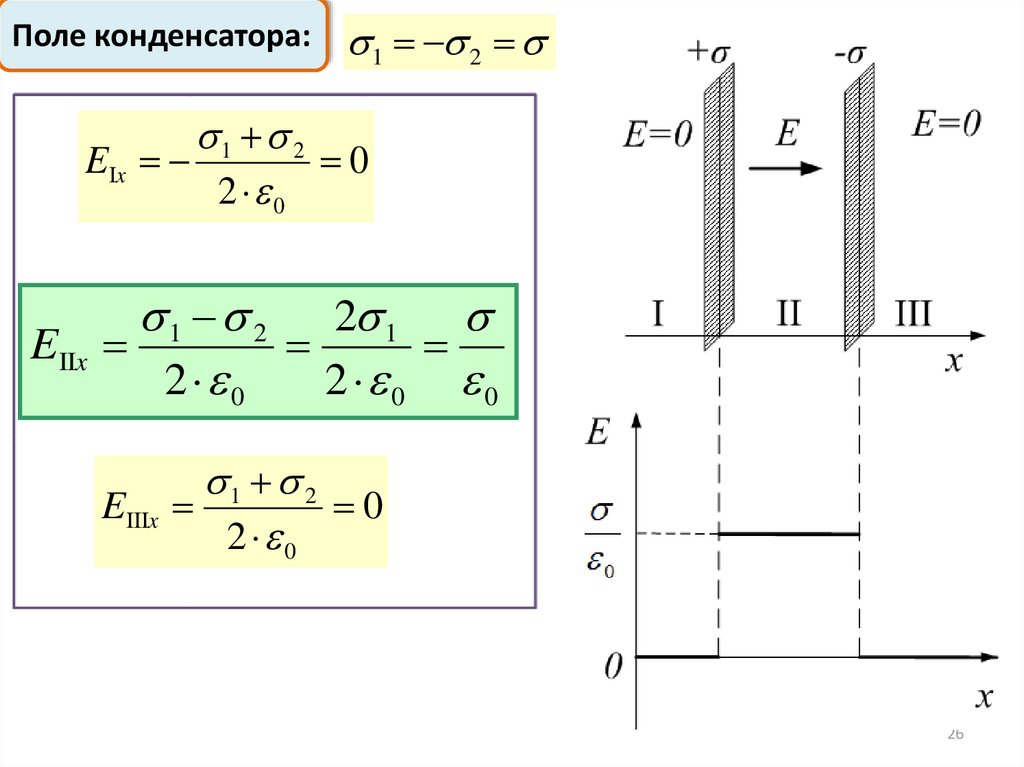
Поле конденсатора:
1 2
1 2
EIx
0
2 0
1 2 2 1
EIIx
2 0
2 0 0
EIIIx
1 2
0
2 0
26

27.

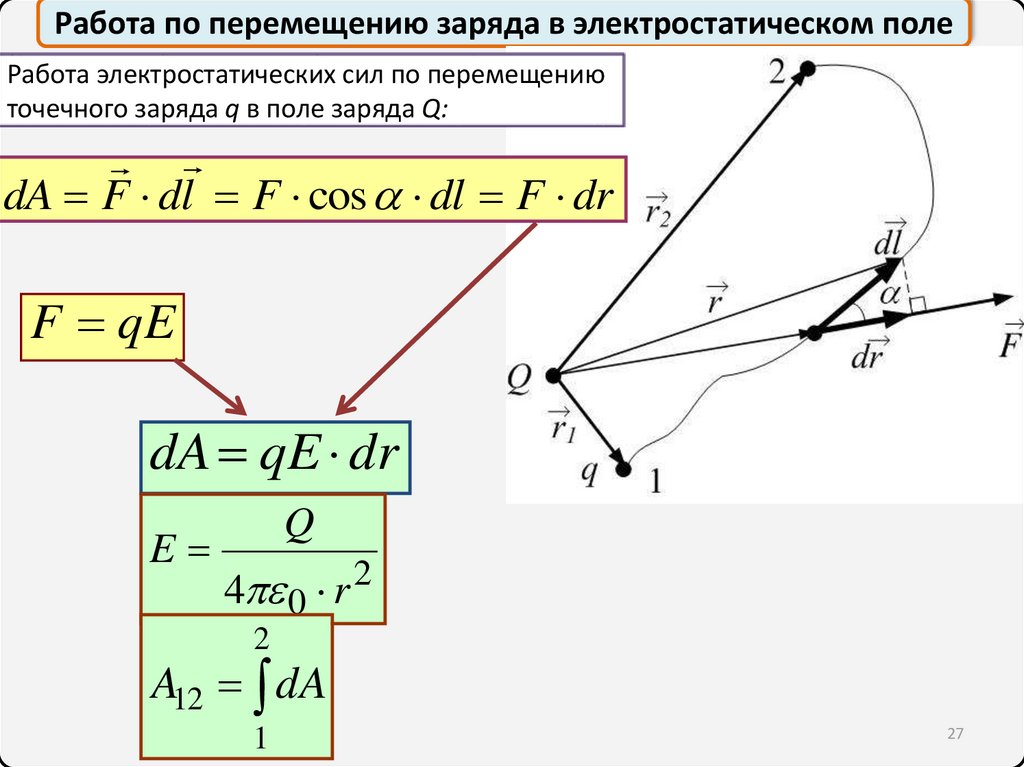
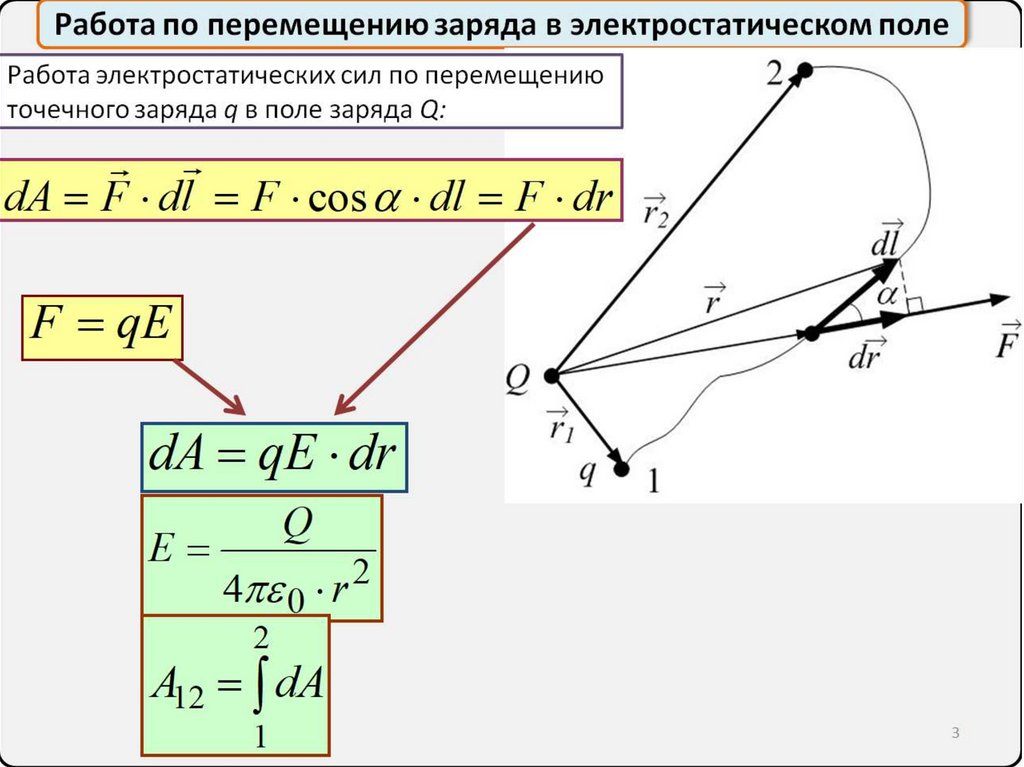
Работа по перемещению заряда в электростатическом поле
Работа электростатических сил по перемещению
точечного заряда q в поле заряда Q:
dA F dl F cos dl F dr
F qE
dA qE dr
E
Q
4 0 r 2
2
A12 dA
1
27

28.

29.

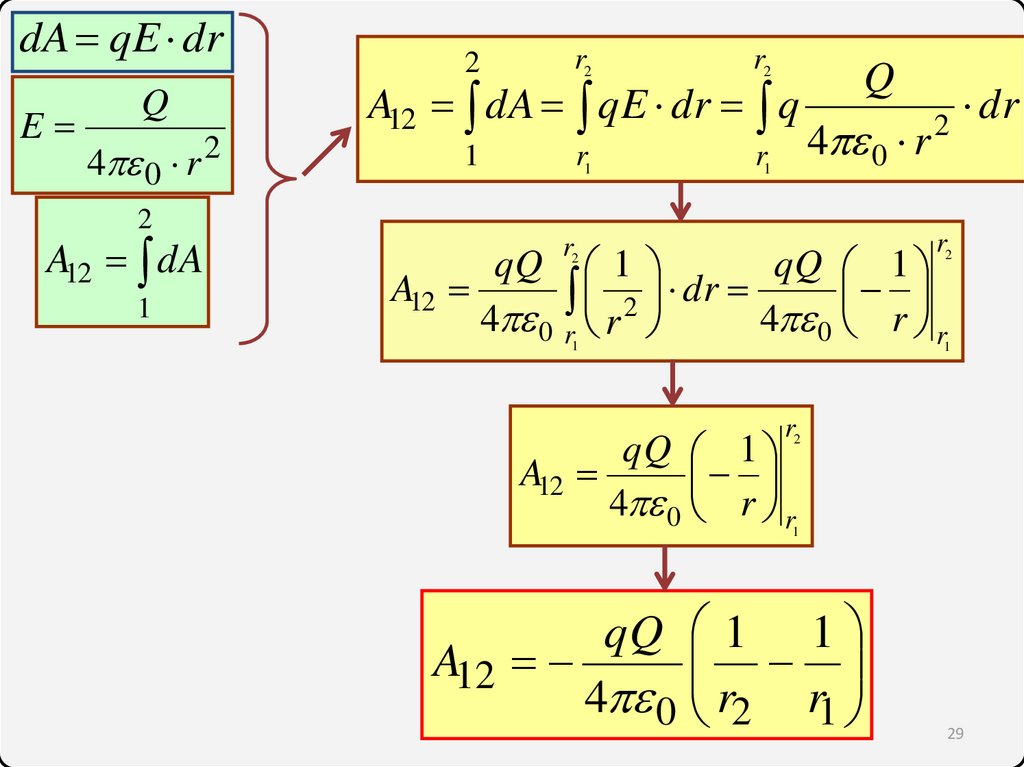
dA qE dr
E
Q
4 0 r 2
2
r2
r2
1
r1
r1
A12 dA qE dr q
Q
4 0 r
2
A12 dA
1
dr
2
r2
r2
1
1
qQ 1
qQ 1
A12
2 dr
4 0 r r
4 0 r r
r2
qQ 1
A12
4 0 r r
1
qQ 1 1
A12
4 0 r2 r1
29

30.

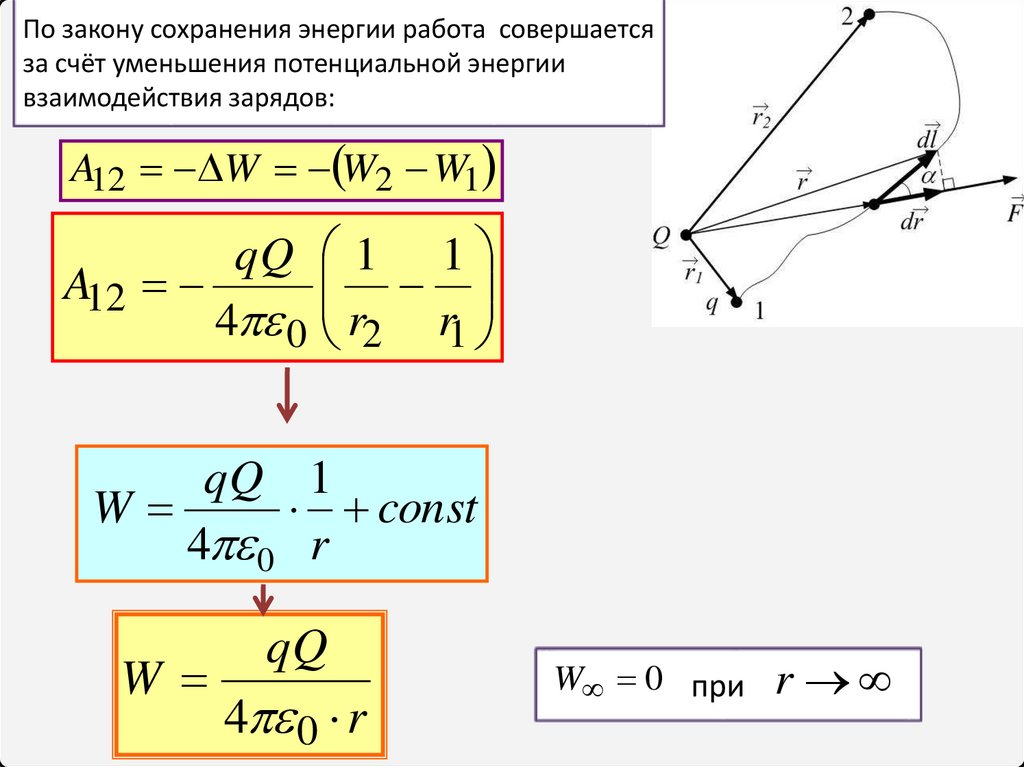
По закону сохранения энергии работа совершается
за счёт уменьшения потенциальной энергии
взаимодействия зарядов:
A12 W W2 W1
qQ 1 1
A12
4 0 r2 r1
qQ 1
W
const
4 0 r
qQ
W
4 0 r
W 0 при
r

31.

Потенциальный характер электростатического поля
qQ 1 1
A12
4 0 r2 r1
Работа не зависит от траектории, а только от начального и
конечного положения заряда q.
Электростатическое поле потенциально
Потенциальны поля только неподвижных зарядов
Для замкнутой траектории: r1 r2
qQ 1 1
0
A
4 0 r2 r1
31

32.

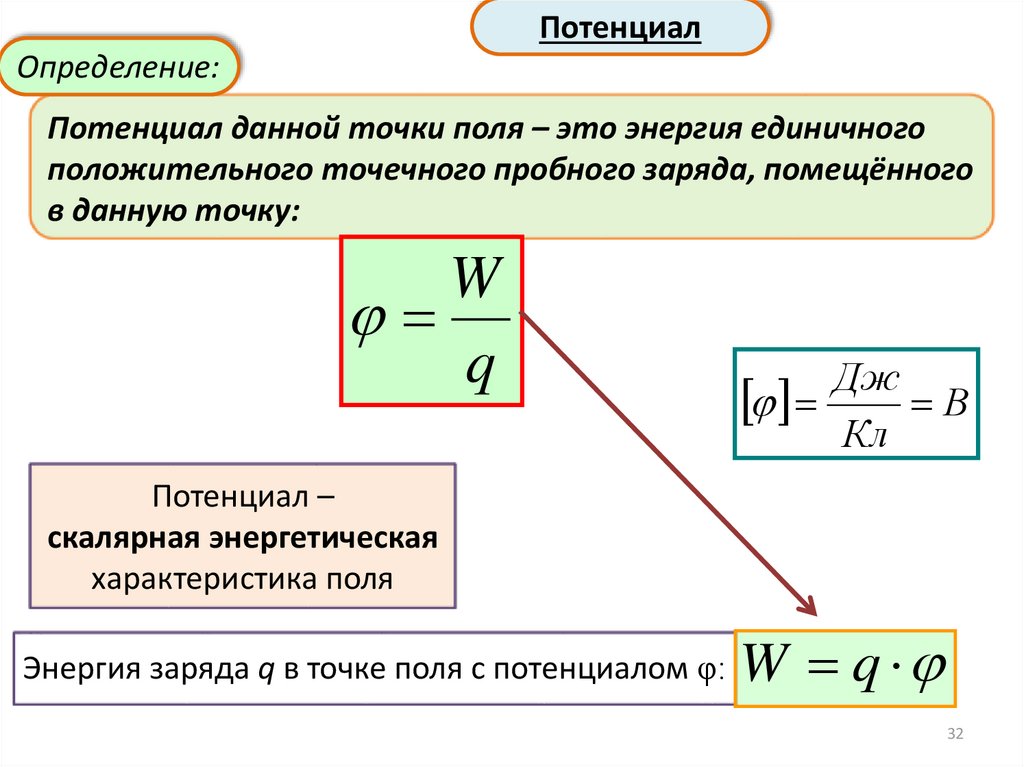
Потенциал
Определение:
Потенциал данной точки поля – это энергия единичного
положительного точечного пробного заряда, помещённого
в данную точку:
W
q
Дж
В
Кл
Потенциал –
скалярная энергетическая
характеристика поля
Энергия заряда q в точке поля с потенциалом φ:
W q
32

33.

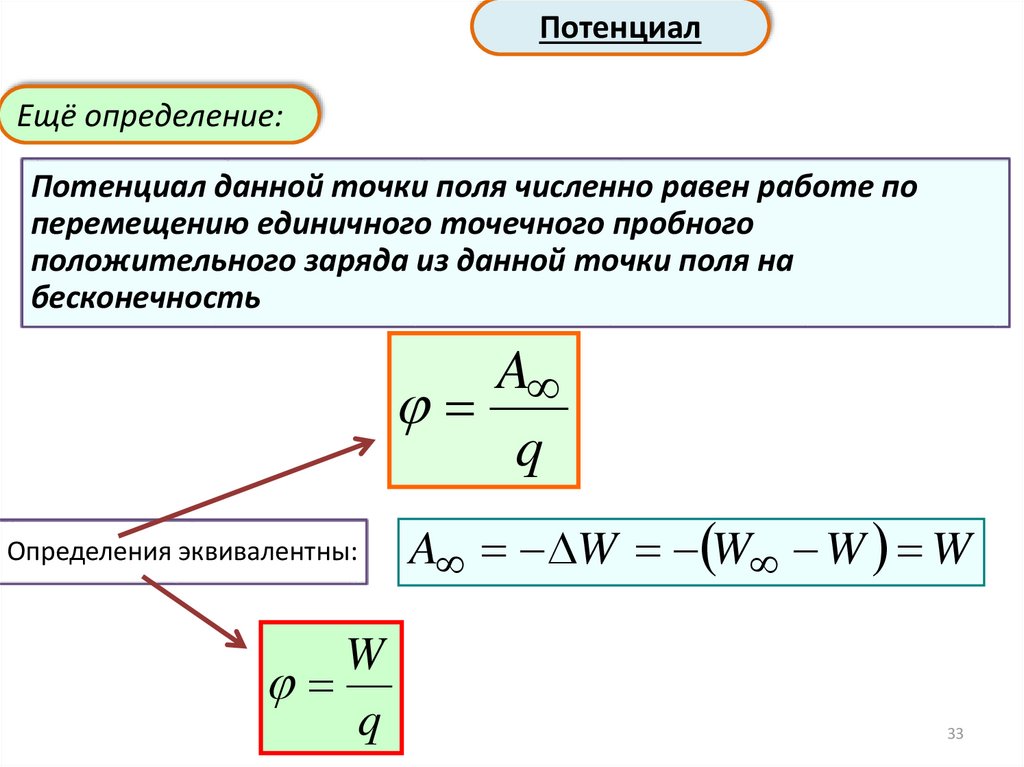
Потенциал
Ещё определение:
Потенциал данной точки поля численно равен работе по
перемещению единичного точечного пробного
положительного заряда из данной точки поля на
бесконечность
A
q
Определения эквивалентны:
W
q
A W W W W
33

34.

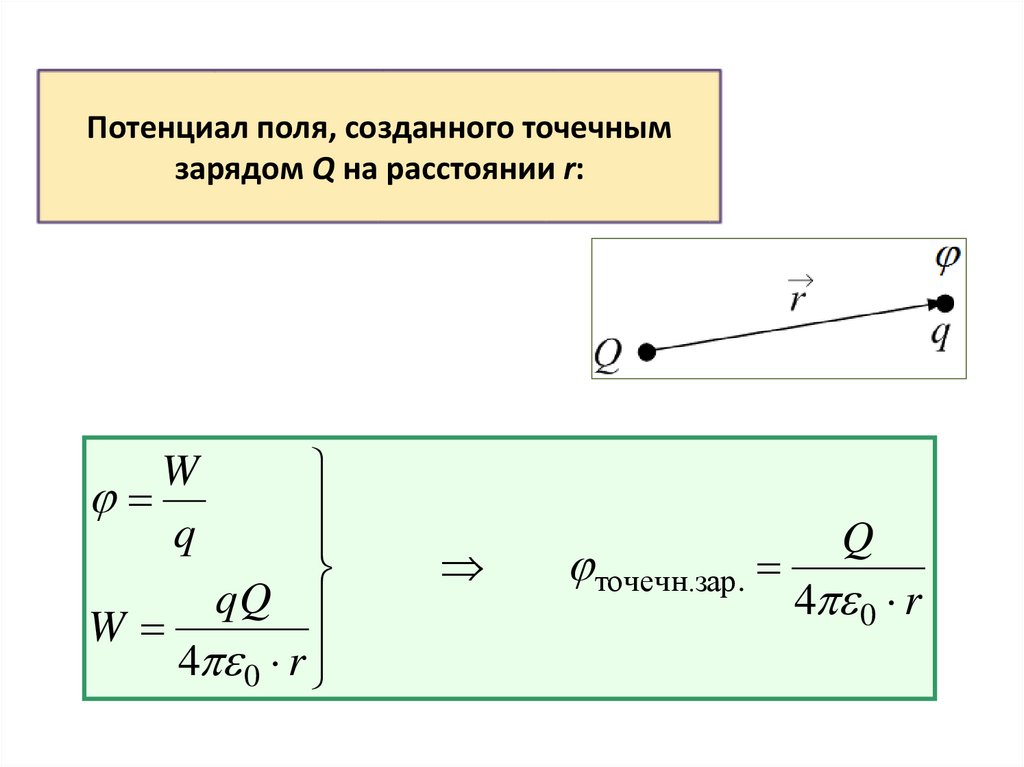
Потенциал поля, созданного точечным
зарядом Q на расстоянии r:
qQ
W
4 0 r
W
q
точечн.зар.
Q
4 0 r

35.

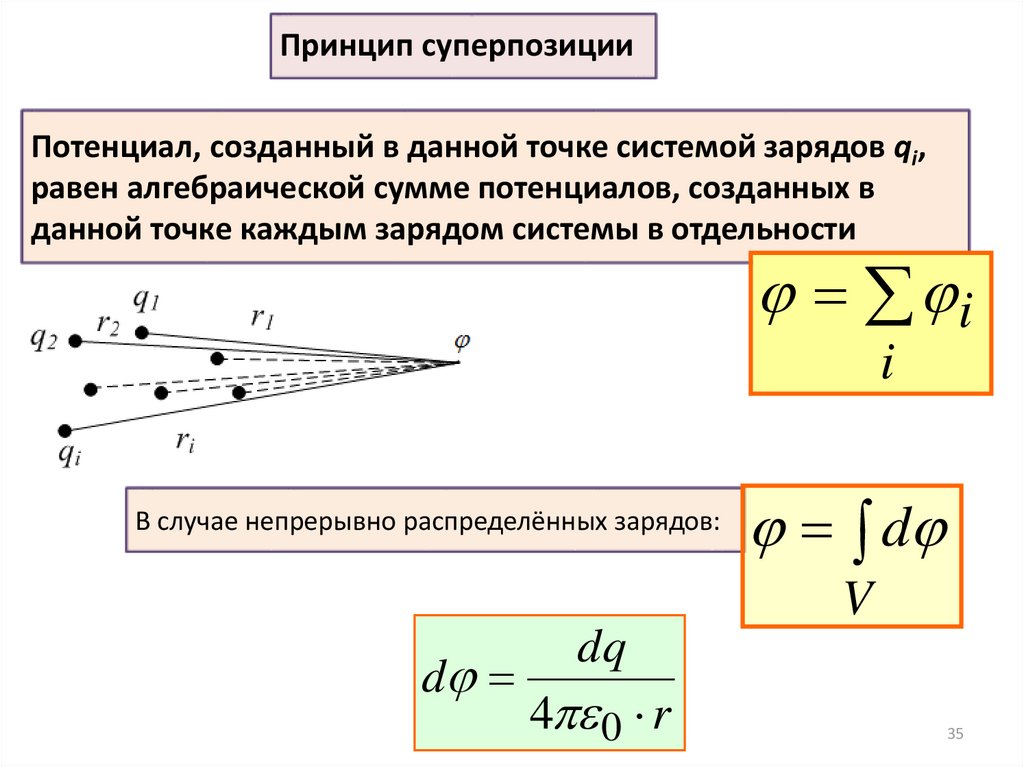
Принцип суперпозиции
Потенциал, созданный в данной точке системой зарядов qi,
равен алгебраической сумме потенциалов, созданных в
данной точке каждым зарядом системы в отдельности
i
i
В случае непрерывно распределённых зарядов:
d
V
d
dq
4 0 r
35

36.

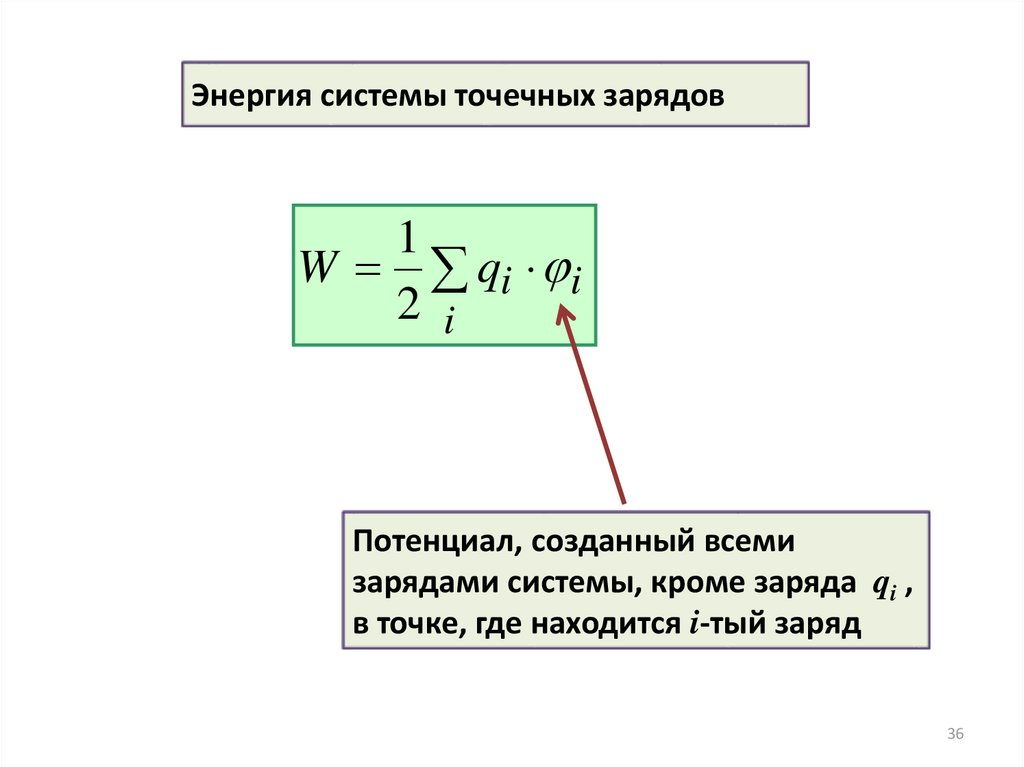
Энергия системы точечных зарядов
1
W qi i
2 i
Потенциал, созданный всеми
зарядами системы, кроме заряда qi ,
в точке, где находится i-тый заряд
36

37.

38.

Связь между напряженностью и потенциалом
Вектор напряжённости направлен в
сторону наибольшего УБЫВАНИЯ
потенциала
Для однородного поля:
E
x

39.

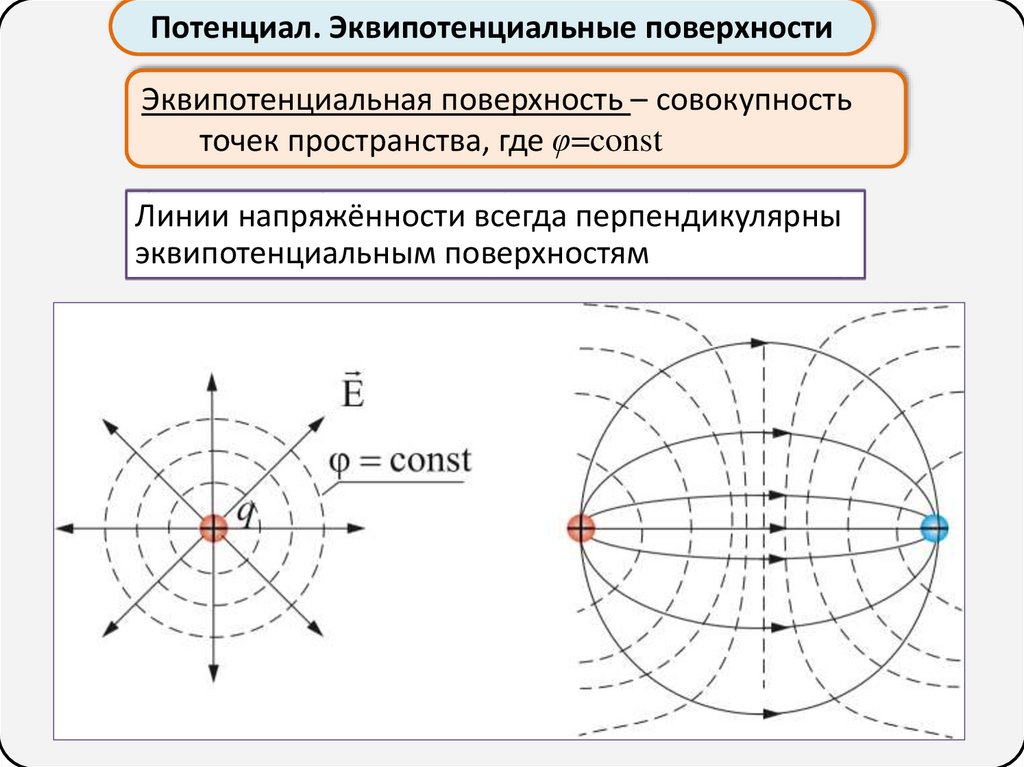
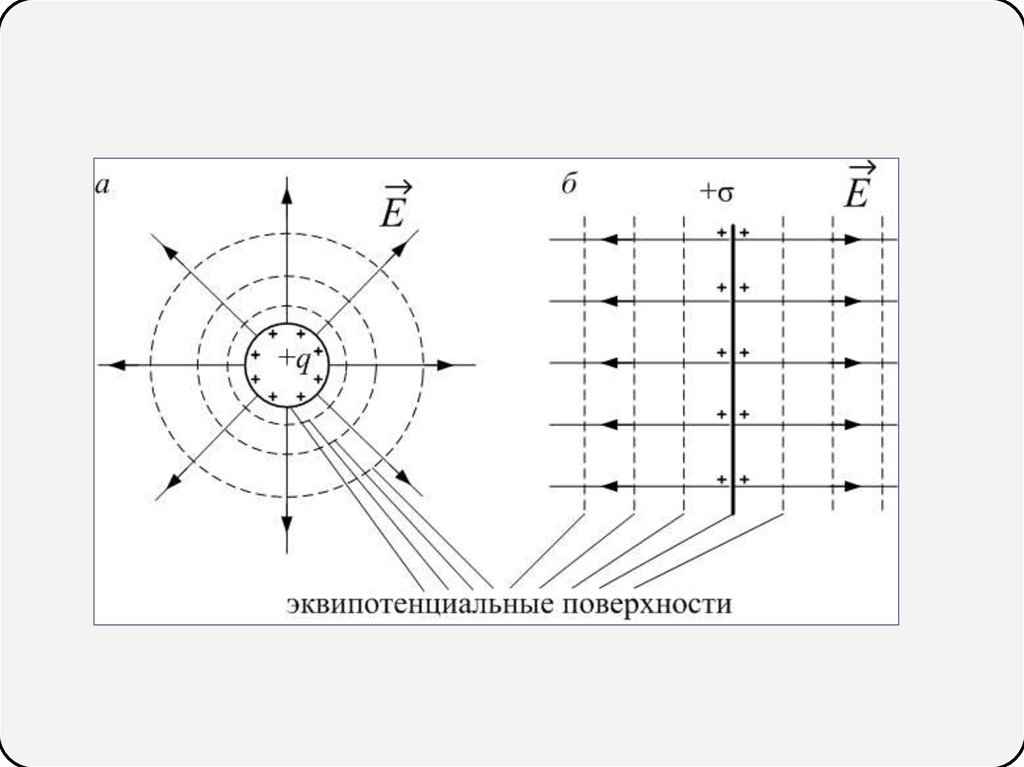
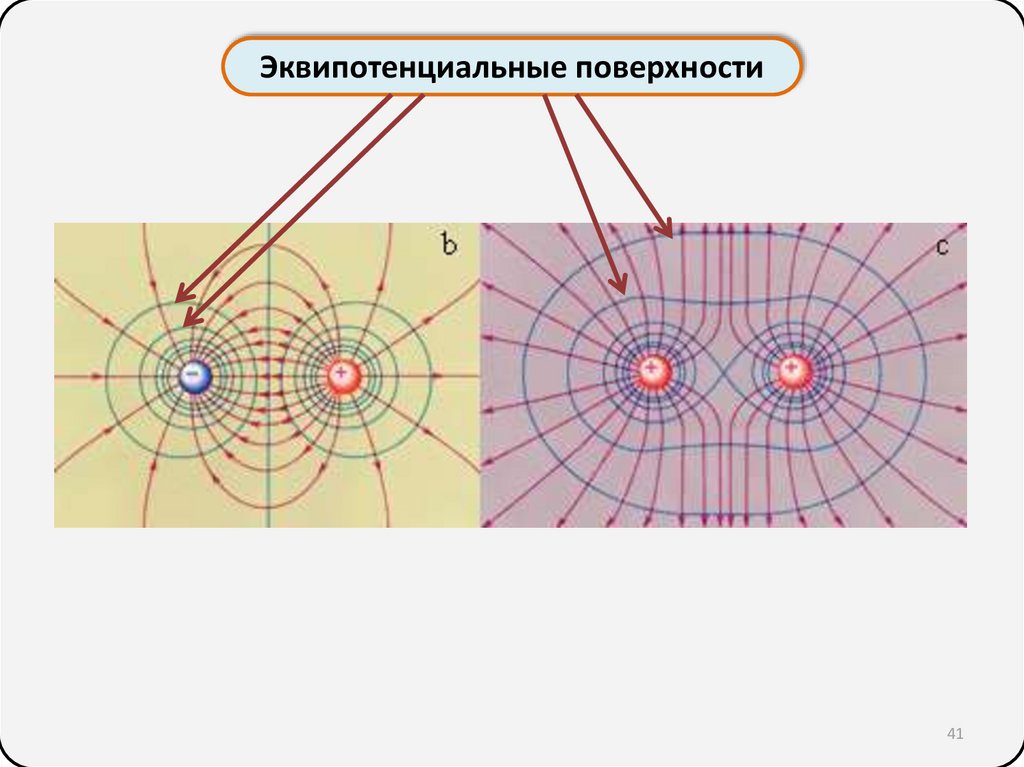
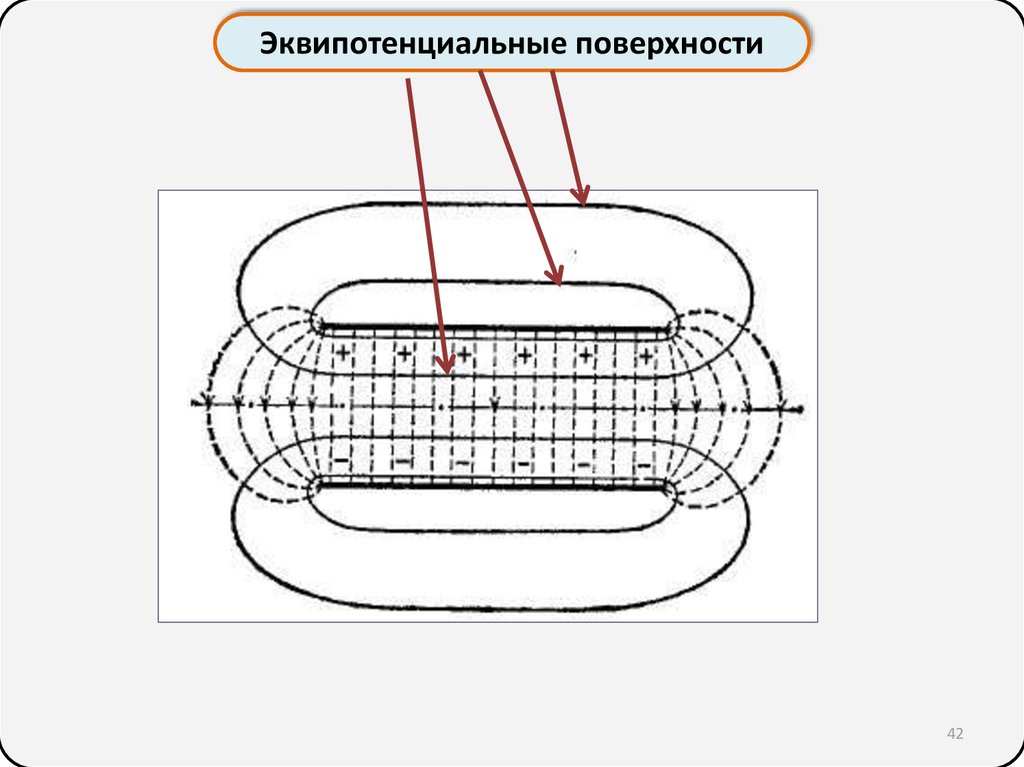
Потенциал. Эквипотенциальные поверхности
Эквипотенциальная поверхность – совокупность
точек пространства, где φ=const
Линии напряжённости всегда перпендикулярны
эквипотенциальным поверхностям
39

40.

41.

Эквипотенциальные поверхности
41

42.

Эквипотенциальные поверхности
42

43.

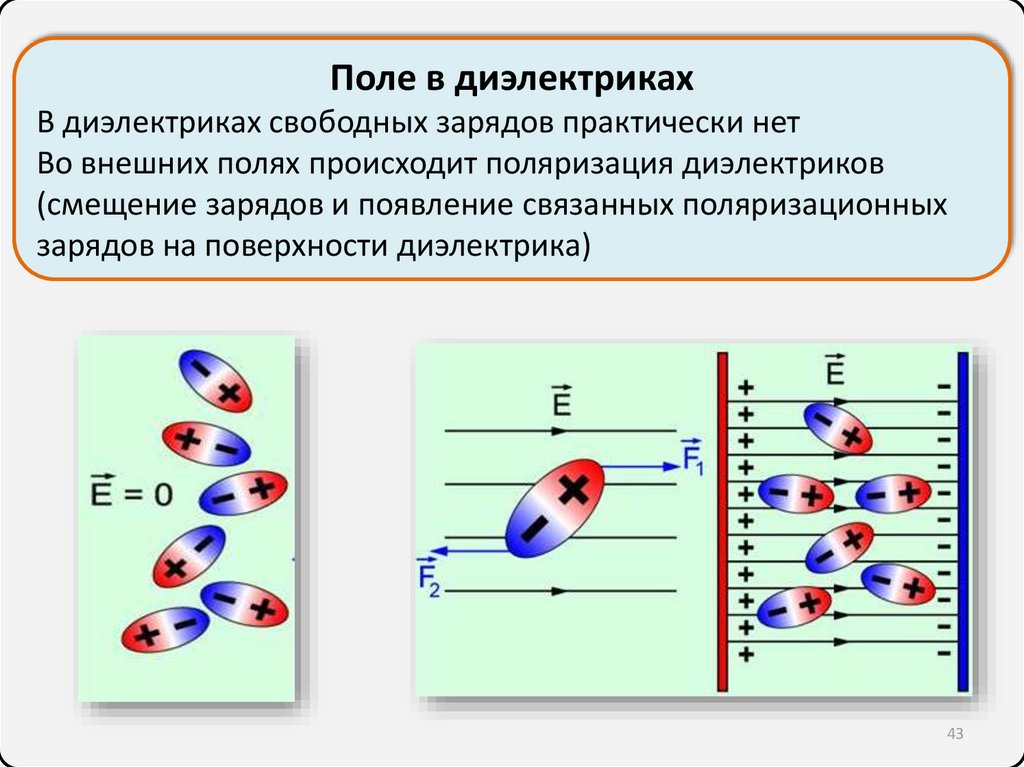
Поле в диэлектриках
В диэлектриках свободных зарядов практически нет
Во внешних полях происходит поляризация диэлектриков
(смещение зарядов и появление связанных поляризационных
зарядов на поверхности диэлектрика)
43

44.

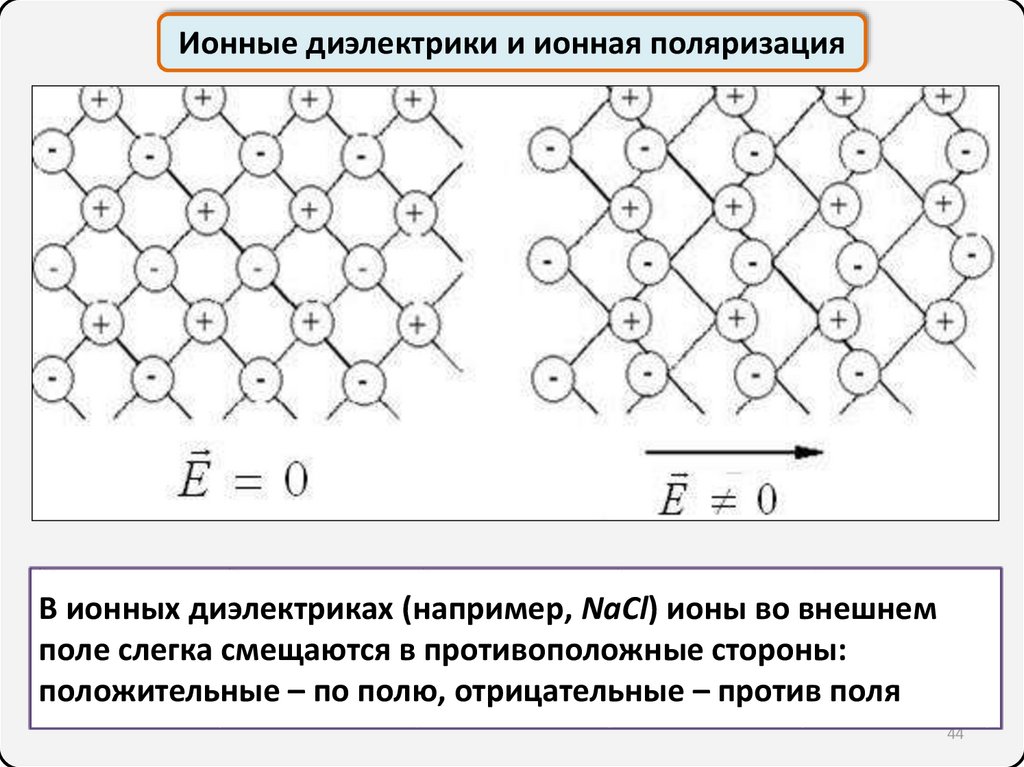
Ионные диэлектрики и ионная поляризация
В ионных диэлектриках (например, NaCl) ионы во внешнем
поле слегка смещаются в противоположные стороны:
положительные – по полю, отрицательные – против поля
44

45.

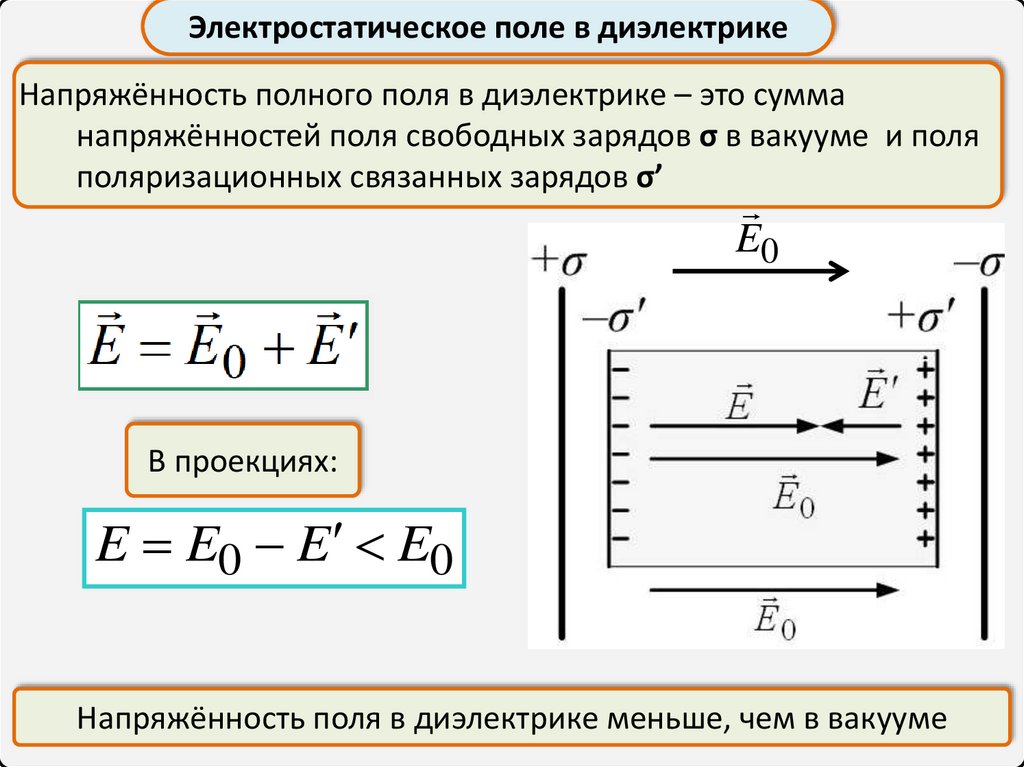
Электростатическое поле в диэлектрике
Напряжённость полного поля в диэлектрике – это сумма
напряжённостей поля свободных зарядов σ в вакууме и поля
поляризационных связанных зарядов σ’
E0
E E0 E
В проекциях:
E E0 E E0
Напряжённость поля в диэлектрике меньше, чем в вакууме

46.

Диэлектрическая проницаемость
E0
E
1
Диэлектрическая проницаемость показывает, во
сколько раз напряжённость электростатического
поля уменьшается в диэлектрике по сравнению с
вакуумом
Для вакуума по определению ε=1
В любом веществе поле может только ослабляться из-за
поляризации: ε>1
Для воды при 200С ε=81

47.

Резюме: формулы для поля в диэлектрике
F
E
q
4 0 r
2
q1q2
4 0 r 3
r
W
E
2 0
E
2 0 r
E
0
q1q2
4 0 r
q
4 0 r
свободн.
D
cos
dS
q
i
i
S
E cos dS
S
1
0 i
qiсвободн.
1
0
свободн.
связ.
(
q
q
)
i
i
i
47

48.

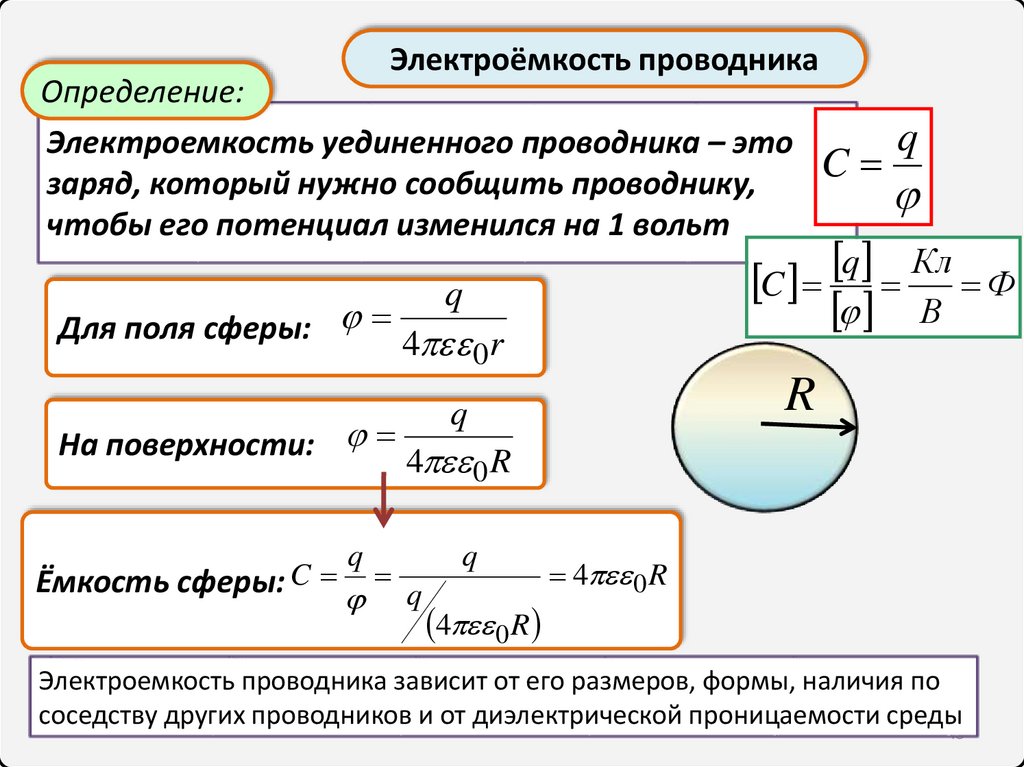
Электроёмкость проводника
Определение:
Электроемкость уединенного проводника – это
заряд, который нужно сообщить проводнику,
чтобы его потенциал изменился на 1 вольт
Для поля сферы: 4 r
0
R
q
На поверхности: 4 R
0
q
q
q
4 0 R
C q Кл Ф
В
q
Ёмкость сферы: C
C
q
4 0 R
Электроемкость проводника зависит от его размеров, формы, наличия по
соседству других проводников и от диэлектрической проницаемости среды
48

49.

Конденсаторы
Если недалеко от заряженного проводника находится другой проводник, то
из-за явления электростатической индукции ёмкость проводника меняется
(возрастает)
Конденсатор – это два проводника (две обкладки),
находящихся вблизи друг друга
Плоский
Сферический
Цилиндрический
49

50.

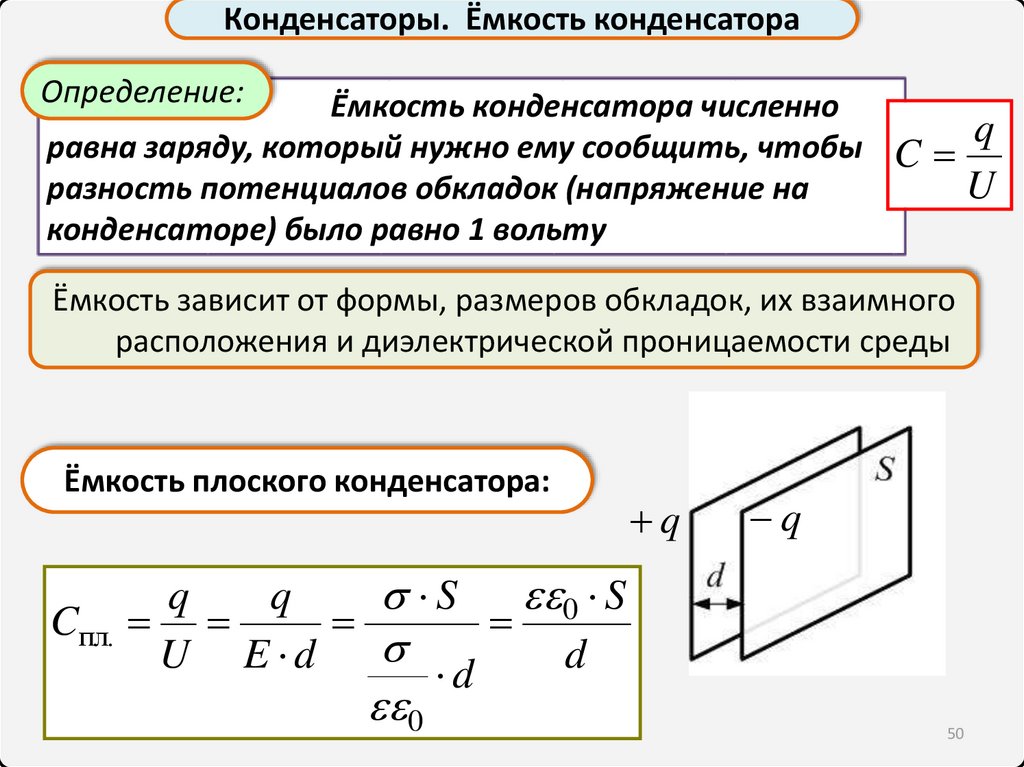
Конденсаторы. Ёмкость конденсатора
Определение:
Ёмкость конденсатора численно
равна заряду, который нужно ему сообщить, чтобы C q
U
разность потенциалов обкладок (напряжение на
конденсаторе) было равно 1 вольту
Ёмкость зависит от формы, размеров обкладок, их взаимного
расположения и диэлектрической проницаемости среды
Ёмкость плоского конденсатора:
Cпл.
q q
q
q
S 0 S
U E d
d
d
0
50

51.

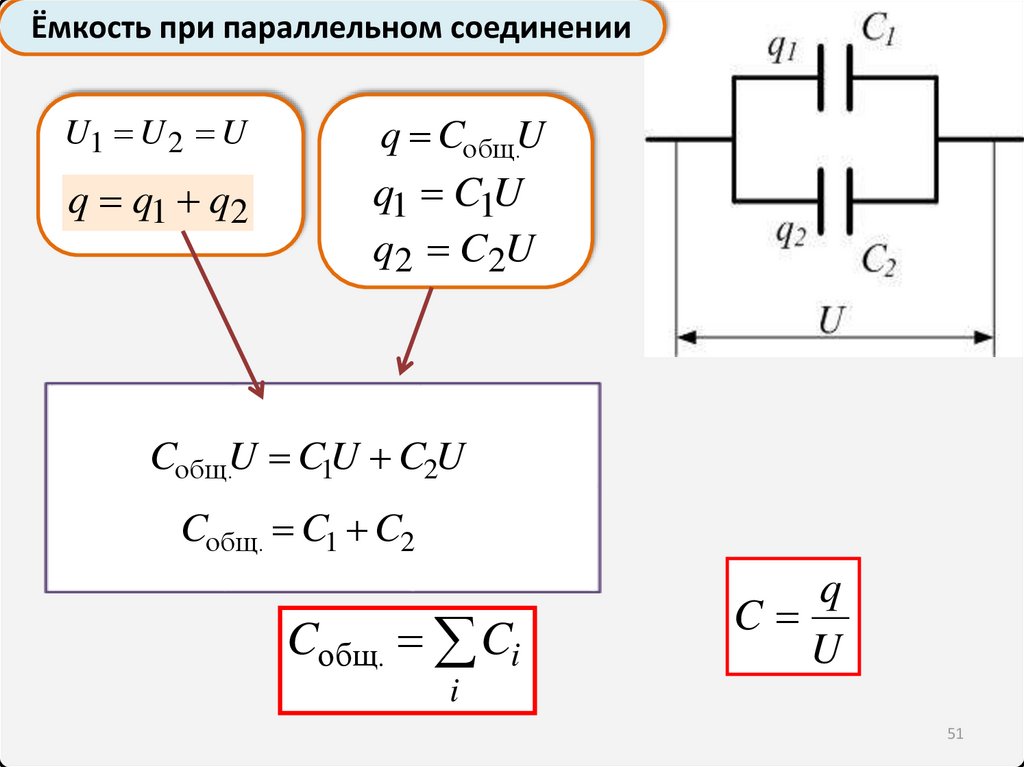
Ёмкость при параллельном соединении
U1 U 2 U
q q1 q2
q Cобщ.U
q1 C1U
q2 C2U
Cобщ.U C1U C2U
Cобщ. C1 C2
Cобщ. Ci
q
C
U
i
51

52.

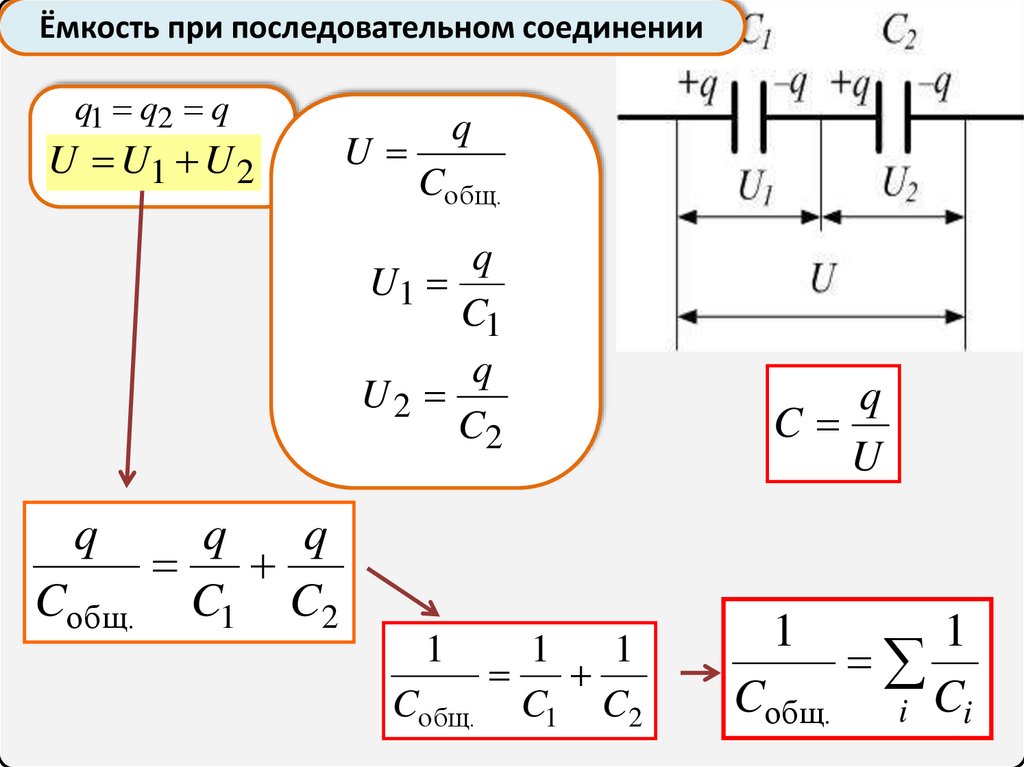
Ёмкость при последовательном соединении
q1 q2 q
U U1 U 2
U
q
Cобщ.
q
U1
C1
q
U2
C2
q
Cобщ.
q
q
C1 C2
1
Cобщ.
1
1
C1 C2
q
C
U
1
Cобщ.
1
i Ci
52

53.

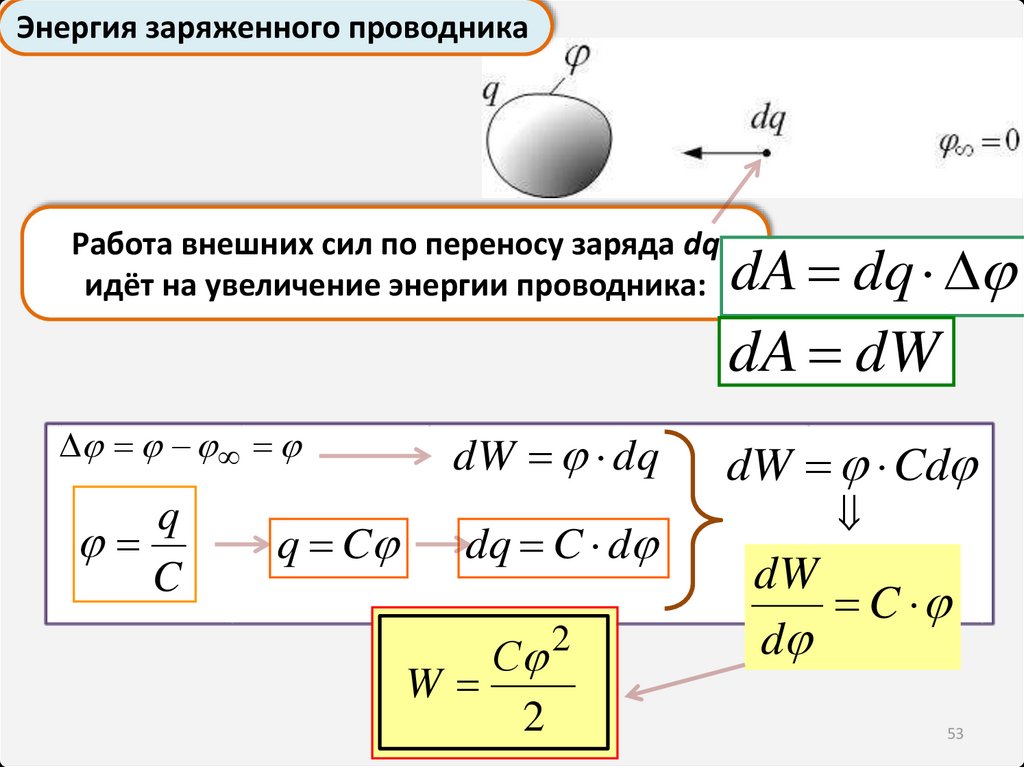
Энергия заряженного проводника
Работа внешних сил по переносу заряда dq
идёт на увеличение энергии проводника:
q
C
q C
dW dq
dq C d
С 2
W
2
dA dq
dA dW
dW Cd
dW
C
d
53

54.

Энергия заряженного проводника
С 2
W
2
q C
q
C
2
q
C
2
2
C
Cq
C
W
2
2
2
2C
q2
W
2C
C
C q
W
2
2
2 W q
2
2
Энергия заряженного конденсатора:
2
2
СU
qU q
W
2
2
2C
54