Похожие презентации:
Молекулярно-кинетическая теория (МКТ) и термодинамика (лекция 5)
1.
ВоГУЛекция 5
Молекулярно-кинетическая теория
(МКТ) и
термодинамика
Кузина Л.А.,
к.ф.-м.н., доцент
2020 г.
1
2.
23.
Молекулярная физика изучает строение и свойства веществаМолекулярно-кинетическая теория (МКТ) исходит из
молекулярно-кинетических представлений:
1) все вещества состоят из молекул (атомов);
2) молекулы (атомы) находятся в непрерывном движении;
3) молекулы взаимодействуют между собой.
Экспериментальные доказательства
молекулярно-кинетических представлений:
1) Броуновское движение
2) диффузия
4.
Методы исследований:1) статистический
метод основан на том, что свойства
макросистем, состоящих из большого
числа микрочастиц, определяются
усреднёнными значениями
характеристик этих микрочастиц
(например, скоростей, энергий)
2) термодинамический
Термодинамика изучает общие свойства
макросистем, находящихся в состоянии
термодинамического равновесия, и процессы
перехода между состояниями.
В основе термодинамики лежат 3 закона (начала)
термодинамики, основанных на опыте.
5.
Основные понятия (определения)Система – это любая мысленно выделенная совокупность тел
Окружающая среда
– это всё, что не входит в систему
Параметры
(термодинамические переменные) – переменные,
определеляющие состояние системы в
термодинамике – температура, давление, объём
Экстенсивные
зависят от количества вещества (V, m,
Интенсивные
не зависят от количества вещества (T, p)
Уравнение состояния – уравнение вида: f(p,V,T)=0,
связывающее параметры системы
m
)
6.
Молекулярно-кинетическая теория идеального газа.Уравнение состояния
Газ идеальный, если
1) Собственным объёмом молекул можно пренебречь по
сравнению с объёмом сосуда.
2) Взаимодействием молекул между собой можно
пренебречь.
3) Столкновения молекул между собой и со стенками сосуда
– абсолютно упругие.
При нормальных условиях ( T=273 К, p= 105 Па)
газ можно считать идеальным
7.
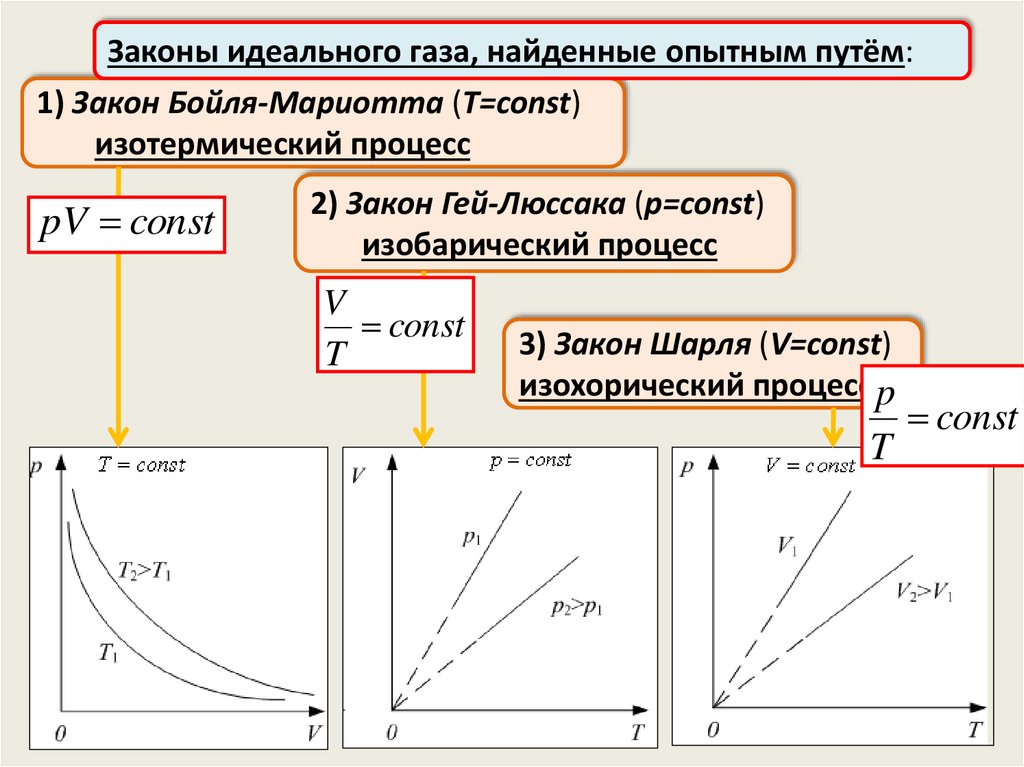
Законы идеального газа, найденные опытным путём:1) Закон Бойля-Мариотта (T=const)
изотермический процесс
pV const
2) Закон Гей-Люссака (p=const)
изобарический процесс
V
const
T
3) Закон Шарля (V=const)
изохорический процесс p
T
const
8.
Уравнение состояния идеального газаОбъединённый газовый закон обобщает все три
закона:
pV const
V
const
T
p V
const
T
p V
m
RT
Уравнение Менделеева-Клапейрона –
уравнение состояния идеального газа
p
const
T
9.
Уравнение состояния идеального газаЗакон Авогадро: В одном моле любого вещества содержится
одинаковое число молекул (атомов), равное числу Авогадро NА
m RT m0 N RT N R
p
T n k T
V
m0 N А V
V NА
m m0 N масса
m0 N А молярная масса
p V
m
RT
p n k T
R
k
постоянная
NА
Больцмана
N
n
V
концентрация
10.
Давление смеси газовПарциальное давление – это давление, которое оказывал
бы данный газ в отсутствие других газов при тех же условиях
Закон Дальтона: давление смеси газов равно сумме
парциальных давлений всех входящих в смесь газов:
p pi
Доказательство:
i
p n k T ni kT ni kT pi
i
i
i
Закон Паскаля: давление в любой точке покоящегося газа
одинаково по всем направлениям и одинаково передаётся
по всему объёму
11.
Основное уравнение молекулярно-кинетической теории(МКТ)
Давление газа на стенку – результат передачи стенке импульса
молекулами при упругих соударениях со стенкой
Предположения:
1) все молекулы имеют
одинаковые скорости v
2) молекулы могут двигаться
только в трёх взаимно
перпендикулярных
направлениях – либо
параллельно стенке, либо
перпендикулярно ей
1
6
12.
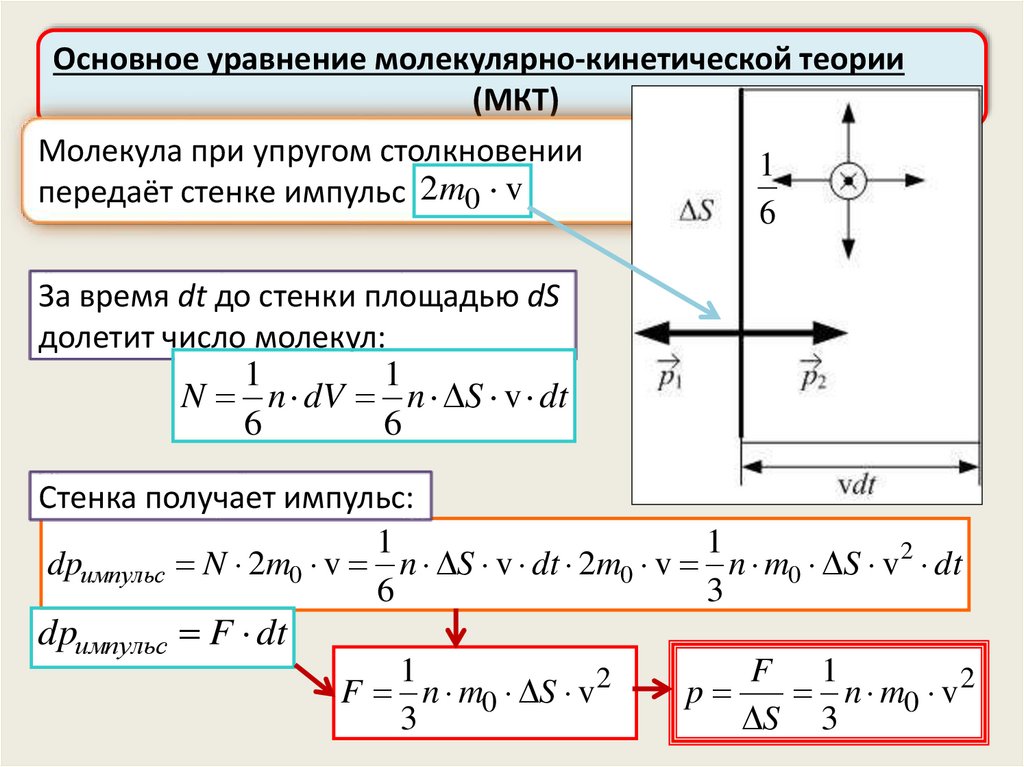
Основное уравнение молекулярно-кинетической теории(МКТ)
Молекула при упругом столкновении
1
передаёт стенке импульс 2m0 v
6
За время dt до стенки площадью dS
долетит число молекул:
1
1
N n dV n S v dt
6
6
Стенка получает импульс:
1
1
dpимпульс N 2m0 v n S v dt 2m0 v n m0 S v2 dt
6
3
dpимпульс F dt
1
F n m0 S v2
3
F 1
p
n m0 v 2
S 3
13.
Основное уравнение молекулярно-кинетической теории (МКТ)1
p n m0 v 2
3
1
2
p n m0 vкв.
3
Средняя квадратичная
скорость
По определению:
vкв.
m N m0
n m0
V
V
1
2
p vкв.
3
1
2
p n m0 vкв.
3
p n k T
2
m0 vкв.
E
2
Средняя энергия
поступательного
движения молекул
N
2
v
i
i
N
3kT
3RT
vкв.
m0
1
2
n m0 vкв.
n k T
3
1
2
m0 vкв.
k T
3
2
p n E
3
Основное уравнение МКТ
для давления
14.
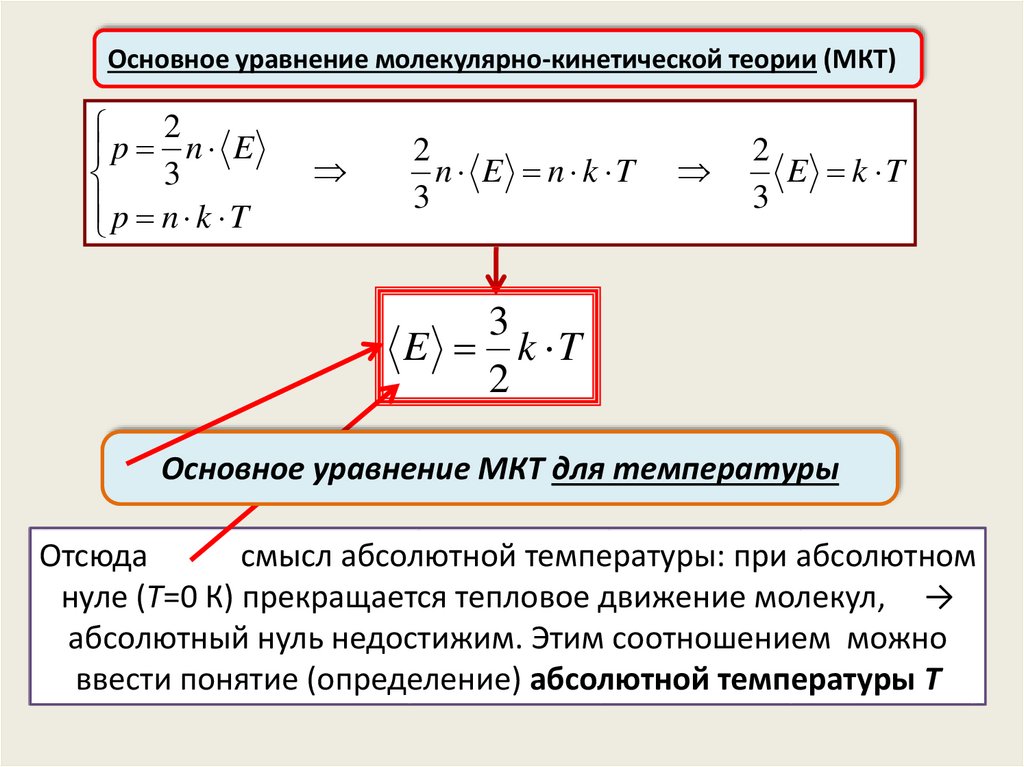
Основное уравнение молекулярно-кинетической теории (МКТ)2
p n E
3
p n k T
2
n E n k T
3
2
E k T
3
3
E k T
2
Основное уравнение МКТ для температуры
Отсюда
смысл абсолютной температуры: при абсолютном
нуле (T=0 К) прекращается тепловое движение молекул, →
абсолютный нуль недостижим. Этим соотношением можно
ввести понятие (определение) абсолютной температуры T
15.
Теорема о равнораспределении энергии по степеням свободыНа любую степень свободы приходится в среднем
одинаковая энергия, равная
k T
E1
2
Число степеней свободы i
равно числу независимых
координат, однозначно
определяющих положение
тела (или молекулы) в
пространстве
16.
Число степеней свободыОдноатомные:
i =iпост=3 (3 координаты - x, y, z)
Двухатомные:
i=iпост+iвр.=3+2=5
(3 координаты центра масс и
2 угловых;
одна из осей неактивна)
Модель
«жёсткая гантель»
Многоатомные нелинейные и абсолютно
твёрдое тело:
i=iпост+iвр.=3+3=6
(3 координаты центра масс и 3 угловых)
iэфф.=iпост+iвр. +2iкол=3+2+2.1=7
2 вида энергии при колебаниях:
кинетическая и потенциальная
17.
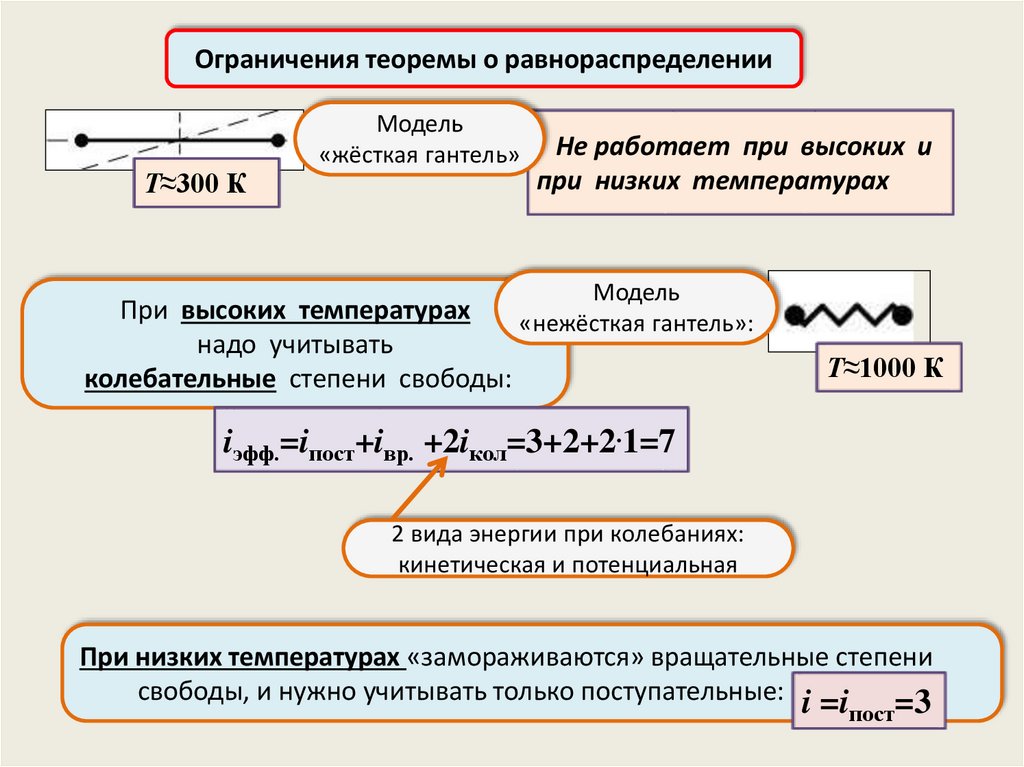
Ограничения теоремы о равнораспределенииТ≈300 К
Модель
«жёсткая гантель»
При высоких температурах
надо учитывать
колебательные степени свободы:
Не работает при высоких и
при низких температурах
Модель
«нежёсткая гантель»:
Т≈1000 К
iэфф.=iпост+iвр. +2iкол=3+2+2.1=7
2 вида энергии при колебаниях:
кинетическая и потенциальная
При низких температурах «замораживаются» вращательные степени
свободы, и нужно учитывать только поступательные: i =i
=3
пост
18.
Внутренняя энергия идеального газаНа одну степень свободы:
k T
E1
2
Средняя энергия молекулы с i степенями свободы:
Eмол.
i
k T
2
Суммарная энергия N молекул идеального газа:
N i k T N А k i T i N А k T
i
U N E1
RT
2
2
2
2
Внутренняя энергия идеального газа – суммарная кинетическая энергия всех
молекул; потенциальная энергия взаимодействия молекул не учитывается
Внутренняя энергия U – суммарная кинетическая и потенциальная
энергия всех частиц: электронов в атомах, нуклонов в ядрах атомов и т.д.
Внутренняя энергия не включает энергию движения тела как
целого (движения центра масс и вращения тела как целого) и
потенциальную энергию тела во внешних полях
19.
ТермодинамикаТермодинамика изучает общие свойства макросистем, находящихся в
состоянии термодинамического равновесия, и процессы перехода между
состояниями. Термодинамика позволяет понять, какие процессы
возможны, а какие – нет.
Отвлекаясь от движения тела как целого, термодинамика сосредотачивает
внимание на изменениях внутреннего состояния тела, состояния
термодинамической системы
На основе общих принципов механики пытались установить связь между
молекулярным движением и тепловыми явлениями
Термодинамику пытались свести к механике
Это принципиально невозможно
Законы Ньютона обратимы во времени
Тепловые процессы необратимы: теплота переходит от горячего к холодному,
но не наоборот
Ньютоновская механика принципиально не может объяснить
необратимость процессов
Сведение термодинамики к механике оказывается невозможным
20.
Предмет и задачи термодинамикиПример: греем газ в закрытом сосуде, приведя его в соприкосновение с
нагретым телом. Увеличивается энергия газа; он при расширении может
совершить механическую работу
При теплообмене передача энергии происходит на микроскопическом
уровне, при столкновениях молекул. Результат каждого отдельного
столкновения предсказать невозможно. Но в среднем, с
макроскопической точки зрения, при соударении энергичных молекул
нагретого тела со стенками сосуда с газом энергия переходит от
нагретого тела к газу. В результате тепловая энергия обязательно
перетекает от горячего тела к газу
Теплота представляет собой особую форму движения материи.
Хотя теплота и связана с молекулярным механическим движением, но этим
не исчерпывается ее сущность
В механике переменными являются координаты и импульсы (скорости)
частиц.
В термодинамике такое описание оказалось неприемлемым. В число
переменных (параметров) в термодинамике потребовалось ввести
температуру
Температура определяет направление перехода теплоты, то есть
выступает как мера нагретости тела
21.
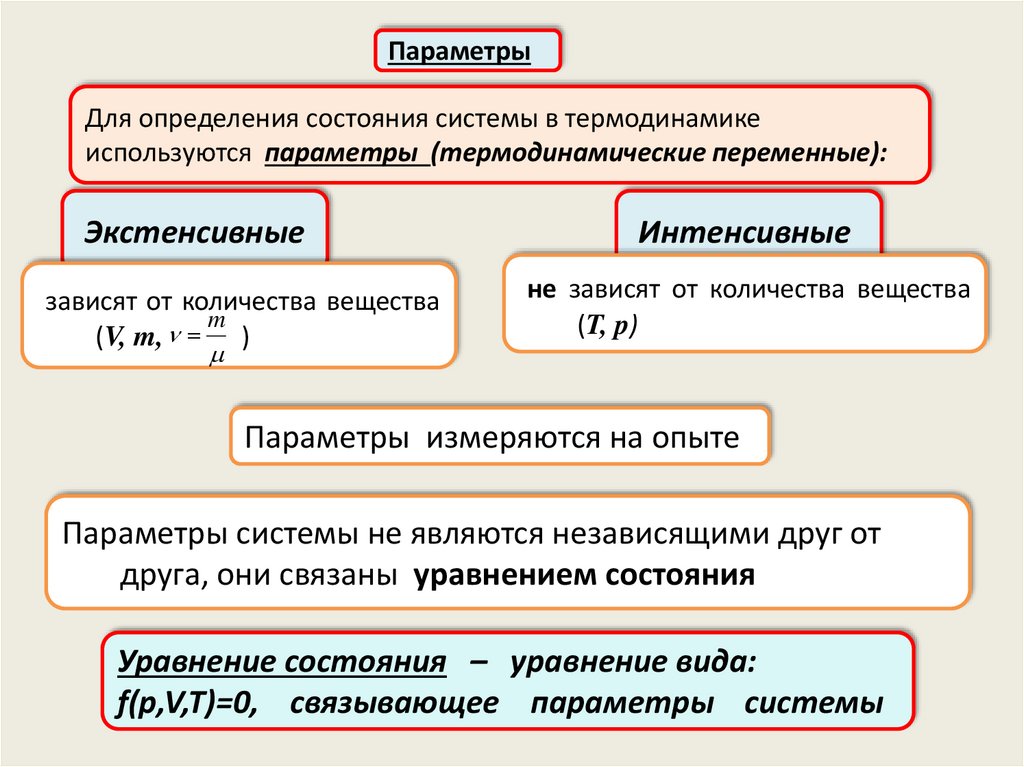
ПараметрыДля определения состояния системы в термодинамике
используются параметры (термодинамические переменные):
Экстенсивные
зависят от количества вещества
m
(V, m, )
Интенсивные
не зависят от количества вещества
(T, p)
Параметры измеряются на опыте
Параметры системы не являются независящими друг от
друга, они связаны уравнением состояния
Уравнение состояния – уравнение вида:
f(p,V,T)=0, связывающее параметры системы
22.
В основе термодинамики лежат основанные на опытезаконы (начала) термодинамики
В термодинамике нет моделей, теоретических предположений о строении
вещества или о механизме процессов.
Свойства вещества – теплоёмкость, температурные коэффициенты
объёмного и линейного расширения, и т.д. – определяются из опыта
Закон теплового равновесия
(нулевое начало термодинамики)
Понятие теплового равновесия является одним из главнейших
исходных термодинамических понятий.
Опыт показывает, что если системы 1 и 2 находятся в тепловом
равновесии с системой 3, то то системы 1 и 2 будут также в тепловом
равновесии друг с другом.
Значение этого закона заключается в том, что он приводит к выводу о
существовании температуры как характеристики теплового равновесия
системы.
Температура есть присущая каждому состоянию равновесия
интенсивная величина
23.
Внутренняя энергияОдно из важных понятий – внутренняя энергия системы U.
Внутренняя энергия тела – это полная энергия тела, за исключением
кинетической энергии движения тела как целого (движения центра масс
и вращения тела как целого) и потенциальной энергии тела во внешних
полях
Внутренняя энергия системы – это функция
состояния, то есть однозначно определяется
состоянием системы.
Изменение внутренней энергии системы в какомлибо процессе не зависит от пути перехода, а только
от начального и конечного сотояния; а в замкнутом
процессе, когда система возвращается в исходное
состояние, изменение внутренней энергии равно
нулю
24.
Первое начало термодинамикиВнутреннюю энергию системы можно изменить за счёт:
1) совершения над системой работы;
2) сообщения системе теплоты:
dU Q Aвнешних сил
U Q Aвнешних сил
A Aвнешних сил
Q A dU
Q A U
Количество теплоты, сообщённое системе, идёт на
приращение её внутренней энергии и на работу системы
против внешних сил
25.
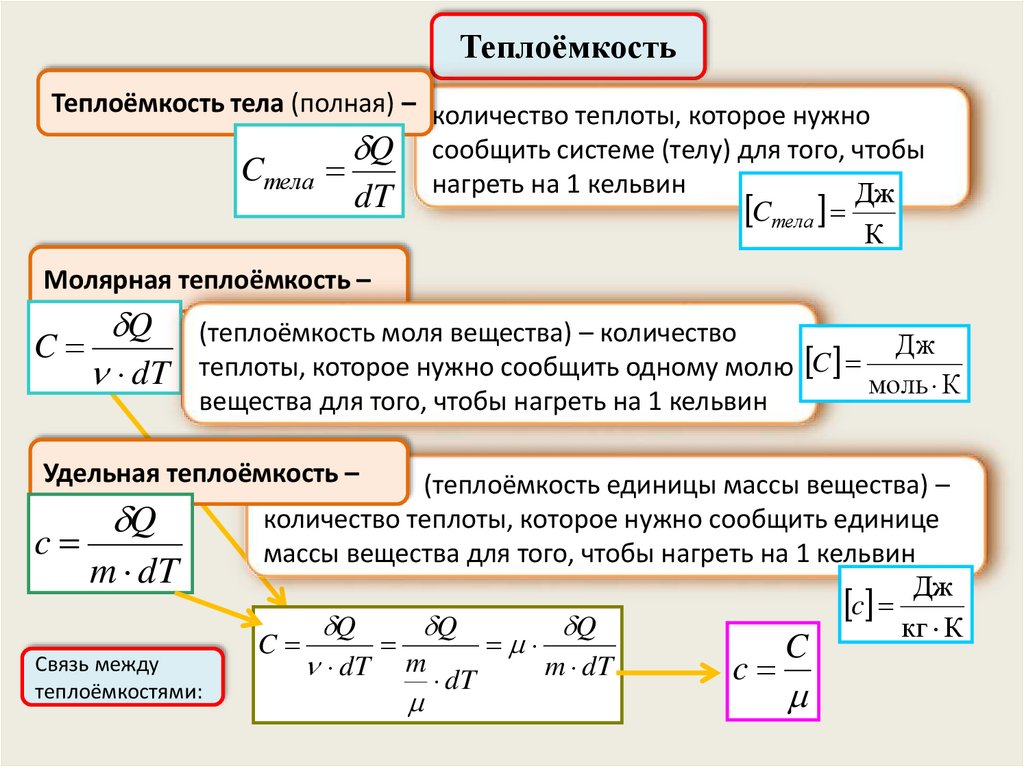
ТеплоёмкостьТеплоёмкость тела (полная) – количество теплоты, которое нужно
Q сообщить системе (телу) для того, чтобы
Cтела
dT нагреть на 1 кельвин
Cтела Дж
К
Молярная теплоёмкость –
C
Q
dT
(теплоёмкость моля вещества) – количество
Дж
C
теплоты, которое нужно сообщить одному молю
моль К
вещества для того, чтобы нагреть на 1 кельвин
Удельная теплоёмкость –
c
Q
m dT
Связь между
теплоёмкостями:
(теплоёмкость единицы массы вещества) –
количество теплоты, которое нужно сообщить единице
массы вещества для того, чтобы нагреть на 1 кельвин
c Дж
Q
Q
Q
кг К
C
C
dT m dT
m dT
c
26.
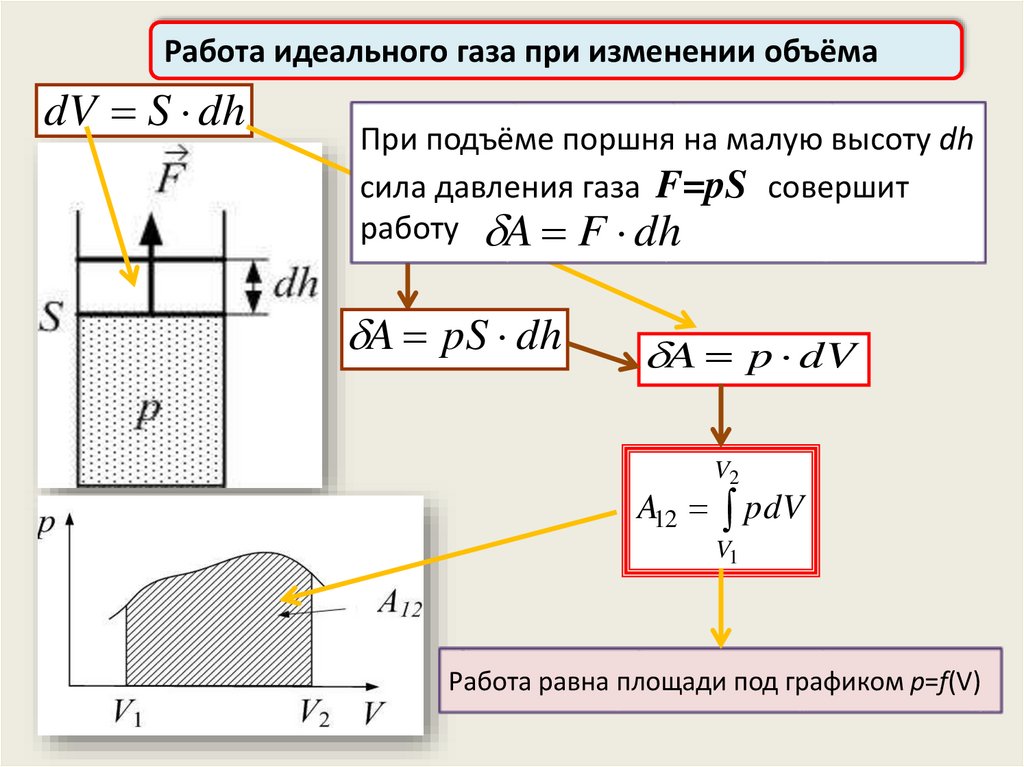
Работа идеального газа при изменении объёмаdV S dh
При подъёме поршня на малую высоту dh
сила давления газа F=pS совершит
работу A
A FF dh
dh
A pS dh
A p dV
A12
V2
pdV
V1
Работа равна площади под графиком p=f(V)
27.
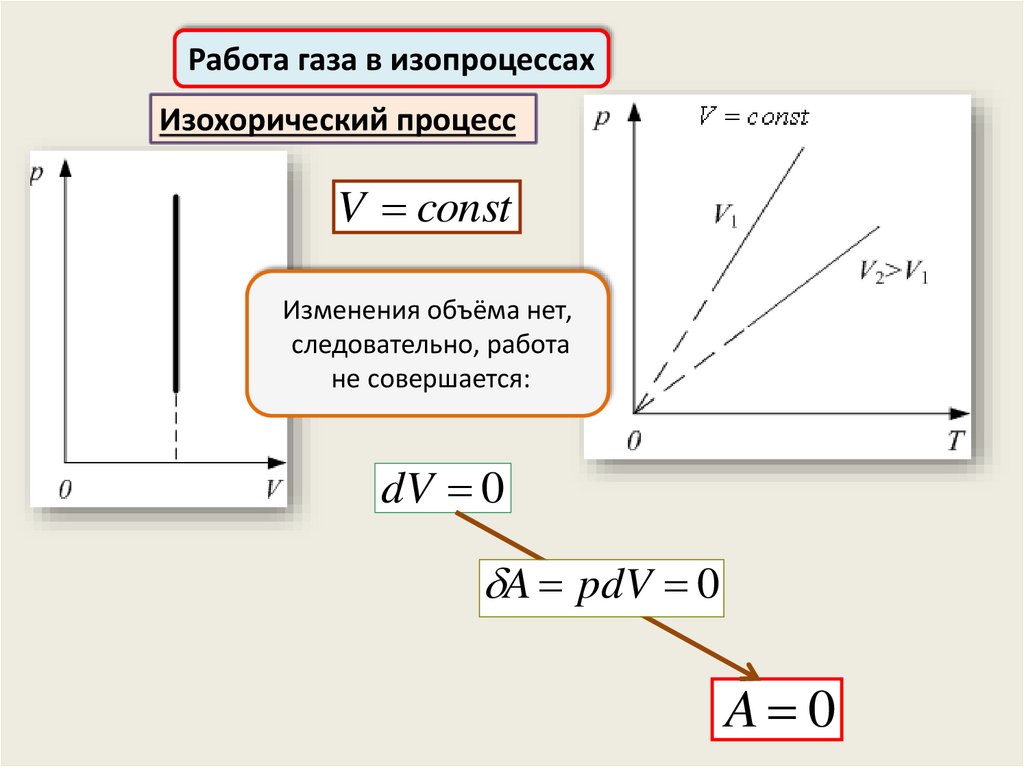
Работа газа в изопроцессахИзохорический процесс
V const
Изменения объёма нет,
следовательно, работа
не совершается:
dV 0
A pdV 0
A 0
28.
Работа газа в изопроцессахИзобарический процесс
A12
V2
V2
V1
V1
pdV p dV p V2 V1
A12 p V
p V1 RT1
p V2 RT2
A12 p V2 V1 pV2 pV1
Универсальная газовая
постоянная R численно
равна работе одного моля
идеального газа при
изобарном нагревании на
1 кельвин
A12 RT2 RT1 R T2 T1
A12 R T
A12
R
T
R
A
dT
29.
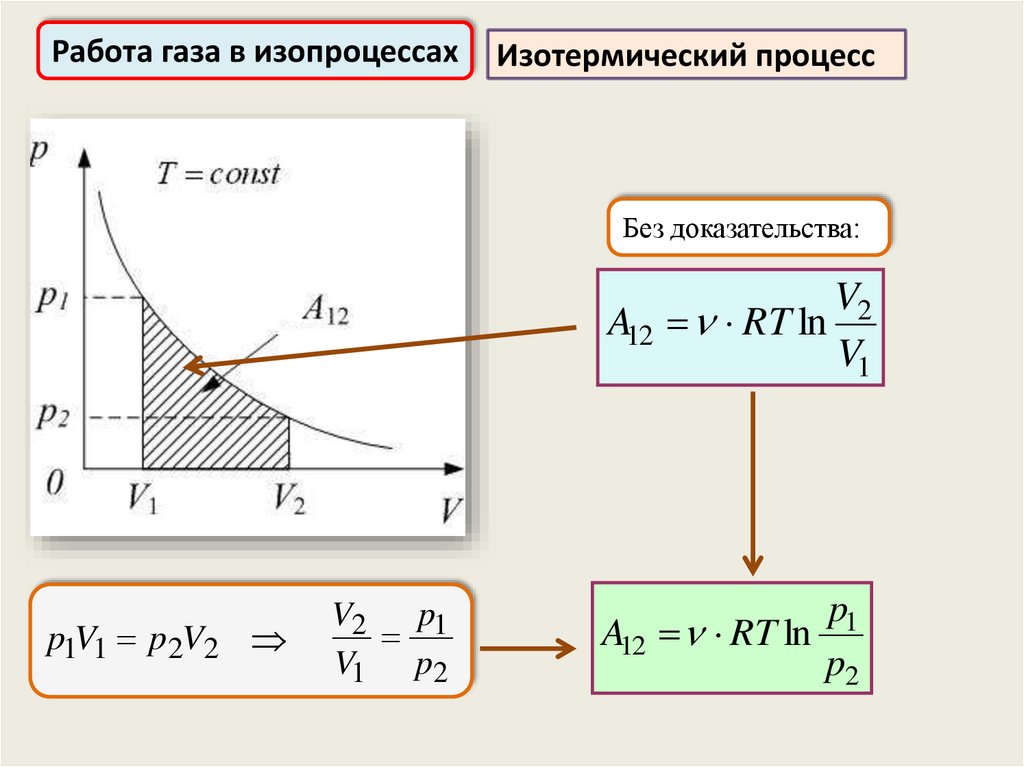
Работа газа в изопроцессахИзотермический процесс
Без доказательства:
V2
A12 RT ln
V1
p1V1 p2V2
V2 p1
V1 p2
p1
A12 RT ln
p2
30.
Применение первого начала термодинамики кизопроцессам с идеальным газом
Q A dU
1) Изохорический процесс
i
U RT
2
V const A 0 Q dU
A 0
i
Q dU R dT
2
Молярная теплоёмкость при постоянном объёме:
Q
dU
CV
dT dT
В интегральном виде:
i
CV R
2
i
Q U CV T R T
2
31.
Применение первого начала термодинамики кизопроцессам с идеальным газом
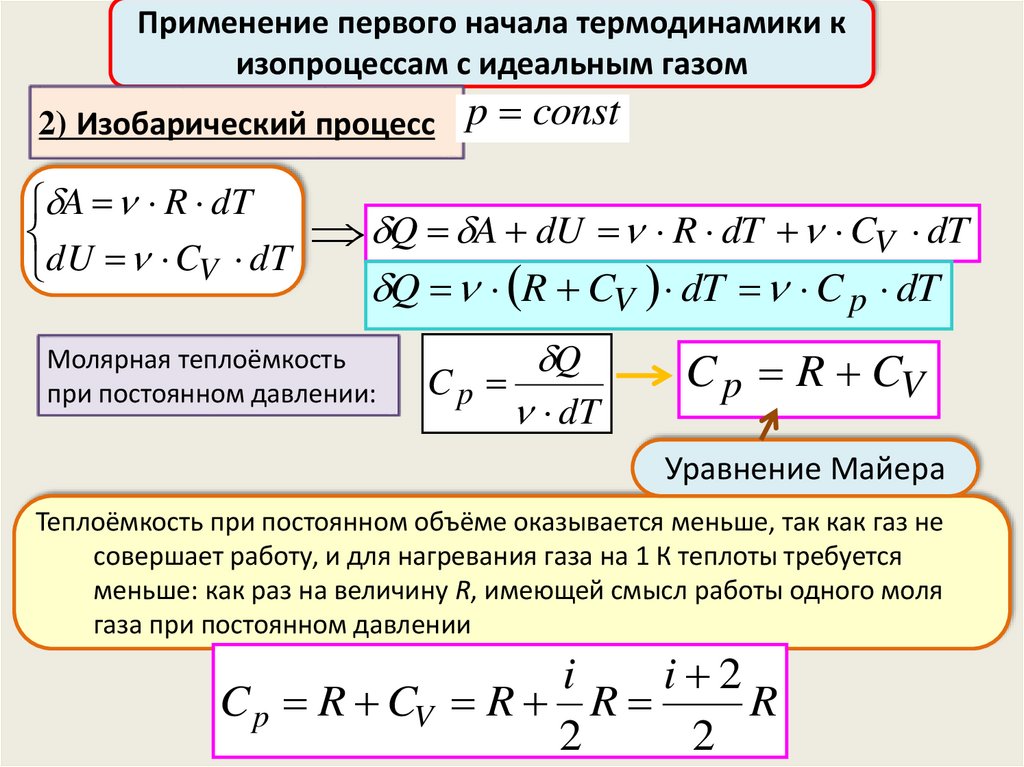
2) Изобарический процесс
p const
A R dT
Q A dU R dT CV dT
dU CV dT
Q R CV dT C p dT
Молярная теплоёмкость
при постоянном давлении:
Cp
Q
dT
C p R CV
Уравнение Майера
Теплоёмкость при постоянном объёме оказывается меньше, так как газ не
совершает работу, и для нагревания газа на 1 К теплоты требуется
меньше: как раз на величину R, имеющей смысл работы одного моля
газа при постоянном давлении
i
i 2
C p R CV R R
R
2
2
32.
Применение первого начала термодинамики кизопроцессам с идеальным газом
3) Изотермический процесс
dT 0
T const
dU CV dT 0 U 0
Q A dU A p dV
Q A
V2
Q12 A12 RT ln
V1
33.
4) Адиабатический процесспротекает без теплообмена с
окружающей средой:
система не получает и не отдаёт теплоты
Q 0
Q 0
Адиабатными процессами будут процессы, протекающие
1) в системе с хорошей теплоизоляцией;
2) очень быстрые процессы, – система не успевает обменяться
теплотой с окружающей средой за время протекания процесса
По первому началу термодинамики:
Q A dU 0
A dU
A U
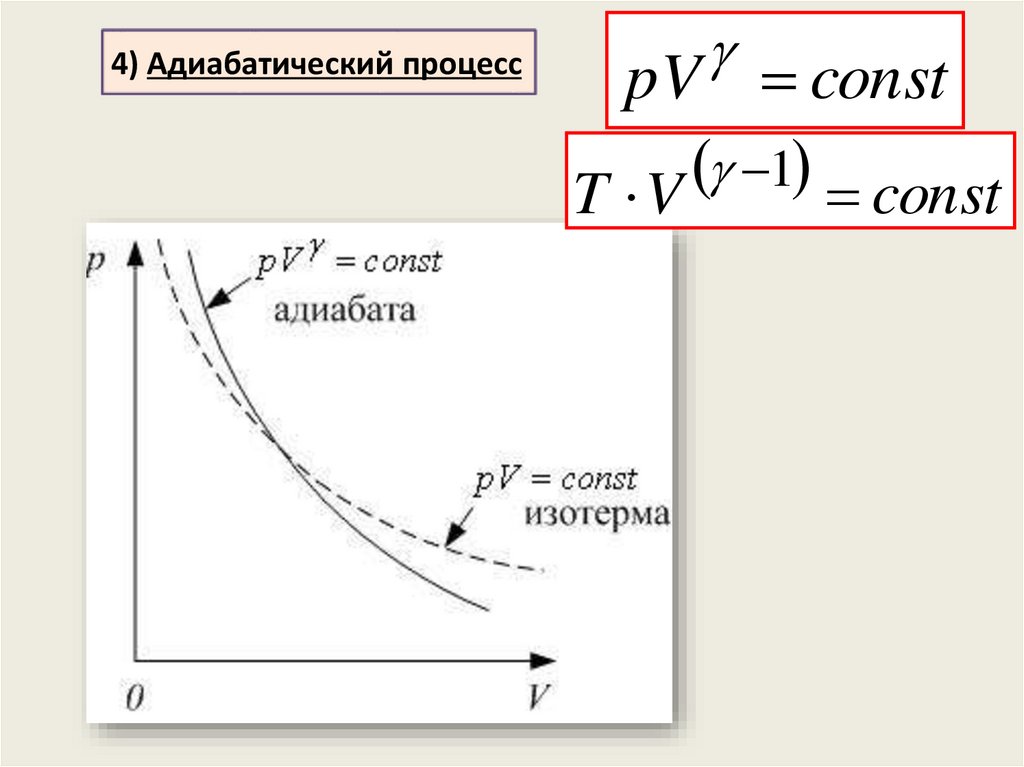
34.
4) Адиабатический процессpV const
1
T V
const
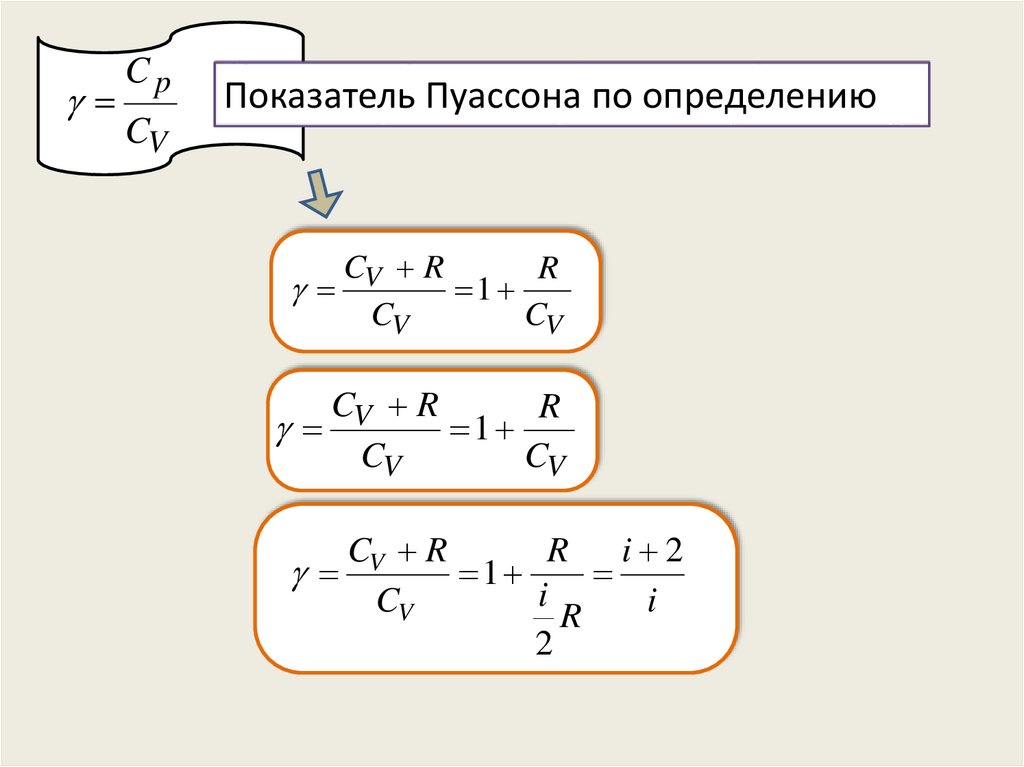
35.
CpCV
Показатель Пуассона по определению
CV R
R
1
CV
CV
CV R
R
1
CV
CV
CV R
R i 2
1
i
CV
i
R
2
36.
Работа в адиабатическом процессе1
T V
const
По первому началу термодинамики:
A12 U CV T2 T1
V1
T2 T1
V2
1
T2 V2 1 T1 V1 1
V 1
V 1
A12 CV T1 1 T1 CV T1 1 1
V2
V2
1
1
V1 p1V1 V1
R
A12
T1 1
1
1 V2 1 V2
37.
Круговой процесс (цикл)Цикл – замкнутый процесс, при котором система, пройдя ряд
последовательных состояний, возвращается в исходное состояние
Прямой
Тепловая машина совершает
механическую работу за счёт тепловой
энергии.
Непрерывно действующая тепловая
машина должна работать периодически
Обратный
Холодильная машина отводит
тепло от более холодного
тела к более нагретому;
при этом должна затрачиваться
некоторая работа
37
38.
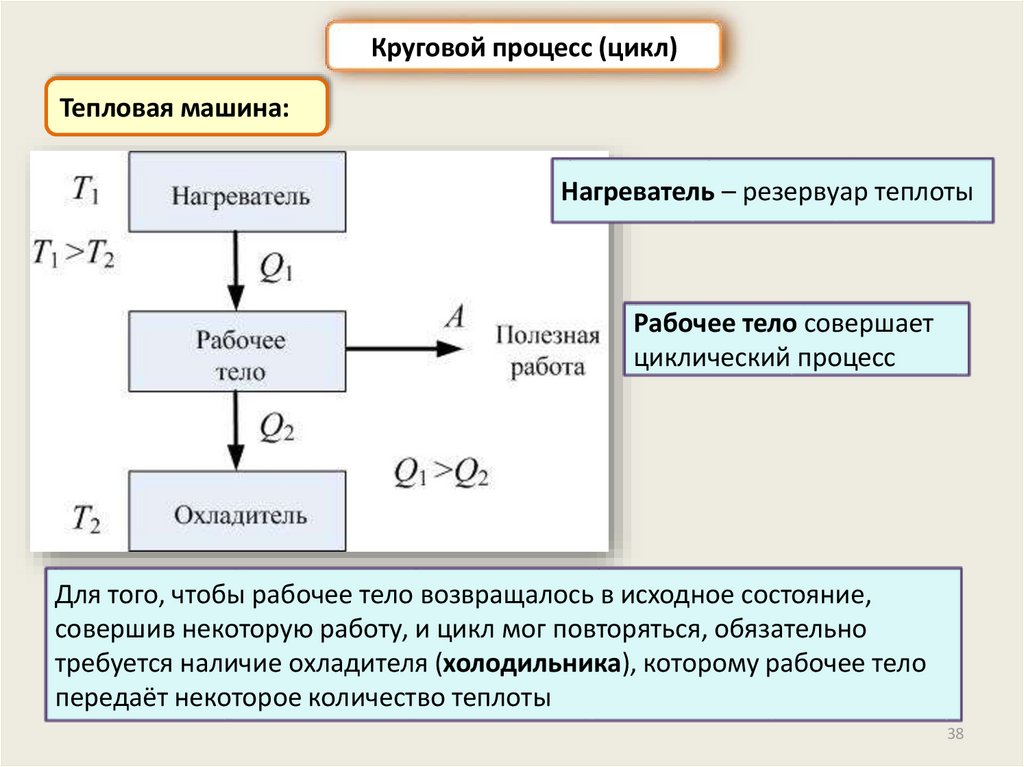
Круговой процесс (цикл)Тепловая машина:
Нагреватель – резервуар теплоты
Рабочее тело совершает
циклический процесс
Для того, чтобы рабочее тело возвращалось в исходное состояние,
совершив некоторую работу, и цикл мог повторяться, обязательно
требуется наличие охладителя (холодильника), которому рабочее тело
передаёт некоторое количество теплоты
38
39.
Круговой процесс (цикл)Тепловая машина:
Разобьём прямой цикл на два
процесса:
1) расширения от
минимального объёма
до максимального
2) сжатия (2→1).
По первому началу термодинамики:
Q1 A1 U12 A1 U 2 U1
Q2 A2 U 21 A2 U1 U 2
Количество теплоты,
полученное за весь цикл:
Q Q1 Q2
40.
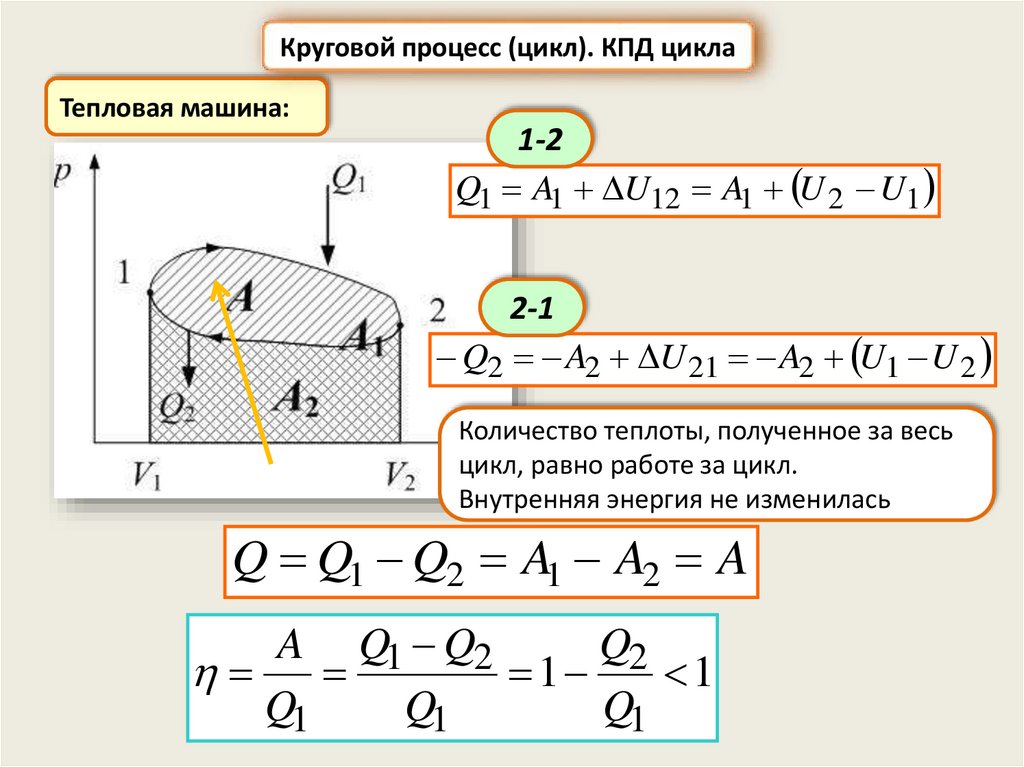
Круговой процесс (цикл). КПД циклаТепловая машина:
1-2
Q1 A1 U12 A1 U 2 U1
2-1
Q2 A2 U 21 A2 U1 U 2
Количество теплоты, полученное за весь
цикл, равно работе за цикл.
Внутренняя энергия не изменилась
Q Q1 Q2 A1 A2 A
A Q1 Q2
Q2
1
1
Q1
Q1
Q1
41.
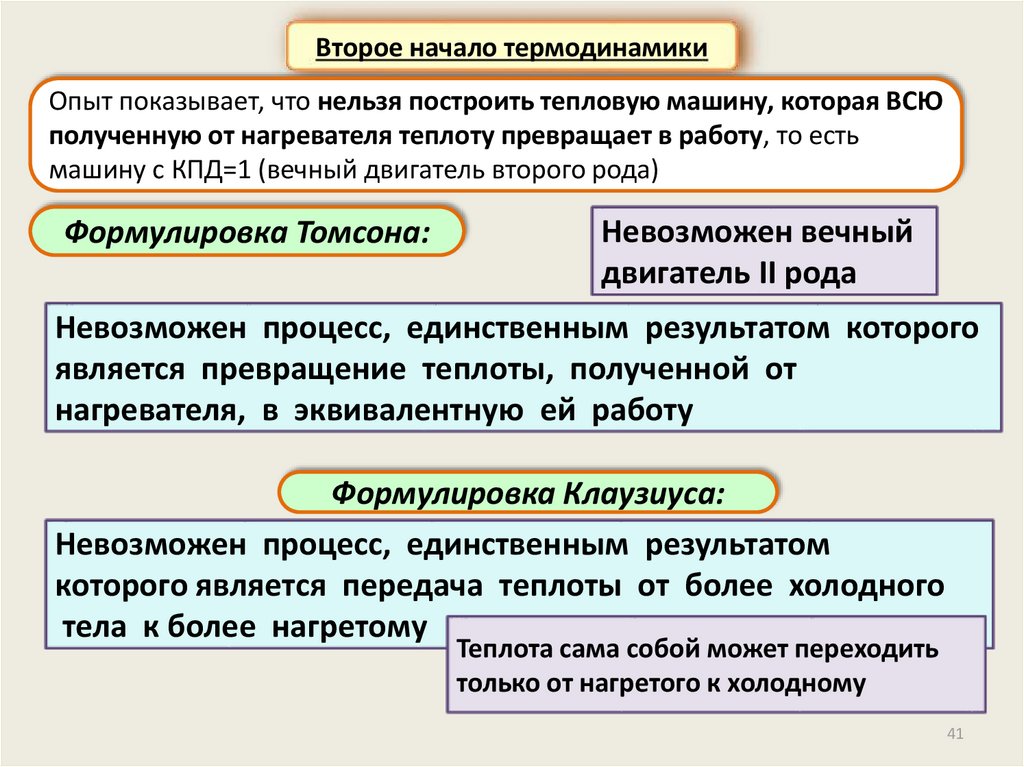
Второе начало термодинамикиОпыт показывает, что нельзя построить тепловую машину, которая ВСЮ
полученную от нагревателя теплоту превращает в работу, то есть
машину с КПД=1 (вечный двигатель второго рода)
Формулировка Томсона:
Невозможен вечный
двигатель II рода
Невозможен процесс, единственным результатом которого
является превращение теплоты, полученной от
нагревателя, в эквивалентную ей работу
Формулировка Клаузиуса:
Невозможен процесс, единственным результатом
которого является передача теплоты от более холодного
тела к более нагретому
Теплота сама собой может переходить
только от нагретого к холодному
41
42.
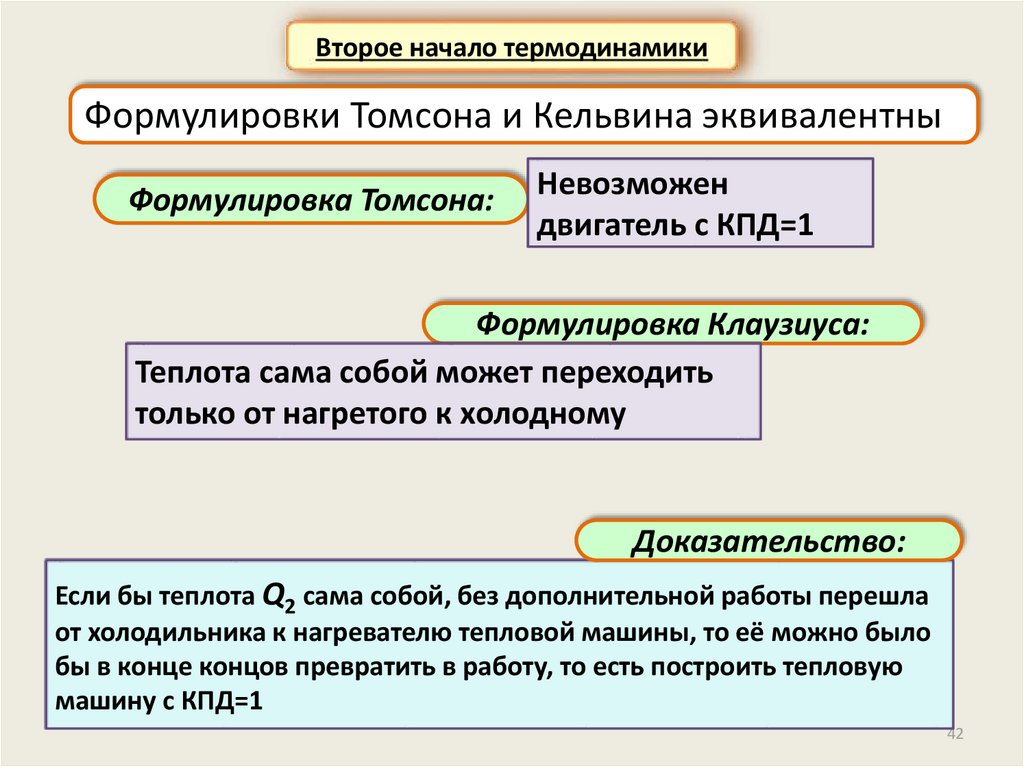
Второе начало термодинамикиФормулировки Томсона и Кельвина эквивалентны
Формулировка Томсона:
Невозможен
двигатель с КПД=1
Формулировка Клаузиуса:
Теплота сама собой может переходить
только от нагретого к холодному
Доказательство:
Если бы теплота Q2 сама собой, без дополнительной работы перешла
от холодильника к нагревателю тепловой машины, то её можно было
бы в конце концов превратить в работу, то есть построить тепловую
машину с КПД=1
42
43.
Обратимые и необратимые процессыТермодинамический процесс называется обратимым, если он может
проходить как в прямом, так и в обратном направлении; при этом после
возвращения системы в исходное состояние в окружающей среде и в
самой системе не происходит никаких изменений
Пример обратимого процесса:
абсолютно упругое соударение
Примеры необратимых процессов: неупругое соударение,
трение, диффузия, теплопроводность
Обратимые процессы – идеализация
Все реальные процессы в той или иной степени необратимы
Равновесный (квазистатический) процесс представляет собой
непрерывную последовательность равновесных состояний.
Любая точка такого процесса – состояние равновесия, из которого
система может идти как в прямом, так и в обратном направлении.
Отсюда следует, что любой равновесный процесс обратим.
Только равновесные процессы можно изображать графически
В обратимых процессах система совершает максимальную работу
КПД максимален
43
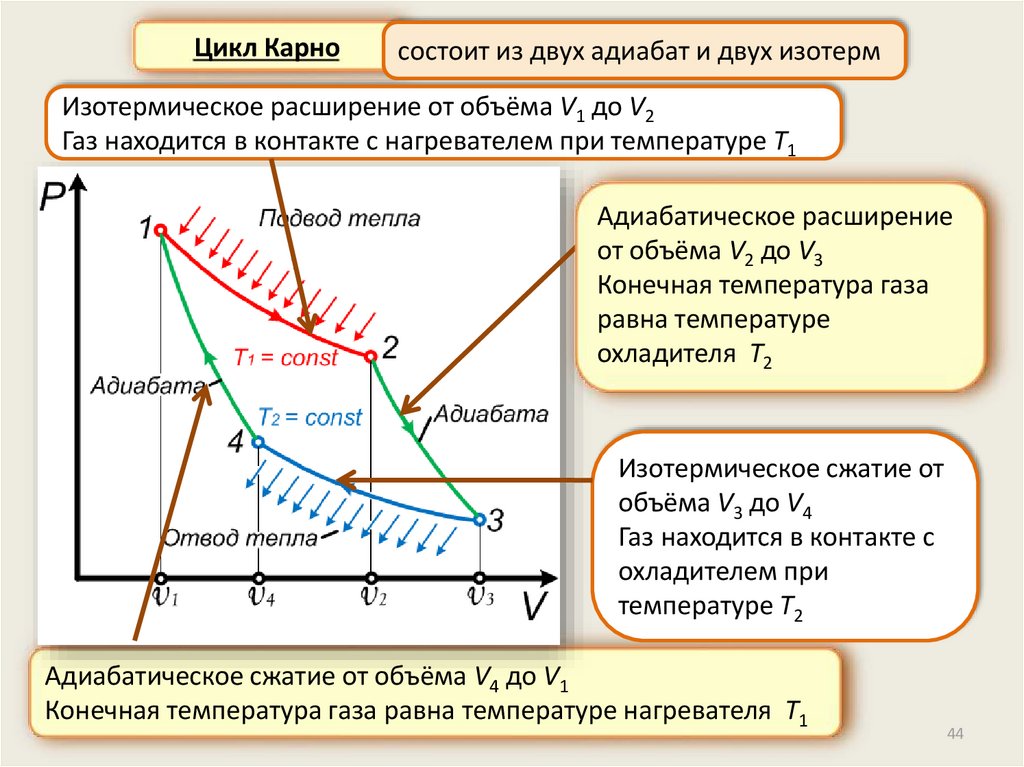
44.
Цикл Карносостоит из двух адиабат и двух изотерм
Изотермическое расширение от объёма V1 до V2
Газ находится в контакте с нагревателем при температуре T1
Адиабатическое расширение
от объёма V2 до V3
Конечная температура газа
равна температуре
охладителя T2
Изотермическое сжатие от
объёма V3 до V4
Газ находится в контакте с
охладителем при
температуре T2
Адиабатическое сжатие от объёма V4 до V1
Конечная температура газа равна температуре нагревателя T1
44
45.
Цикл Карно. КПД цикла КарноV2
Q1 A12 RT1 ln
V1
V3
Q2 A34 RT2 ln
V4
T1V1 1 T2V4 1
T1V2 1 T2V3 1
V2 V3
V1 V4
Q1 Q2
к
Q1
T1 T2
к
T1
к
V2
V
RT2 ln 3
V1
V4
V
RT1 ln 2
V1
RT1 ln
45
46.
Теорема Карно1) КПД цикла Карно не зависит от природы рабочего тела и
определяется только температурами нагревателя и
охладителя:
T T
к
1
2
T1
2) КПД любого обратимого цикла не больше КПД цикла
Карно с теми же температурами нагревателя и охладителя:
T1 T2
обр. К
T1
3) КПД любого необратимого цикла меньше КПД цикла
Карно с теми же температурами нагревателя и охладителя:
T1 T2
необр. К
T1 46





























 Физика
Физика








