Похожие презентации:
Аналитическая геометрия
1. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
ПЛОСКАЯЛИНИЯ И ЕЕ УРАВНЕНИЕ В R2
ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ. УРАВНЕНИЕ ПРЯМОЙ ПО
ТОЧКЕ И НОРМАЛЬНОМУ ВЕКТОРУ
УРАВНЕНИЕ ПРЯМОЙ ПО ТОЧКЕ И НАПРАВЛЯЮЩЕМУ
ВЕКТОРУ
УРАВНЕНИЕ ПРЯМОЙ ПО ДВУМ ТОЧКАМ
УРАВНЕНИЕ ПРЯМОЙ ПО ТОЧКЕ И УГЛОВОМУ
КОЭФФИЦИЕНТУ
УРАВНЕНИЕ ПРЯМОЙ С УГЛОВЫМ КОЭФФИЦИЕНТОМ.
УГОЛ МЕЖДУ ДВУМЯ ПРЯМЫМИ
2.
ОПРЕДЕЛЕНИЕ Уравнение F( x, y) 0 , связывающее между собой переменные x и y называютуравнением плоской линии в выбранной системе
координат, если координаты x и y любой точки M
этой линии ему удовлетворяют , а координаты всех точек , не лежащих на ней , ему не удовлетворяют .
3. ПРИМЕР
Построить линию, заданнуюуравнением
Придавая переменной
различные числовые
значения и вычисляя
соответствующие значения ,
построим таблицу
Введем на плоскости
декартову систему координат
и построим на этой плоскости
соответствующие точки с
координатами. Соединяя
построенные точки линией,
получим искомую кривую
y x
x
y
0
0
1
1
4
2
9
3
...
...
y
x
0
Рис. 1.1
4.
ОПРЕДЕЛЕНИЕ Уравнение F( x, y) 0 называется алгебраическим, еслиk
m
выражение F( x, y) есть сумма конечного числа слагаемых вида Ax y , где
k, m целые неотрицательные числа, A -действительное число. При этом
наибольшая из сумм степеней k m называется
степенью уравнения.
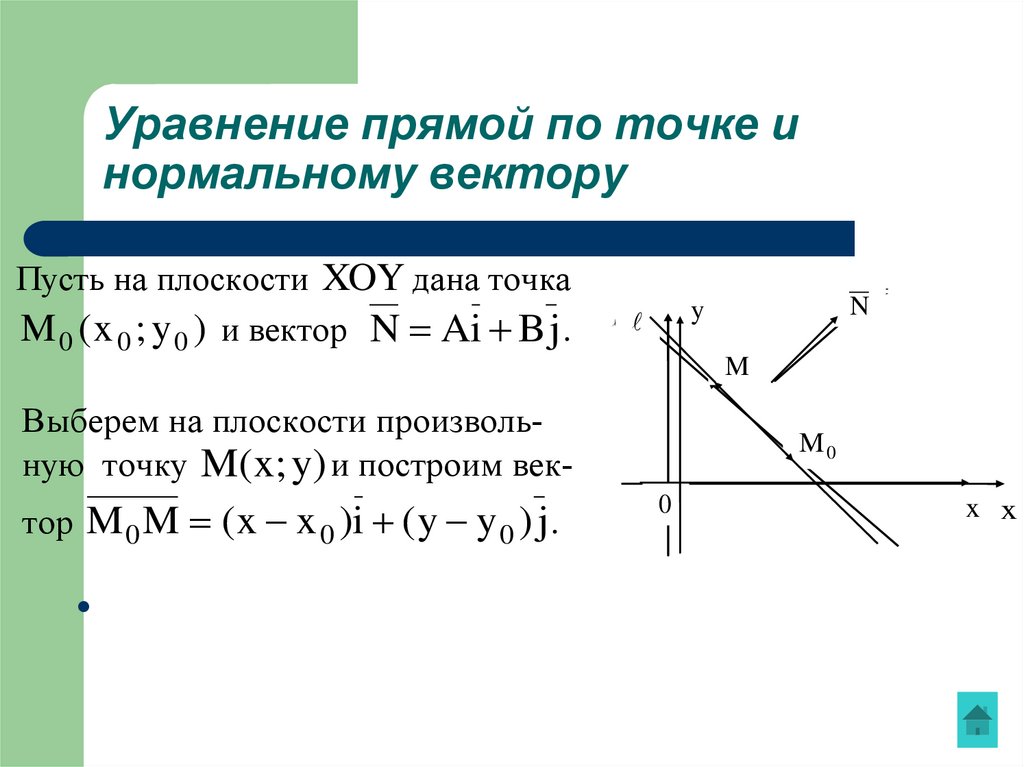
5. ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ. УРАВНЕНИЕ ПРЯМОЙ ПО ТОЧКЕ И НОРМАЛЬНОМУ ВЕКТОРУ
Положениепрямой на координатной плоскости
вполне определяется заданием
любых двух ее точек
точки и вектора, параллельного прямой
точки и вектора, перпендикулярного прямой
углового коэффициента и отрезка,
отсекаемого прямой от оси OY
других величин.
6. Уравнение прямой по точке и нормальному вектору
Пусть на плоскости XOY дана точкаM 0 ( x 0 ; y 0 ) и вектор N Ai B j .
M
M
Выберем на плоскости произвольную точку M( x; y) и построим вектор M 0 M ( x x 0 )i ( y y 0 ) j .
NN
yy
M
M0 0
00
x x
Рис. 1.3
Рис.
1.3
7. Рассмотрим два случая:
M 0 M N M 0 M N 0 илиA( x x 0 ) B( y y 0 ) 0 ;
1) пусть точка M .Тогда
2) если точка M , то векторы M 0 M и N не перпендикулярны. Следовательно M 0 M N 0 или A( x x 0 ) B( y y 0 ) 0 .
Таким образом, в п. 1 получено уравнение искомой прямой .
Уравнение п.1. называется уравнением прямой по точке и нормально-
му вектору N A; B .
8. УРАВНЕНИЕ ПРЯМОЙ ПО ТОЧКЕ И НАПРАВЛЯЮЩЕМУ ВЕКТОРУ
Пусть на плоскости XOY дана точка M 0 ( x 0 ; y 0 ) и вектор S mi n j.y
M
Требуется определить уравнение прямой проходящей через точку M 0 ( x 0 ; y 0 ) параллельно
вектору S (вектор S называется направляющим
вектором прямой).
S
M0
x
0
Рис. 1.4
Выберем
на
плоскости
XOY произвольную точку
M(x; y) и построим вектор M 0 M ( x x 0 )i ( y y 0 ) j .
9. Рассмотрим два случая:
1) пусть точка M .Тогда M 0 M S . Следовательно, векторыM 0 M и S коллинеарны. Итак, M 0 M S , где - некоторое
( x x 0 )i ( y y 0 ) j (mi n j)
x x 0 y y0
x x 0 y y0
x x 0 m
;
m
n
m
n
y y 0 n
2) пусть точка M .Тогда M 0 M S при любом . Отсюда и
x x 0 y y0
. Из 1) и 2) и определения уравнения линии следует, что
m
n
уравнение п.1 является уравнением искомой прямой . Это уравнение называется уравнением прямой по точке и направляющему вектору S m; n .
действительное число. Тогда
Его также называют каноническим уравнением прямой.
10. Замечание
Если прямая проходит через точку M 0 ( x 0 ; y 0 ) и параллельна оси OX ,то направляющий вектор S также параллелен этой оси. Следовательно,
S m;0 . Хотя его проекция n 0 , уравнение этой прямой условились
x x 0 y y0
записывать в канонической форме, т.е. в форме
. Последнее
m
0
уравнение считается другой формой записи уравнения этой прямой y y 0 .
x x 0 y y0
Аналогично каноническое уравнение вида
означает дру0
n
гую форму записи уравнения прямой x x 0 , проходящей через точку
M 0 ( x 0 ; y 0 ) параллельно оси OY .
11.
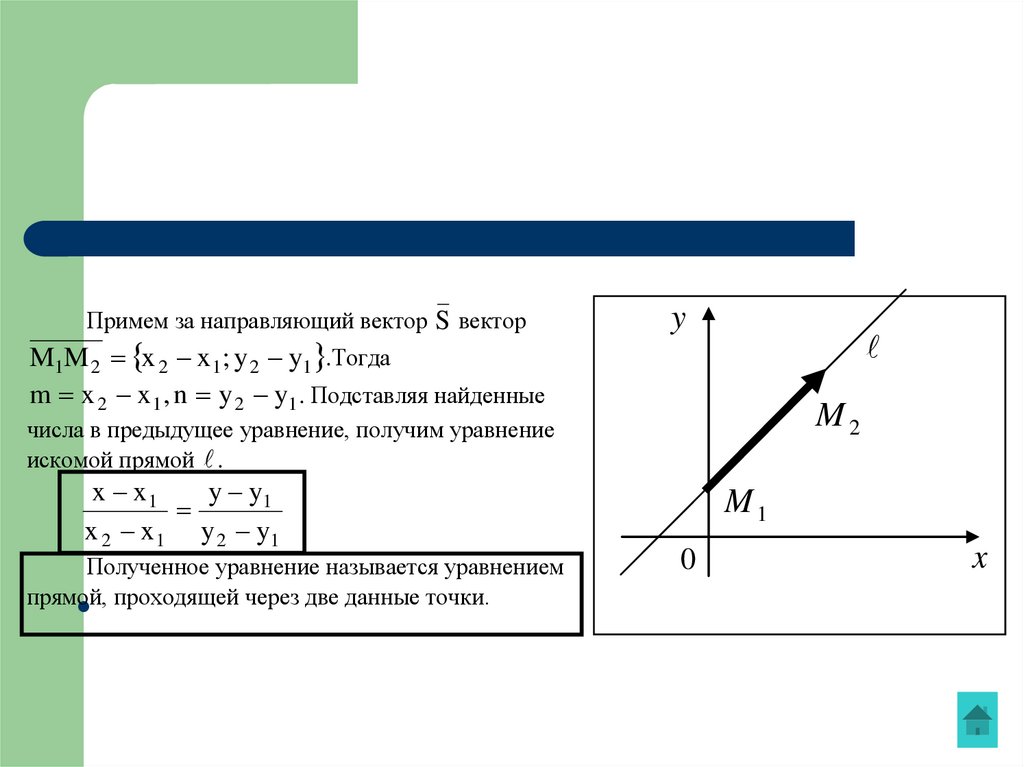
Примем за направляющий вектор S векторM1M 2 x 2 x1 ; y 2 y1 .Тогда
m x 2 x1 , n y 2 y1 . Подставляя найденные
y
M2
числа в предыдущее уравнение, получим уравнение
искомой прямой .
x x1
y y1
x 2 x 1 y 2 y1
Полученное уравнение называется уравнением
прямой,
проходящей через две данные точки.
M1
x
0
Рис. 1.5
12. УРАВНЕНИЕ ПРЯМОЙ ПО ТОЧКЕ И УГЛОВОМУ КОЭФФИЦИЕНТУ
yПусть на плоскости XOY проведена некоторая прямая .
Углом наклона прямой к оси OX называется угол, на который нужно повернуть вокруг начала координат против
движения часовой стрелки ось абсцисс 0
так, чтобы она стала параллельна данной
прямой.
x
Рис.1.6
13.
Тангенс угла наклона прямой называется угловым коэффициентом прямой и обозначается буквой k . Итак,k tg
Заметим, что если острый угол, то k 0 , если тупой,
то k 0 , если 0 , то k 0 , если , то k не суще2
ствует.
14.
y0
S0
M0
Рис.1.7
x
15.
0Так как cos cos sin , то S cos ; sin .
2
Полагая m cos , n sin , получим
x x 0 y y0
sin
y y0
(x x 0 )
cos
sin
cos
y y 0 tg ( x x 0 ) y y 0 k ( x x 0 )
Полученное уравнение называется уравнением прямой по точке и угловому
коэффициенту.
16.
Пусть требуется найти уравнение прямой , если проходит черезточку M 0 ( x 0 ; y 0 ) и имеет угловой коэффициент k . Как известно, уравнение любой прямой проходящей через точку M 0 ( x 0 ; y 0 ) запишется в виде
x x 0 y y0
,
m
n
где m и n есть координаты направляющего вектора S . В качестве направляющего вектора прямой примем единичный вектор S cos ; cos ,
составляющий с осью OX тот же угол , что и прямая .
0














 Математика
Математика








