Свойства логарифмов

1.

•Тема урока:
• « СВОЙСТВА ЛОГАРИФМОВ»
Задачи: повторить теоретический
материал.
5klass.net

2.

Определение логарифма
Логарифмом положительного числа b
по основанию а, где а больше 0 и а≠ 1
называется показатель степени,
в которую нужно возвести а, чтобы
получить b.
log a b c ,
a 0,
a b,
a 1,
c
b 0

3.

Основное логарифмическое
тождество
a
loga b
b, где a 0, a 1, b 0

4.

История возникновения
логарифмов
Слово логарифм происходит из двух
греческих слов и оно переводится, как
отношение чисел.
В течение ХVI в. резко возрос объем работы,
связанный с проведением приближенных
вычислений в ходе решения разных задач, и в
первую очередь задач астрономии, имеющей
непосредственное практическое применение
(при определения положения судов по звездам и
по Солнцу).

5.

Логарифмы необычайно быстро вошли в практику.
Изобретатели логарифмов не ограничились
разработкой новой теории. Было создано
практическое средство – таблицы логарифмов, резко повысившее производительность труда
вычислителей. Добавим, что уже в 1623 г., т.е. всего
через 9 лет после издания первых таблиц,
английским математиком Д. Гантером была
изобретена первая логарифмическая линейка,
ставшая рабочим инструментом для многих
поколений.
Первые таблицы логарифмов составлены
независимо друг от друга шотландским
математиком Дж. Непером (1550 - 1617) и
швейцарцем И. Бюрги (1552 - 1632). В
таблицы Непера вошли значения логарифмов
синусов, косинусов и тангенсов для углов от
0 до 900 с шагом в 1 минуту. Бюрги
подготовил свои таблицы логарифмов чисел,
но вышли в свет они в 1620 г., уже после
издания таблиц Непера, и поэтому остались
незамечеными.
Непер Джон ( 1550-1617 )

6.

Поэтому открытие
логарифмов, сводящее
умножение и деление чисел
к сложению и вычитанию
их логарифмов, удлинило по
выражению Лапласа, жизнь
вычислителей.
Изобретение
логарифмов,
сократив
работу астронома,
продлила ему жизнь.
П. С. Лаплас

7.

Свойства степени
m
а аn
п m
1
а п
а
п

8.

1. Логарифм произведения равен сумме
логарифмов множителей:
log x ab log x a log x b
2. Логарифм частного равен логарифмов
делимого без логарифма делителя:
a
log x log x a log x b
b

9.

3. Логарифм степени равен
произведению показателя степени на
логарифм ее основания:
log x a m log x a
m
4. Основание логарифма в степени
log a к
1
x log а х
к

10.

5. Основное логарифмическое
тождество
а
logа х
х
6. Переход от одного основания к другому
log b x
1
log a x
log a x
log b a
log x a

11.

Частные свойства:
1)log a 1 = 0;
2) log a a = 1;
3) log a (1/a) = - 1;
4) log a a m = m;
5) log a m a = 1/m.

12.

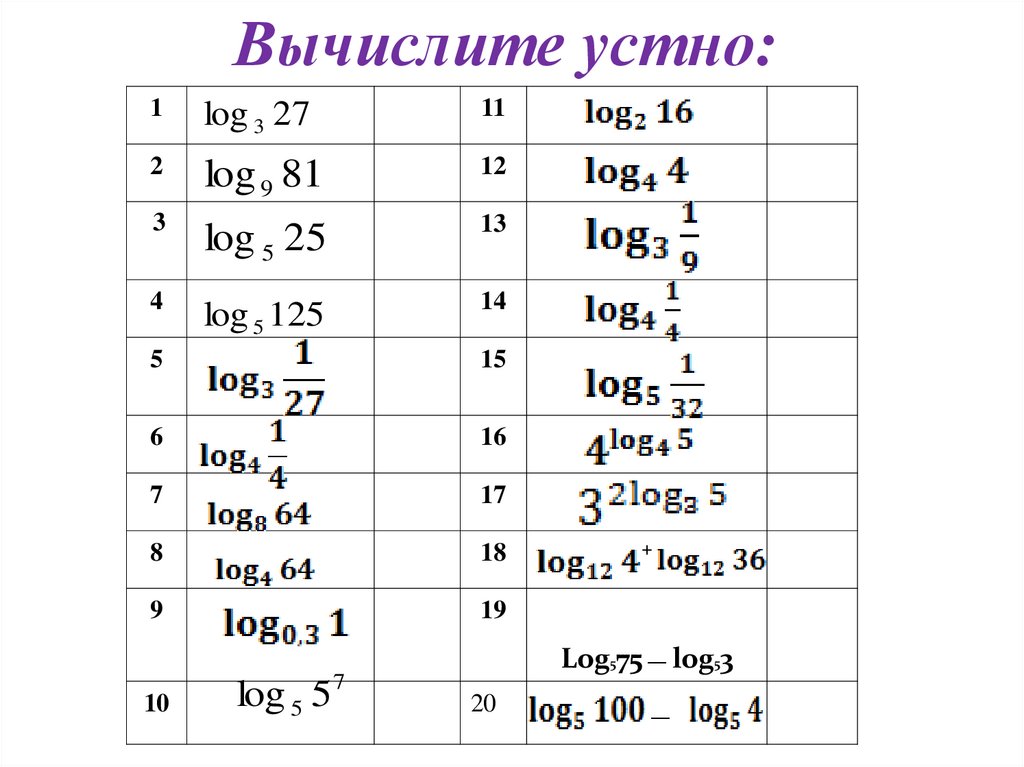
Вычислите устно:
1
log 3 27
11
2
log 9 81
12
3
log 5 25
13
4
log 5 125
14
5
15
6
16
7
17
8
18
9
19
10
log 5 5
7
+
Log575 ― log53
20
―

13.

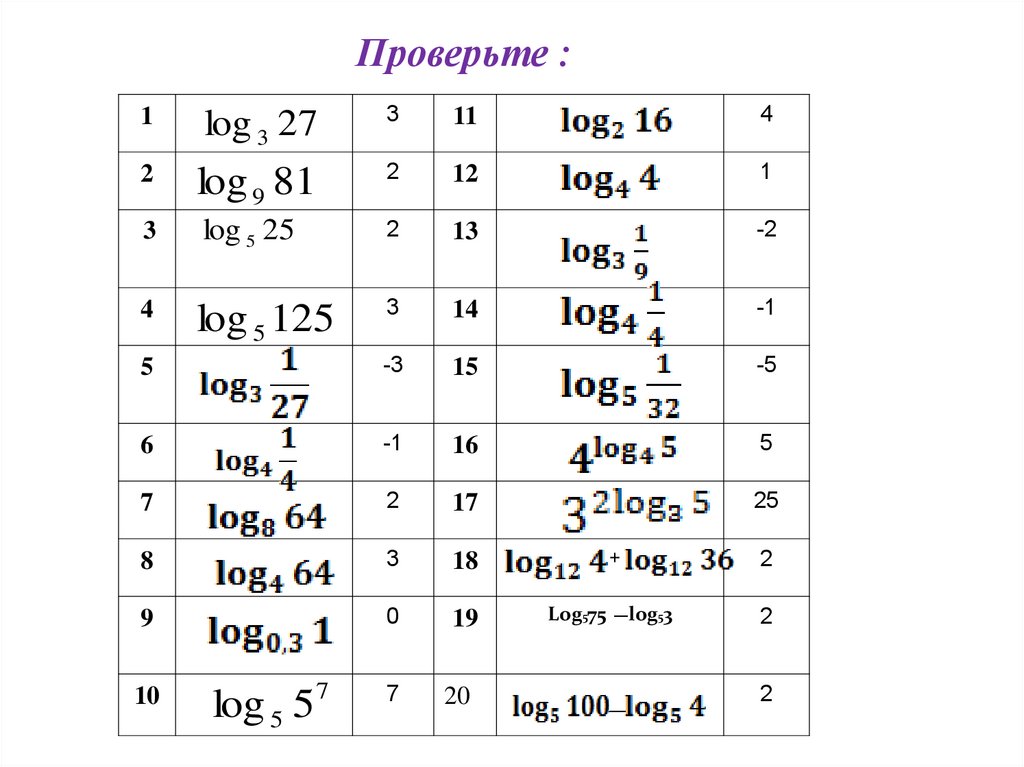
Проверьте :
1
log 3 27
3
11
4
2
log 9 81
2
12
1
3
log 5 25
2
13
-2
4
log 5 125
3
14
-1
5
-3
15
-5
6
-1
16
5
7
2
17
25
8
3
18
9
0
19
10
log 5 57
7
20
Log575
+
2
―log53
2
―
2

14.

Найдите вторую половину формулы
(устно)
+
-
-
1
0

15.

Проверьте :
+
1
0