Линейная алгебра. Прямая в пространстве. (Часть 12)

1.

Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Оренбургский государственный университет»
Кафедра прикладной математики
И.Г. Руцкова
Электронный курс лекций «Линейная алгебра»,
часть 12
Оренбург 2016

2.

M x; y ; z l
M 0 M x x0 ; y y0 ; z z0 l
x x0 y y0 z z0
m
n
p
M 0 M || s
M 0 M t s ,t R;
t R ; x x0 mt , t R
y y0 nt ,
z z pt ,
0
x x0 tm ,
y y0 tn ,
z z tp ,
0
r OM ,
r0 OM 0 ,
r r0 t s ,t R
M 0 M r r0 ;
r r0 , s 0

3.

Пример 1.
Решение.
x 2 y 5 z 7
4
6
9
x 2 4t ,
y 5 6t ,
z 7 9t ,
t R.
Пример 2.
Решение.
s 5;6;1 ;
x 1 y 6 z 5
5
6
1
Пример 3.
Решение.
s k 0;0;1 ,
x 1 0 t ,
y 6 0 t,
z 5 1 t ,
t R.

4.

M 0 x0 ; y0 ; z0 M1 x1 ; y1 ; z1 , s M1M 2 x2 x1 ; y2 y1 ; z2 z1
x x1
y y1
z z1
,
x2 x1 y2 y1 z2 z1
x x1 x2 x1 t ,
y y1 y2 y1 t ,
z z z z t ,
1
2
1
r r1 t r2 r1 ,t R ,
Пример 4.
M1 3;5;4 ,
M 2 1;10;15
x 3
y 5 z 4
,
1 3 10 5 15 4
x 3 y 5 z 4
;
4
5
11
t R
r r1 ,r2 r1 0 ,
x 3 1 3 t ,
y 5 10 5 t ,
z 4 15 4 t ,
x 3 4t ,
y 5 5t ,
z 4 11t ,
t R

5.

Пример 5.
ешение.
xD
xA xB 3 5
y yB 6 2
z z
7 3
1, yD A
4, z D A B
2
2В
2
2
2
2
2
M1 C , M 2 D
D
С
А
x 4 1 4 t ,
y 7 4 7 t ,
z 2 2 2 t ,t R;
x 4 5t ,
y 7 11t ,
z 2,t R;
Пример 6.
x 6 12 6 t ,
l : y 6 6 6 t ,
z 5 1 5 t ,t R;
x 6 18t ,
y 6 12t ,
z 5 6t ,t R;
5
P1 l XOY : z 0 5 6t 0 t , P1 9; 4;0 ;
6
Решение.
Z
Y
X
1
P 2 l XOZ : y 0 6 12t 0 t ,
2
1
P 3 l YOZ : x 0 6 18t 0 t ,
3
P2 3;0; 2 ;
P3 0;2; 3

6.

Общее уравнение прямой в пространстве
A1 x B1 y C1 z D1 0,
A2 x B2 y C2 z D2 0,
s n1 ,n2 ,
Пример 3.
i
s 1
3
n1 A1 , B1 ,C1 ,
n2 A2 , B2 ,C2
x 2 y 3z 4 0,
3x 2 y 5z 4 0,
j
k
2
3 1 3 1 2
2 3 i
j
k
4 i 14 j 8 k
2 5
3 5
3 2
2 5
x 2 y 3z 4,
3x 2 y 5z 4;
3 4
1 2
1 2 3 4
~
3 2 5 4
0 8 14 8
x 2 y 4 3z ,
x 2 y 3z 4,
8 y 14 z 8, 8 y 8 14 z .
z 0,
x 2 y 1 z 0
4
14
8
2 способ.
z 8,
y 1,
y 13,
x 2
x 6
M1 2; 1;0 ;
M 2 6;13;8

7.

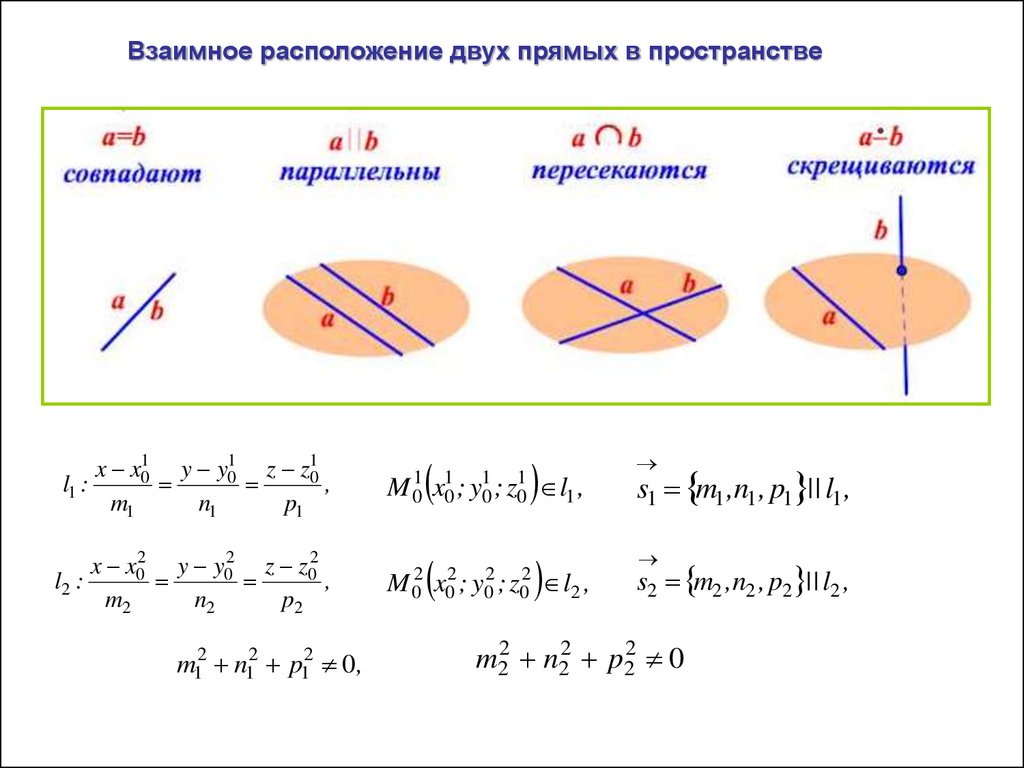
Взаимное расположение двух прямых в пространстве
x x10 y y10 z z10
l1 :
,
m1
n1
p1
M 01
x10 ; y10 ; z10
l ,
x x02 y y02 z z02
l2 :
,
m2
n2
p2
M 02
l ,
m12 n12 p12 0,
x02 ; y02 ; z02
1
2
s1 m1 ,n1 , p1 || l1 ,
s2 m2 ,n2 , p2 || l2 ,
m22 n22 p22 0

8.

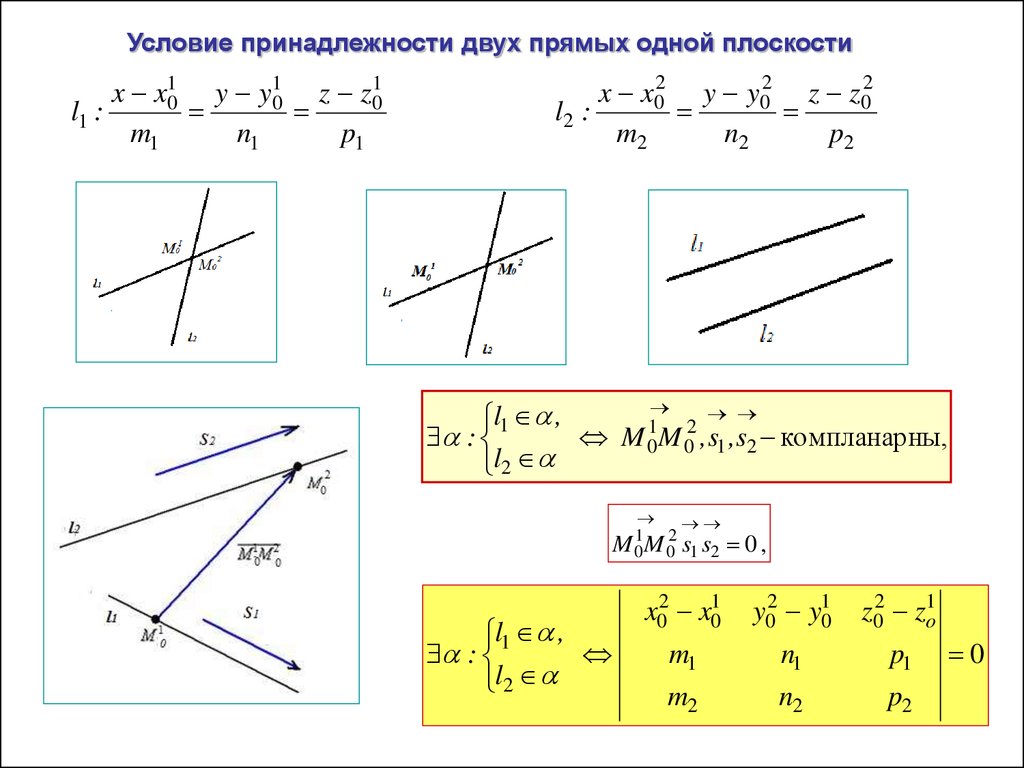
Условие принадлежности двух прямых одной плоскости
x x10 y y10 z z10
l1 :
m1
n1
p1
x x02 y y02 z z02
l2 :
m2
n2
p2
l1 ,
1 2
:
M 0 M 0 , s1 , s2 компланарны,
l2
1 2
M 0 M 0 s1 s2
l1 ,
:
l2
x02 x10
m1
m2
0,
y02 y10
n1
n2
z02 z1o
p1 0
p2

9.

Пример 4
Решение.
M 01
l1 :
x 3 y 2 z 6
,
2
3
4
3; 2;6 , s1 2;3; 4 ,
x02 x10
m1
m2
y02 y10
n1
n2
M 02
l2 :
x 5 y 1 z 4
1
4
1
5; 1; 4 , s2 1; 4;1 ,
1 2
M 0M 0
8;1; 10
z02 z1o 8 1 10
p1 2 3
4 24 80 4 30 2 128 134 134 0
p2
1 4 1
данные прямые принадлежат одной плоскости.
s1 и s2 - неколлинеарные, прямые пересекаются.

10.

Угол между прямыми в пространстве
x x10 y y10 z z10
l1 :
,
m1
n1
p1
l1 || l2
l1 l2
s1 || s2
s1 s2
x x02 y y02 z z02
l2 :
,
m2
n2
p2
m1 n1 p1
m2 n 2 p 2
n1 ,n2 0 m1m2 n1n2 p1 p2 0
а ) cos cos ,
б ) cos cos ,
cos cos
s1 , s2
| s1 | | s2 |
.

11.

Пример 9
Решение.
s1
s1 1; 1; 2 ; s2 1;1; 2 ; s1 , s2 1 1 1 1 2 2 2;
2
2
1
2
2
2
2
2
s2 1 1 2 2; cos
1 1 2 2;
; .
6
2 2 2
Пример 10

12.

Взаимное расположение прямой и плоскости в пространстве
l:
x x0 y y0 z z0
, m2 n 2 p 2 0;
m
n
p
: Ax By Cz D 0,
l
M 0 x0 , y0 , z0 l , s m,n, p || l ;
A B C 0;
2
2
2
n A; B;C
l || и l
M 0 x0 ; y0 ; z0 ,
s n ,
M 0 x0 ; y0 ; z0 ,
s n ,
Ax0 By0 Cz0 D 0,
mA nB pC 0.
Ax0 By0 Cz0 D 0 ,
mA nB pC 0.
mA nB pC 0
l
m n p
A B C
s || n

13.

Определение угла между прямой и плоскостью
sin
s , n
| s | | n |
0
2
Пример 1
Решение.
s 1;2;1 ; n 4;2; 2 ; s , n 1 4 2 2 1 2 6;
|6|
1
2
2
2
2
2
2
sin
;
| s | 1 2 1 6 ; | n | 4 2 2 24 2 6 ;
6
6 2 6 2
l
s || n
m n p
A B C
Пример 2
Решение.
s n 3; 2;5 ;
x 2 y 3 z 4
3
2
5

14.

Определение координат точки пересечения прямой и плоскости
x x0 mt ,
l : y y0 nt ,
z z pt ,
0
t R
: Ax By Cz D 0, A2 B2 C 2 0;
A x0 mt B y0 nt C z 0 pt D 0 ,
Ax0 Amt By0 Bnt Cz0 Cpt D 0 ,
Ax0 By0 Cz0 D t mA nB pC 0 ,
Ax0 By0 Cz0 D
t
tM ,
mA nB pC
xM x0 mtM ,
yM y0 ntM ,
z z pt .
0
M
M