Похожие презентации:
Математика. Управление социальными системами. Линейная алгебра. Матрицы
1.
МатематикаУправление
социальными системами
Линейная алгебра.
Матрицы
2.
МАТРИЦЫОПРЕДЕЛЕНИЯ
Матрицей размерности m x n называется прямоугольная таблица
чисел:
a11 a1n
A
a
a
mn
m1
содержащая m-строк и n-столбцов.
Числа aij ─ элементы матрицы (i-номер строки матрицы, j - номер
столбца матрицы, в которых расположен данный элемент)
3.
МАТРИЦЫОПРЕДЕЛЕНИЯ
Матрицу обозначают:
А
или
a
ij i 1, m
j 1, n
.
Матрица любой размерности называется нулевой (обозначают: О),
если все ее элементы равны нулю.
4.
МАТРИЦЫВиды матриц
Матрица размерности 1 x n называется матрицей-строкой:
(a11 … a1n).
Матрица размерности m x 1 называется матрицей-столбцом:
a11
a
m1
Если m=n , то матрица называется квадратной матрицей порядка n.
Ее элементы a11,…,ann образуют главную диагональ; их сумма
называется следом матрицы SpA; числа an1,an-1,2,…,a1n - побочную
диагональ.
5.
МАТРИЦЫВиды матриц
Квадратная матрица называется
верхнетреугольной
(нижнетреугольной), если все
ее элементы, расположенные
ниже (выше) главной диагонали,
равны нулю.
Квадратная матрица называется
диагональной, если все
элементы, стоящие вне главной
диагонали, равны нулю.
6.
МАТРИЦЫВиды матриц
Квадратная матрица называется единичной (обозначают: Е), если
она диагональная и все элементы главной диагонали равны единице.
7.
МАТРИЦЫВиды матриц
Матрица, полученная из квадратной матрицы А заменой всех строк
соответствующими (по номеру) столбцами, называется
транспонированной к матрице А и обозначается АT
Пример.
8.
МАТРИЦЫОПЕРАЦИИ НАД МАТРИЦАМИ
Две матрицы одинаковой размерности называются равными, если они
совпадают поэлементно.
1) Линейные операции
Суммой (разностью) матриц А и В размерности m x n называется
такая матрица А В
размерности m x n , у которой все элементы
равны сумме (разности) соответствующих элементов матриц А и В
9.
МАТРИЦЫОПЕРАЦИИ НАД МАТРИЦАМИ
Произведением матрицы А размерности m x n на число α
называется такая матрица α А размерности m x n , у
которой все элементы равны произведению
соответствующего элемента матрицы А на число α.
Операции умножения на число и сложения называются линейными
операциями.
10.
МАТРИЦЫОПЕРАЦИИ НАД МАТРИЦАМИ
Примеры.
11.
МАТРИЦЫОПЕРАЦИИ НАД МАТРИЦАМИ
П р и м е ры. Вычислить матрицу 2А 3В, если
0 1 2
,
А
1 7 3
4 3 1
.
В
0 5 6
Р е ш е н и е. Зная матрицы А и В, находим:
2 4
0
12 9
;
2 А
3В
2 14 6
0 15
0 12 2 9 4 3 12
2 А 3В
2 0 14 15 6 18 2
3
.
18
7 7
.
1 12
12.
МАТРИЦЫОПЕРАЦИИ НАД МАТРИЦАМИ
Свойства линейных операций
A B B A,
A A ,
A B C A B C ,
A A,
A B A B,
A A A,
где , const ;
A, B , C матрицы одинаковой размерности.
13.
МАТРИЦЫОПЕРАЦИИ НАД МАТРИЦАМИ
2) Умножение матриц
Произведением матрицы A a ij i 1, m размерности m x κ на матрицу B bij i 1, k
j 1, k
j 1, n
размерности κ x n называется такая матрица С размерности m x n , у
которой элемент с номером ij вычисляется по формуле:
c ij a i1 b1 j a i 2 b 2 j ... a ik b kj
(1)
Число (1) равно скалярному произведению вектора, составленного из
элементов i - й строки матрицы А, на вектор, составленный из элементов j го столбца матрицы В.
14.
МАТРИЦЫОПЕРАЦИИ НАД МАТРИЦАМИ
Пример.
15.
МАТРИЦЫОПЕРАЦИИ НАД МАТРИЦАМИ
Пример.
Следовательно,
коммутативности.
, т.е. умножение матриц не обладает свойством
16.
МАТРИЦЫОПЕРАЦИИ НАД МАТРИЦАМИ
Свойства операции умножения матриц:
A n m O m k O n k ,
O k n A n m O k m ,
A Е Е A A (для квадратных матриц),
A B C A B C ,
A B C A B A C ,
A B C A C B C.
Предполагается, что указанные здесь действия определены.
17.
МАТРИЦЫОПЕРАЦИИ НАД МАТРИЦАМИ
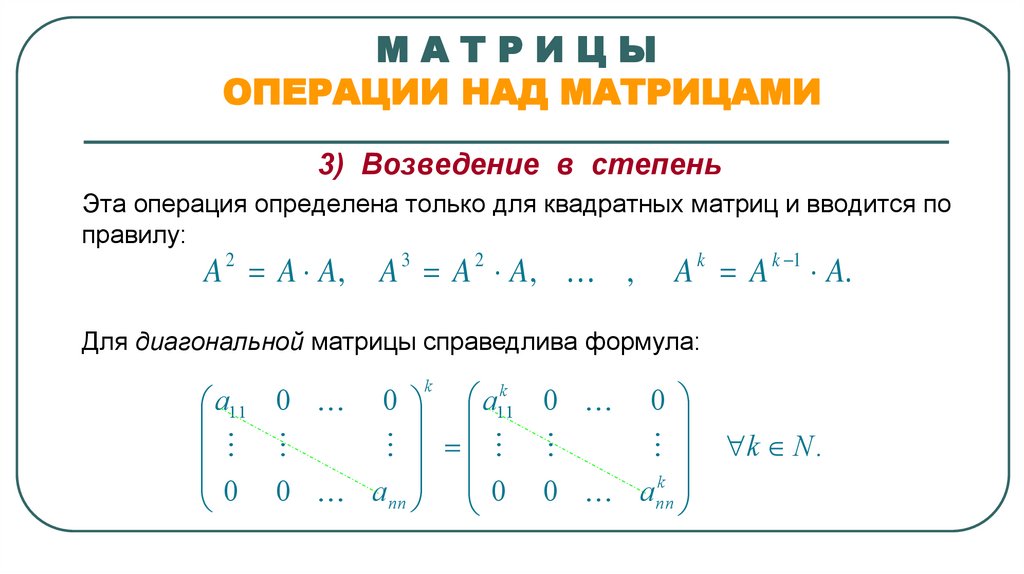
3) Возведение в степень
Эта операция определена только для квадратных матриц и вводится по
правилу:
A A A, A A A, ,
2
3
2
A A
k
k 1
A.
Для диагональной матрицы справедлива формула:
k
k
a11 0 0 a11 0 0
0 0 a 0 0 ak
nn
nn
k N .
18.
МАТРИЦЫОПЕРАЦИИ НАД МАТРИЦАМИ
П р и м е ры. Найти А2, если
1 0 1
А 3 2 1 ;
0 1 1
19.
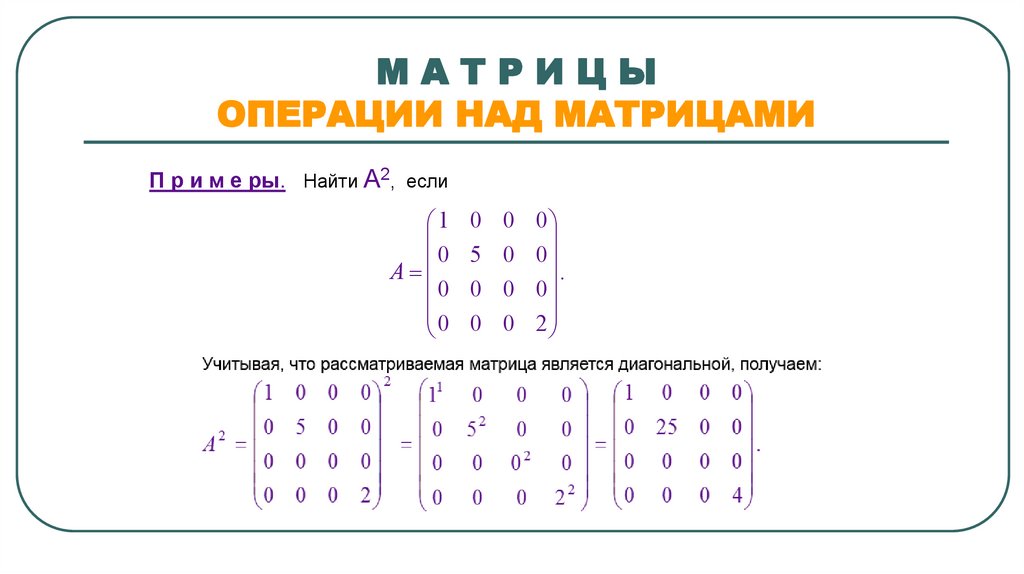
МАТРИЦЫОПЕРАЦИИ НАД МАТРИЦАМИ
П р и м е ры. Найти А2, если
1
0
А
0
0
0
5
0
0
0
0
0
0
0
0
.
0
2
20.
МАТРИЦЫЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ
О п р е д е л е н и е. Элементарными
преобразованиями строк матрицы называются
преобразования следующих типов:
1)
перестановка местами двух строк матрицы,
условное обозначение:
где стрелки указывают на строки, переставляемые
местами;
21.
МАТРИЦЫЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ
2) замена строки суммой этой строки и некоторой
другой, вспомогательной, предварительно умноженной
на какое-либо число α
условное обозначение: (α), где стрелка указывает
на изменяемую строку;
Множитель (α) ставят рядом со вспомогательной строкой;
22.
МАТРИЦЫЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ
3) умножение строки на ненулевое число α, условное
обозначение: (α), ставится рядом с изменяемой строкой .
З а м е ч а н и е 3. Аналогично вводятся элементарные
преобразования столбцов матрицы.
О п р е д е л е н и е. Опорным элементом строки матрицы
называется первый слева ненулевой элемент этой строки. Если
строка нулевая, то опорного элемента у нее нет.
23.
МАТРИЦЫСТУПЕНЧАТЫЙ ВИД МАТРИЦЫ
О п р е д е л е н и е. Матрица называется
ступенчатой (или имеющей
ступенчатый вид), если выполнены
следующие условия:
● если какая-то строка матрицы нулевая,
то все последующие строки нулевые;
● опорный элемент в каждой
последующей строке расположен
правее, чем в предыдущей.
Пример.
24.
МАТРИЦЫСТУПЕНЧАТЫЙ ВИД МАТРИЦЫ
О п р е д е л е н и е.
Матрица имеет вид Гаусса,
если:
● матрица является
ступенчатой;
● все опорные элементы равны
единице;
● над опорными элементами
стоят только нули.
Пример.
25.
МАТРИЦЫСТУПЕНЧАТЫЙ ВИД МАТРИЦЫ
Т е о р е м а 1. Любая матрица А может быть приведена к
ступенчатой матрице А1 с помощью элементарных
преобразований строк первого и второго типов.
Т е о р е м а 2. Любая матрица А может быть приведена к
ступенчатой матрице А2 вида Гаусса с помощью
элементарных преобразований строк первого – третьего
типов.
26.
МАТРИЦЫСТУПЕНЧАТЫЙ ВИД МАТРИЦЫ
О п р е д е л е н и е. Матрицы А1 и А2 , построенные по матрице
А с помощью элементарных преобразований, называются,
соответственно, ступенчатым видом матрицы А и видом Гаусса
матрицы А.
О п р е д е л е н и е. Строки и столбцы матрицы A1, в которых
расположены ее опорные элементы, называются базисными
строками и базисными столбцами исходной матрицы.
З а м е ч а н и е. Наборы базисных строк и базисных столбцов и
ступенчатый вид и вид Гаусса у матрицы не единственные.
27.
МАТРИЦЫРАНГ МАТРИЦЫ
О п р е д е л е н и е. Рангом матрицы А называется число
ненулевых строк в ступенчатом виде этой матрицы.
Обозначение: r(A) или rang(A)
Теорема 3. Ранг матрицы не зависит от способа приведения
матрицы к ступенчатому виду.
З а м е ч а н и е. Справедливы неравенства:
0 r(A) min (m, n)
28.
МАТРИЦЫСТУПЕНЧАТЫЙ ВИД МАТРИЦЫ
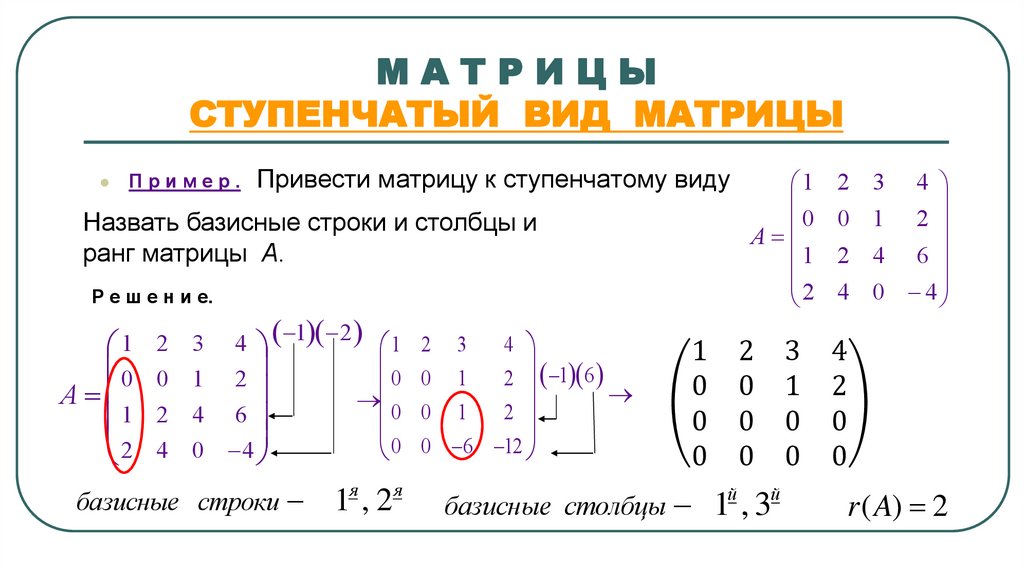
Пример.
Привести матрицу к ступенчатому виду
Назвать базисные строки и столбцы и
ранг матрицы А.
Р е ш е н и е.
1
0
А
1
2
2
0
2
4
3 4 1 2 1
0
1 2
4 6
0
0
0 4
базисные строки
1я , 2 я
2 3
4
0 1
2 1 6
0 1
2
0 6 12
1
0
0
0
базисные столбцы
1
0
А
1
2
2
0
0
0
1й , 3й
3
1
0
0
2
0
2
4
3 4
1 2
4 6
0 4
4
2
0
0
r ( A) 2
29.
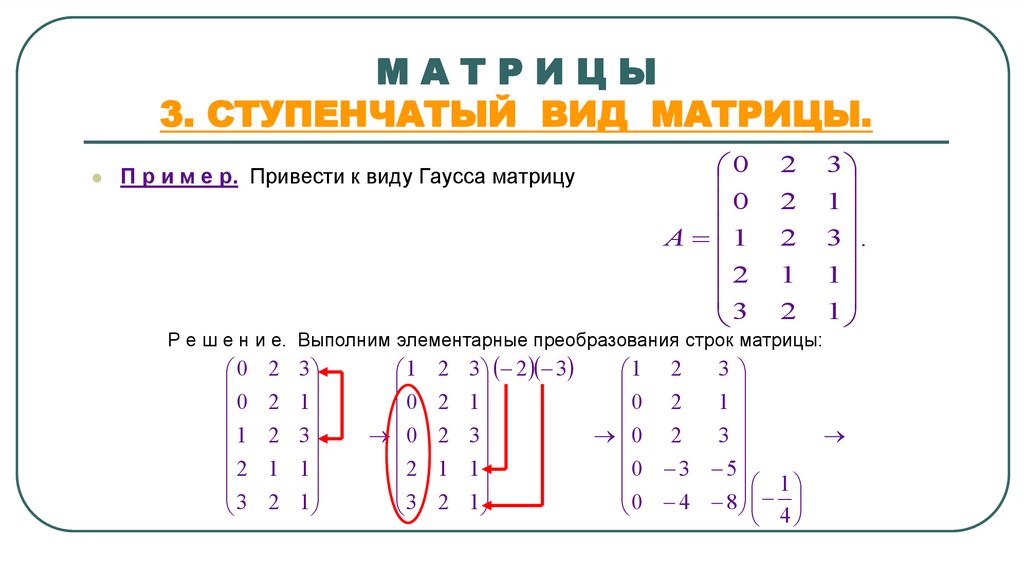
МАТРИЦЫ3. СТУПЕНЧАТЫЙ ВИД МАТРИЦЫ.
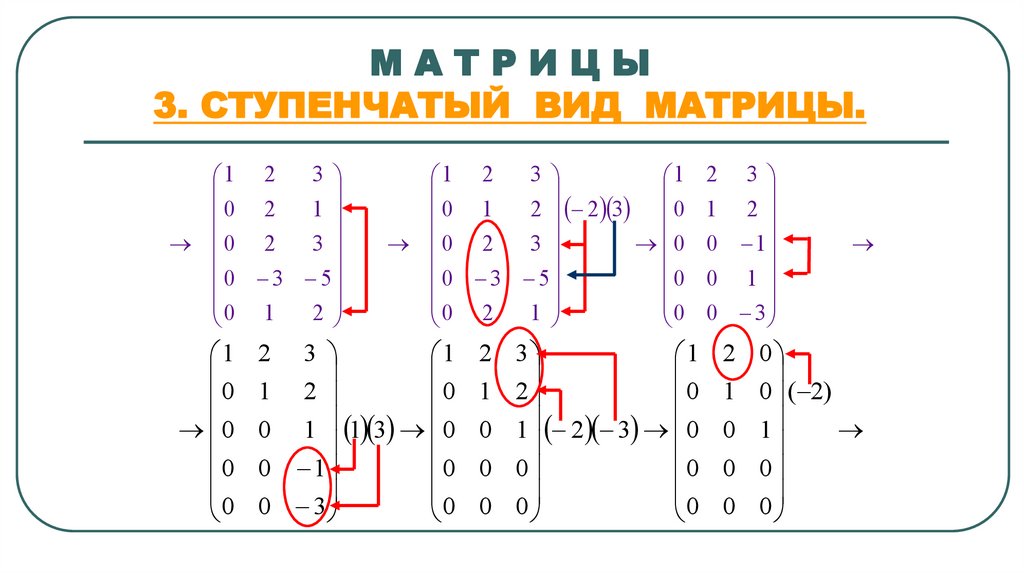
П р и м е р. Привести к виду Гаусса матрицу
0
0
А 1
2
3
2
2
2
1
2
Р е ш е н и е. Выполним элементарные преобразования строк матрицы:
0
0
1
2
3
2
2
2
1
2
3
1
3
1
1
1
0
0
2
3
2
2
2
1
2
3
1
3 .
1
1
3 2 3
3
1 2
1
1
0 2
0 2
3
3
1
0 3 5
1
1
0 4 8 4
30.
МАТРИЦЫ3. СТУПЕНЧАТЫЙ ВИД МАТРИЦЫ.
3
1 2
1
0 2
0 2
3
0 3 5
0 1
2
1
0
0
0
0
2
1
0
0
0
3
1 2
1
2 2 3 0
0 1
0 2
0
3
0 3 5
0
0 2
0
1
3
1
2
0
1 1 3 0
1
0
0
3
2 3
1
1 2
0
0 1 2 3 0
0 0
0
0
0 0
2 3
1 2
0 1
0 1
0 3
2 0
1 0 ( 2)
0 1
0 0
0 0
31.
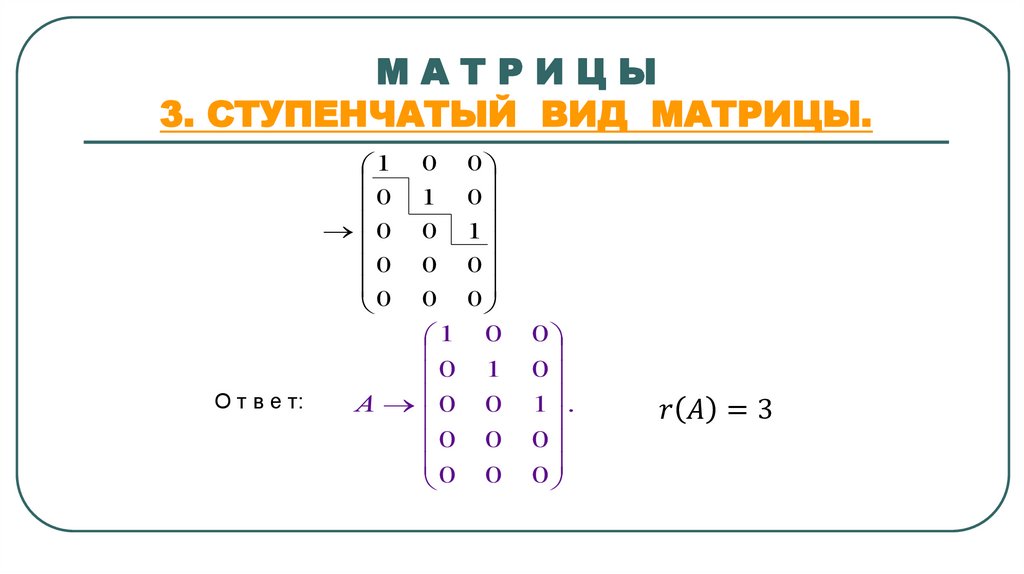
МАТРИЦЫ3. СТУПЕНЧАТЫЙ ВИД МАТРИЦЫ.
1
0
0
0
0
О т в е т:
0
1
0
0
0
1
0
А 0
0
0
0
0
1
0
0
0
1
0
0
0
0
0
1 .
0
0

























 Математика
Математика








