Похожие презентации:
Высшая математика. Глава 1. Элементы линейной алгебры. Матрицы и определители
1. Высшая математика Глава I. Элементы линейной алгебры
ЛЕКЦИЯ 1Матрицы и
определители
2. Литература
• Письменный Д.Т. Конспект лекций по высшейматематике. Часть 1. – М.: Айрис-Пресс, 2009.
• В. С. Шипачев. Высшая математика. Базовый
курс : учеб. пособие для вузов. М.: Юрайт,
2011.
• Лунгу, К. Н. Сборник задач по высшей
математике. 1 курс. — М.: Айрис-пресс, 2009.
3.
• Большой объем новой информации : 1, 2, 3, 4 семестры +специальные курсы.
• Отчётность: в зависимости от семестра: ДЗ, ТР, КР, СР, зачет,
экзамен.
• Задавайте вопросы по ходу лекций и на ПЗ.
• Подготовка к ПЗ, зачетам и экзаменам.
• Работа с учебниками.
• Консультации в семестре.
• Консультации в сессию.
• Ответы на практических занятиях.
• Тесты в «Прометее».
• Элементарная математика.
• Участие в олимпиадах.
4.
•В наши дни применительно к образованию выдвигается напервый план задача – научить умению учиться.
учиться
•Учеба – серьёзный труд.
•Школа, вуз – специально отведенное для этого время.
•Успевать надо все – спорт, театр, книги, …
•Дальше специального времени не будет, хотя учиться
придется всю жизнь.
5. Термины
• Студент (studiosus) в переводе с латыни – старательный,усердный, устремленный, прилежный.
• Термин «Математика» происходит от греческого слова
«mathein» [матейн] – учиться, познавать.
• «Математика – наука о количественных отношениях и
пространственных формах действительного мира». Ф. Энгельс,
«Диалектика природы», 1877 г.
• Университет (universitas) – в переводе с латинского – свернутые
воедино, совокупность людей, объединенных общей целью
(учиться).
• Инженер – даровитый, талантливый. В первоначальном
понятии это относилось к человеку, который постоянно что-то
придумывал, изобретал. К настоящему времени…
трансформировалось… в специалиста в какой-то области
техники с высшим образованием.
6.
• Математика – существеннейшая составная частьчеловеческой культуры, она является ключом к
познанию окружающего мира, базой научнотехнического прогресса и важной компонентой
развития личности.
• «Царица наук» – так нередко именуют ее,
стоящую в особом ряду среди всех прочих
достижений человечества.
7.
• Человек, получивший глубокое фундаментальное образование,способен комплексно, системно оценить последствия тех или иных
управленческих решений и обеспечить для условия устойчивого
развития общества.
• Кроме того, фундаментальное образование – основа для
последующего обучения на протяжении всей жизни, что имеет
чрезвычайно большое значение в современном обществе, в условиях
быстрой смены технологий.
• Чтобы человечество развивалось, причем развивалось плодотворно,
нужны не только лучшие умы, но и свежие идеи. А для этого
необходимы креативные люди с необычным мышлением, широким
кругозором, гибким умом.
• Чтобы все это было в человеке, нужно чтобы он совершенствовал
себя.
• Математика нужна для интеллектуального развития личности, она
содержит в себе черты волевой деятельности, умозрительного
рассуждения и стремления к эстетическому совершенству. Ее
основные и взаимно противоположные элементы - логика и интуиция,
анализ и конструкция, общность и конкретность.
• Благодаря изучению высшей математики приобретается философский
аналитический ум и способность к самостоятельному мышлению.
8.
• В рейтинге систем высшего образования, ежегодносоставляемого ЮНЕСКО, Россия опустилась за
последние 25 лет с 3 на 33 место.
• 1990 г. – 3 место;
• 2001 г. – 19 место;
• 2007 г. – 27 место;
• 2015 г. – 33 место.
9.
• «Учеба – серьёзный труд.• Без собственных усилий ничего не выйдет. Можно купить какие
угодно книги, обучающие программы (английский во сне),
можно нанять прекрасных репетиторов, которые всё разжуют и
положат в рот. Но глотать нужно самому! Учиться должен сам.
Купить можно диплом об образовании, но не само образование.
• Преподаватель - ваш помощник, его задача – разбросать семена
знаний, ваша задача – их поймать.
• Дача знаний не самое важное. Запомните – хорошо. После
экзамена забудете – ничего – как-то проживёте. Самое важное –
подтолкнуть человека, чтобы он начал думать, размышлять (а в
каждом из вас это заложено).
• Домашняя подготовка, самостоятельная работа. Иначе на
практическом занятии нечего будет делать (без знаний нет
творчества).
• Книга! (конспект – не учебник, а канва изложения материала).
• Психологически эффективность самообразования объясняется
очень просто – полученные самостоятельно знания и навыки
человек ценит куда больше, чем те, которые преподнесли ему на
блюдечке.»
10. Кванторы, обозначения и сокращения
КВАНТОРЫ, ОБОЗНАЧЕНИЯ ИСОКРАЩЕНИЯ
11.
12. 1. Матрицы
13.
Термин «матрица»ввел английский математик
Джеймс Джозеф Сильвестр.
1814–1897
«Математика – музыка разума».
Джеймс Джозеф Сильвестр
14. Матрицы
Матрицей размера m n называетсяпрямоугольная числовая таблица,
состоящая из m строк и n столбцов.
a11 a12
a
a22
21
...
...
a
m1 am 2
...
...
aij
...
Числа аij –
a1n
элементы
a2 n
(1.1) матрицы, где
... i – номер строки
amn
j – номер столбца.
A, B, C
Обозначения:
… или (aij), (bij),
(cij) ...
15. Примеры
Примеры
0
А
1
2
2
111
В 3 3 3
5 5 5
3
3
4
7
9 2
С 2 0
3 0
3
2
16.
1.1. Виды матриц17.
1. Прямоугольная матрицаМатрица, в которой число строк не равно числу
столбцов, называется прямоугольной.
0 1 2
A2 х 3
1 7 0
18. 2. Матрица-строка и матрица-столбец
Матрица-строка (1 n)A a1 a2 ... an
Матрица-столбец (n 1)
b1
b
B 2
...
bn
19. 3. Нулевая матрица
Матрица, все элементы которойравны нулю, называется нулевой.
Обозначается буквой О.
Нулевая
0 ... 0
Оmxn ... ... ...
0 ... 0
20. 4. Квадратная матрица (m=n) (1.2)
a11 a12 .... a1n4. Квадратная
.... a 2 n (m=n)
a 21 a 22 матрица
A
.... .... ..... .....
a
a
.....
a
n2
nn
n1
(1.2)Матрица,
у которой число строк равно числу
столбцов называется квадратной.
Квадратную матрицу размера
матрицей n - го порядка.
n n
называют
21. Примеры
Квадратные матрицы5 11
А 2 4 2
3 1 3
3-го
порядка
7 2
B
1 5
2-го
порядка
22. 5. Диагональная матрица
a11 0 0 ... 0 0... 0a
11 0 a 0 ... 0
А 0 0 a22 022 ...a 0... 0diag
(1. 3a
) , a ,..., a .
33
11 22
nn
... ... ... ... ... ... ...... ...
0 0 0 0 ... 0 a ... a
nn nn
Элементы квадратной матрицы с одинаковыми
индексами от a11 к ann, образуют главную
диагональ.
Квадратная матрица, у которой все элементы,
кроме элементов главной диагонали, равны нулю,
23.
Примеры1 0 0
А 0 3 0
0 0 5
7 0
B
0 5
Диагональная матрица 3-го порядка Диагональная матрица 2-го порядка
24.
6. Единичная матрицаДиагональная матрица, у которой каждый элемент
главной диагонали равен единице,
называется единичной.
единичной
Обозначается буквой Е или I.
25.
10
Е2 diag 1, 1 0 1
Еn diag 1, 1, ...,1
1 0 0
Е3 diag 1, 1, 1 0 1 0
0 0 1
25
26. Примеры
7. Треугольная матрицаКвадратная матрица называется треугольной, если
все элементы, расположенные по одну сторону от
главной диагонали, равны нулю.
Примеры
верхнетреугольная
111
А 0 3 3
0 0 5
нижнетреугольная
7
B
1
0
5
27.
Матрица, полученная из данной заменой каждойеё строки столбцом с тем же номером, называется
матрицей транспонированной к данной.
Обозначается AT.
Пример
0 3
А 1 4
2 5
Þ
0
1
2
А 3 4 5
T
(АТ)Т=А
28.
9. Симметрическая матрица• Если AT = A то матрица A называется симметрической.
симметрической
Пример
1
2
3
1 2 3
Т
С 2 3 0 Þ С 2 3 0 C
3 0 5
3 0 5
29.
10. Кососимметрическая матрицаКТ = - К
Пример
0 2 3
К 2 0 1
3 1 0
30. 11. ТРАПЕЦИЕВИДНАЯ ФОРМА МАТРИЦЫ
- aii 0.- aij - любое, j>i.
31. 12. Равные матрицы
Две матрицыA= (aij) и B=(bij)
называются равными,
равными
если
1) Размеры
матриц
совпадают
2) Соответствующие
элементы матриц
равны:
aij=bij,
i=1,…,m; j=1,…,n.
32. 1.2. Операции над матрицами
33. Сумма матриц
Сложение и вычитание матриц возможно, еслиэти матрицы имеют одинаковый размер.
Суммой матриц A=(aij) и B=(bij)
размера m n называется матрица C=(cij) размера m n,
каждый элемент которой равен сумме соответствующих
элементов матриц A
и B.
cij aij bij , ( i 1 , m ; j 1 , n )
34. Сумма матриц
Пример2 3 4 5 2 4 3 5 6 2
A B
1 0 2 8 1 2 0 8 1 8
35. Пример
Найти разность матриц33
0 2
A 1 0 и B 3 1 .
1 2
2 2
3 3 0 2 3 0 3 2 3 1
A B 1 0 3 1 1 3 0 1 4 1 .
1 2 2 2 1 2 2 2 1 0
36. Умножение матрицы на число
Произведением матрицы A=(aij) и числаназывается матрица того же размера,
элементы которой равны aij.
2
1 2 3
А 0 0 4 Þ2 А 0
0 0 5
0
4 6
0 8 .
0 10
37.
Свойства суммы матриц иумножения матрицы на число
38.
Пусть A, B, C, О ─ матрицыодного размера, а , , - числа.
1. Коммутативность суммы матриц
A B B A
39.
2. Ассоциативность сложения матриц( A B) C A ( B C )
40.
3. Дистрибутивность( A B) A B
число.
A A A ,
, - числа.
41.
4.А+О=А
О – нулевая матрица, того же размера, что и А.
42. Произведение матриц
43. Умножение матриц выполнимо, если число столбцов первой матрицы равно числу строк второй.
44.
Умножениестроки на столбец
b1
b2
A a1, a2 , , an , B .
b
n
AB a1b1 a2b2 anbn .
Пример
1
A 3 , 1 , 4 , B 0 .
3
AB 3 1 1 0 4 3 15.
45. Умножение матрицы на столбец Каждая строка матрицы скалярно умножается на столбец
3 1 2 8 3 8 1 7 2 2 214 2 0 7 4 8 2 7 0 2 46
5 6 1 2 5 8 6 7 1 2 4
46. Умножение матриц
Произведением матриц A=(aij) (размера m p)B=(bij) (размера p n) называется матрица
C=(cij) (размера m n), элементы cij которой
вычисляются как скалярное произведение i – й строки
матрицы A и j – го столбца матрицы B.
и
Умножение матриц
b1 j
b2 j
a a a
i1 i 2
ip
b
pj
cij
.
47. Пример
2 6 1 2 0Найти произведение матриц
.
1 2 0 1 3
2 2 6 ( 1)
2 0 6 3
2 1 6 0
1 1 ( 2) 0 1 2 ( 2) ( 1) 1 0 ( 2) 3
2 2 18
1 4 6
48.
A B B AВообще говоря, если произведения АВ и ВА существуют, то АВ ВА.
Если АВ=ВА, то такие матрицы называются перестановочными.
Пример.
48
49. УМНОЖЕНИЕ СТОЛБЦА НА СТРОКУ
7 57 2
7
0 2 5 3 0 2
0
5
4
4 2 4 5
14 35 21
0
0
0
8 20 12
7 3
0 3
4 3
50.
При условии, что операции в обеих частяхравенств выполнимы, справедливы
следующие свойства.
Свойства произведения матриц
1. А · О = О;
2. А · Е = А;
3. А · В ≠ В · А;
4. α (АВ) = (αА) · В = А · (αВ);
5. АВС = (АВ) · С = А · (ВС);
6. А (В + С) = АВ + АС;
7. (А · В)Т =ВТ · АТ.
51. 2. Определители
52.
Вильгельм ГотфридЛейбниц
(1646-1716) — саксонский
философ, логик, математик,
механик, физик, юрист,
историк, дипломат,
изобретатель и языковед.
Понятие «определитель»
принадлежит Г. Лейбницу
(1678).
53.
Определитель (детерминант) –числовая характеристика квадратной матрицы.
Обозначения определителя матрицы А:
|A|, det A, .
54. Невырожденная матрица
• Квадратная матрица А называетсяневырожденной,
невырожденной если её определитель
det А 0.
• В противном случае (det А = 0) матрица
А называется вырожденной.
55. Квадратной матрице А порядка n можно сопоставить число det A, называемое ее определителем, следующим образом: 1. n = 1. А = (a1); det A = a1
2. n = 2.a11
| A |
a21
a12
a11 a22 a12 a21
a22
• Вычисление определителя 2-го порядка
Квадратной
матрице
А порядка n можно сопоставить
иллюстрируется
схемой:
число det A, называемое ее определителем, следующим
образом:
1. n = 1. А = ( a1); det A = a1
Пример.
56. 3. n = 3. Для вычислении определителя 3-го порядка используют правило треугольников (Саррюса).
a11a12 a13det A a21a22 a23 a11a22 a33 a12 a23a31
a31a32 a33
a13a21a32 a31a22 a13 a32 a23a11 a33a21a12
57.
**
*
*
*
*
* *
* *
* *
*
*
*
*
*
*
58.
Пример. Вычислитьопределитель третьего порядка
5 2
= 3
6
1
1
4
0
3
=5•1•(-3) +
+(-2)•(-4)•6 +
+ 3•0•1–6•1•1–
–3•(-2)•(-3) –
– 0•(-4)•5 =
–15+48–6–18=
=48–39=9.
59.
Пример. Вычислить определитель с помощьюправила диагоналей
5 2
= 3
6
1
0
- -
1
4
3
-+ + +
=5•1•(-3) +
+(-2)•(-4)•6 +
+ 3•0•1–(6•1•1+
+ 0•(-4)•5+
+3•(-2)•(-3)) =
–15+48–(6+18)=
=33–24=9.
60. Определитель произвольной треугольной матрицы равен произведению элементов главной диагонали
61.
Минор элемента аi j• Минором некоторого элемента aij квадратной матрицы
А n-го порядка называется определитель n –1-го
порядка матрицы, полученной из исходной путем
вычеркивания из А строки и столбца, на пересечении
которых находится выбранный элемент aij , минор
обозначается Мij.
3
7
А 0
5
2
3
5
7
5
4
6
9
a23=4
1
2
2
4
3 2 1
M23 0 5 2 60 20 0 250 0 42 13
5 7 4
M31=5
M14=11
62.
Алгебраическое дополнение Aik• Алгебраическим дополнением элемента aik
квадратной матрицы А называется число Аik :
Для предыдущего примера:
63.
ФОРМУЛА ЛАПЛАСАТеорема. Определитель матрицы равен сумме
произведений элементов любого ее ряда на
соответствующие им алгебраические a11 a12 a13
дополнения.
a21 a22 a23
a
Разложение определителя по 31
a32
элементам первой строки:
a33
det A a 11 A11 a 12 A12 a 13 A13 .
Пьер-Симоон, маркиз де
Лаплаос (1749 - 1827) —
французский математик,
механик, физик и астроном
64.
2 1 14 3
1 1
2 4 3 2
2
17 12
17 12
11 17 12
1 1
11
2( 48 51) 2(12 17) 11(3 4)
4 3
6 10 11 5.
4
1
0
3
4
1
3
4 1
1 3
2 2 3 1 2 5
5
2 3 0 1
3
1
2
3
5 0 5
5 0 0 5
3
5
2
4
2(5 10 5 ( 14)) 2(50 70) 2 120 240
65. ПРАВИЛО ЧУЖИХ ДОПОЛНЕНИЙ
• Сумма произведений элементов любого ряда кв. матрицына
алгебраические
дополнения
соответствующих
элементов другого ее параллельного ряда равна нулю.
66.
СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ1. Транспонирование матрицы не меняет значения ее
определителя.
det A det A
T
3 5 6 3 4 5
4 2 1 5 2 3
5 3 2
6 1 2
67.
Свойства определителей2. При перестановке двух параллельных рядов определитель
меняет знак.
3. Если соответствующие элементы двух параллельных рядов
равны или пропорциональны, то определитель равен 0.
4. Общий множитель элементов какого-либо ряда можно
вынести за знак определителя.
5. Определитель не изменится, если к элементам одного ряда
прибавить соответствующие элементы параллельного ряда,
умноженные на одно и то же число.
6. Определитель матрицы, содержащей целый ряд из нулей,
равен нулю.
7. detЕ 1
8. det( A B ) det A det B
68.
9. Если элементы какой-либо ряда квадратной матрицыА состоят из двух слагаемых, то определитель А равен
сумме определителей двух матриц, различающихся
между собой только элементами этого ряда, бывшими
ранее отдельными слагаемыми.
а11
а11
а 21
а 21
а31
а31
а12
а13
а 22
а 23
а32
а33
а11
а 21
а31
а12
а13
а 22
а 23
а32
а33
а11
а 21
а31
а12
а13
а 22
а 23 .
а32
а33
69.
«А математику уже затем учитьследует, что она ум в порядок
приводит».
М. В. Ломоносов
Спасибо за внимание!










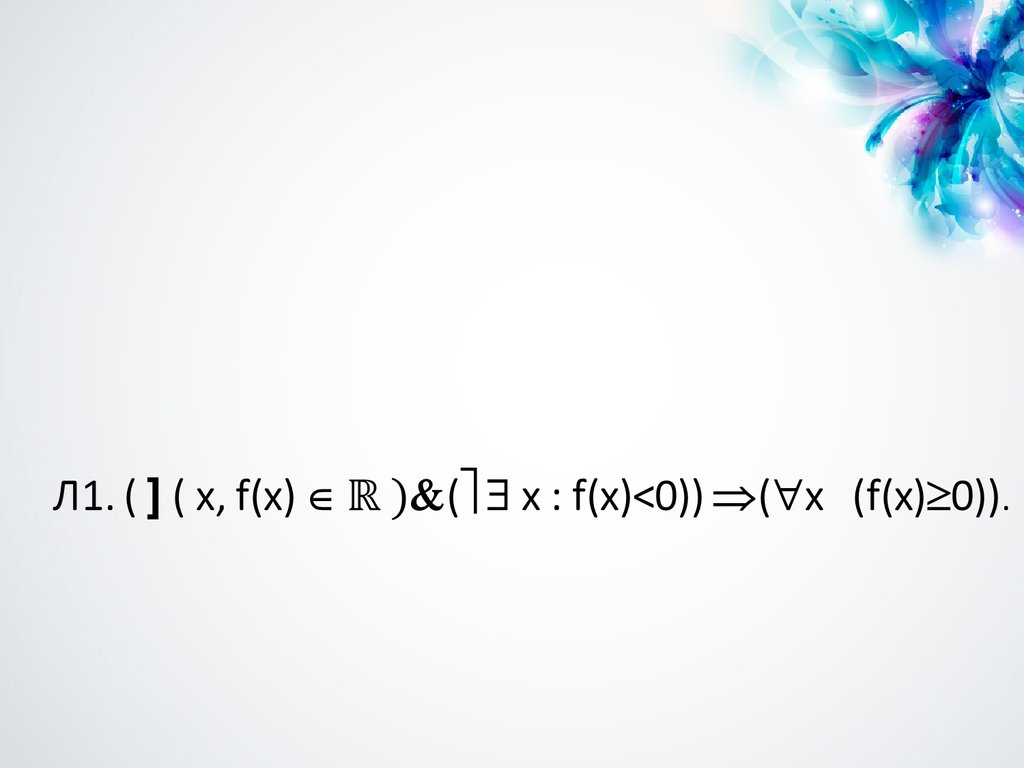













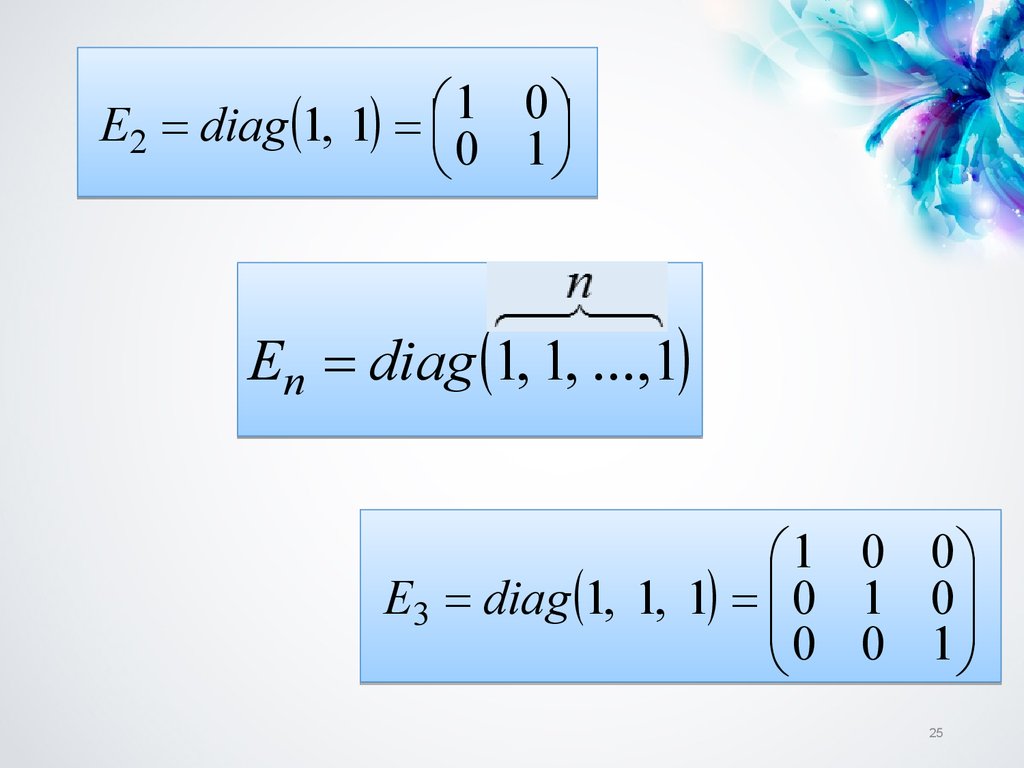































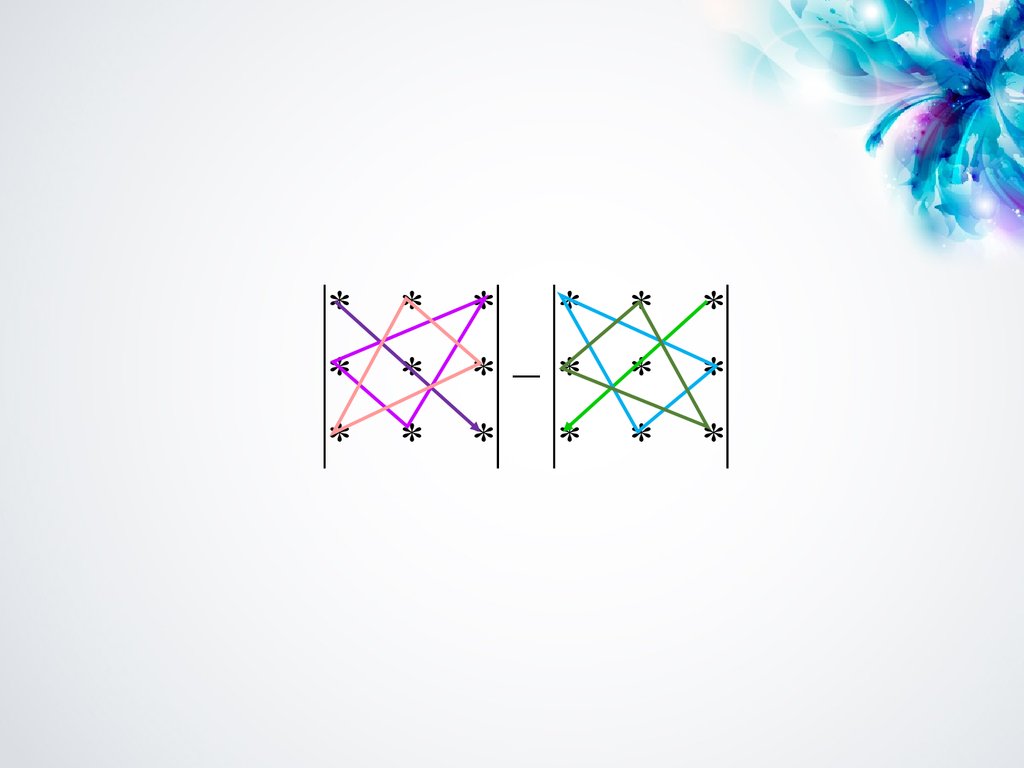






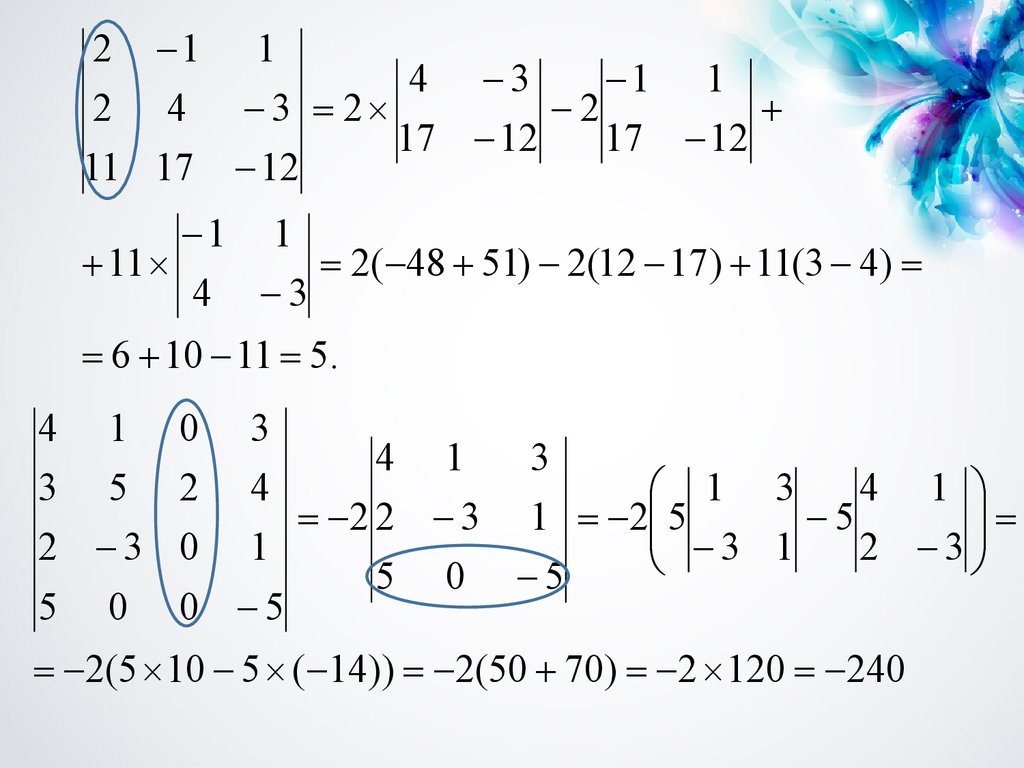





 Математика
Математика








