Электричество и магнетизм. Лекция 13. Электромагнитная индукция

1.

Электричество и магнетизм
Лекция 13
Электромагнитная индукция
24 ноября 2021 года
Лектор: доцент НИЯУ МИФИ
Ольчак Андрей Станиславович

2.

Основные законы магнитостатики
Основные законы электростатики и магнитостатики
E
0
B 0
E 0
B 0 j

3.

Магнитный диполь
Магнитный дипольный момент
E
B
n
S
I
p m ISn
0 3 p m r r
B
pm
3
2
4 r
r
3 d r r
E
d
3
2
4 0 r r
1

4.

Контур с током в магнитном поле
B
n
M
pm
O
I
p m ISn
B
B
B
F p m B pmx
pmy
pmz
x
y
z
Момент силы Ампера
M p m B
w pm B cos p m B
Аналогия с электрическим диполем: w p E
Как правило свободный магнитный диполь втягивается в область
более сильного магнитного поля.
Формулы для момента силы и энергии магнитного диполя
одинаковы для однородного и неоднородного полей.

5.

Опыт Фарадея
(электромагнитная индукция)
См. «Физика в опытах», часть 3

6.

Закон электромагнитной индукции
Опыты Фарадея.
ЭДС индукции
29 августа 1831 г. М. Фарадей
открыл явление электромагнитной
индукции – возникновение
электрического поля и
электрических токов в контуре при
изменении потока магнитного
поля.
Майкл Фараде́й
1791 - 1867

7.

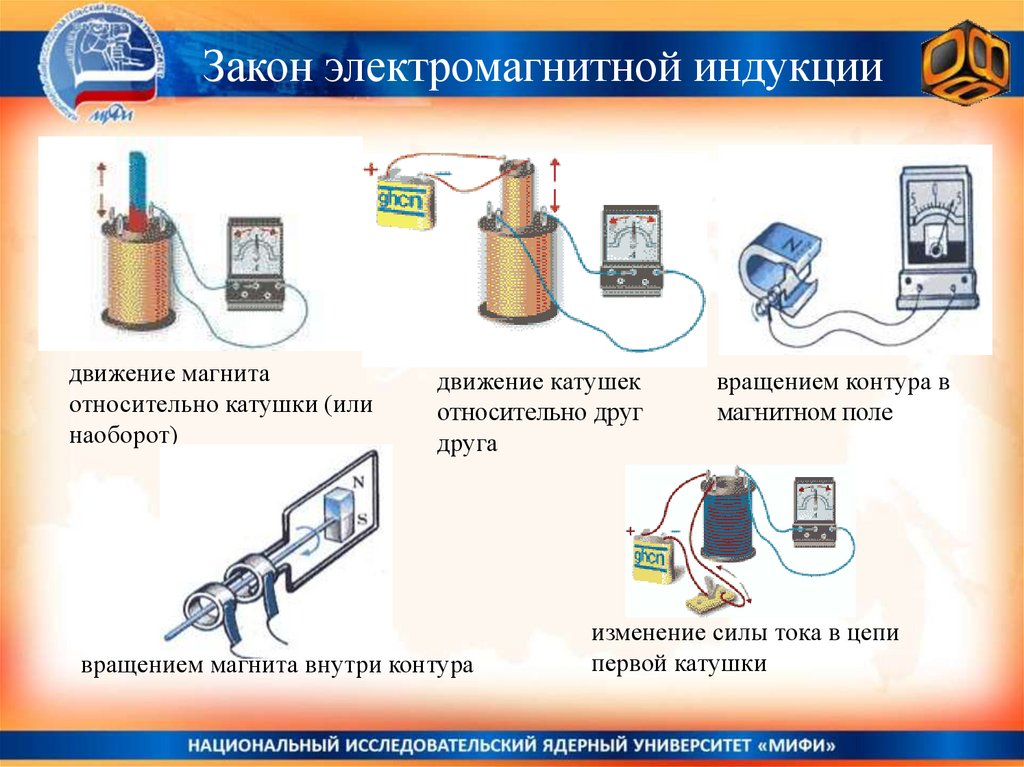
Закон электромагнитной индукции
движение магнита
относительно катушки (или
наоборот)
движение катушек
относительно друг
друга
вращением магнита внутри контура
вращением контура в
магнитном поле
изменение силы тока в цепи
первой катушки

8.

Закон электромагнитной индукции
Результаты опытов Фарадея
В замкнутом контуре, не содержащем ЭДС, появляется
индукционный ток, если:
1. Контур или его часть движутся в магнитном поле так, что
меняется магнитный поток через контур;
2. Контур неподвижен, но меняется магнитное поле в
которое он помещен (создающая поле катушка движется
или меняется ток катушки) и – как следствие – меняется
магнитный поток через контур .
d
i
dt
B dS
S
Математическая
формулировка
Э.Х.Ленца:

9.

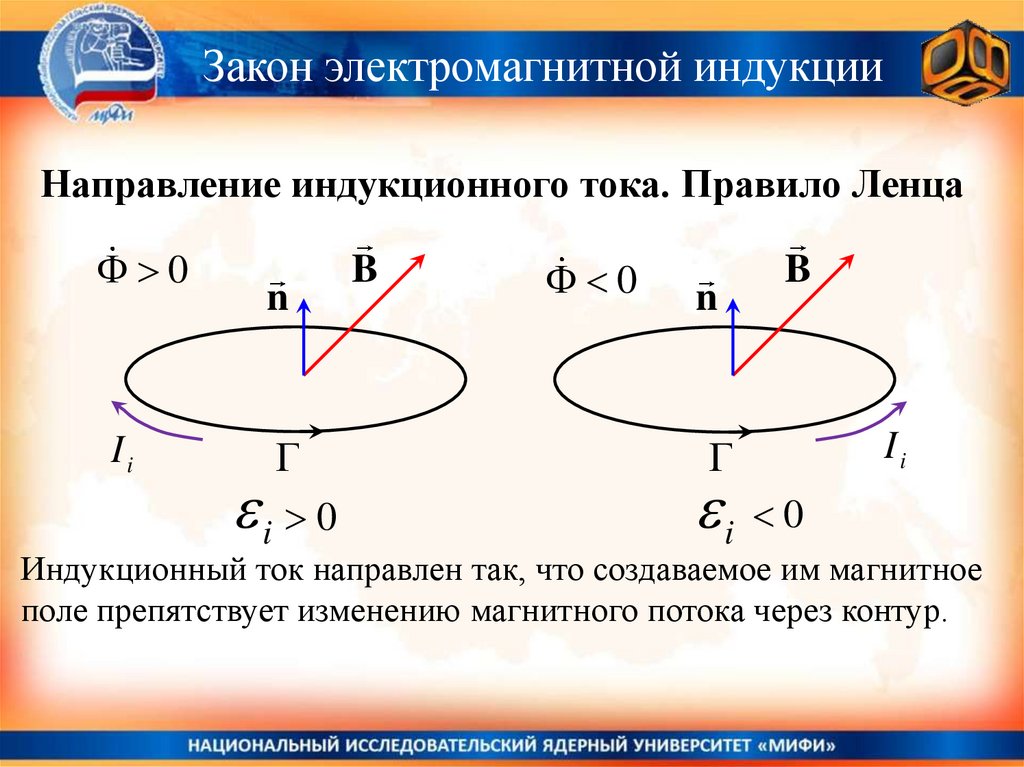
Закон электромагнитной индукции
Направление индукционного тока. Правило Ленца
0
Ii
n
i 0
B
0
n
B
i 0
Ii
Индукционный ток направлен так, что создаваемое им магнитное
поле препятствует изменению магнитного потока через контур.

10.

Закон электромагнитной индукции
Bсоб
Bсоб
Индукционный ток направлен так, чтобы противодействовать
причине его вызывающей.

11.

Закон электромагнитной индукции
Физические механизмы электромагнитной индукции
1. Движется контур или его часть
u - дрейфовая скорость
носителей тока
n
B
u
dl
dr
dS
d 2S
v
d l dr
v - скорость движения
участка проводника dl
Fстор q v u B
q v B q u B

12.

Закон электромагнитной индукции
i
Aстор
q
v B d l
dr
dt B d l
dr B d l d l dr B d 2 Sn B
B
n
u
dl
dr
dS
i
d 2S
v
d l dr
d 2 Sn
B
dt

13.

Закон электромагнитной индукции
2. Контур неподвижен, меняется магнитное поле
F q v B т.к. v 0
B const E 0
Гипотеза: меняющееся магнитное
поле В(t) генерирует вихревое
электрическое поле!
i
B
E
t
E d l E dS
S
B
d
dS B dS
t
dt S
S
d
dt

14.

Закон электромагнитной индукции
B
E
t
i
B const E 0
E d l E dS
S
d
B
d
dS B dS
dt
t
dt S
S

15.

Электромагнитная индукция
Применение для измерения магнитного поля или
протекающего по цепи заряда
N
i
i 1
d
i
dt
d
dq
R
– полный магнитный поток через
катушку (потокосцепление)
dq i
1 d
I
dt R
R dt
0
1
NBS
q d
R
R
R
qR
B
NS

16.

Электромагнитная индукция
Применение для
нагревания
Токи Фуко

17.

Электромагнитная индукция
Главное применение – генерация электроэнергии

18.

ИНДУКТИВНОСТЬ
и
САМОИНДУКЦИЯ

19.

Явление самоиндукции
Индуктивность контура
B
Ф ~ B ~ I => Ф = LI
L [Тл*м2/А = Гн (Генри)] -
I
Контур из тонкого
проводника
индуктивность контура = коэффициент
пропорциональности между током в
контуре и создаваемым им магнитным
потоком через сам контур.
Note 1. В отсутствие ферромагнетиков L
зависит только от геометрии и площади
контура (ну и немножко от магнитной
проницаемости среды)
Note 2. L > 0.

20.

Явление самоиндукции
Индуктивность соленоида
B 0 nI const
l
S
N nlBS
V lS
H nI
nVB
nV 0 nI 0 n 2VI
LI
L 0 n 2V
0
Гн м

21.

Явление самоиндукции
ЭДС самоиндукции
Самоиндукция = изменение тока в контуре, вызванное изменением
потока собственного магнитного поля через контур.
d s
dt
Ф = LI =>
dI
L
dt
L const
По правилу Ленца, возникающая ЭДС самоиндукции направлена
против порождающей ее причины.
Если dI/dt>0 ЭДС будет направлена против усиливающегося тока
Если dI/dt>0 ЭДС будет поддерживать ослабевающий ток

22.

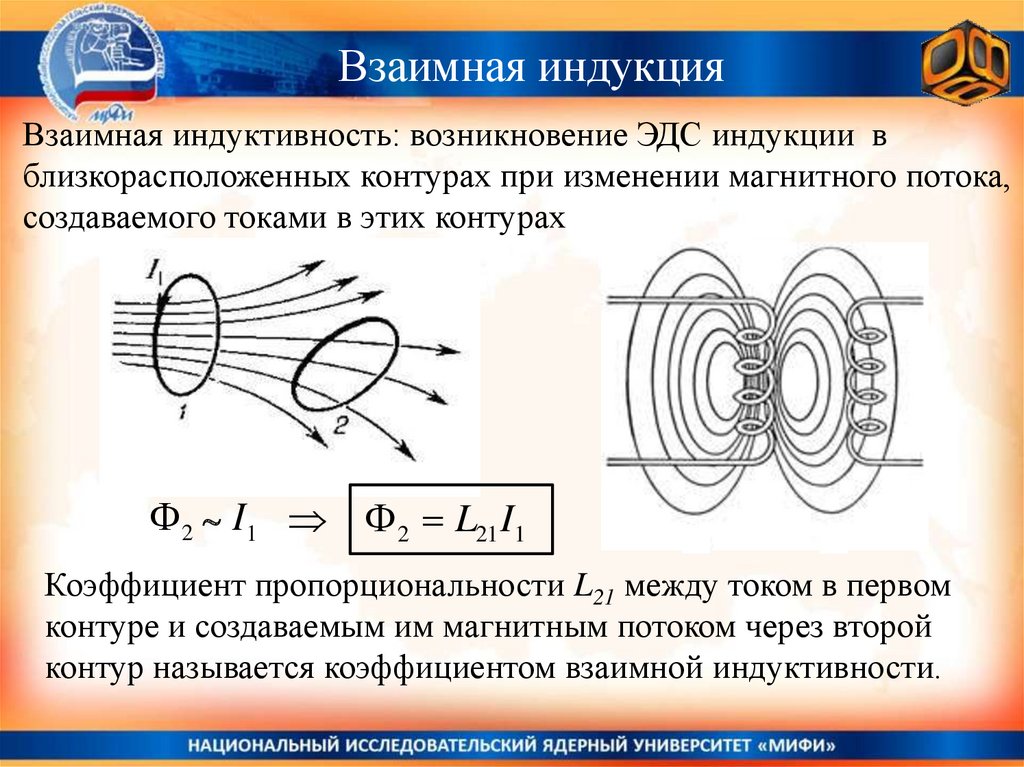
Взаимная индукция
Взаимная индуктивность: возникновение ЭДС индукции в
близкорасположенных контурах при изменении магнитного потока,
создаваемого токами в этих контурах
2 I1 2 L21 I1
Коэффициент пропорциональности L21 между током в первом
контуре и создаваемым им магнитным потоком через второй
контур называется коэффициентом взаимной индуктивности.

23.

Взаимная индукция
2 L21 I1
=> 1 L12 I 2 Контуры 1 и 2 называются
Теорема взаимности
индуктивно-связанными.
L12 L21
Note 1. Коэффициенты L12 и L21 зависят от формы, размеров и
взаимного расположения контуров.
Note 2. Коэффициенты L12
и L21 могут принимать как
положительные, так и
отрицательные значения
n1
n2
L12 0
n1 n 2
L12 0

24.

Взаимная индукция
Теорема взаимности. Доказательство (для
самостоятельного ознакомления) с использованием
понятия векторного потенциала магнитного поля
R r r1
1 n1
I1
dr1
r1
n2
R
r
O
2
L12 L21
dr1 R
R3
Покажем, что: B1 r A1
0 I1 dr1
где A1 r
4
R
0 I1
B1 r
4

25.

Взаимная индукция
Теорема взаимности. Доказательство (для
самостоятельного ознакомления) с использованием
понятия векторного потенциала магнитного поля
L12 L21
1 n1
I1
dr1
n2
R
r1
2
B1 A1
r
O
2 B1 dS2 A1 dS2
S2
S2
L21 I1
A1 dr2

26.

Взаимная индукция
Ф1 = Ф11 + Ф12 => ε1 = dФ1/dt = L11dI1/dt + L12dI2/dt =>
Ф2 = Ф21 + Ф22 => ε2 = dФ2/dt = L21dI1/dt + L22dI2/dt =>
Фi = ΣkФik => εi = Σk LikdIk/dt = LikdIk/dt
Коэффициенты Lik пропорциональны числу витков в катушке i
=> способ преобразования амплитуды переменного напряжения
(трансформатор)

27.

Дистанционный курс общей физики НИЯУ МИФИ
Спасибо за внимание!
Следующая лекция
1 декабря

28.

Примеры решения задач
Пример 1. Найти работу, которую нужно совершить, чтобы
переместить по рельсам перемычку длиной l на расстояние s с
постоянным ускорением a. Индукция магнитного поля B
перпендикулярна плоскости, в которой находятся перемычка
и рельсы. Ёмкость конденсатора равна C, а сопротивлением
рельсов и перемычки можно пренебречь.
B
C
a
l
s

29.

Примеры решения задач
B
C
l
a
FA
F
s
I
q Blv
dq
dv
I
Bl
Bla
dt
dt
FA IBl B 2l 2 aC const
F FA
d
dx
i Bl Blv
dt
dt
q
i U Blv
C
A B 2l 2 aCs

30.

Примеры решения задач
Пример 2. Найти взаимную индуктивность на единицу длины
двух бесконечных коаксиальных соленоидов, имеющих
радиусы R1 и R2 и число витков на единицу длины n1 и n2,
соответственно.
а) I 2 const
R1
R2
B2 0 n2 I 2
1 R12 n1 B2
R n 0 n2 I 2
2
1 1

31.

Примеры решения задач
R1
R2
1 0 R12 n1n2 I 2
1 L12 I 2
L12 0 R12 n1n2
б) I1 const
0 R12 n1n2 I1
B1 0 n1 I1
2 R12 n2 B1
2 L21 I1
L21 0 R12 n1n2

32.

Закон электромагнитной индукции
Пояс Роговского
j