Способы преобразования эпюра Монжа

1. Способы преобразования эпюра Монжа

1. Способ замены плоскостей проекций - изменение
положения одной из плоскостей проекций при
неизменном положении геометрического образа
2. Способ вращения - изменение положения
геометрического объекта до требуемого
3. Изменение самого способа проецирования.

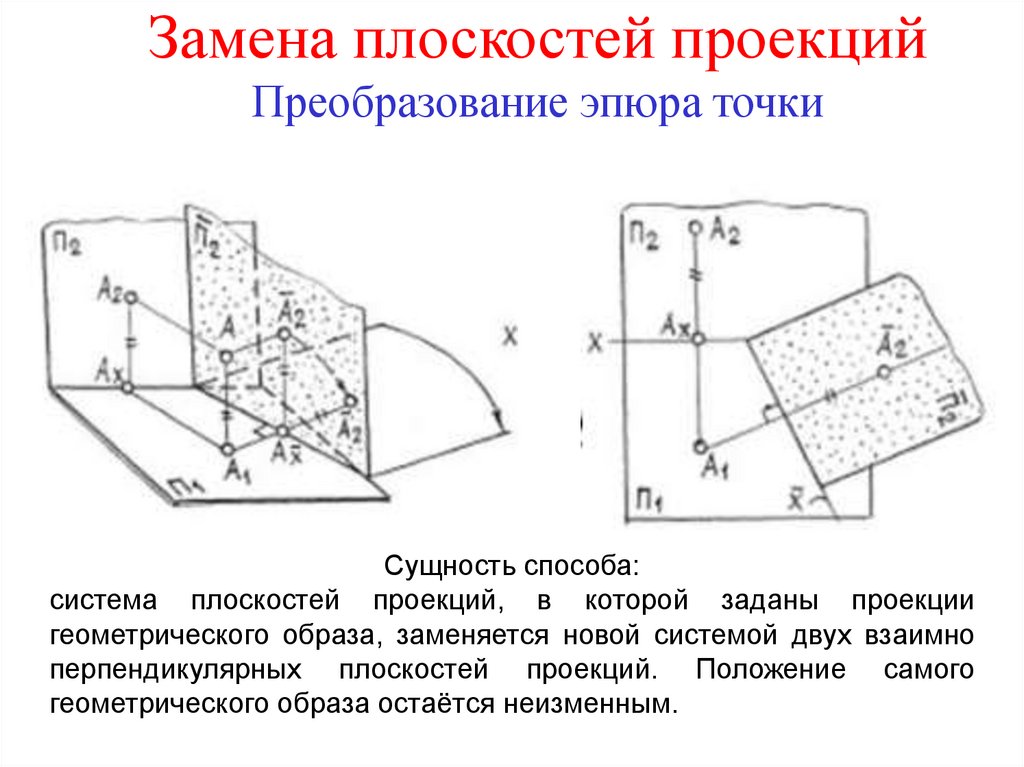
2. Замена плоскостей проекций Преобразование эпюра точки

Сущность способа:
система плоскостей проекций, в которой заданы проекции
геометрического образа, заменяется новой системой двух взаимно
перпендикулярных плоскостей проекций. Положение самого
геометрического образа остаётся неизменным.

3. Замена плоскостей проекций Преобразование эпюра точки

А2
х П2
П
А2
А1
Расположение новой оси определяется
задачей. Сохраняется расстояние от
заменяемой оси до заменяемой проекции
точки.
П1
П2
х

4.

Преобразование эпюра прямой

5. Замена плоскостей проекций Преобразование прямой общего положения в прямую уровня

А2
В2
х
П2
П1
А1
Новую ось проводим параллельно
какой-либо проекции прямой.
На новую плоскость прямая
проецируется в натуральную
величину
В1
А2
П1
В2
П2
х

6. Замена плоскостей проекций Преобразование линии уровня в проецирующую прямую

h2
x П2
П1
h2
h1
Новую ось х проводим перпендикулярно
горизонтальной проекции горизонтали
П1
П2
x

7. Преобразование прямой общего положения (АВ) в проецирующую прямую

Решение включает последовательную
замену двух систем плоскостей
проекций.
1. Первоначально расположим новую
плоскость проекций
параллельно
прямой (А,В).
Получим
систему
плоскостей
проекций, относительно которой
прямая (А, В) будет линией уровня.
2. При последующей замене новую плоскость проекций
расположим уже перпендикулярно линии уровня (А,В).
В результате будем иметь систему плоскостей проекций,
относительно которой (А,В) – проецирующая прямая.

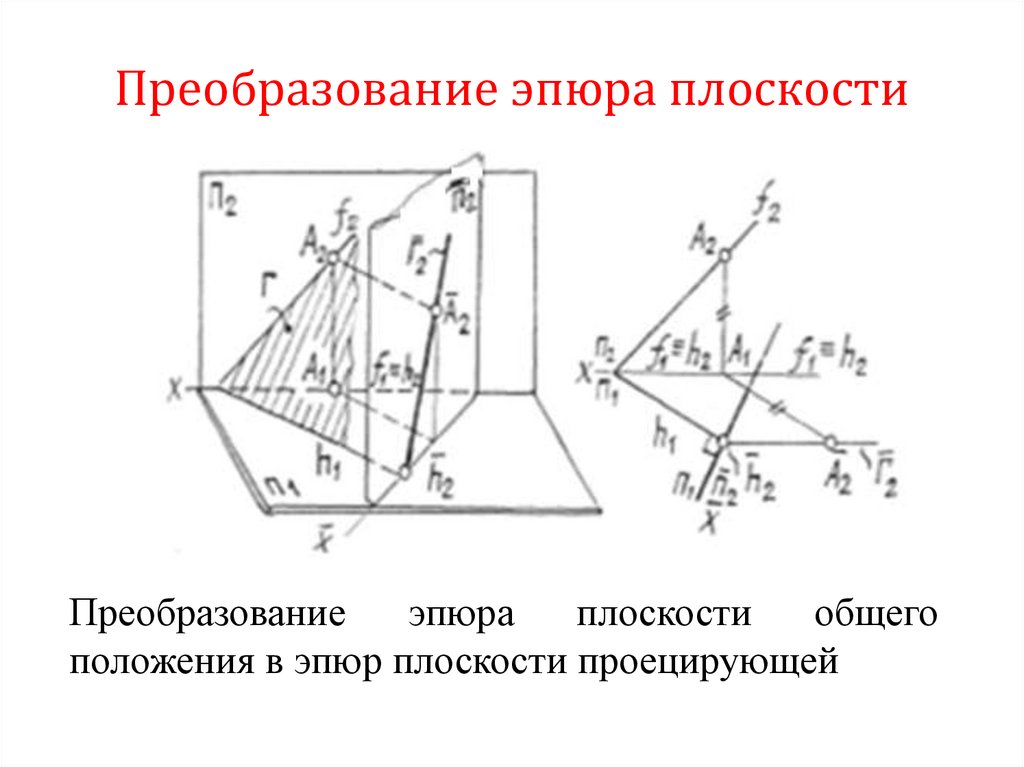
8. Преобразование эпюра плоскости

Преобразование
эпюра
плоскости
общего
положения в эпюр плоскости проецирующей

9. Преобразование плоскости общего положения, заданной треугольником АВС, в проецирующую:

А2
h2
В2
x
С2
П2
П1
А1
В1
h1
Новая ось х расположена перпендикулярно
линии уровня плоскости.
С1
П1
x
С2
П2
В2
А2

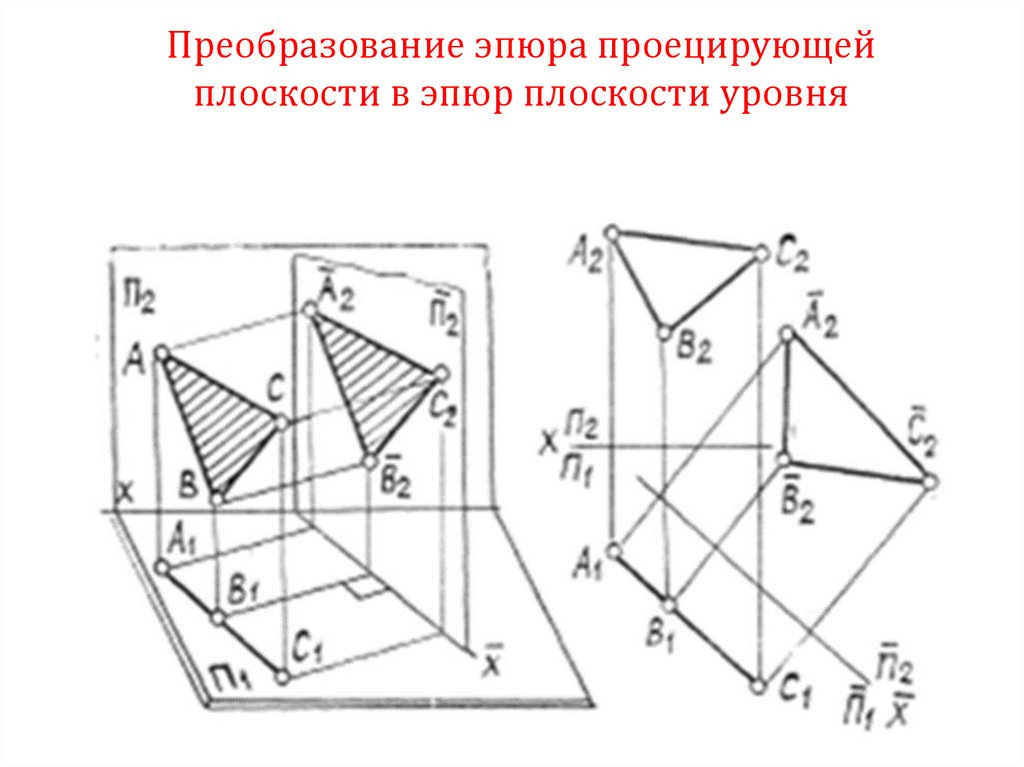
10. Преобразование эпюра проецирующей плоскости в эпюр плоскости уровня

11. Преобразование проецирующей плоскости в плоскость уровня

А2
С2
В2
х
С1
А1
Новая ось х расположена
параллельно вырожденной
проекции треугольника.
Построенная новая проекция
представляет собой
натуральную величину
В1
С2
П1
В2
А2
П2
х

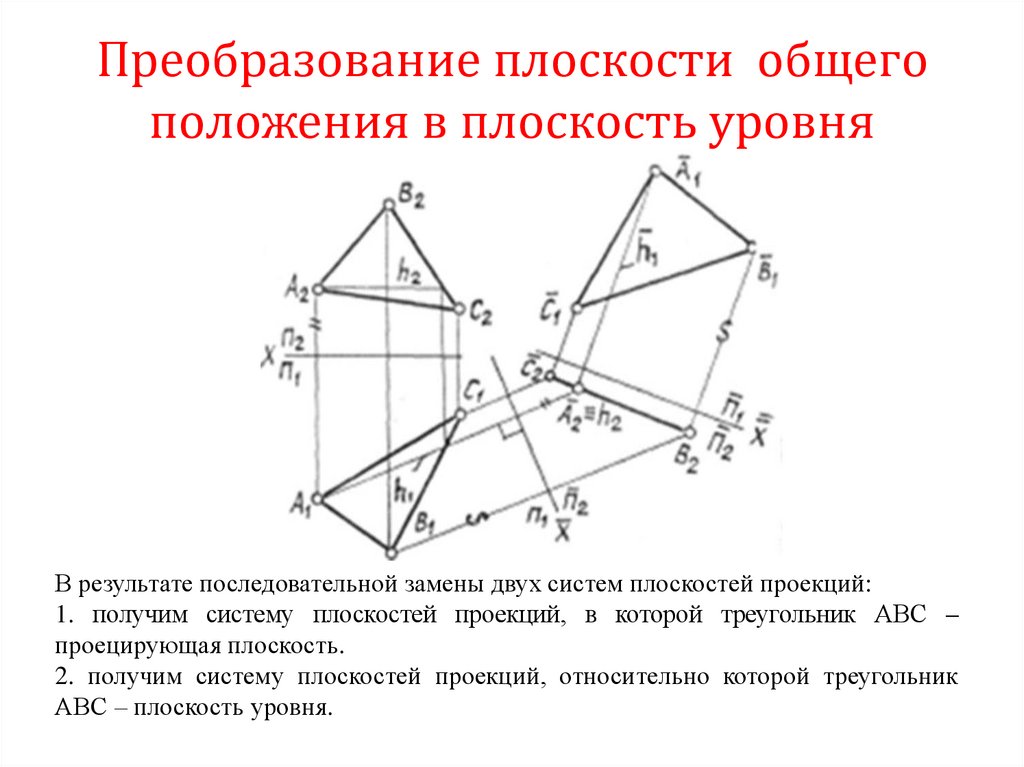
12. Преобразование плоскости общего положения в плоскость уровня

В результате последовательной замены двух систем плоскостей проекций:
1. получим систему плоскостей проекций, в которой треугольник АВС –
проецирующая плоскость.
2. получим систему плоскостей проекций, относительно которой треугольник
АВС – плоскость уровня.

13. Метрические задачи

- задачи, решение которых связано с нахождением
характеристик
геометрических
образов,
определяемых (измеряемых) линейными и
угловыми величинами.
Два вида:
А - задачи на определение расстояния между двумя
точками;
Б - задачи на нахождение величины угла между
двумя пересекающимися прямыми.

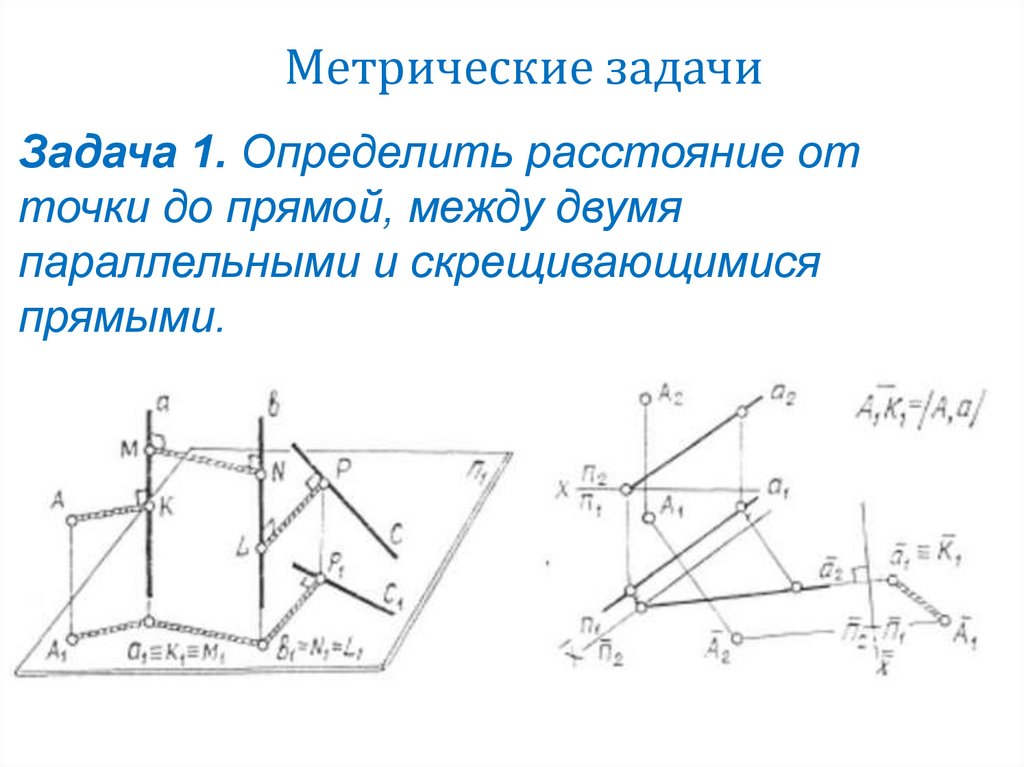
14. Метрические задачи

Задача 1. Определить расстояние от
точки до прямой, между двумя
параллельными и скрещивающимися
прямыми.

15. Определение расстояния между двумя точками способом построения прямоугольного треугольника. 

Определение расстояния между двумя точками способом
построения прямоугольного треугольника.
Длина отрезка прямой равна гипотенузе прямоугольного
треугольника, катетами которого являются разность расстояний
концов отрезка до какой-либо плоскости проекций и проекции отрезка на
эту плоскость.
Заметим, что одновременно можно определить величину угла наклона
прямой к плоскости проекций. Построения можно выполнять на
свободном поле чертежа или совмещать с любой проекцией отрезка

16. Задача 2. Определить расстояний от точки до плоскости, между параллельными плоскостями.

Задача 2. Определить расстояний от
точки до плоскости, между параллельными
плоскостями.
Расстояние от точки до плоскости - это величина перпендикуляра,
опущенного из точки на плоскость.
Если плоскость проецирующая, то искомый отрезок - линия уровня.
Если заданная плоскость занимает общее положение, следует заменить плоскость проекций так, чтобы заданная плоскость в новой
системе стала проецирующей.
Величину искомого расстояния между двумя параллельными
плоскостями можно рассматривать как длину перпендикуляра, опущенного из точки, принадлежащей одной плоскости, на другую
плоскость, т.е. решить задачу так же , как предыдущую.

17. Теорема о проецировании прямого угла

Чтобы прямой угол отображался на какой-либо плоскости
проекций без искажения, необходимо и достаточно, чтобы одна
сторона угла была параллельна плоскости проекций, а другая – не
перпендикулярна этой плоскости.
Итак, на эпюре проекцию прямого угла на П1 можно увидеть без
искажения, если одна сторона угла – горизонталь, а другая не перпендикулярна П1;
на эпюре проекцию прямого угла на П2 можно увидеть без искажения, если одна сторона угла – фронталь, а другая не пер-

18. Задача 3. Определить величину угла между пересекающимися прямыми. Известно, что любой линейный угол отобра­жается на плоскость

Задача 3. Определить величину угла между
пересекающимися прямыми.
Известно, что любой линейный угол отображается на
плоскость проекций без искажения при условии параллельности его сторон этой плоскости. Поэтому для
определения величины угла между пересекающимися
прямыми необходимо преобразовать плоскость угла в
плоскость уровня.

19. Задача 4. Определение величины двугранного угла. Двугранный угол измеряется линейным углом, составленным линиями пересечения

Задача 4. Определение величины двугранного угла.
Двугранный угол измеряется линейным углом,
составленным линиями пересечения граней двугранного
угла с плоскостью,
перпендикулярной к его ребру. Поэтому целесообразно
способом замены, плоскостей проекций преобразовать
ребро двугранного угла в проецирующую прямую, а грани в проецирующие плоскости.

20. Задача: Построить три проекции линии сечения и определить натуральную величину фигуры сечения

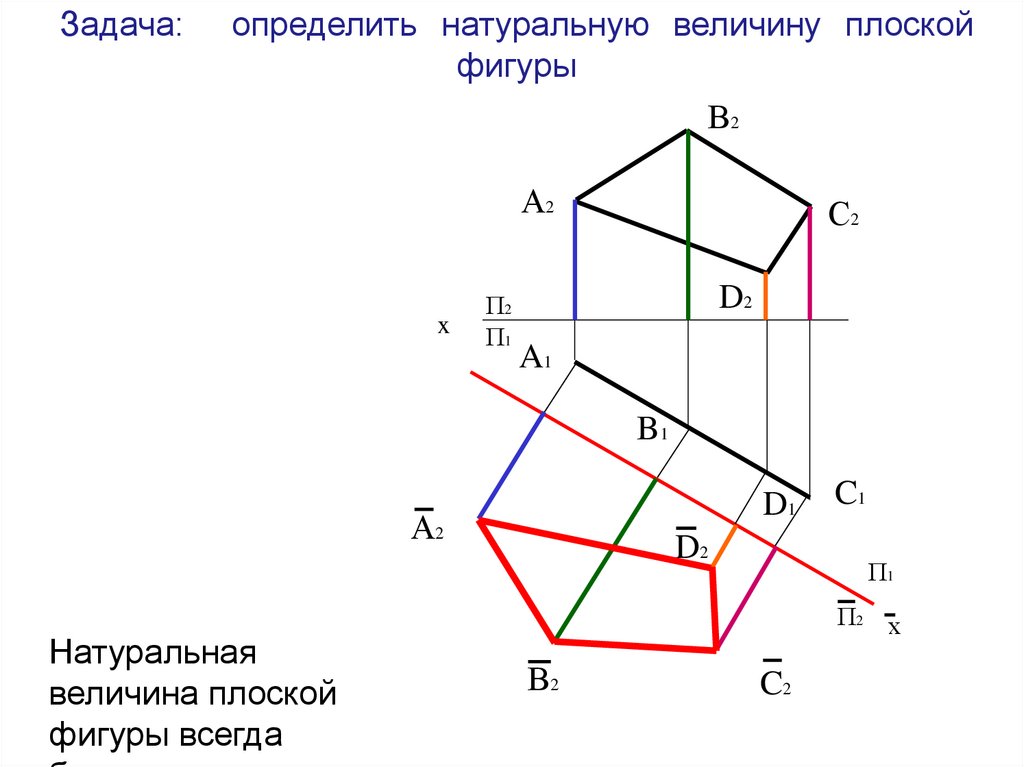
21. Задача: определить натуральную величину плоской фигуры

В2
А2
x
П2
П1
С2
D2
A1
B1
D1
А2
Натуральная
величина плоской
фигуры всегда
D2
C1
П1
П2 х
В2
C2

22. Задача : определить натуральную величину плоской фигуры

В2
h2
А2
А1
С2
п2
х п1
А1
С1
С1
С2
А2
h1
В1
В1
п1 п2
x
В2
х
Натуральная величина
геометрического образа
общего положения
больше любой
своей
проекции

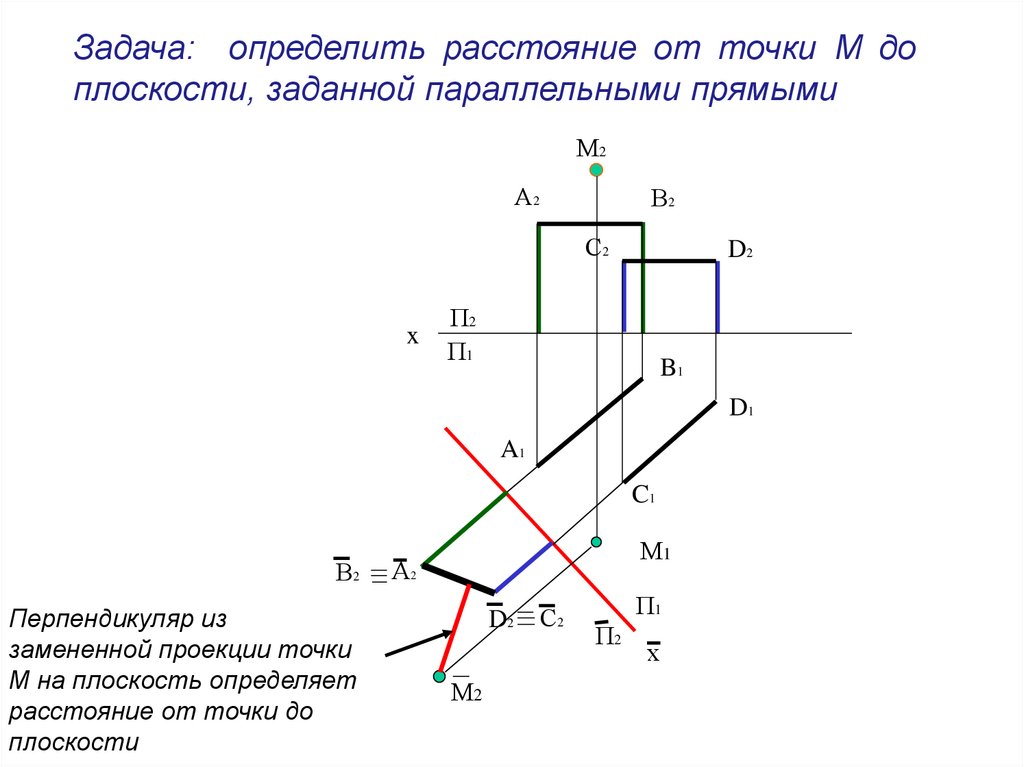
23. Задача: определить расстояние от точки М до плоскости, заданной параллельными прямыми

М2
А2
В2
С2
x
D2
П2
П1
B1
D1
A1
C1
В2
Перпендикуляр из
замененной проекции точки
М на плоскость определяет
расстояние от точки до
плоскости
М1
А2
D2
М2
С2
П1
П2
х

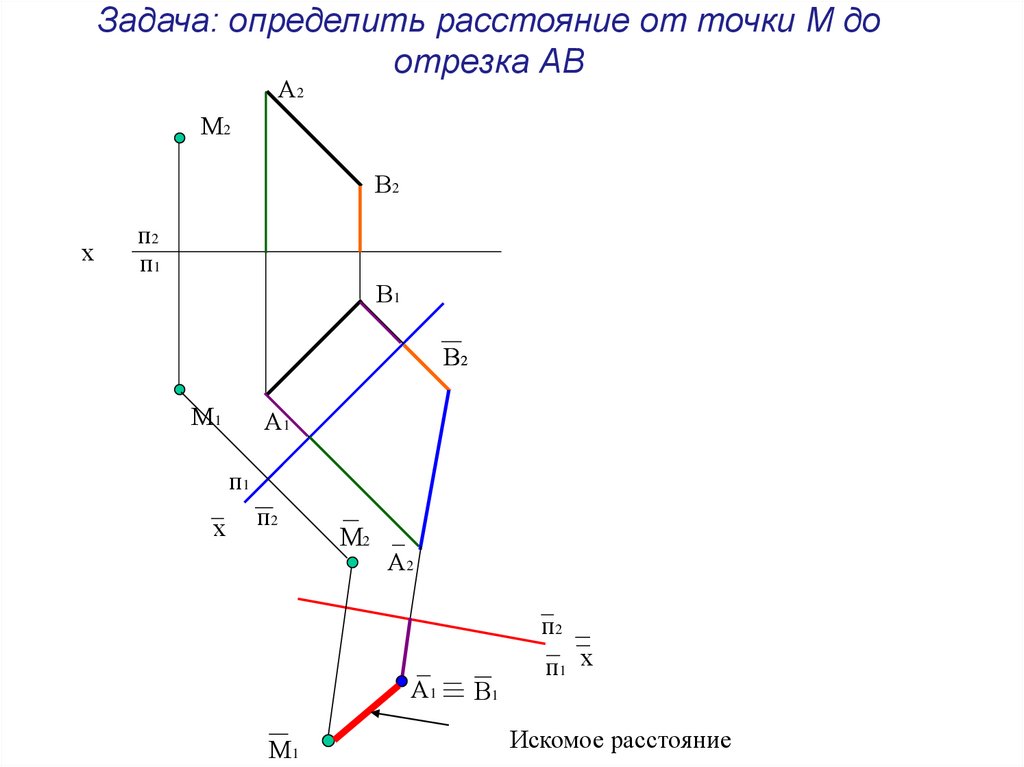
24. Задача: определить расстояние от точки М до отрезка АВ

А2
М2
В2
х
п2
п1
В1
В2
М1
А1
п1
х
п2
М2
А2
п2
А1
М1
В1
п1 х
Искомое расстояние