Метрические задачи. Способы преобразования проекций (лекция № 3)

1. Метрические задачи. Способы преобразования проекций.

ИФ МГТУ ГА
Лекция №3
Метрические задачи. Способы
преобразования проекций.
1. Метод прямоугольного треугольника
2. Определение расстояний между геометрическими объектами.
3. Определение углов между геометрическими объектами.
4. Основные принципы преобразования проекций
5. Замена плоскостей проекций;
6. Вращение вокруг проецирующей прямой
7. Вращение вокруг линии уровня
8. Плоскопараллельное перемещение

2. Метрические задачи

К метрическим задачам относятся такие, в условии или
решении которых присутствуют геометрические понятия,
связанные с численной характеристикой. Решением метрических
задач определяется перпендикулярность геометрических фигур
и численные характеристики фигур: расстояние, площадь, угол и
т. п.
•Строятся проекции расстояний и углов и определяются их
натуральные величины без преобразования плоскостей проекций
•Выполняется преобразование плоскостей проекций
геометрических фигур при котором искомые расстояния или углы
проецируются без искажения.
Далее будут рассмотрены способы построения построение
проекций искомых расстояний и углов.

3. Метод прямоугольного треугольника

Натуральная
величина отрезка
y
А2
Z=ZA-ZB
z
А2
900
m2
А
В2
x12
В2
А1
y
В
В1
m1
А1
В1
900
z
Натуральная величина
отрезка

4. Расстояние от точки до прямой

B2
12
m2
z
R2
Для определения расстояния
•Через проекции точки проводят проекции
плоскости перпендикулярной заданной
прямой;
900
22
•Находят проекции точки пересечения
прямой с плоскостью;
x 1,2
11
900
•Проекции отрезка соединяющего
проекции заданной точки и точки
пересечения являются проекциями
искомого расстояния.
R1
21
B1
y
m1
1
Расстояние от точки до прямой

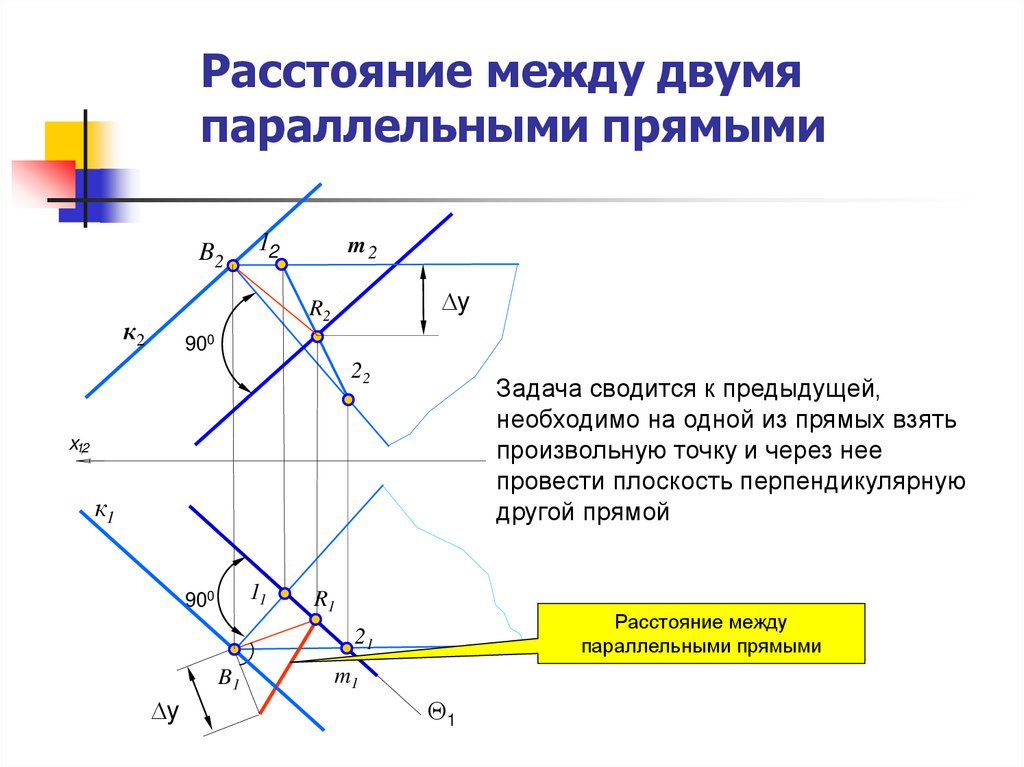
5. Расстояние между двумя параллельными прямыми

B2
12
m2
y
R2
к2
900
22
Задача сводится к предыдущей,
необходимо на одной из прямых взять
произвольную точку и через нее
провести плоскость перпендикулярную
другой прямой
x1,2
к1
11
900
R1
Расстояние между
параллельными прямыми
21
B1
y
m1
1

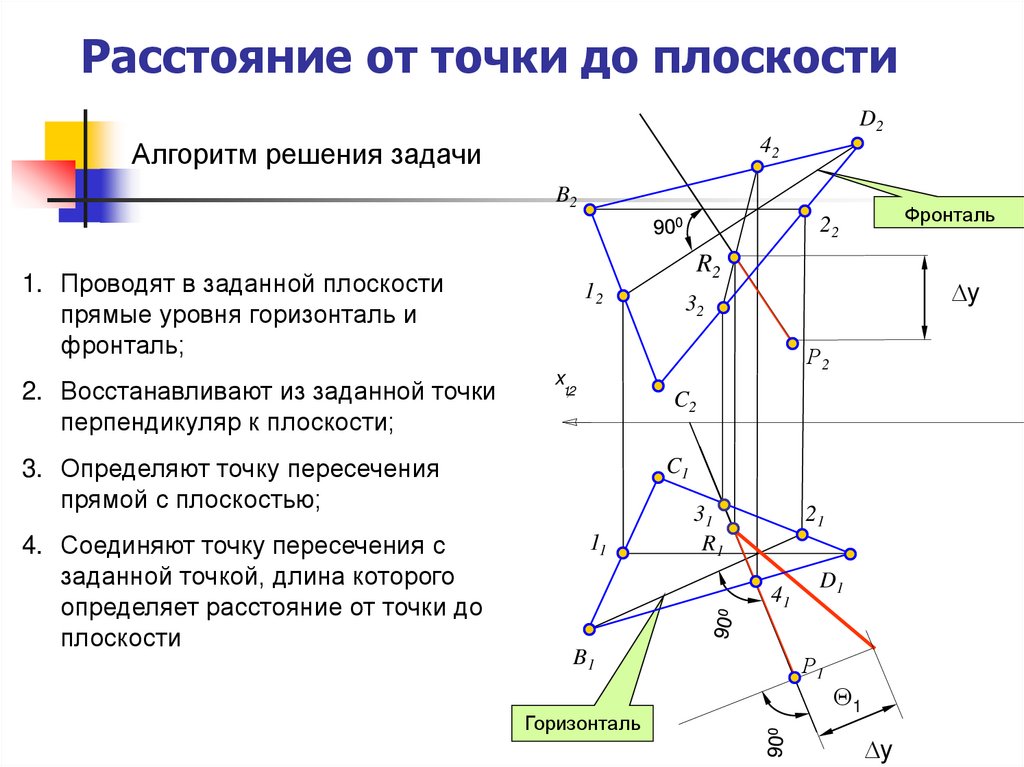
6. Расстояние от точки до плоскости

D2
42
Алгоритм решения задачи
B2
Фронталь
22
R2
1. Проводят в заданной плоскости
прямые уровня горизонталь и
фронталь;
2. Восстанавливают из заданной точки
перпендикуляр к плоскости;
12
Р2
x
1,2
C2
3. Определяют точку пересечения
прямой с плоскостью;
4. Соединяют точку пересечения с
заданной точкой, длина которого
определяет расстояние от точки до
плоскости
y
32
C1
11
21
31
R1
41
B1
Горизонталь
D1
Р1
1
y

7. Расстояние от прямой до параллельной ей плоскости

Расстояние между параллельными
плоскостями
Алгоритм решения сводится к предыдущей задачи
1. На прямой (или в плоскости) выбирают произвольную точку
2. Восстанавливают из выбранной точки перпендикуляр к
плоскости;
3. Определяют точку пересечения перпендикуляра с плоскостью;
4. Соединяют точку пересечения с точкой на прямой (в плоскости);
5. Длина полученного отрезка определяет расстояние от прямой
(плоскости) до параллельной ей плоскости

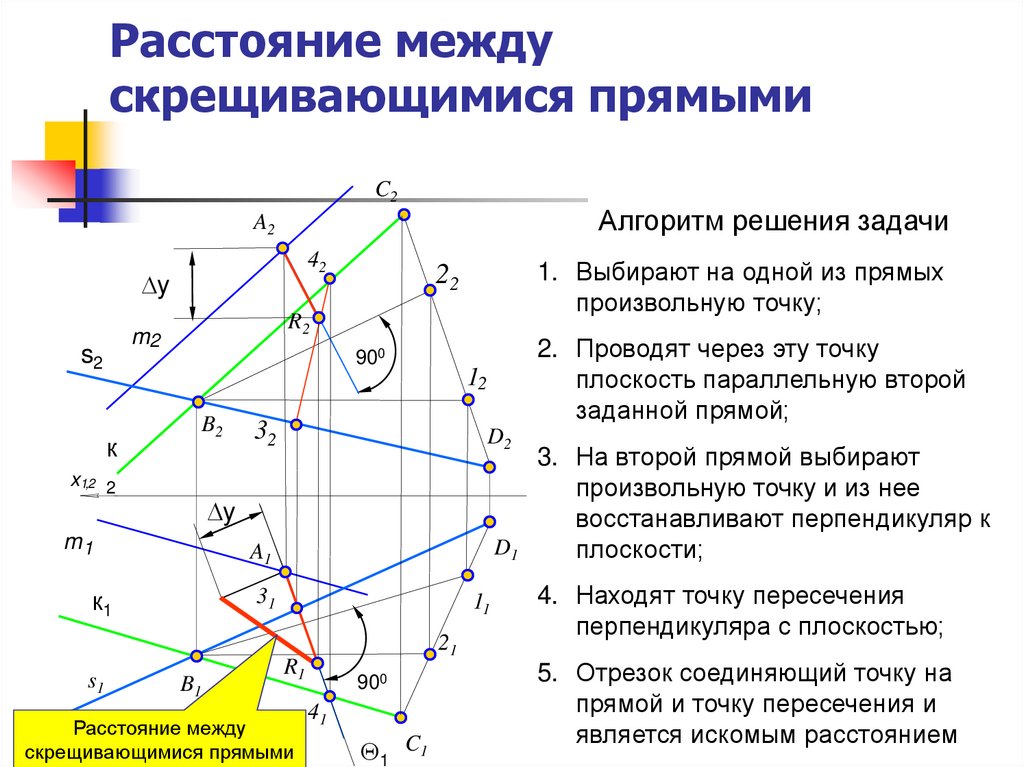
8. Расстояние между скрещивающимися прямыми

C2
Алгоритм решения задачи
A2
42
y
R2
m2
s2
к
900
B2
x1,2 2
2. Проводят через эту точку
плоскость параллельную второй
заданной прямой;
12
32
D2
A1
D1
y
m1
к1
s1
1. Выбирают на одной из прямых
произвольную точку;
22
31
B1
11
21
R1
Расстояние между
скрещивающимися прямыми
900
41
1 C1
3. На второй прямой выбирают
произвольную точку и из нее
восстанавливают перпендикуляр к
плоскости;
4. Находят точку пересечения
перпендикуляра с плоскостью;
5. Отрезок соединяющий точку на
прямой и точку пересечения и
является искомым расстоянием

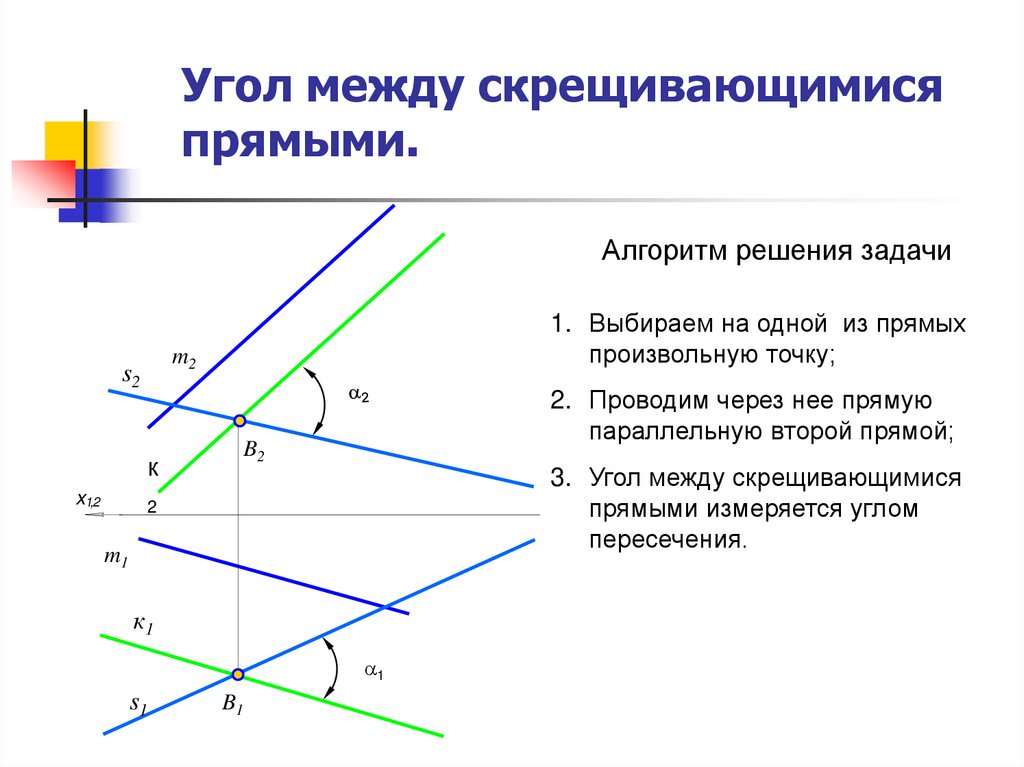
9. Угол между скрещивающимися прямыми.

Алгоритм решения задачи
m2
s2
к
x1,2
1. Выбираем на одной из прямых
произвольную точку;
2. Проводим через нее прямую
параллельную второй прямой;
B2
3. Угол между скрещивающимися
прямыми измеряется углом
пересечения.
2
m1
к1
1
s1
B1

10. Угол между прямой и плоскостью.

Угол между прямой и плоскостью измеряется углом между
прямой и ее прямоугольной проекцией на данную плоскость.
D2
А
1
B2
В
22
12
m2
С
Алгоритм решения задачи
Р2
C2
x1,2
C1
1. Выбирают произвольную точку на
прямой;
2. Из точки восстанавливают
перпендикуляр к плоскости;
3. Угол пересечения заданной прямой
и перпендикуляра дополняет
искомый угол до прямого угла
Фронталь
21
11
D1
Р1
B1
Горизонталь
m1

11. Угол между двумя плоскостями.

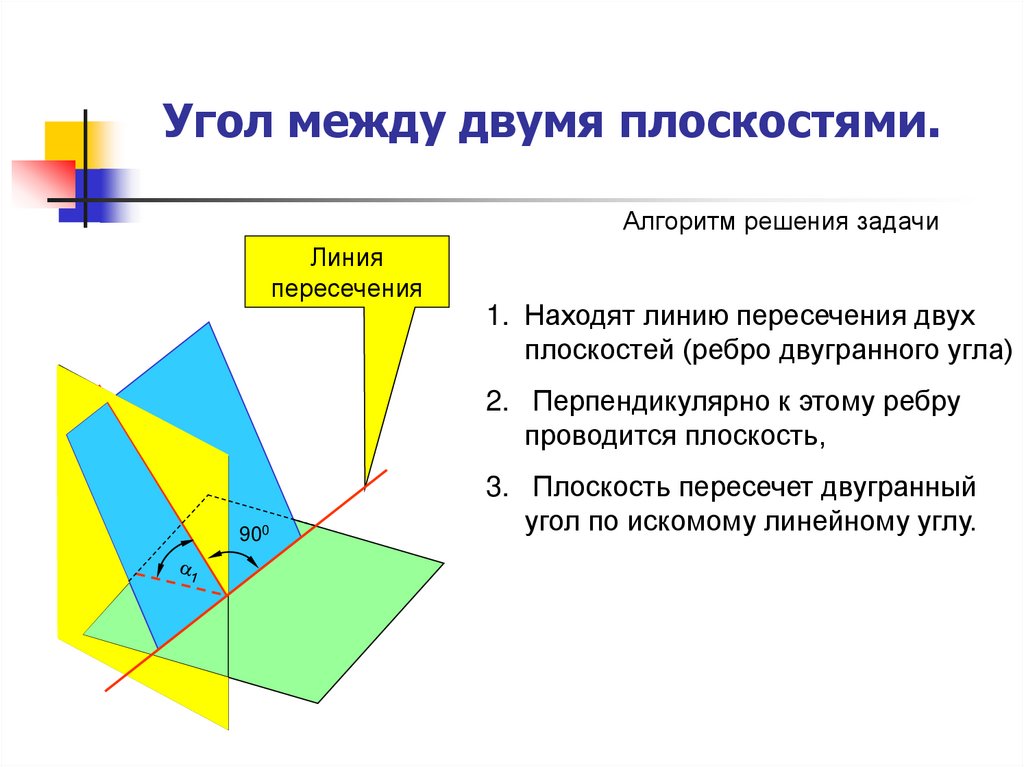
Алгоритм решения задачи
Линия
пересечения
1. Находят линию пересечения двух
плоскостей (ребро двугранного угла)
2. Перпендикулярно к этому ребру
проводится плоскость,
900
3. Плоскость пересечет двугранный
угол по искомому линейному углу.

12. Угол между двумя плоскостями.

D2
N2
B2
M2
22
32
12
2
Угол между плоскостями
равен углу между
перпендикулярами к ним,
проведенными из точки
находящейся вне
двугранного угла.
42
C2
A2
K2
C1
K1
21
11
31
41
D1
N1
B1
1
M1
A1

13. Основные принципы преобразования проекций

Методы преобразования основываются на двух принципах:
• изменение взаимного положения объекта и плоскостей проекций;
• изменение направления проецирования.
Первый принцип реализуют способ замены плоскостей проекций,
метод плоскопараллельного перемещения и методы вращения
вокруг различных осей (вращения относительно фронтальной или
горизонтальной проецирующей линии, вращение относительно
прямой уровня и т. д.)
Второй принцип основывается на изменении направления
проецирования относительно неизменных плоскостей проекций
(косоугольное вспомогательное проецирование), используется
преимущественно для решения позиционных задач

14. Замена плоскостей проекций

А2
П2
zA
В2
zA
zB
zB
А1
П1

15. Определение натуральной величины отрезка на комплексном чертеже

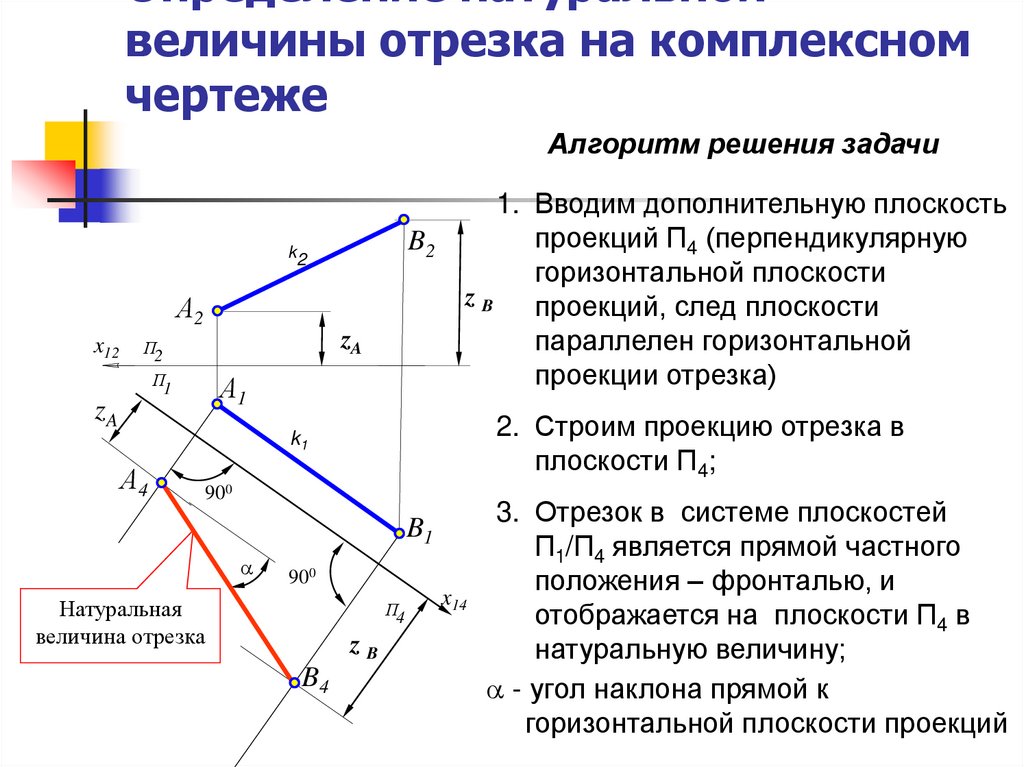
Алгоритм решения задачи
B2
k2
А2
x12
zA
П2
П1
А1
zA
2. Строим проекцию отрезка в
плоскости П4;
k1
А4
900
B1
900
Натуральная
величина отрезка
П4
zB
B4
1. Вводим дополнительную плоскость
проекций П4 (перпендикулярную
горизонтальной плоскости
zB
проекций, след плоскости
параллелен горизонтальной
проекции отрезка)
3. Отрезок в системе плоскостей
П1/П4 является прямой частного
положения – фронталью, и
x14
отображается на плоскости П4 в
натуральную величину;
- угол наклона прямой к
горизонтальной плоскости проекций

16. Замена плоскостей проекций

Натуральная
величина
треугольника
П2
горизонталь
А2
А
А
С2
В2
С
А4
В
В
С
В2
А1
С4
В4
900
С2
П1
П5

17. Определение натуральной величины треугольника на комплексном чертеже

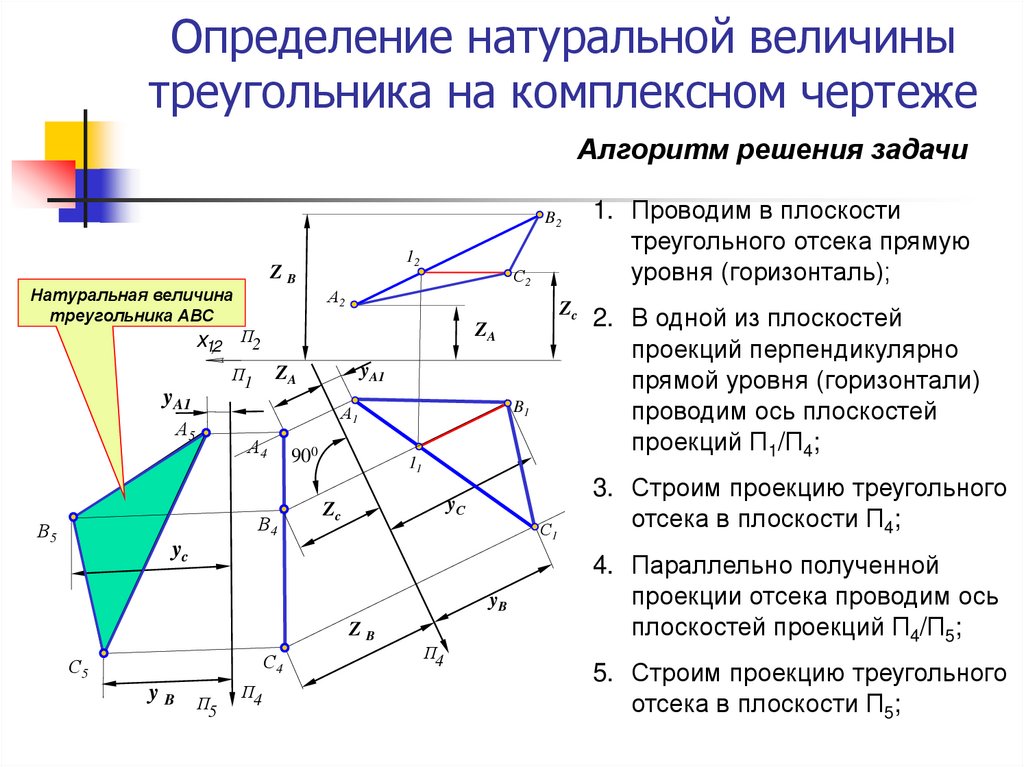
Алгоритм решения задачи
B2
Натуральная величина
треугольника АВС
x1,2
yA1
ZA
А4
В4
B1
900
11
yС
Zc
С1
yc
yB
ZB
С4
С5
yB
П5
П4
Zc
ZA
П2
А1
А5
В5
С2
А2
П1
yA1
12
ZB
П4
1. Проводим в плоскости
треугольного отсека прямую
уровня (горизонталь);
2. В одной из плоскостей
проекций перпендикулярно
прямой уровня (горизонтали)
проводим ось плоскостей
проекций П1/П4;
3. Строим проекцию треугольного
отсека в плоскости П4;
4. Параллельно полученной
проекции отсека проводим ось
плоскостей проекций П4/П5;
5. Строим проекцию треугольного
отсека в плоскости П5;

18. Вращение вокруг проецирующей прямой

В2
П2
А2
В
В21
А1
R
Проецирующая прямая
В1
В11
П1

19.

Вращение вокруг проецирующей
прямой на комплексном чертеже
Алгоритм решения задачи
B2
k2
1. Проводим через произвольную точку
отрезка проецирующую прямую;
А2
2. Поворачиваем проекцию отрезка
относительно точки так, что бы
отрезок принял частное положение
относительно плоскостей проекций
(стал прямой уровня);
x1,2
А1
k1
B1 3.
B1
Натуральная величина
отрезка АВ
Вторая точка при повороте отрезка
относительно проецирующей прямой
совершает перемещение в плоскости
перпендикулярной проецирующей
прямой (проекция точки движется
параллельно оси эпюра)

20.

Вращение вокруг прямой уровня
Пусть требуется определить угол между двумя пересекающимися
прямыми.
k2
F2
D2
x1,2
E2
С2
А2
А1
E1
F1
B1
z
z
2. Проводим через точку прямую уровня;
3. Опускаем из вершины треугольника
перпендикуляр на прямую уровня;
m1
C1
k1
1. Выбираем произвольную точку ;
m2
900
D1
Алгоритм решения задачи
B2
4. Методом прямоугольного треугольника
определяем натуральную величину
перпендикуляра;
5. Строим натуральную величину угла
пересечения двух прямых.

21.

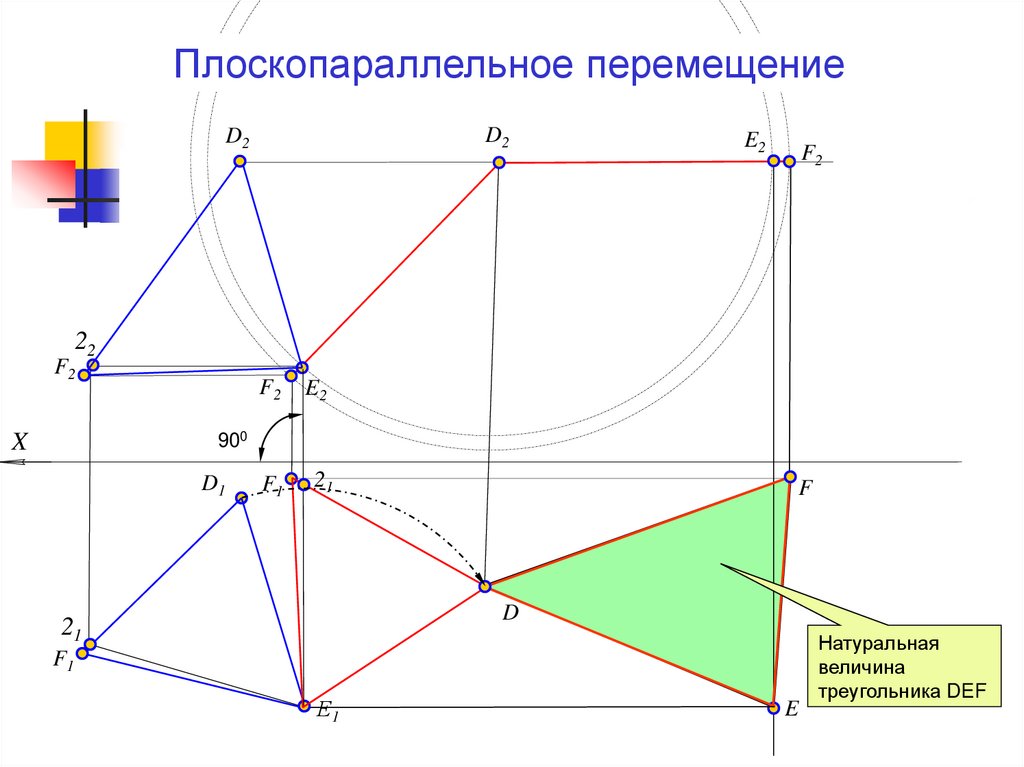
Плоскопараллельное перемещение
D2
D2
E2
F2
22
F2
F2
E2
F1
21
900
X
D1
F
D
21
F1
Е1
E
Натуральная
величина
треугольника DEF