Числовые характеристики дискретных случайных величин

1.

Числовые характеристики
дискретных случайных
величин

2.

Устная работа.
А) Какая из таблиц не задает закон
распределения случайной величины?
Объясните почему.
x
p
0
1
2
3
0,1 0,5 0,1 0,3
x
p
1
2
3
4
0,3 0,1 0,3 0,2
x
p
–1 1
2
3
0,1 0,2 0,3 0,4

3.

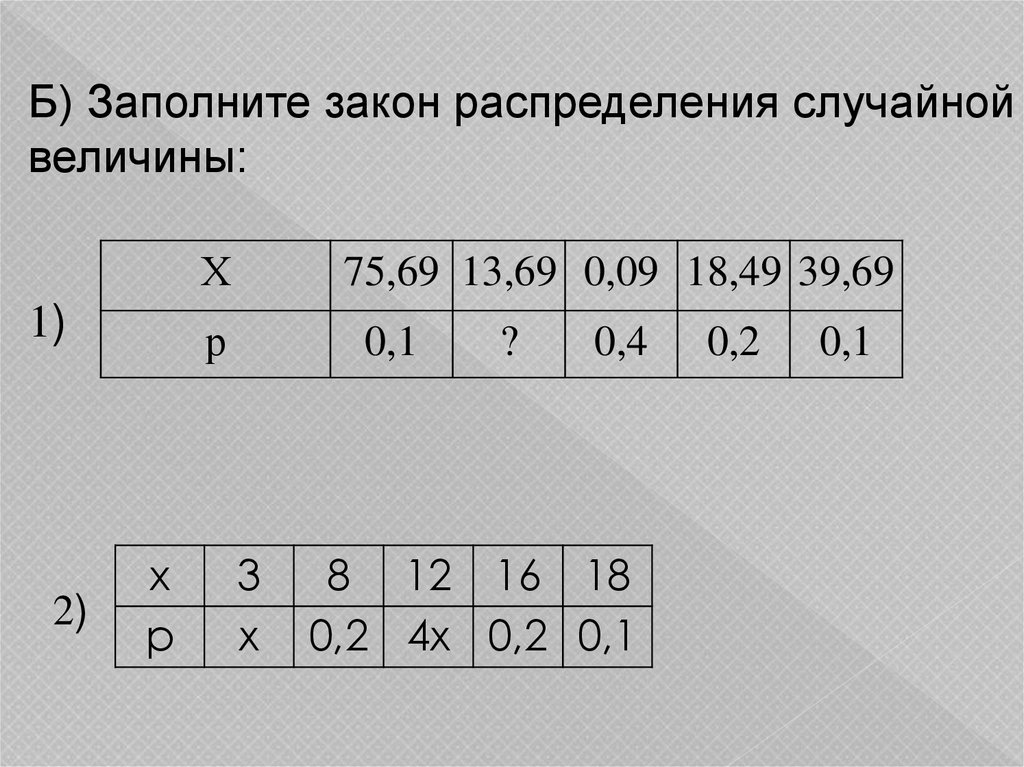
Б) Заполните закон распределения случайной
величины:
1)
2)
х
р
Х
75,69 13,69 0,09 18,49 39,69
р
0,1
3
х
?
0,4
8 12 16 18
0,2 4х 0,2 0,1
0,2
0,1

4.

Математическое ожидание — это среднее значение случайной
величины.
Считается так: сумма всех значений случайной величины,
умноженных на вероятности их появления.
Математическим ожиданием дискретной случайной величины Х,
представляющей собой ряд чисел х1, х2, х3, …, с распределением
вероятностей их появления соответственно р1, р2, р3, …
называется величина которая рассчитывается следующим
образом:
M(X) = х1*р1 + х2*р2 + х3*р3 + …

5.

Постоянную С можно рассматривать как
дискретную случайную величину,
принимающую лишь одно значение С с
вероятностью р = 1. Поэтому M(С) = С

6.

2. Постоянный множитель можно
выносить за знак математического
ожидания, т. е. М(СХ) = С М(Х).
Используя соотношение имеем
М(СХ) =C х1р1+Cх2р2 + ... +Cхn р n.=
С(х1р1+х2р2 + ... +хn р n.) = СМ(Х).

7.

3. Математическое ожидание суммы
двух случайных величин X и Y
равно сумме их математических
ожиданий:
М(Х +Y) = М(Х) + М(Y).
Определение. Случайные величины
X и Y называют независимыми, если закон
распределения каждой из них не зависит
от того, какое возможное значение
приняла другая величина.

8.

4. Математическое ожидание
Произведения двух
независимых случайных
величин равно произведению
их математических ожиданий:
М(Х Y) = М(Х)×М(Y).

9.

5. Математическое ожидание
разности двух случайных
величин X и Y равно разности
их математических ожиданий:
М(Х -Y) = М(Х) - М(Y).

10.

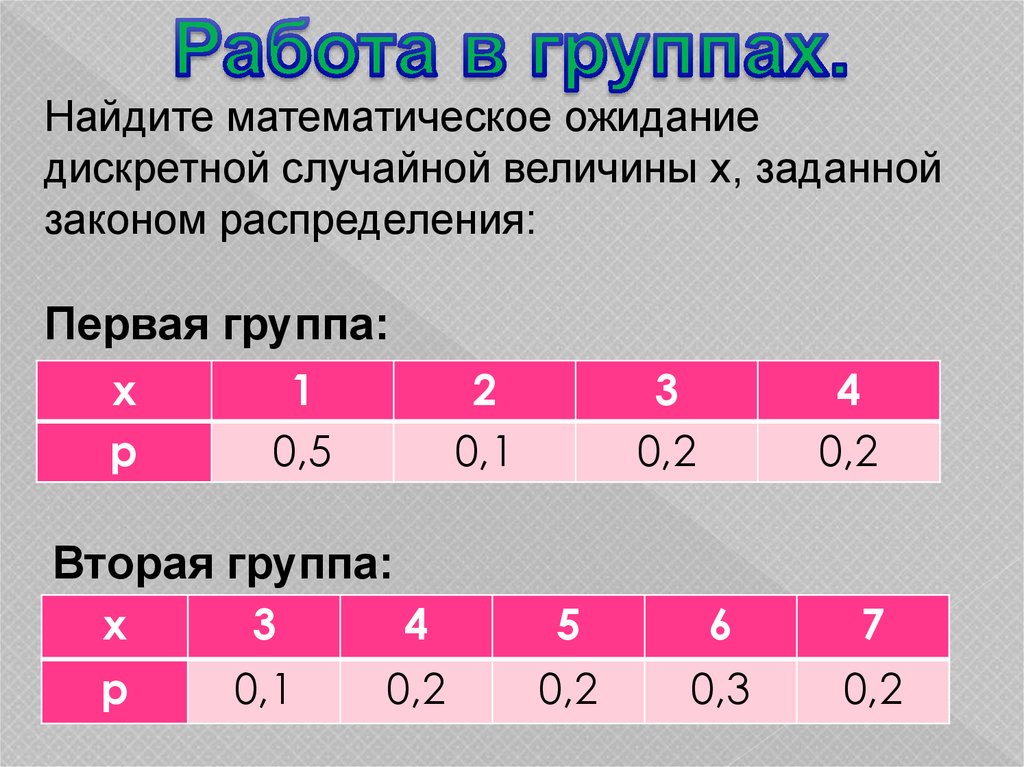
Найдите математическое ожидание
дискретной случайной величины х, заданной
законом распределения:
Первая группа:
х
р
1
0,5
2
0,1
3
0,2
4
0,2
Вторая группа:
х
р
3
0,1
4
0,2
5
0,2
6
0,3
7
0,2

11.

Первая группа:
1) М(Х) = 1 · 0,5 + 2 · 0,1 + 3 · 0,2 + 4 · 0,2 =
0,5 + 0,2 + 0,6 + 0,8 = 2,1
Вторая группа:
2) М(Х) = 3 · 0,1 + 4 · 0,2 + 5 · 0,2 + 6 · 0,3 +
7 · 0,2 = 0,3 + 0,8 + 1 + 1,8 + 1,4 = 2,1 = 7,4

12.

Задача 1.
Найдите математическое ожидание случайной
величины Z = X + 2 Y, если известны
математические ожидания случайных
величин Х и Y: М(Х) = 5, М(Y) = 3.
Задача 2.
Независимые случайные величины заданы
законами распределения
Х
Р
1 2
0,2 0,8
Х
Р
0,5 1
0,3 0,7
Найти математическое ожидание случайной
величины ХY

13.

Задача 1.
Используя свойства 3 и 2 математического
ожидания, получаем
М(Z) = М(Х + 2Y) = М(Х) + М(2Y) = М(Х) + 2М(Y) =5 +
2×3 = 11.
Задача 2.
Найдем математические ожидания каждой из
данных величин:
М(Х) = 1· 0,2 + 2 · 0,8 = 1,8,
М(Y) = 0,5 · 0,3 + 1 · 0,7 = 0,15 + 0,7 = 0,85.
Случайные величины Х и Y независи-мы, поэтому
искомое математическое ожидание
М(ХY) = М(Х)×М(Y) = 1,8 · 0,85 = 1,53.
Ответ: М(ХY) = 1,53

14.

Независимые случайные величины заданы
законами распределения
Х
Р
1
2
3
0,7 0,1 0,2
Y
1
1
2
Р
0,4 0,2 0,5
Найти математическое ожидание случайной
величины 2Х + 3Y

15.

1) М(х) = 1 ∙ 0,7 + 2 ∙ 0,1 + 3 ∙ 0,2 = 0,7 + 0,2 +
0,6 = 1,5.
2) М(у) = 1 ∙ 0,4 + 1 ∙ 0,2 + 2 ∙ 0,5 = 0,4 + 0,2 +
1 = 1,6.
М(2Х + 3 Y) = 2 · 1,5 + 3 · 1,6 = 3 + 4,8 = 7,8
Ответ: М(2Х + 3 Y) = 7,8

16.

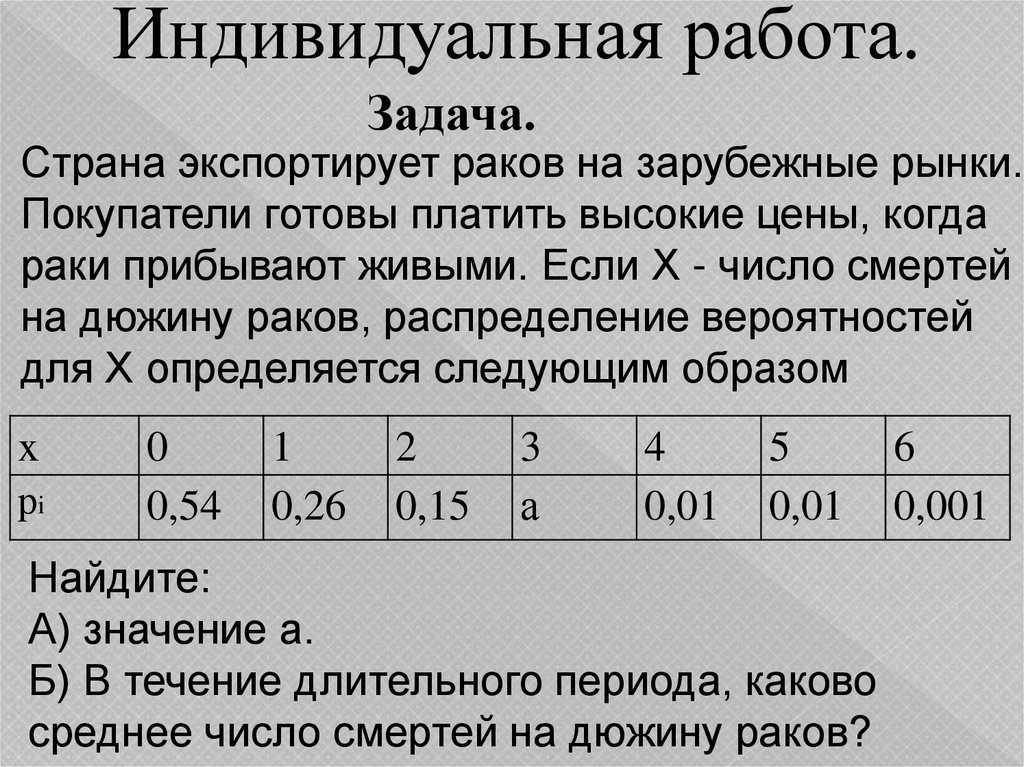
Индивидуальная работа.
Задача.
Страна экспортирует раков на зарубежные рынки.
Покупатели готовы платить высокие цены, когда
раки прибывают живыми. Если X - число смертей
на дюжину раков, распределение вероятностей
для X определяется следующим образом
x
рi
0
0,54
1
0,26
2
0,15
3
а
4
0,01
5
0,01
Найдите:
А) значение а.
Б) В течение длительного периода, каково
среднее число смертей на дюжину раков?
6
0,001

17.

Решение:
а = 1 – (0,54 + 0,26 + 0,15 + 0,01+ 0,01 + 0,01 =
0,02
М(Х) = 0 · 0,54 + 1 · 0,26 + 2·0,15 + 3 · 0,02 + 4 ·
0,01 + 5 · 0,01 + 6 · 0,01 = 0 + 0,26 + 0,06 + 0,04 +
0,05 + 0,06 = 0,47
Ответ: А) 0,02;
Б) 0,47.

18.

Известны математические ожидания случайных величин:
Найдите

19. Определение дисперсии

ДИСПЕРСИЕЙ (от латинского слова dispersion-рассеяние) и
обозначается буквой D или