Похожие презентации:
Приложения двойного интеграла. Вычисление объемов тел
1.
Изгеометрического
смысла
двойного
интеграла следует, что любой двойной
интеграл задает объем тела, ограниченного
сверху графиком подынтегральной функции,
снизу – областью D, с боков – цилиндрической
поверхностью с направляющими по границе
области D.
2.
Вычислить объем тела,ограниченного поверхностями
z x y,
x y a, (a 0)
z 0
3.
Посколькуподынтегральная
функция
должна быть не отрицательна, то область
интегрирования ограничена на плоскости
ХОУ
прямоугольным
равнобедренным
треугольником с катетами, равными а.
y
a
D
0
a
x
4.
a xa
a
1
2 a x
D x y dxdy 0 dx 0 x ydy 2 0 dx x y 0
a
a
1
1
2
dx x (a x) dx ( x 3 2a x 2 a 2 x)
20
20
1 x
2ax
a x
2 4
3
2
4
3
2
2
a
a4
(куб .ед.)
0 24
5.
Площадь некоторой области D может бытьнайдена по формуле:
dxdy S
D
D
6.
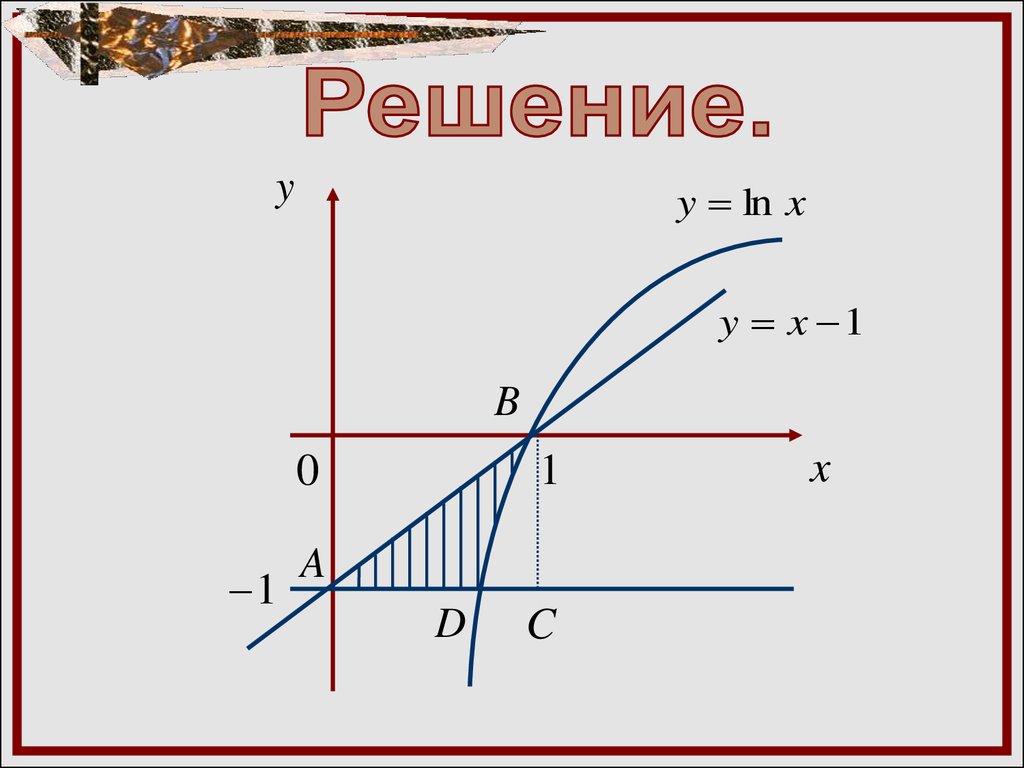
Вычислить площадь фигуры,ограниченной линиями:
y ln x,
x y 1,
y 1
7.
yy ln x
y x 1
B
1
0
1
A
D
C
x
8.
S ABD S ABC S BCDS ABC -площадь прямоугольного треугольника,
катеты которого равны 1.
S ABC
1
2
S BCD -ограничена снизу прямой y=-1 при
1
x 1
e
-сверху кривой y=lnx и справа прямой
x=1.
9.
1S ABD
ln x
1
1
dxdy dx dy
2 BCD
2 1
1
e
1
1
1
1
ln x
dx y 1 dx ln x 1
2 1
2 1
e
e
ln x 1 u
1
du dx
x
dx dv
x v
10.
11
x ln x 1
e
2
1
1
1 1
1
1 x x dx 2 e e x 1e
e
1
1 1 1
1 1 кв.ед.
2
e 2 e








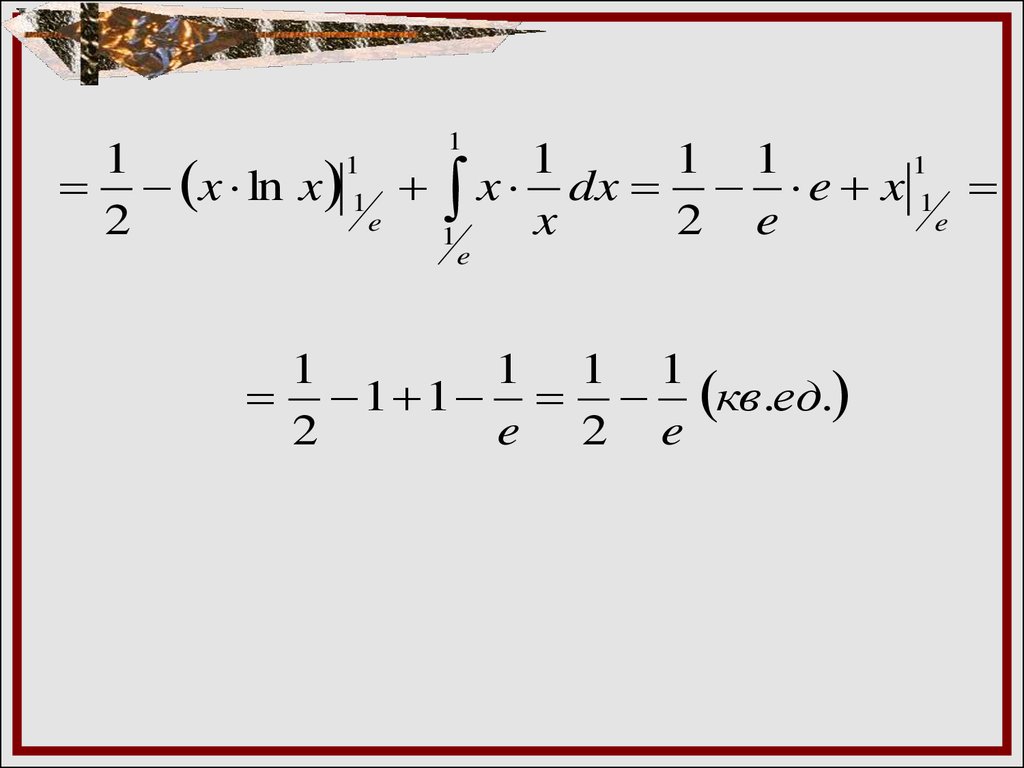
 Математика
Математика








