Векторы (понятие вектора, сложение и вычитание векторов, умножение вектора на число)

1. Векторы (понятие вектора, сложение и вычитание векторов, умножение вектора на число)

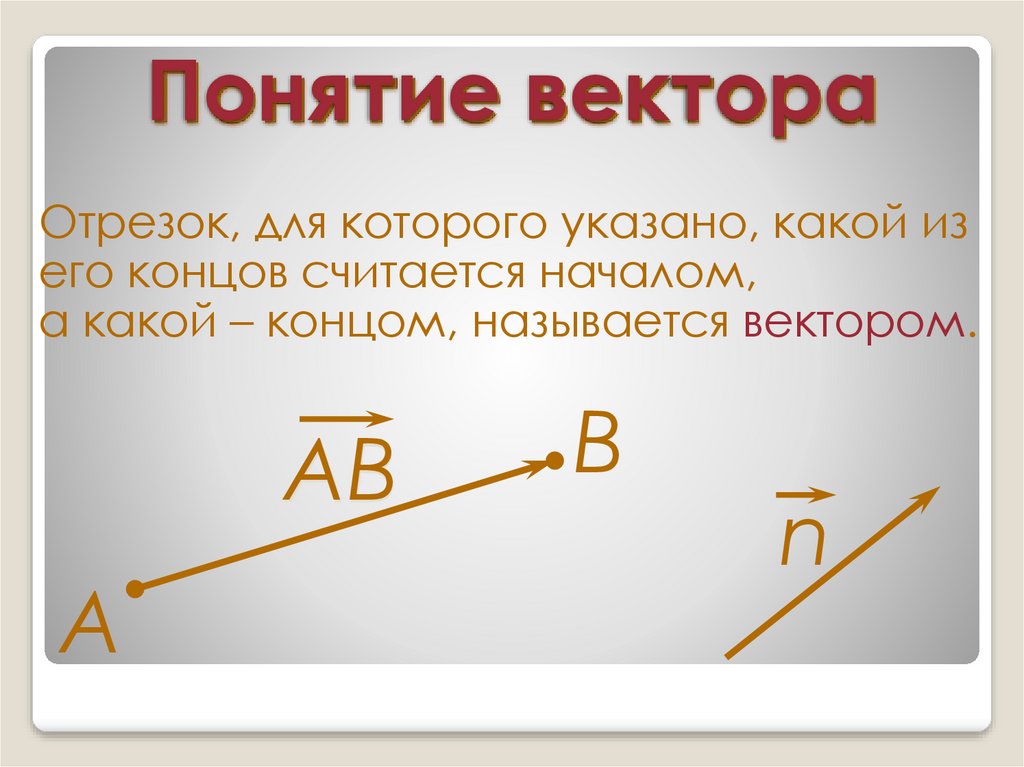
2. Понятие вектора

Отрезок, для которого указано, какой из
его концов считается началом,
а какой – концом, называется вектором.
АВ
А
В
n

3. Нулевой вектор

Любая точка на плоскости может
рассматриваться как вектор.
Такой вектор называется нулевым.
М
ММ = 0

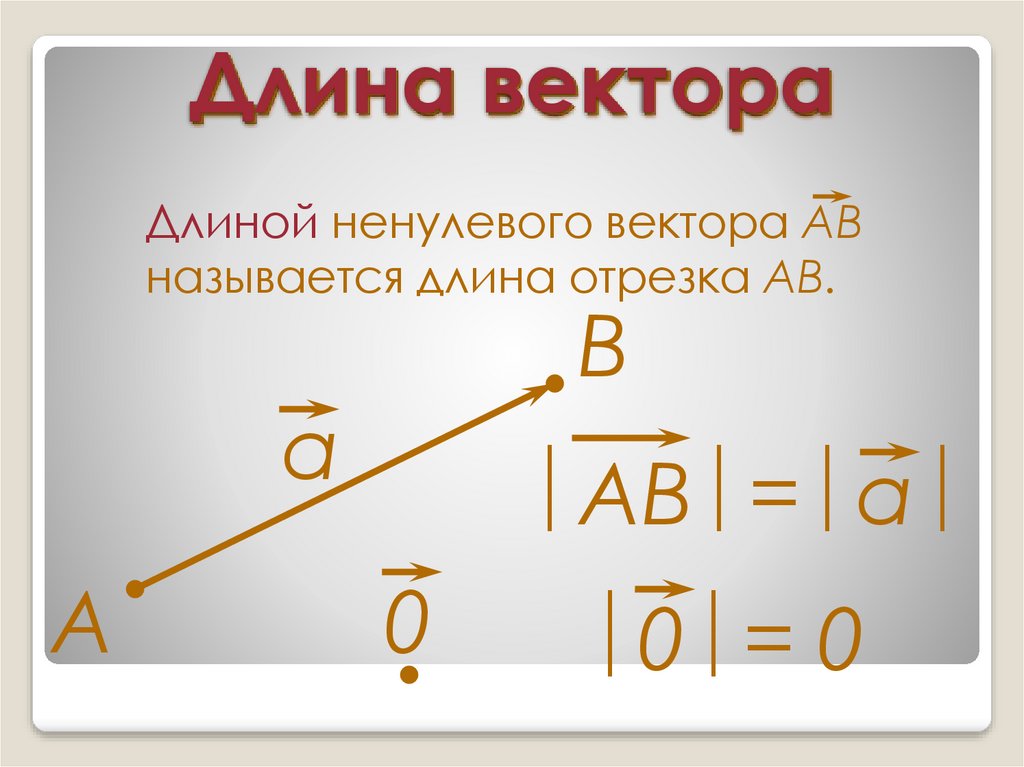
4. Длина вектора

Длиной ненулевого вектора АВ
называется длина отрезка АВ.
В
а
А
АВ = а
0
0 = 0

5. Коллинеарность векторов

Два ненулевых вектора называются
коллинеарными, если они лежат на одной
прямой или на параллельных прямых.
q
р
r

6. Сонаправленные векторы

Два коллинеарных вектора
называются сонаправленными,
если у них совпадают направления.
q
р
q↑↑р

7. Противоположно направленные векторы

Два коллинеарных вектора называются
противоположно направленными, если
они не сонаправлены.
а
b
a↑↓b

8. Равные векторы

Векторы называются равными, если
они сонаправлены и их длины равны.
q
р
q↑↑р
q = р
q=р

9. Откладывание вектора от данной точки

От любой точки М можно отложить
вектор, равный данному вектору а,
и притом только один.
А
a
М
В
N

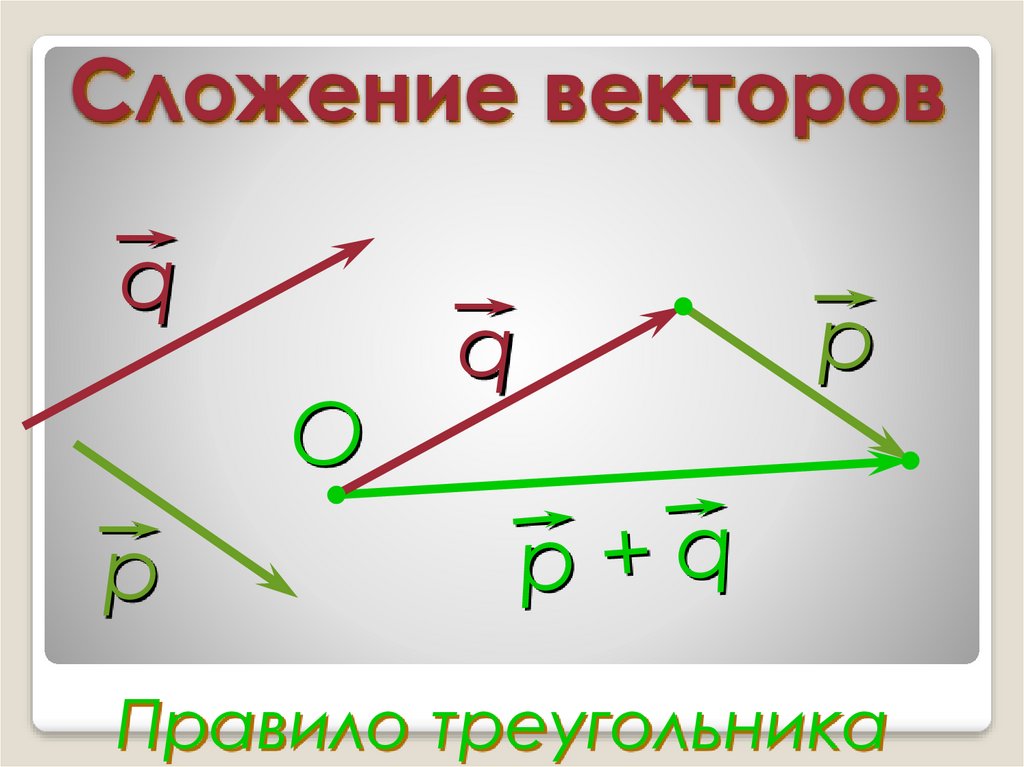
10. Сложение векторов

q
O
q
р
р
Правило треугольника

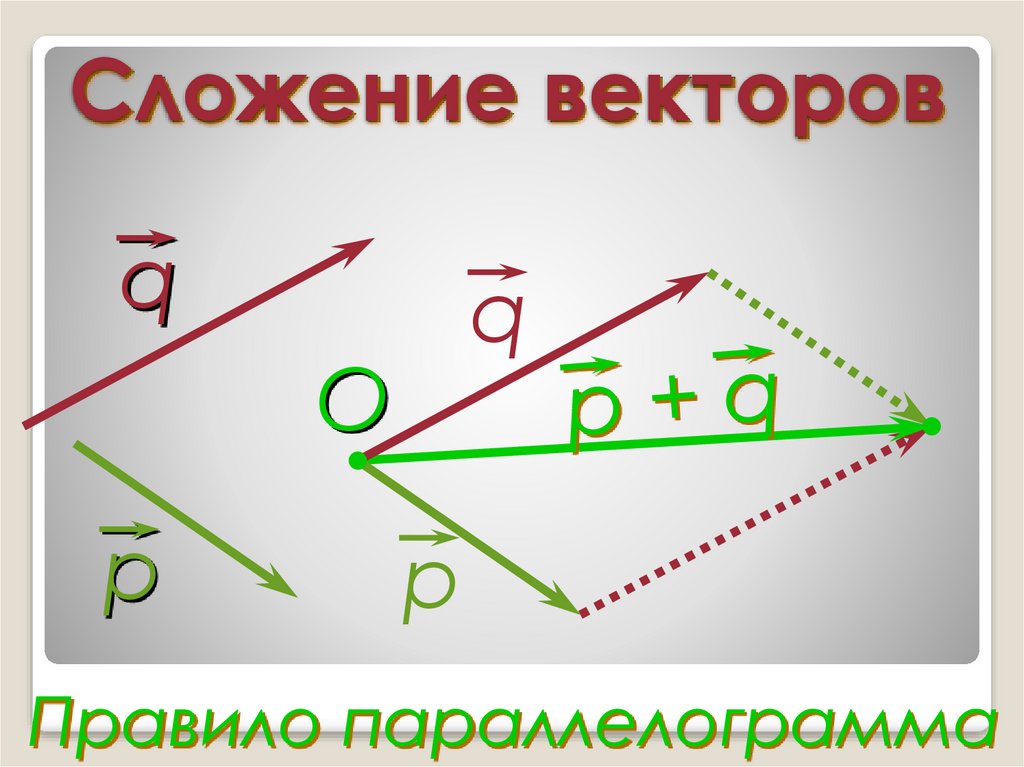
11. Сложение векторов

q
q
O
р
р
Правило параллелограмма

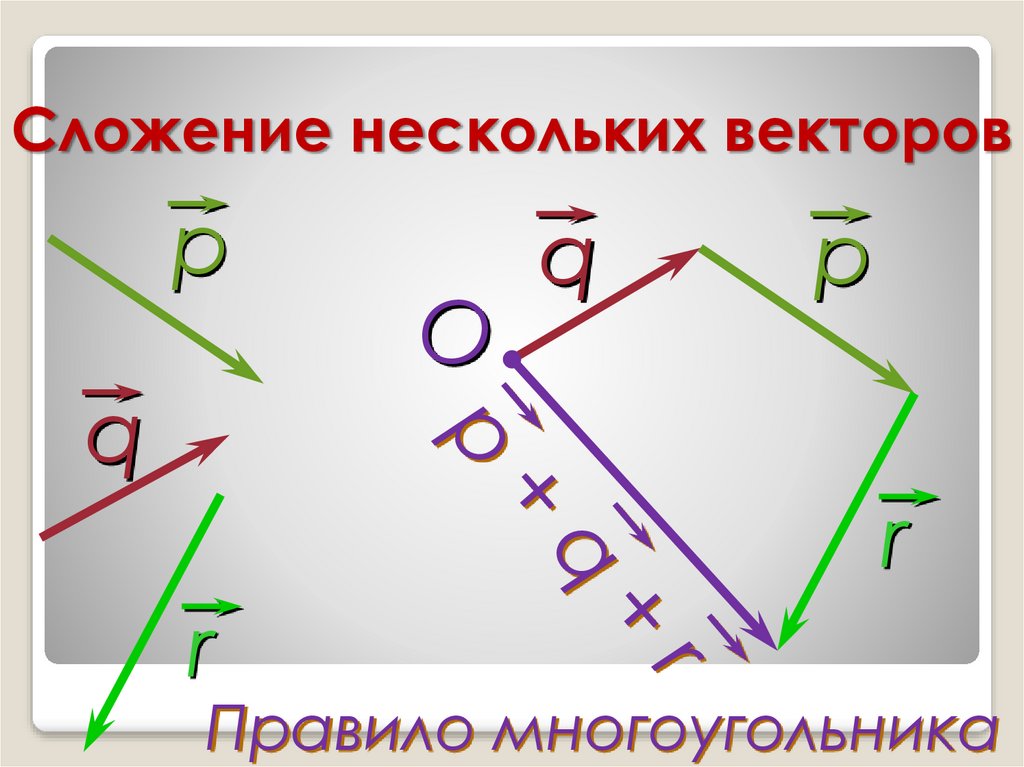
12. Сложение нескольких векторов

р
q
O
q
р
r
r
Правило многоугольника

13. Свойства сложения

а + b= b + a
− переместительный закон
(а + b) + с = (b + с) + a
− сочетательный закон
а − b = a +(− b)
− разность векторов

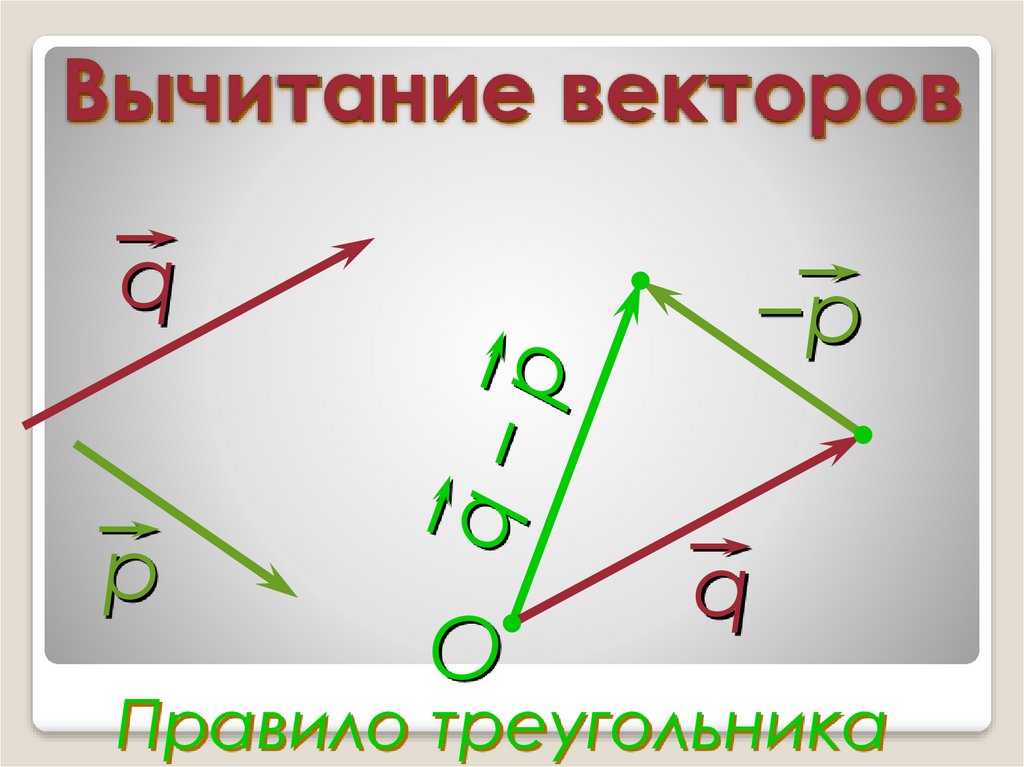
14. Вычитание векторов

q
р
−р
O
q
Правило треугольника

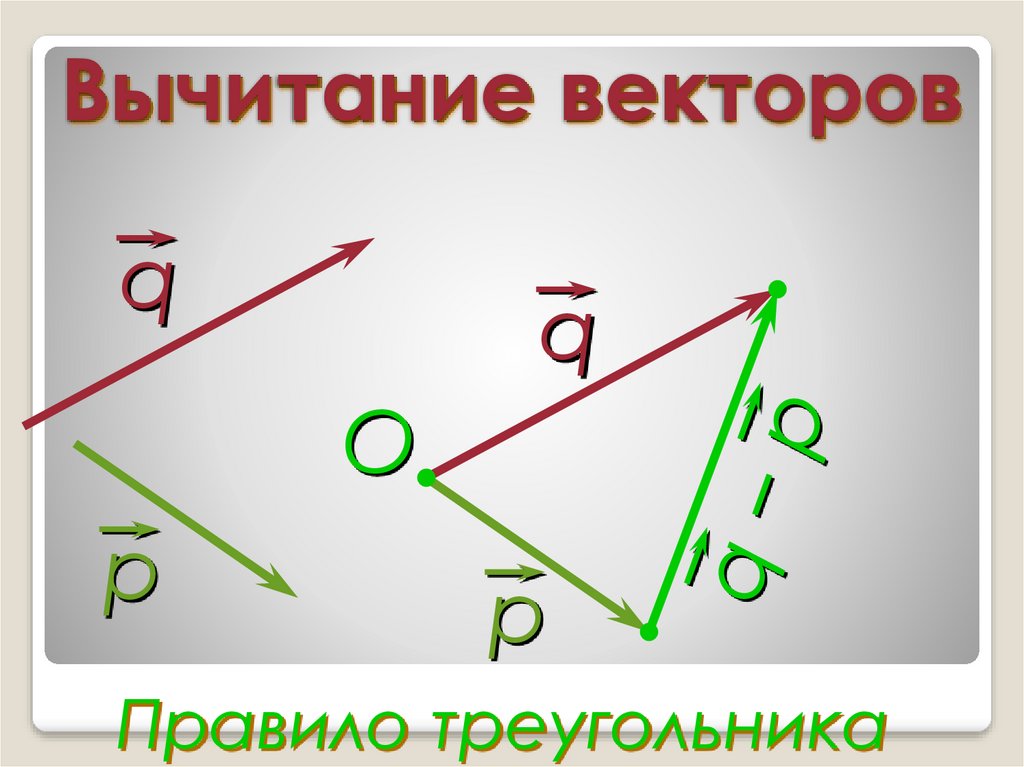
15. Вычитание векторов

q
q
O
р
р
Правило треугольника

16. Умножение вектора на число

Коллинеарны

17.

18.

Свойства умножения
(kn)а = k(na)
− сочетательный закон
k(а + b) = ka + kb
− первый распределительный закон
(k + n)а = ka + na
− второй распределительный закон