Похожие презентации:
Теоремы сложения и умножения вероятностей. (Лекция 3)
1. Теоремы сложения и умножения вероятностей
1. Условная вероятность.2. Теоремы умножения вероятностей.
3. Теоремы сложения вероятностей.
4. Формула полной вероятности.
Формула Байеса.
2. 1. УСЛОВНАЯ ВЕРОЯТНОСТЬ
16.05.16Ирина Юрьевна Хар
2
3. Условная вероятность
Вероятность события А при условии, чтособытие В с вероятностью Р(В) 0 уже
произошло, обозначается Р(А/В) и
называется условной вероятностью
события А при условии, что имело
место событие В.
16.05.16
Ирина Юрьевна Хар
3
4. Условная вероятность
В – событие "вынутый шар - белый",А1 -событие "шар вынимается из 1-ой урны",
А2 -событие "шар вынимается из 2-ой урны"
2
1
16.05.16
Ирина Юрьевна Хар
4
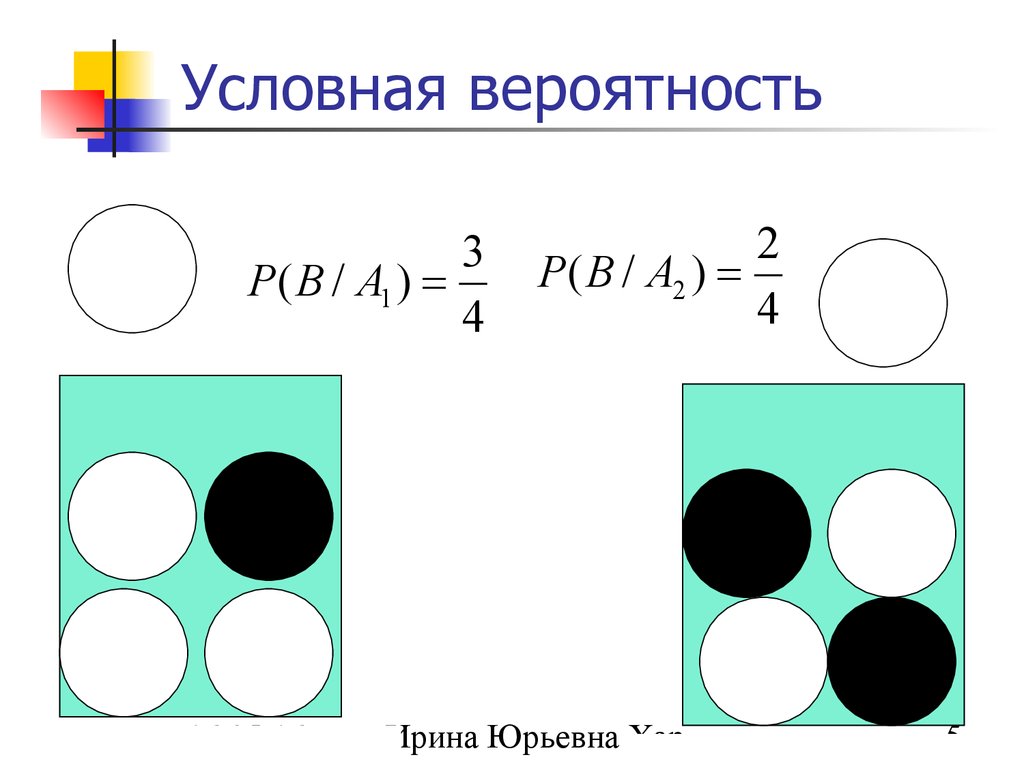
5. Условная вероятность
3P( B / A1 )
4
16.05.16
2
P( B / A2 )
4
Ирина Юрьевна Хар
5
6. События А и В называются независимыми
если осуществление одного не влияет навероятность осуществления другого, т.е.
P ( A / B ) P( A)
или
P ( B / A) P ( B )
7. 2. ПРОИЗВЕДЕНИЕ ВЕРОЯТНОСТЕЙ
16.05.16Ирина Юрьевна Хар
7
8. ТЕОРЕМА 1
Вероятность совместного появления двухсобытий равна произведению вероятности
одного из них на условную вероятность
другого, вычисленную в предположении,
что первое событие уже наступило.
P ( AB) P ( A) P ( B / A)
9.
А – «первая карта – дама»,В – «вторая карта дама»
4 3
1
P ( AB ) P ( A) P ( B / A)
36 35 1059
16.05.16
Ирина Юрьевна Хар
10. ТЕОРЕМА 2
Вероятность совместного появлениядвух независимых событий равна
произведению их вероятностей, т.е.
P ( AB) P ( A) P ( B )
11. ТЕОРЕМА 2
Усложненное строение буквы «а» за четповторения движения в овале Р(А)=0,06
Буква «д» с надстрочечным элементом
Р(В)=0,29
P ( A В ) 0,06 0,29 0,0174
16.05.16
Ирина Юрьевна Хар
11
12. ТЕОРЕМА 3
Если для двух событий выполняетсяравенство
P ( AB) P ( A) P ( B )
то эти события независимые.
13. ТЕОРЕМА 4
Вероятность совместного наступленияконечного числа событий равна произведению
вероятности одного из них на условные
вероятности всех остальных, причем условная
вероятность каждого последующего события
вычисляется в предположении, что все
предыдущие уже наступили, т.е.
P( A1 A2 ... An ) P( A1 ) P( A2 / A1 ) ... P( An / A1 A2 ... An 1 )
14.
ЮР
И
С
А1 – первая буква «ю»,
А2 – вторая буква «р»,
А3 – третья буква «и»,
А4 – третья буква «с»,
А5 – пятая буква «т».
В ‑ появится слово «юрист».
Т
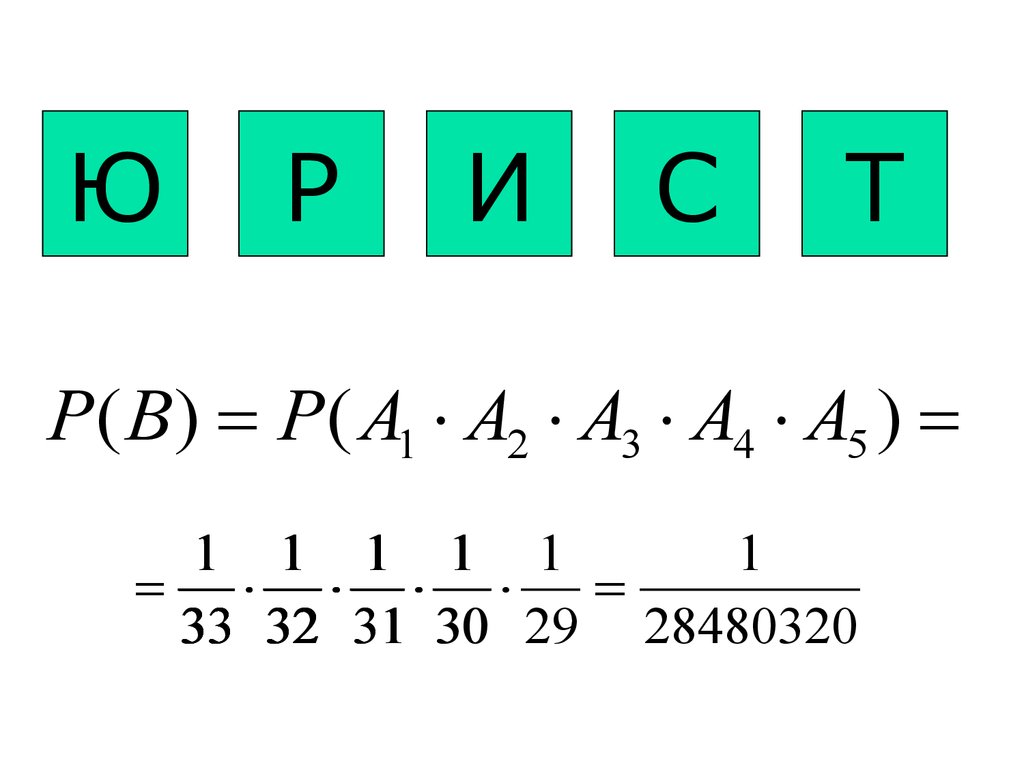
15.
ЮР
И
С
Т
P ( B ) P ( A1 A2 A3 A4 A5 )
1 1 1 1 1
1
33 32 31 30 29 28480320
16. ТЕОРЕМА 5
Вероятность совместного появления нескольсобытий, независимых в совокупности, равн
произведению вероятностей этих событий, т
P( A1 A2 A3 ... An ) P ( A1 ) P ( A2 ) P( A3 ) ... P( An )
17.
ЮР
И
С
Т
P ( B ) P ( A1 A2 A3 A4 A5 )
1
1 1 1 1
33 33 33 33 33
1
39135393
18. 3. СУММА ВЕРОЯТНОСТЕЙ
16.05.16Ирина Юрьевна Хар
18
19. ТЕОРЕМА 6
Вероятность появления одного из двухнесовместных событий, равна сумме
вероятностей этих событий, т.е.
P ( A B ) P ( A) P ( B )
20. 25 ЧЕЛОВЕК ИМЕЮТ СЛЕДУЮЩИЕ ОЦЕНКИ
ОТЛИЧНО -5
ХОРОШО -
10
УДОВЛЕТВОРИТЕЛЬНО - 10
21.
Какова вероятность того, чтонаугад вызванный курсант
отличник или хорошист?
22.
А – наугад вызванный курсант –отличник,
В – наугад вызванный курсант –
хорошист.
P( A B) P ( A) P( B)
5 / 25 10 / 25 0,6
23. ТЕОРЕМА 7
Вероятность появления одного изнескольких попарно несовместных
событий равна сумме вероятностей этих
событий
P( A1 A2 A3 ... An )
P( A1 ) P( A2 ) P( A3 ) ... P( An )
24. СЛЕДСТВИЕ
Сумма вероятностей попарнонесовместных событий, образующих
полную группу, равна 1:
P( A1 A2 A3 ... An ) 1
25.
Два стрелка стреляют по одной и той жецели. Вероятности поражения ими цели
соответственно равны 0,8 и 0,7.
Какова вероятность поражения цели?
26.
А1 – поражение цели первым стрелком,А2 – поражение цели вторым стрелком,
В – поражение цели вообще
B A1 A2
Р ( B) Р ( A1 ) Р( A2 )
0,8 0,7 1,5
1 !!!!
27. ТЕОРЕМА 8
Вероятность появления хотя бы одногоиз двух совместных событий равна
сумме вероятностей этих событий без
вероятности их совместного
наступления:
P ( A B ) P ( A) P ( B ) P ( AB)
28.
P( B) P( A1 ) P( A2 ) P( A1 A2 )0,7 0,8 0,7 0,8 0,94
29. СЛЕДСТВИЕ
В случае трех совместных событийвероятность их суммы вычисляется по
формуле:
P ( A B C ) P ( A) P ( B ) P (C )
P ( AB ) P ( AC ) P ( BC ) P ( ABC )
30. ТЕОРЕМА 9
Вероятность появления хотя бы одного изсобытий, независимых в совокупности, равна
разности между единицей и произведением
вероятностей противоположных событий:
P ( A1 A2 ... An ) 1 P ( A1 ) P ( A2 ) ... P ( An )
31.
P ( B ) 1 P ( A1 ) P ( A2 )1 0,3 0,2 0,94
32. 3. Формула полной вероятности. Формула Байеса
16.05.16Ирина Юрьевна Хар
32
33. ТЕОРЕМА 10
Вероятность события А, которое может наступитьтолько при условии появления одного из событий
В1, В2,...,Вn, образующих полную группу попарно
несовместных событий, равна сумме произведений
вероятностей каждого из этих событий на
соответствующую условную вероятность события
А, т.е.
P( A) P( B1 ) P( A / B1 )
P( B2 ) P( A / B2 ) ... P( Bn ) P( A / Bn )
34.
Вероятность того, что во время работы ПК произошелсбой:
в арифметическом устройстве 0,3,
в оперативной памяти – 0,2,
в остальных устройствах – 0,5.
Вероятности обнаружения сбоя в арифметическом
устройстве, в оперативной памяти и в остальных
устройствах соответственно равны 0,8, 0,9, 0,9.
Найти вероятность того, что возникший в ПК сбой
будет обнаружен.
35.
Обозначим через А событие – сбой будет обнаружен.Возможны следующие предположения (гипотезы):
В1 – сбой произошел в арифметическом устройстве,
В2 – сбой произошел в оперативной памяти,
В3 – сбой произошел в остальных устройствах.
Воспользуемся формулой полной вероятности:
P( A) P( B1 ) P( A / B1 ) P( B2 ) P( A / B2 )
P( B3 ) P( A / B3 )
0,3 0,8 0,2 0,9 0,5 0,9 0,87.
36. Алгоритм применения ф.Байеса
1. Выдвигают предположения –гипотезы В1, В2,...,Вn. Данные
гипотезы составляют полную
группу несовместных событий.
37. Алгоритм применения ф.Байеса
2. Устанавливают доопытные(априорные) вероятности данных
гипотез: из интуитивных или
каких-либо других соображений.
38. Алгоритм применения ф.Байеса
3. Проводят эксперимент, в результате которогопроисходит событие А.
Таким образом получают новую информацию, на
основании которой выполняют переоценку
доопытных вероятностей гипотез по формуле
Байеса:
P ( Bi ) P ( A / Bi )
P ( Bi / A)
P ( A)
39. Алгоритм применения ф.Байеса
P ( Bi ) P ( A / Bi )P ( Bi / A)
P ( A)
где Р(А) определяется по формуле
полной вероятности.
Т.о. заменяют доопытные (априорные)
вероятности гипотез послеопытными
(апостериорными).
40.
Вероятность обнаружить признак А в рукописи, выполненнойженщиной равна 0,1, а в рукописи, выполненной мужчиной
– 0,3.
На исследование поступила рукопись, в которой обнаружен
данный признак. Какова вероятность, что данная рукопись
выполнена женщиной? Какова вероятность, что данная
рукопись выполнена мужчиной?
41.
А – в рукописи обнаружен признак А;М – рукопись выполнена мужчиной;
Ж – рукопись выполнена женщиной.
P( M ) P( А / M )
P ( M / A)
P( Ж ) P( A / Ж ) P( М ) Р( А / М )
0,5 0,3
0,75
0,5 0,1 0,5 0,3
42.
А – в рукописи обнаружен признак А;М – рукопись выполнена мужчиной;
Ж – рукопись выполнена женщиной.
P( Ж ) Р( А / Ж )
P( Ж / A)
Р( Ж ) Р( А / Ж ) Р( M ) Р( А / M )
0,5 0,1
0,25
0,5 0,1 0,5 0,3









































 Математика
Математика Философия
Философия








