Обчислення обємів просторових тіл з допомогою інтеграла

1.

Обчислення обємів
просторових тіл з
допомогою інтеграла.
Воробьев Леонид Альбертович, г.Минск

2.

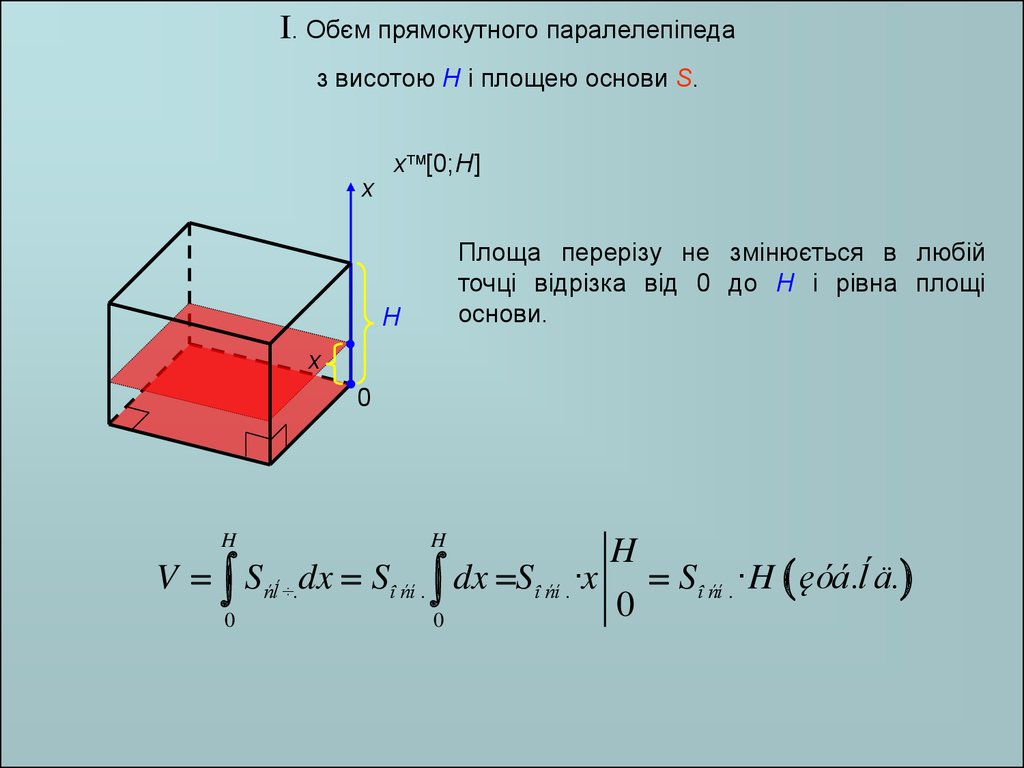
I. Обєм прямокутного паралелепіпеда
з висотою H і площею основи S.
x [0;H]
x
Площа перерізу не змінюється в любій
точці відрізка від 0 до H і рівна площі
основи.
H
x
0
H
H
0
0
V Sńĺ ÷.dx Sî ńí . dx Sî ńí . ·x
H
0
Sî ńí . ·H ęóá.ĺ ä.

3.

II. Обєм прямої призми
з висотою H і площею основи S.
x [0;H]
x
Площа перерізу не змінюється в любій
точці відрізка від 0 до H і рівна площі
основи.
H
x
0
H
H
0
0
V Sńĺ ÷.dx Sî ńí . dx Sî ńí . ·x
H
0
Sî ńí . ·H ęóá.ĺ ä.

4.

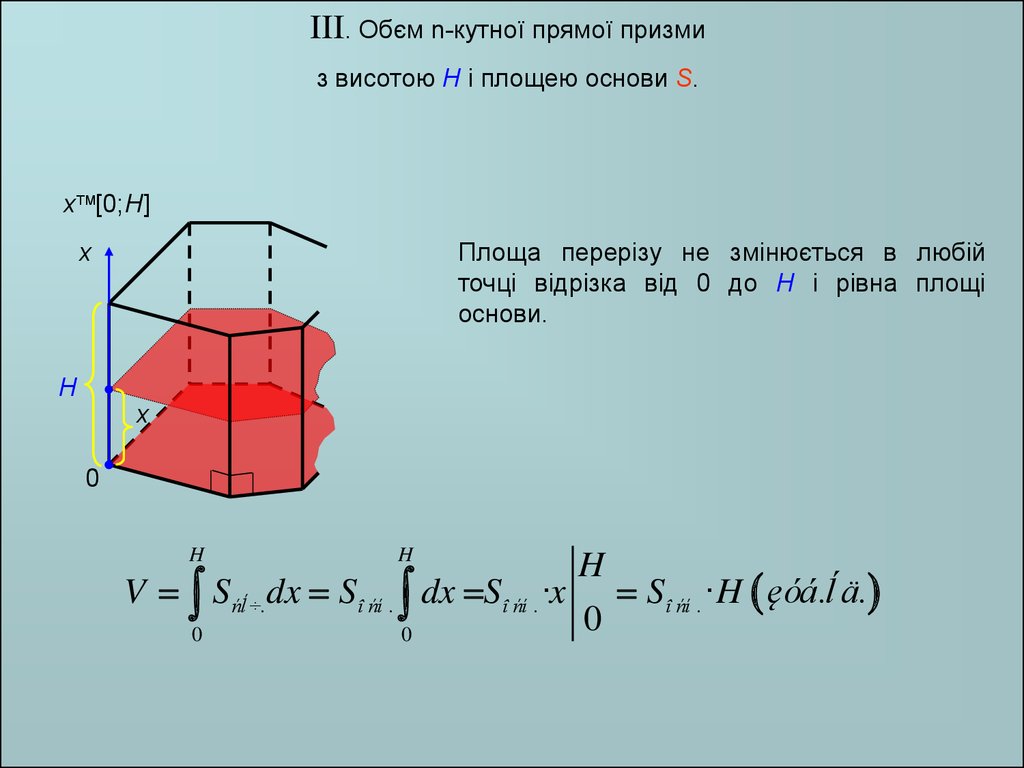
III. Обєм n-кутної прямої призми
з висотою H і площею основи S.
x [0;H]
Площа перерізу не змінюється в любій
точці відрізка від 0 до H і рівна площі
основи.
x
H
x
0
H
H
0
0
V Sńĺ ÷.dx Sî ńí . dx Sî ńí . ·x
H
0
Sî ńí . ·H ęóá.ĺ ä.

5.

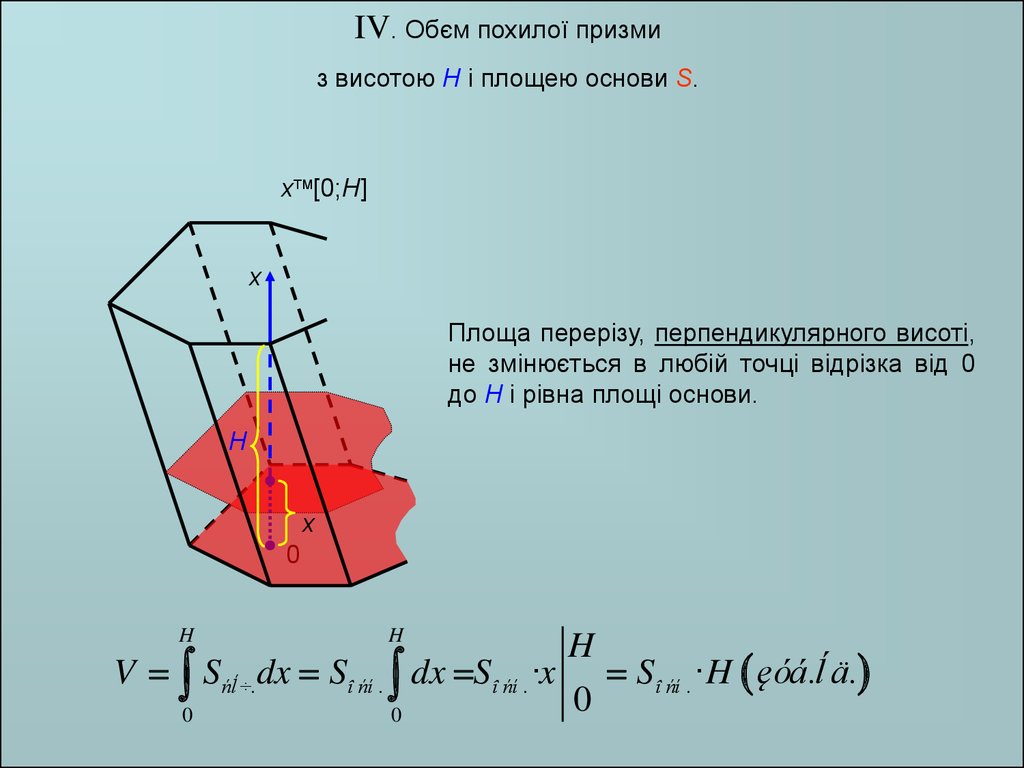
IV. Обєм похилої призми
з висотою H і площею основи S.
x [0;H]
x
Площа перерізу, перпендикулярного висоті,
не змінюється в любій точці відрізка від 0
до H і рівна площі основи.
H
x
0
H
H
0
0
V Sńĺ ÷.dx Sî ńí . dx Sî ńí . ·x
H
0
Sî ńí . ·H ęóá.ĺ ä.

6.

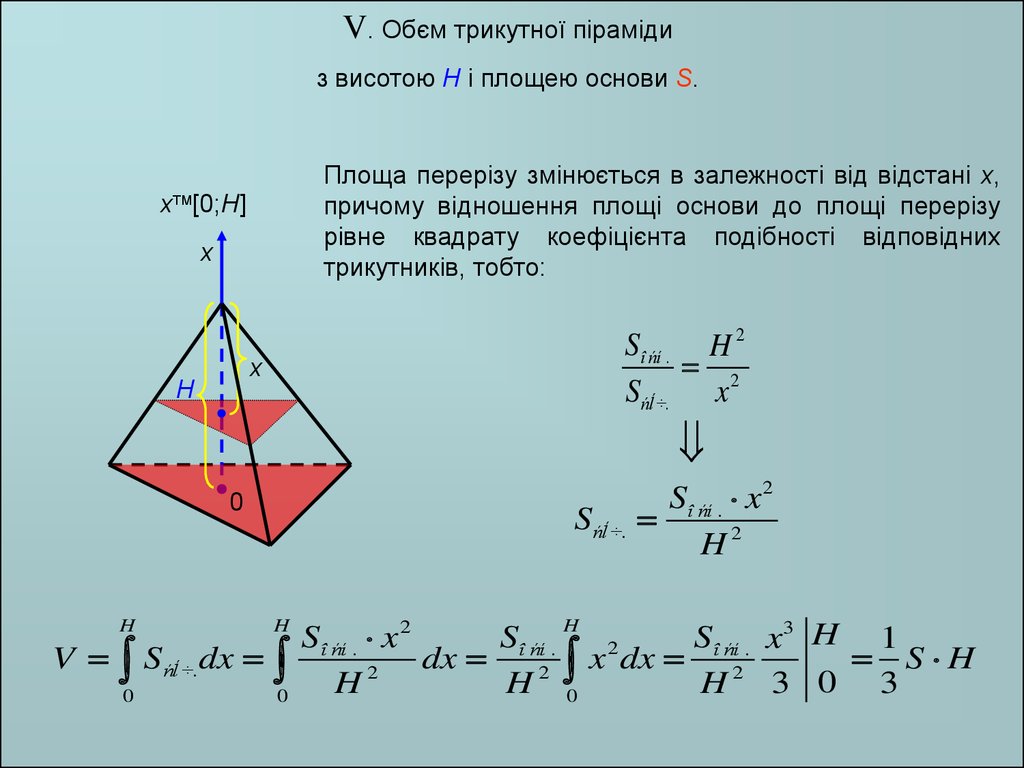
V. Обєм трикутної піраміди
з висотою H і площею основи S.
Площа перерізу змінюється в залежності від відстані x,
причому відношення площі основи до площі перерізу
рівне квадрату коефіцієнта подібності відповідних
трикутників, тобто:
x [0;H]
x
Sî ńí . H 2
2
Sńĺ ÷. x
x
H
0
H
V
S
0
Sńĺ ÷.
H
dx
ńĺ ÷.
0
Sî ńí . x 2
H2
H
Sî ńí . x 2
Sî ńí .
Sî ńí . x 3 H 1
2
dx
x dx
S H
2
2
2
H
H 0
H 3 0 3

7.

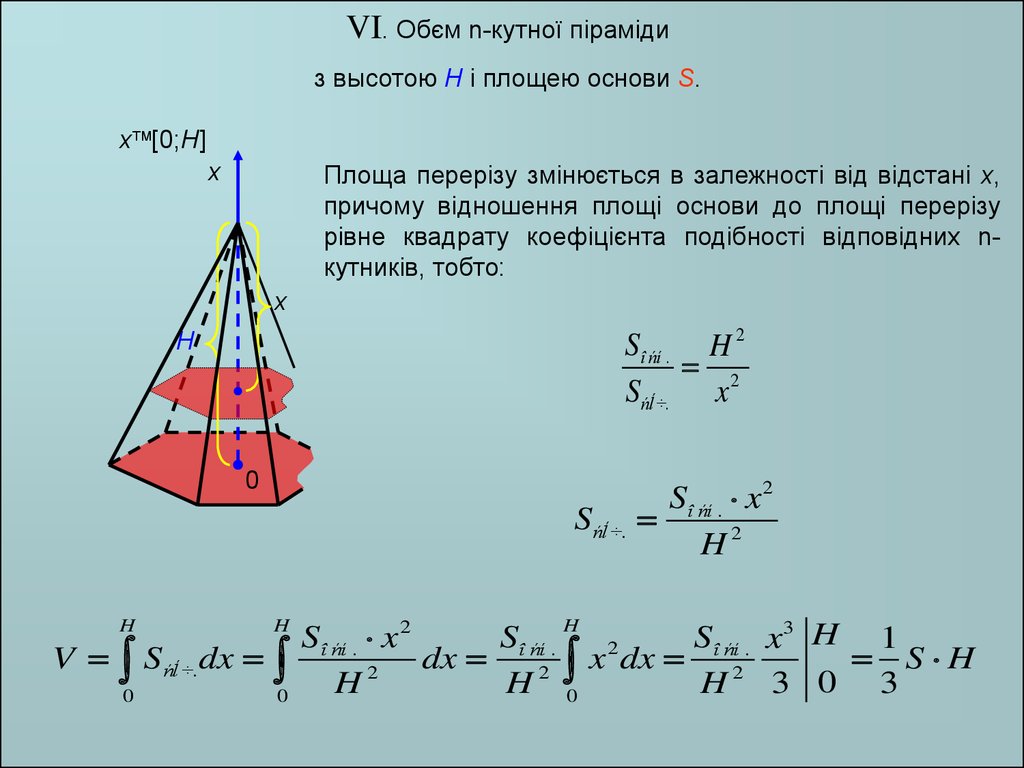
VI. Обєм n-кутної піраміди
з высотою H і площею основи S.
x [0;H]
Площа перерізу змінюється в залежності від відстані x,
причому відношення площі основи до площі перерізу
рівне квадрату коефіцієнта подібності відповідних nкутників, тобто:
x
x
Sî ńí . H 2
2
Sńĺ ÷. x
H
0
Sńĺ ÷.
H
V
S
0
H
dx
ńĺ ÷.
0
Sî ńí . x 2
H2
H
Sî ńí . x 2
Sî ńí .
Sî ńí . x 3 H 1
2
dx
x dx
S H
2
2
2
H
H 0
H 3 0 3

8.

VII. Обєм циліндра з висотою H і площею основи S.
x [0;H]
x
Площа перерізу не змінюється в любій
точці відрізка від 0 до H і рівна площі
основи.
H
x
0
H
H
0
0
V Sńĺ ÷.dx Sî ńí . dx Sî ńí . ·x
H
0
Sî ńí . ·H R 2 H ęóá.ĺ ä.

9.

VIII. Об’єм конуса з висотою H і площею основи S.
x [0;H]
Площа перерізу змінюється в залежності від відстані x,
причому відношення площі основи до площі перерізу
рівне квадрату коефіцієнта подібності відповідних
кругів, тобто:
x
x
Sî ńí . H 2
2
Sńĺ ÷. x
H
0
Sńĺ ÷.
H
V
S
0
H
dx
ńĺ ÷.
0
Sî ńí . x 2
H2
H
Sî ńí . x 2
Sî ńí .
Sî ńí . x 3 H 1
2
dx
x dx
S H
2
2
2
H
H 0
H 3 0 3

10.

IX. Обєм кулі з радіусом R.
Знайдемо обєм півкулі, як нескінченну інтегральну суму
площ перерізів з радіусом r, де:
r R 2 x 2 , x 0; R
x
R
Vďî ëóř ŕ đč˙
R
x
R
2
2
S
dx
r
dx
R
x
dx
ńĺ ÷.
2
0
r
R
0
0
2
3 R 3 2 R 3
x3 R
R x
ęóá.ĺ ä.
R
3 0
3
3
0
Значить, обєм всієї кулі рівний:
Vř ŕ đŕ
2 R3 4 R3
2·
ęóá.ĺ ä.
3
3

11.

X. Обєм кульового сегмента.
Виведення формули обєму кульового сегмента з
висотою h і радіусом основи r відрізняється від
виведення
обєму
півкулі
нижньою
границею
інтегрування. В даному випадку вона рівна R –h :
R
Vńĺ ăě ĺ í ň ŕ
hh
R h
x
R
Sńĺ ÷.dx
R
R h
r dx
2
ńĺ ÷.
R
R
2
x 2 dx
R h
3
3
h
R
2
R
x3 R
2
3
R R h
R
R x
3
3
3 R h
2 h3
2 R3
R 3 3R 2 h 3Rh 2 h3
2
3
R R h
Rh
3
3
3
h
h 2 R ęóá.ĺ ä.
3
Зверніть увагу, що в формулі обєму кульового сегмента використовується радіус
кулі (R), а не радіус основи сегмента (r)!