Похожие презентации:
Інтеграл та його застосування
1. Інтеграл та його застосування
2.
Історія розвитку понять інтеграла йінтегрального обчислення
Історія розвитку понять інтеграла й інтегрального
обчислення пов’язана з потребою в обчисленні
площ фігур, а також поверхонь і об’ємів довільних
тіл. Передісторія інтегрального обчислення сягає
глибокої давнини: ідеї інтегрального обчислення
можна знайти в роботах давньогрецьких учених
Евдокса Кнідського (бл.408-355 до н.е.) і Архімеда
(бл.287-212 до н.е.).
2
3. Короткі історичні відомості
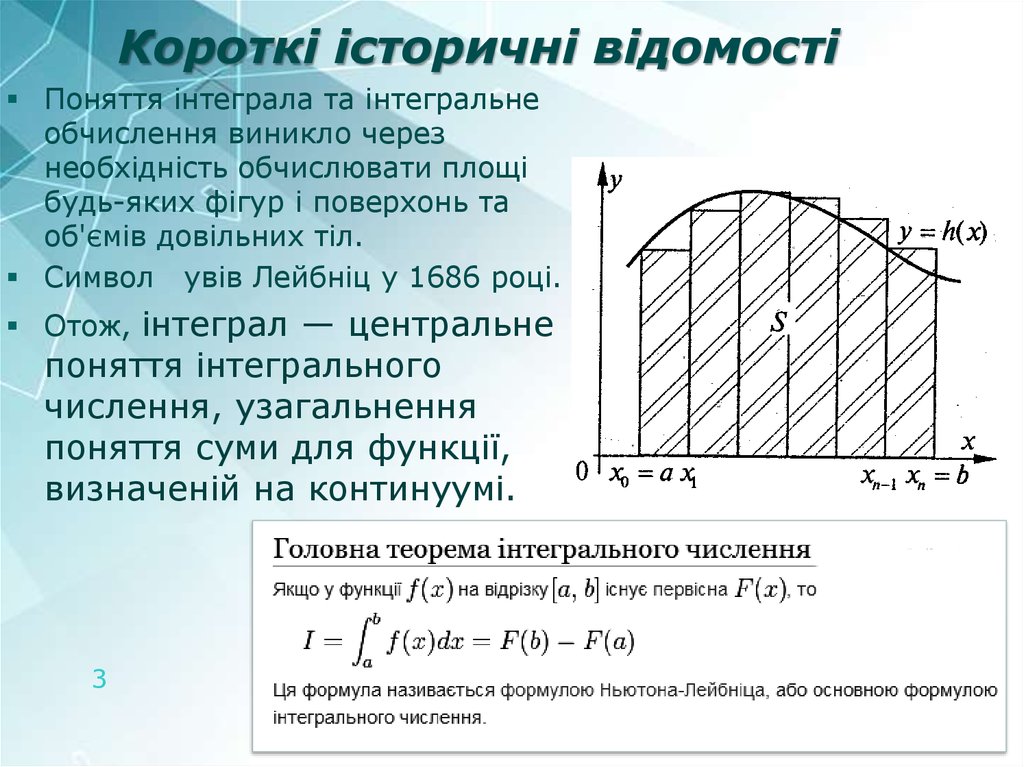
Поняття інтеграла та інтегральнеобчислення виникло через
необхідність обчислювати площі
будь-яких фігур і поверхонь та
об'ємів довільних тіл.
Символ увів Лейбніц у 1686 році.
Отож, інтеграл — центральне
поняття інтегрального
числення, узагальнення
поняття суми для функції,
визначеній на континуумі.
3
4.
Диференціювання функції f(x) – операціязнаходження її похідної .
Наприклад. Знайти похідну функції:
а) f ( x) x3 1; б) f ( x) cos 2 x .
Розв’язання
'
3
'
а) f ( x) ( x 1) 3x 2;
б) f ' ( x) (cos 2 x)' 2 sin 2 x .
Знаходження функції f(x) за даною її
похідною f ' ( x) називається операцією
інтегрування.
Операція інтегрування обернена до
операції диференціювання.
Наприклад.
а) Якщо f ' ( x) sin x , то f ( x) cos x ,
'
оскільки ( cos x) sin x .
1
'
б) Якщо f ( x) 2 x , то f ( x) x ,
оскільки ( x )' 1 .
2 x
Функція F(x) називається первісною для
функції f(x) на даному проміжку, якщо для
будь-якого х з цього проміжку
F ( x) f ( x)
'
Наприклад.
Функція F ( x) f ( x) 1 x 4 2
-
4
первісна для функції f ( x)
1
x
на
проміжку ( ; ) , оскільки при x ( ; )
'
1
F ( x) x 4 2 x 3 f ( x).
4
'
4
4
5.
Основна властивість первіснихЯкщо функція F(x) є первісною для
функції f(x) на даному проміжку, а С –
довільна стала, то функція F(x)+С також є
первісною для функції f(x), при цьому
будь-яка первісна для f(x) на даному
проміжку може бути записана у вигляді
F(x)+С, де С– довільна стала.
Вираз F(x)+С - загальний вигляд
первісної для функції f(x).
Наприклад.
Якщо F ( x) 2 x - первісна для функції
1
на проміжку (0; ) , то
x
1
первісною для функції f ( x) x
f ( x)
на
проміжку (0; ) є функція F ( x) 2 x C,
де С – довільна стала, оскільки
F ' ( x) (2 x C ) '
(2 x ) ' C ' 2
1
2 x
0
1
x
f ( x).
Геометричний зміст основної
властивості первісних
Графіки всіх первісних для даної
функції f(x) одержується з будь-якого з них
шляхом паралельного перенесення вздовж
осі Оу.
5
Сукупність усіх первісних даної функції
f(x) називається невизначеним
інтегралом.
Позначається: f ( x)dx ; тобто
f ( x)dx F ( x) C, де F(x) – одна з
первісних для функції f(x), С – довільна
стала.
- знак інтеграла, f(x) підінтегральна
функція, f(x)dx – підінтегральний вираз.
Наприклад.
3
4
F ( x) x 4 а) 4 x dx x C , оскільки
3
4 '
3
первісна функції f ( x) 4 x (( x ) 4 x ).
б) cos xdx sin x C, оскільки F ( x) sin x первісна для функції '
f ( x) cos x((sin x) cos x).
6.
Таблиця первісних (невизначених інтегралів)Функція f(x)
Загальний вигляд первісних
F(x)+С, де С - стала
0
С
0 dx C
1
х+С
dx x C
x ( 1, R)
x 1
C
1
1
x
1
x
ln x C
sin x
cos x C
cos x
sin x C
2 x C
1
sin 2 x
1
cos 2 x
ctgx C
ex
ex C
a x (a 0, a 1)
tgx C
ax
C
ln a
Запис за допомогою
невизначеного інтеграла
x 1
x dx 1 C; ( 1, R)
1
x dx ln x C
1
dx 2 x C
x
sin xdx cos x C
cos xdx sin x C
1
sin
2
x
dx ctgx C
1
cos
e
dx tgx C
2
x
x
ex C
x
a
ax
C
ln a
6
7. Правила знаходження первісних (правила інтегрування)
1. Якщо F - первісна функції f (x) , а G –первісна функції g (x ) , то F+ G –
первісна функції
Інтеграл від суми дорівнює сумі
інтегралів від доданків, тобто
( f ( x) g ( x))dx
f ( x) g ( x)
f ( x)dx g ( x)dx
Наприклад.
Знайти первісну для функції:
а) f ( x) 1 x ; б) f ( x) sin x cos x .
x
Розв’язання
x2
а) F ( x) ln x 2 C ;
б) F ( x) cos x sin x C .
Наприклад.
Обчислити:
1
x
а) e x 1 dx; б) sin 2 x a dx .
x
Розв’язання
а) e x 1 dx e x dx 1 dx
x
x
e x 2 x C;
б) 12 a x dx 12 dx a x dx
sin x
7
ctgx
ax
C.
ln a
sin x
8. Правила знаходження первісних (правила інтегрування)
2. Якщо F - первісна функціїf (x), а k і b –
сталі, то kF – первісна для функції kf (x) .
Наприклад.
Знайти первісну для функції:
4
1 x
а) f ( x) 2 ; б) f ( x) a .
cos x
5
Розв’язання
а) F ( x) 4tgx C ;
x
x
б) F ( x) 1 a C a C.
5 ln a
Сталий множник виноситься за знак
інтеграла, тобто (kf ( x)) dx k f ( x)dx , де k –
стала.
5 ln a
Наприклад. Обчислити:
а) 35 x 6 dx ; б) 1 dx .
4
x
Розв’язання
7
а) 35 x6dx 35 x5dx 35 x C
7
5 x C;
б) 1 dx 1 1 dx 1 2 x C
4 x 4 x 4
x
C.
2
7
8
9. Правила знаходження первісних (правила інтегрування)
f ,(xа) k і b –3. Якщо F - первісна функції
1
сталі (k 0) , то F (kx b) - первісна для
функції f (kx b) . k
Наприклад. Знайти первісну для функції:
а)f ( x) (2 x 3)
4
3
; б)f ( x) cos 4 x
Розв’язання
(2 x 3) 5
(2 x 3) 4 1 1
C
C
а)F ( x)
10
4 1
2
;
б)F ( x) sin 3 x 1 C 4 sin 3 x C
3
.
4
3
4
4
1
(kx b)dx k F (kx b) C
Наприклад. Обчислити:
а) (7 x 9)3dx ; б) a 2 x dx .
Розв’язання
а) (7 x 9)3dx (7 x 9) 1 C
4
4
7
(7 x 9)
C
28
2x
2x
б) a 2 x dx a 1 C a C
ln a 2
2 ln a
9
.
4
10. Криволінійна трапеція та її площа
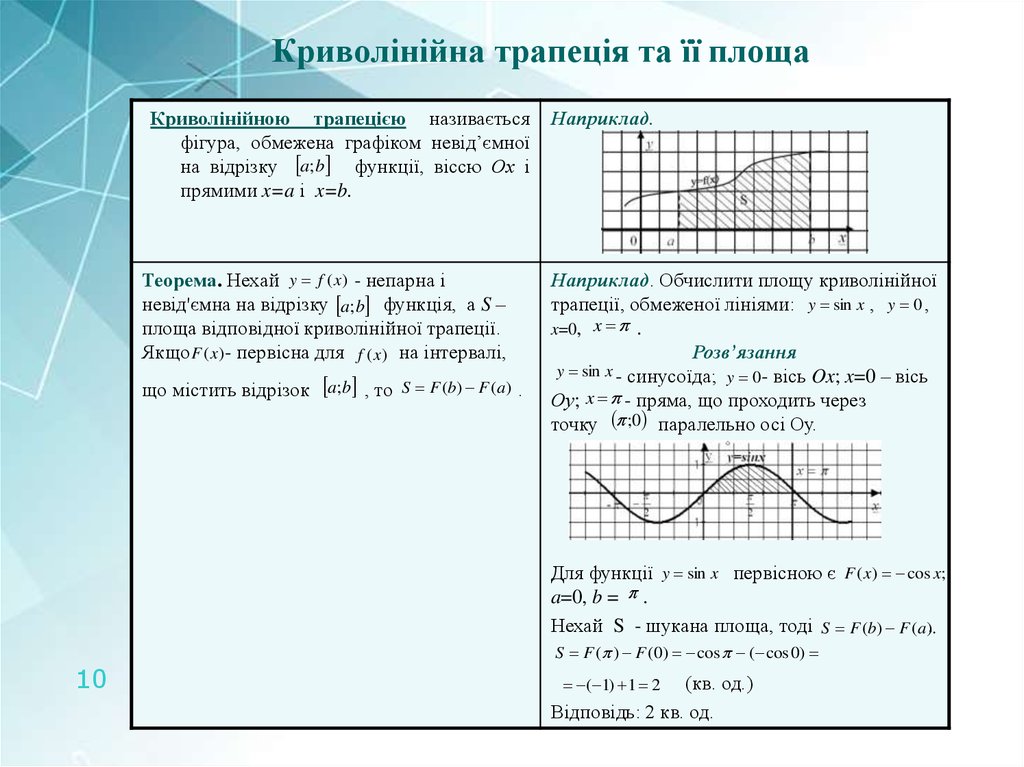
Криволінійною трапецією називаєтьсяфігура, обмежена графіком невід’ємної
на відрізку a; b функції, віссю Ох і
прямими x=a і x=b.
Теорема. Нехай y f (x) - непарна і
невід'ємна на відрізку a; b функція, а S –
площа відповідної криволінійної трапеції.
Якщо F (x) - первісна для f (x) на інтервалі,
що містить відрізок a; b , то S F (yb ) sinF (xa) .
Наприклад.
Наприклад. Обчислити площу криволінійної
трапеції, обмеженої лініями: y sin x , y 0 ,
x=0, x .
Розв’язання
y sin x - синусоїда; y 0- вісь Ox; x=0 – вісь
Оу; x - пряма, що проходить через
точку ;0 паралельно осі Оу.
Для функції y sin x первісною є F ( x) cos x;
a=0, b = .
Нехай S - шукана площа, тоді S F (b) F (a)..
S F ( ) F (0) cos ( cos 0)
10
(кв. од.)
Відповідь: 2 кв. од.
( 1) 1 2
11. Визначений інтеграл
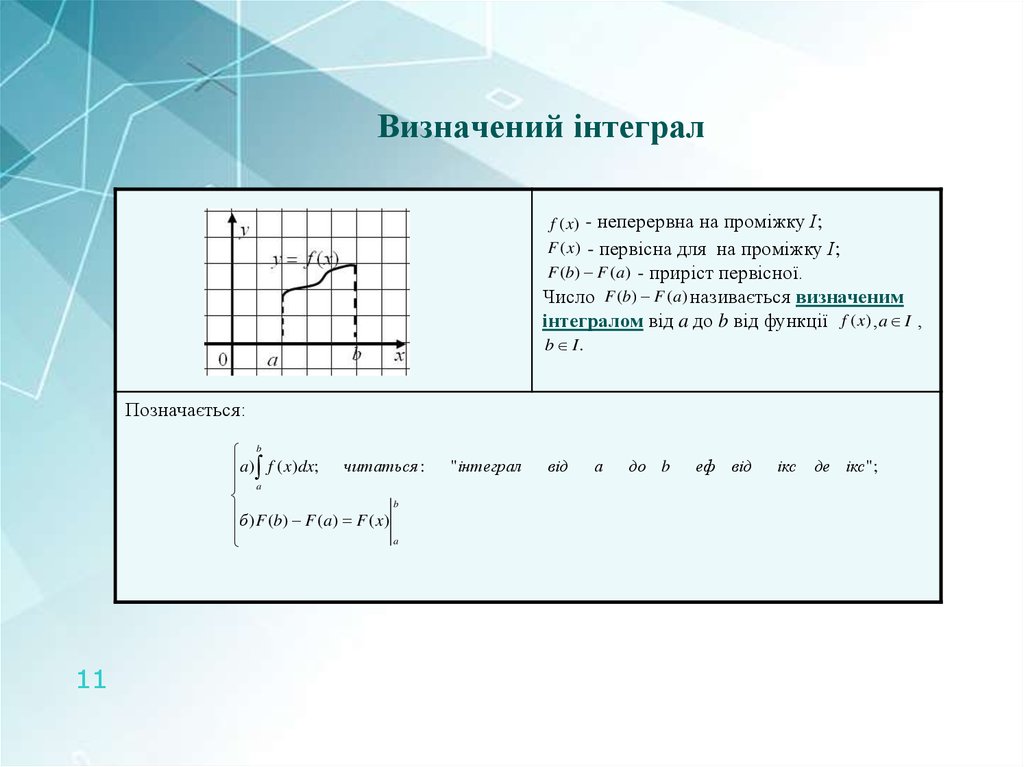
f (x) - неперервна на проміжку І;F (x ) - первісна для на проміжку І;
F (b) F (a ) - приріст первісної.
Число F (b) F (a) називається визначеним
інтегралом від a до b від функції f (x) , a I ,
b I.
Позначається:
b
a) f ( x)dx; читаться :
a
b
б ) F (b) F (a) F ( x)
a
11
"інтеграл
від
а
до b
еф від
ікс
де ікс ";
12. Формула Ньютона - Лейбніца
bb
a
a
f ( x)dx F ( x)
f (x) - підінтегральна функція;
f ( x)dx - підінтегральний вираз;
a - нижня межа інтегрування;
b - верхня межа інтегрування;
x – змінна інтегрування.
Основні властивості визначених інтегралів
b
b
b
a
a
a
1) ( f ( x) g ( x))dx f ( x)dx g ( x)dx
b
b
a
a
2) kf ( x)dx k f ( x)dx , (k – стала);
12
13. Обчислення об’ємів за допомогою визначеного інтеграла
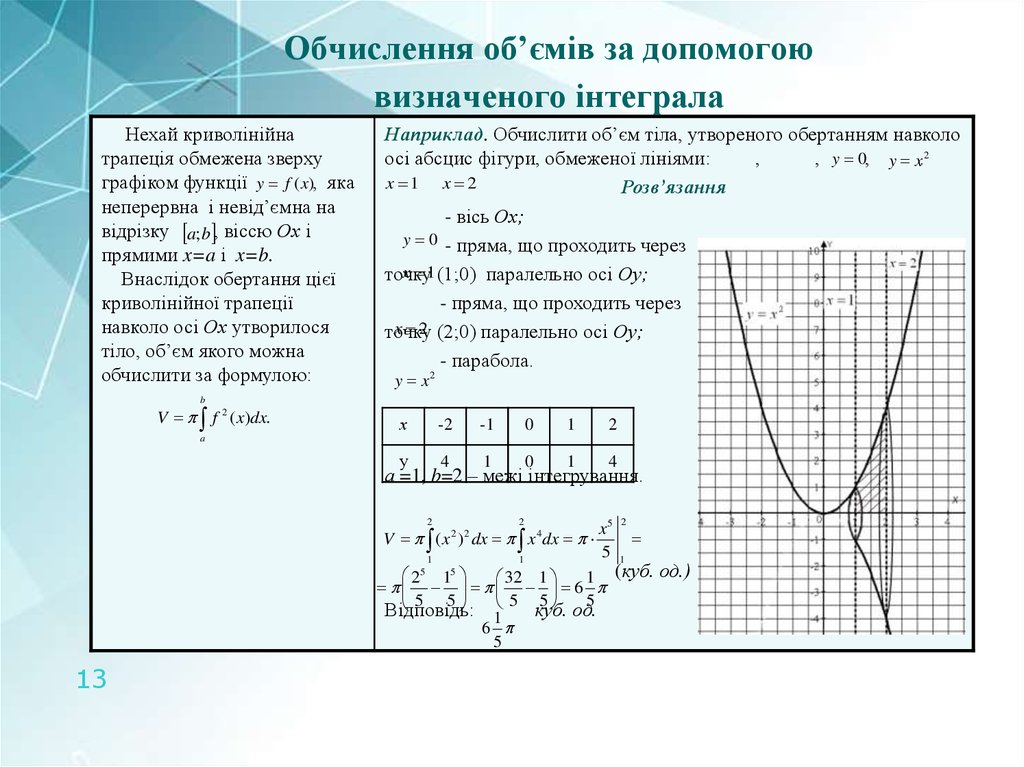
Нехай криволінійнатрапеція обмежена зверху
графіком функції y f (x), яка
неперервна і невід’ємна на
відрізку a; b , віссю Ох і
прямими x=a і x=b.
Внаслідок обертання цієї
криволінійної трапеції
навколо осі Ох утворилося
тіло, об’єм якого можна
обчислити за формулою:
Наприклад. Обчислити об’єм тіла, утвореного обертанням навколо
осі абсцис фігури, обмеженої лініями:
,
, y 0, y x.2
x 1 x 2
Розв’язання
- вісь Ох;
y 0 - пряма, що проходить через
x 1 (1;0) паралельно осі Оу;
точку
- пряма, що проходить через
x 2 (2;0) паралельно осі Оу;
точку
- парабола.
y x2
b
V f 2 ( x)dx.
х
-2
-1
0
1
2
у
4
1
0
1
4
a
а =1, b=2 – межі інтегрування.
2
2
1
1
V ( x 2 ) 2 dx x 4 dx
x5
5
2
1
25 15
1 (куб. од.)
32 1
6
5
5
5 куб.
5 5
Відповідь:
од.
1
6
5
13
14.
Обчисленняплощ
плоских
фігур
Застосування
в економіці
й техніці
Обчислення
кількості
електрики
та кількості
теплоти
Застосування
визначеного
інтеграла
Обчислення
об'ємів тіл
14
Обчислення
відстані
за відомим
законом
зміни
швидкості
Обчислення
роботи
змінної
сили та
потужності
15.
Інтеграл виник з практичної потребизнаходити площі неплоских фігур.
Найбільший внесок у вивченні інтегрального
числення вніс Архімед.
Одного разу, прийшовши із рибалки, Архімед
захотів визначити найбільш точно площу
поверхні риби.
15
16.
Розбивши поверхню риби на прямокутники, він знайшов їхплощі, причому чим більшою була кількість прямокутників, тим
точнішим було значення площі.
16
17.
1718.
1. Обчислення шляху за відомимзаконом зміни швидкості.
S
t2
v
(
t
)
dt
t1
18
19.
Розв'яжемо задачу:Тіло рухається прямолінійно зі швидкістю, яка
змінюється за законом v=2t+1(м/с). Знайти шлях,
який пройшло тіло за інтервал часу від t 1 =1c, до
t2 =3c.
2
t
( 2t 1) dt (2
t
)
s
2
3
3
1
19
1
(9 3 (1 1)) 10( м).
20.
2. Обчислення роботи змінноїсили.
b
A
F
(
x
)
dx
a
20
21.
Розв'яжемо задачу:Обчислити роботу, яку треба виконати, щоб
викачати воду з ями глибиною 4м, що має
квадратний переріз із стороною 2м. Густина
води ρ=103 кг/м3 .
4
А(
g ( 4
x
) dx
4 g ( 4 x )
F
x) 4 S
H
g
осн.
x
0
2
2
0;4 ,
g x9,8 м / с
g (4 x
) 4 g (16 8)
4
4
2
0
32 10 3 9,8 313,6 10 3 ( Дж )
21
3,1 10 5 ( Дж ).
22.
3. Обчислення масинеоднорідного стержня.
якщо
(l ) густина
l2
то
m (l )dl
l1
22
стержня,
23.
Розв'яжемо задачу:Знайти масу стержня завдовжки 35см, якщо
його лінійна густина змінюється за законом
ρ(l)=(4l+3)(кг/м)
0 , 35
m
(4l 3)dl (2l 3l )
0
1,295 1,3(кг )
23
2
0 , 35
0
24.
4. Обчислення кількостіелектрики.
q
t2
I
(
t
)
dt
.
t1
24
25.
Розв'яжемо задачу:Знайти кількість електрики, що проходить
через поперечний переріз провідника за
10с, якщо сила струму змінюється за
законом I(t)=(4t+1)(A)
10
q (4t 1)dt (2t
0
25
2
t )
10
210( Кл)
0
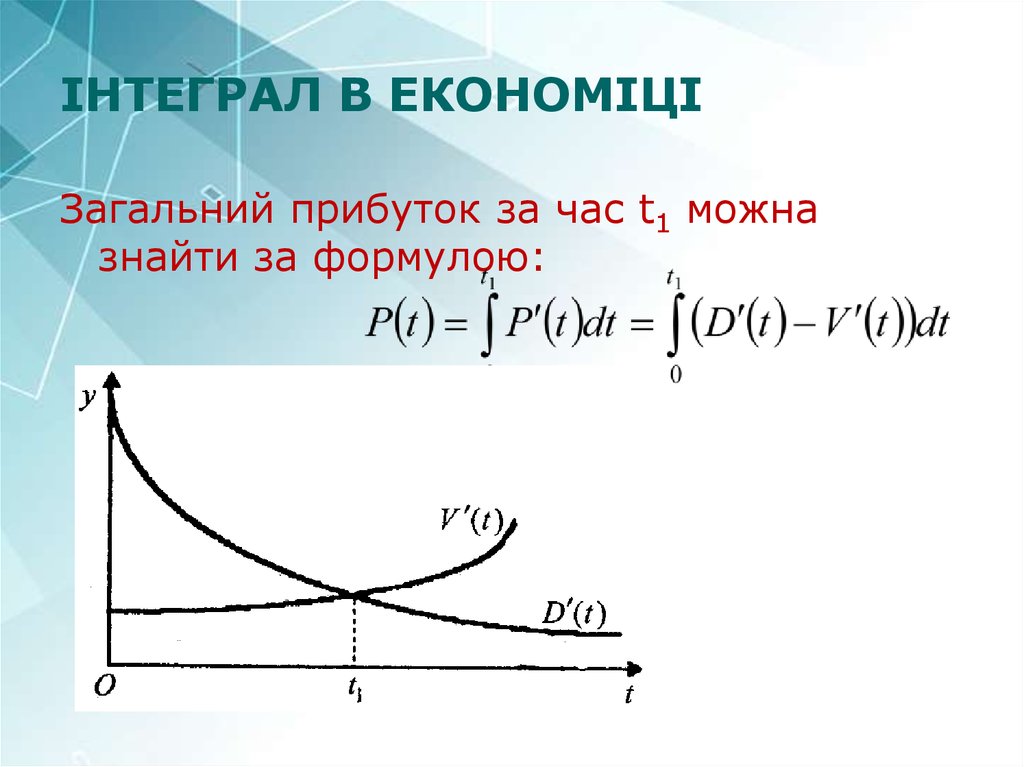
26. ІНТЕГРАЛ В ЕКОНОМІЦІ
Загальний прибуток за час t1 можназнайти за формулою:
26
27. ІНТЕГРАЛ В БІОЛОГІЇ
Середня довжина шляху, який пролітають птахи,перетинаючи деяку фіксовану ділянку,
обчислюється за формулою:
f x f x dx
b
2
L
27
a
b a
R 2
2R
R
2
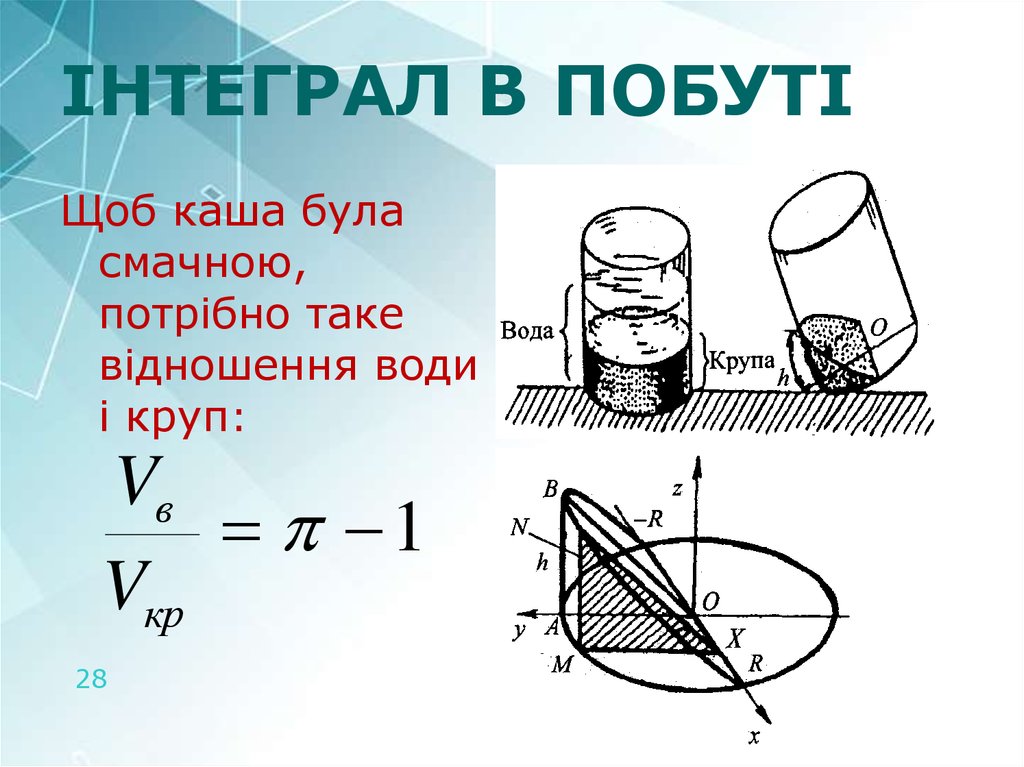
28. ІНТЕГРАЛ В ПОБУТІ
Щоб каша буласмачною,
потрібно таке
відношення води
і круп:
Vв
1
Vкр
28
29.
.Приклад 1 Експериментально встановлено, що продуктивність
праці робітника наближено виражається формулою
f(t)= -0.0033t2 - 0.089t + 20.96, де t — робочий час у годинах.
Обчислити обсяг випуску продукції за квартал, вважаючи
робочий день восьмигодинним, а кількість робочих днів у
кварталі — 62.
Розв'язання. Обсяг випуску продукції протягом зміни є
первісною від функції, що виражає продуктивність праці.
Тому
Протягом кварталу обсяг
випуску продукції
становитиме:
=62(-0.001∙512 -2.848 + 167.68)
29
= 62∙164.27≈ 10185 (од.).
30.
Приклад 2Експериментальне встановлено, що залежність витрати
бензину автомобілем від швидкості на 100 км шляху
визначається формулою Q = 18 - 0,3v +0,003v2, де 30 ≤ v ≤110.
Визначити середню витрату бензину, якщо швидкість руху 50 60 км/год.
Розв'язання. Середня витрата бензину становить
= 1/10(18∙60-0.3∙1800+0.003∙72000-18∙50-0.3∙12500.003∙41667) =
= 1/10(1080-540 + 216-900 + 375- 125) = 10,6 (л).
Отже, автомобіль на 100 км шляху, рухаючись зі
30
швидкістю
50 - 60 км/год, витрачає в середньому 10,6 л
бензину.
31.
Обчислити роботу, яку требавиконати, щоб викачати воду з ями
глибиною 4м., що має квадратний
переріз зі стороною 2м. Густина води
ρ=103кг/м3.
Розв'язання: Спрямуємо вісь Ох
вздовж діючої сили. Значення сили
F(x), що діє на переріз прямокутного
паралелепіпеда площею 4 м2,
визначається вагою шару води, що
знаходиться вище від цього перерізу.
Отже
F ( x) 4 g (4 x), де _ х 0;4 , g 9,8 м / с 2
x2 4
|0
A 4 g (4 x)dx 4 g 4 x
2
0
4 g (16 18) 32 103 9,8 313,6 103 ( Дж )
4
31
3,1 105 ( Дж )














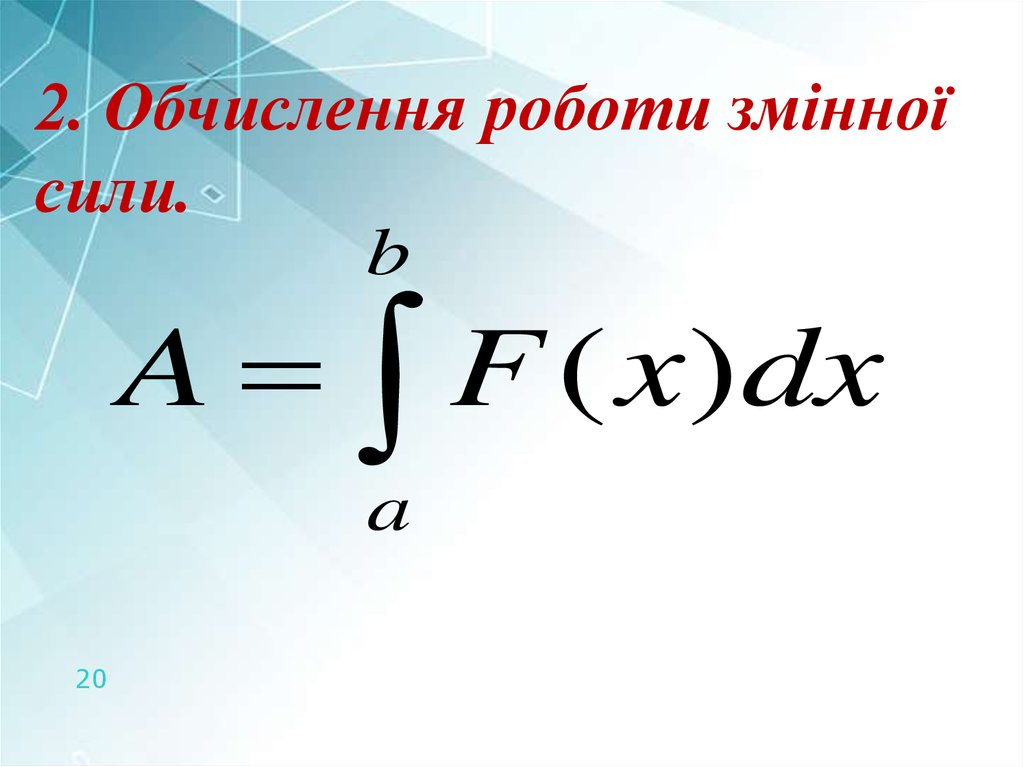



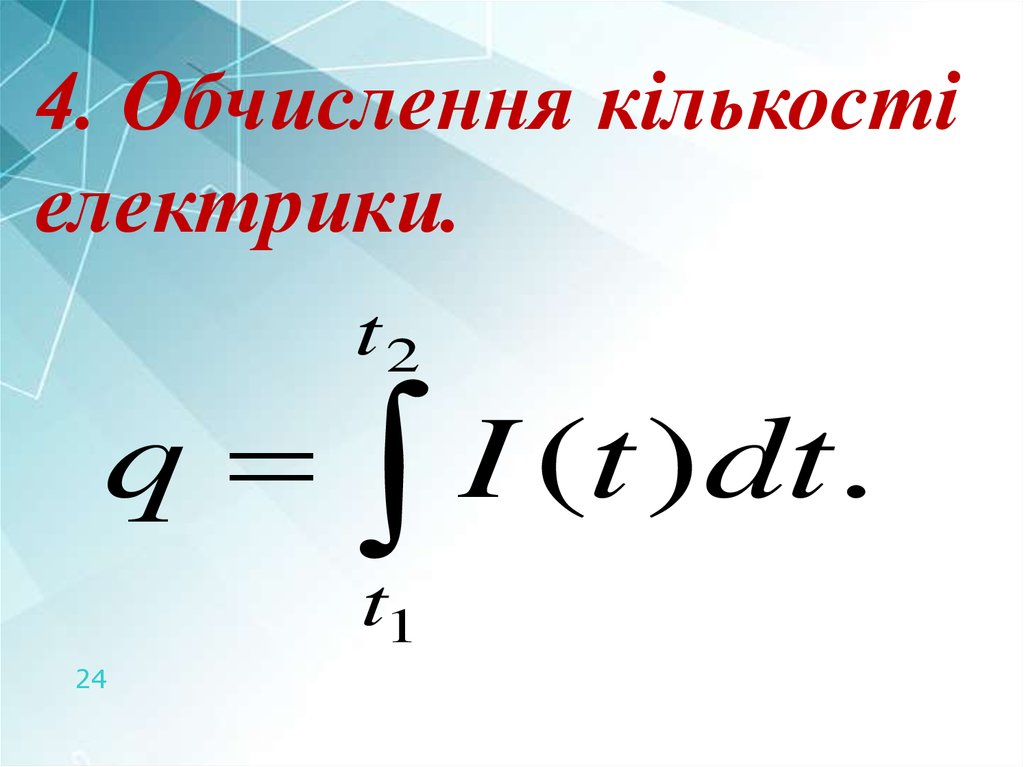










 Математика
Математика








