Многогранник. Призма

1.

2. Природа говорит языком математики: буквы этого языка – круги, треугольники и иные математические фигуры Галилей

3.

Комната
Прямоугольный
параллелепипед

4.

Карандаш
Шестиугольная
призма

5.

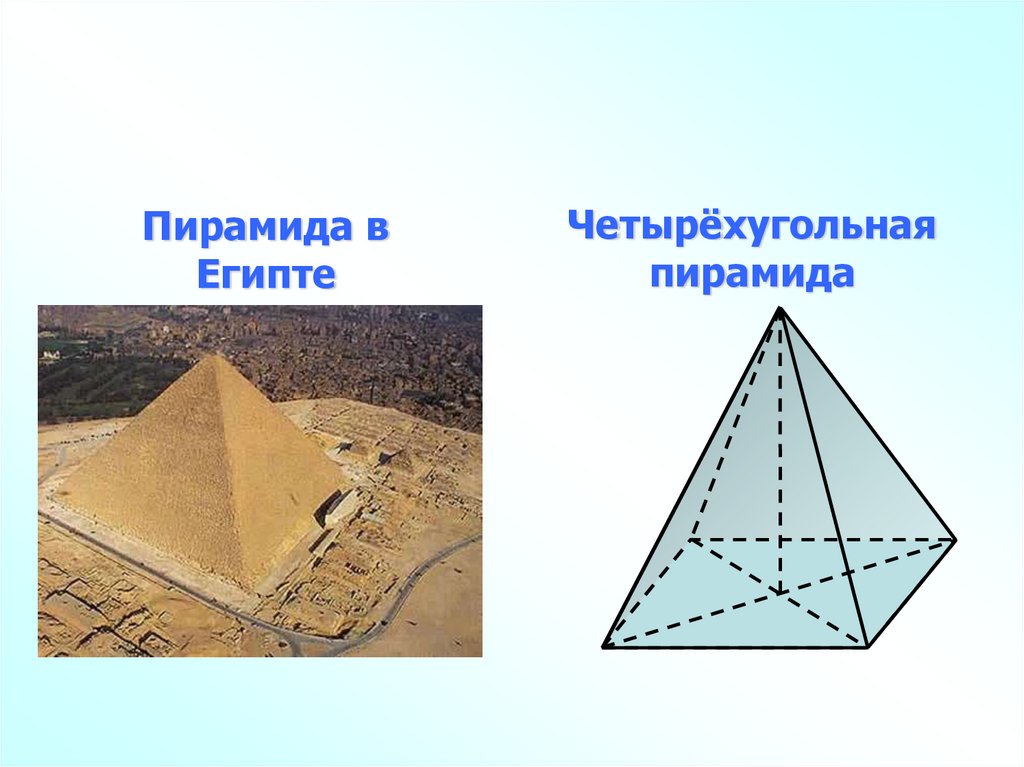
Пирамида в
Египте
Четырёхугольная
пирамида

6.

Земля
Шар

7.

Типи
Конус

8.

Цилиндр
консервы

9. Кристаллы

Халькопирит
Медный
купорос
Авгит
Топаз
Пирит

10.

«Мой дом
построен по
законам самой
строгой
архитектуры.
Сам Евклид мог
бы поучиться,
познавая
геометрию
моих сот».

11. Многогранники в ювелирном деле

12.

Фигуру в пространстве (тело)
надо представлять себе как
часть пространства, занятую
физическим телом и
ограниченную поверхностью.
Многогранник - это такое тело,
поверхность которого состоит из
конечного числа плоских
многоугольников.

13.

Параллелепипед
Поверхность,
составлена из
шести
параллелограммов.

14.

Тетраэдр
Поверхность,
составлена из
четырех
треугольников.
SS
В
А
С

15.

Многогранник
называется
выпуклым,
если он
расположен по
одну сторону
плоскости
каждого
плоского
многоугольника
на его
поверхности.

16. Тела Архимеда

17.

Невыпуклый многогранник

18. невыпуклые многогранники (тела Кеплера-Пуансо)

19. Многоугольники, из которых состав-лен многогранник, называются гранями многогранника.

Многоугольники, из которых составлен многогранник, называются
гранями многогранника.
D1
С1
В1
А1
С
D
А
В
грань

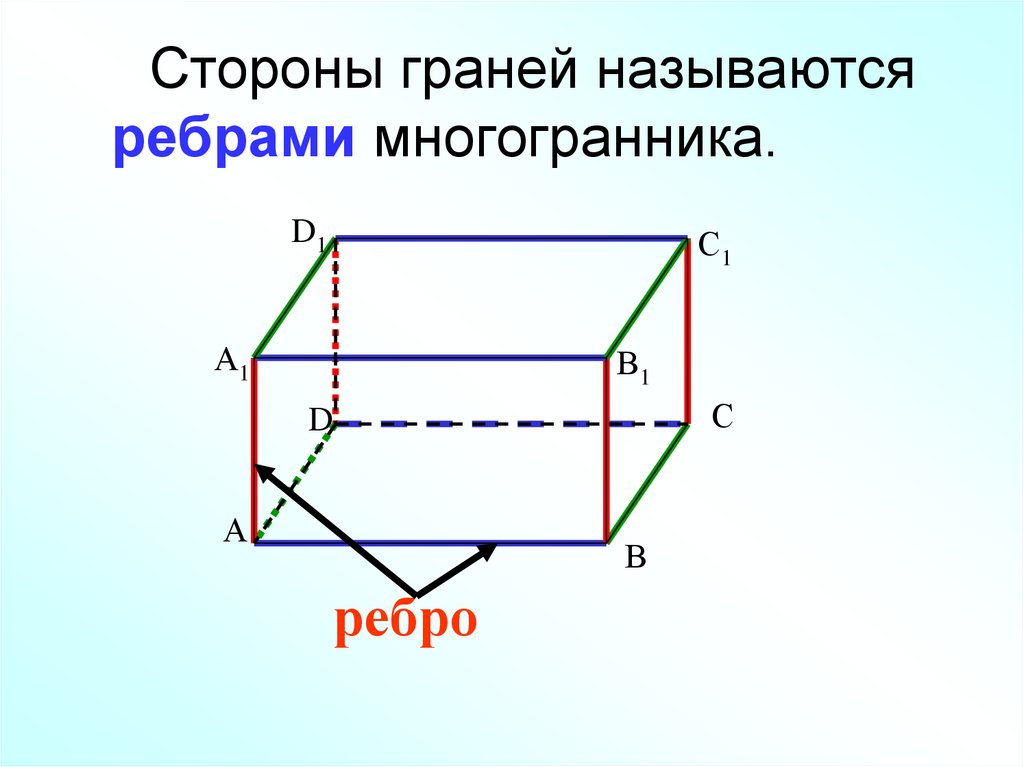
20. Стороны граней называются ребрами многогранника.

D1
С1
А1
В1
С
D
А
В
ребро

21. Вершины граней называются вершинами многогранника.

D1
А1
С1
В1
D
С
А
В
вершина

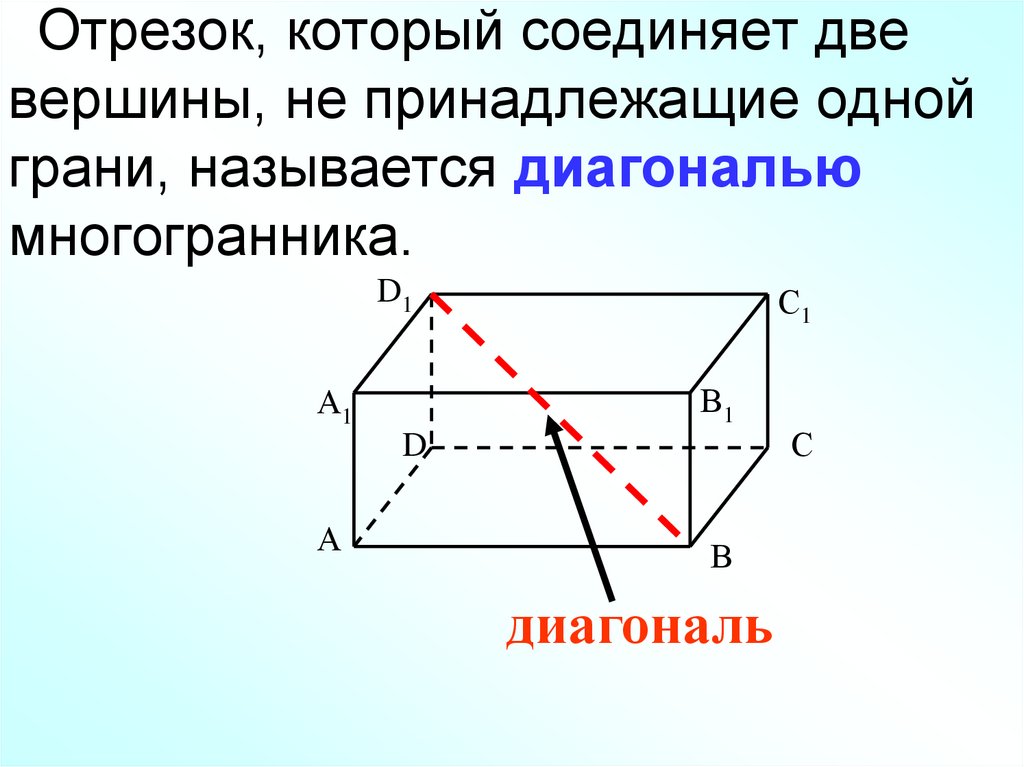
22. Отрезок, который соединяет две вершины, не принадлежащие одной грани, называется диагональю многогранника.

D1
С1
В1
А1
D
А
В
диагональ
С

23.

Октаэдр

24.

Страница 68
Из плоских многоугольников…
Простейшим многогранникам…

25.

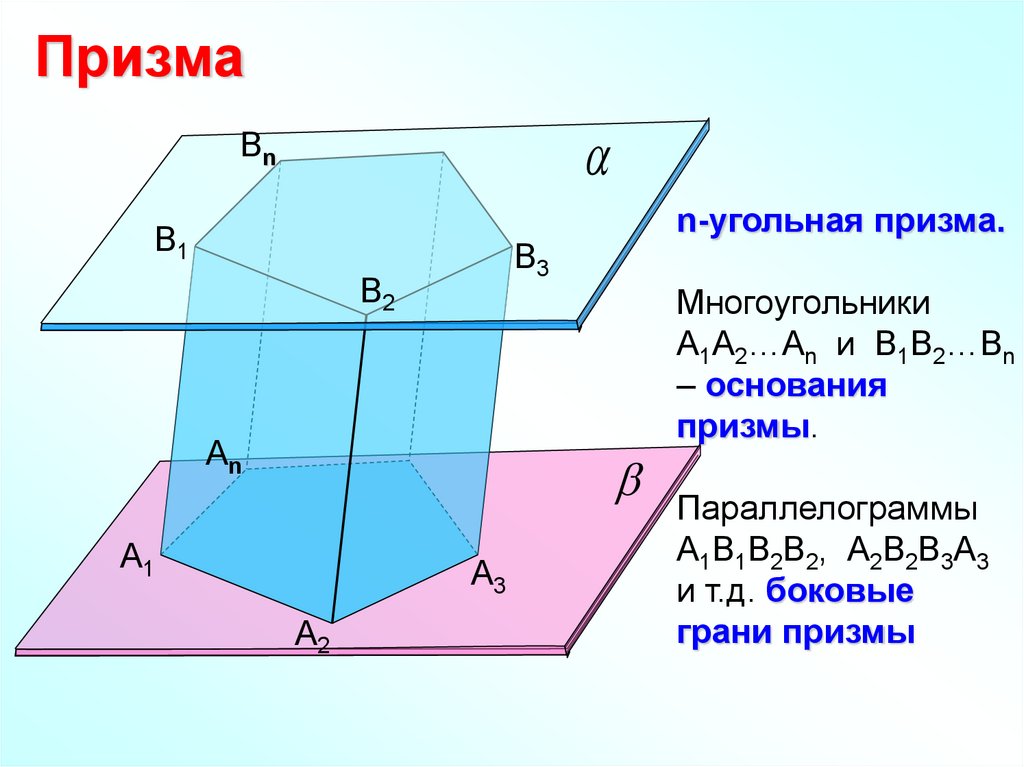
Призма
Bn
n-угольная призма.
B1
B3
B2
Многоугольники
А1А2…Аn и В1В2…Вn
– основания
призмы.
Аn
А1
А3
А2
Параллелограммы
А1В1В2В2, А2В2В3А3
и т.д. боковые
грани призмы

26.

Отрезки А1В1, А2В2 и т.д. боковые ребра призмы
Призма
Bn
Перпендикуляр,
проведенный из какойB3 нибудь точки одного
основания к плоскости
другого основания,
называется высотой
призмы.
B1
B2
Аn
А1
А3
А2

27.

Если боковые ребра перпендикулярны к основаниям, то
призма называется прямой, в противном случае наклонной.
Высота прямой призмы равна ее боковому ребру.

28.

Прямая призма называется правильной, если ее основания
- правильные многоугольники. У такой призмы все боковые
грани – равные прямоугольники.

29.

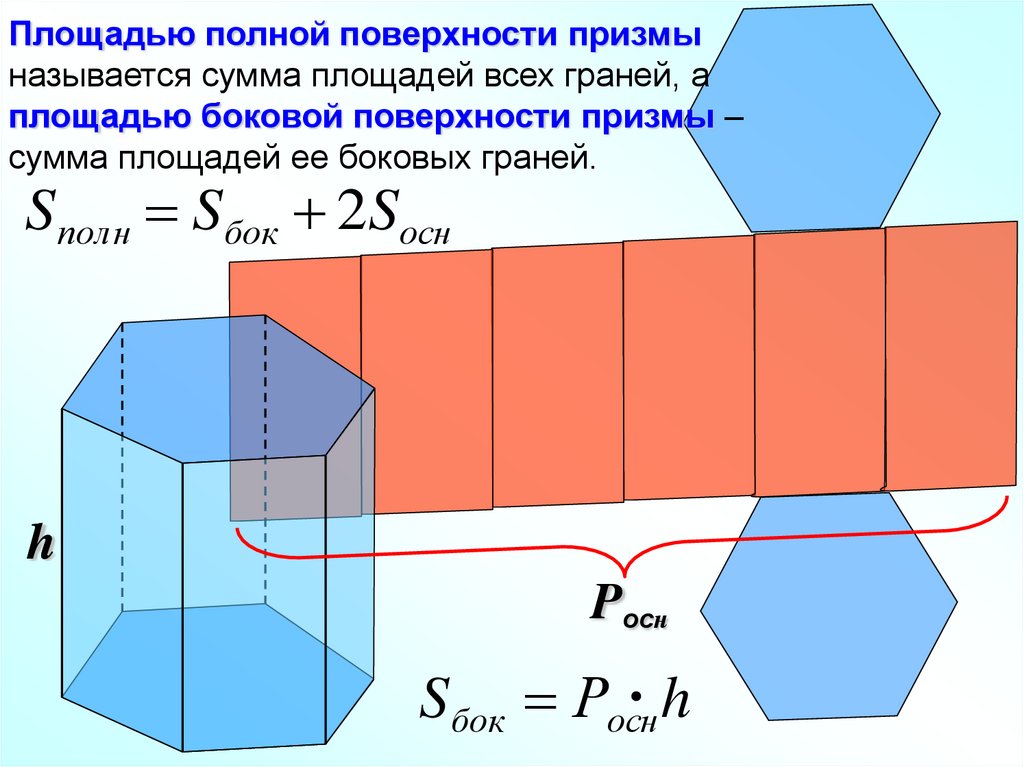
Площадью полной поверхности призмы
называется сумма площадей всех граней, а
площадью боковой поверхности призмы –
сумма площадей ее боковых граней.
Sполн Sбок 2Sосн
h
Pocн
Sбок Росн h

30.

Параллельная проекция призмы.
Для того чтобы построить параллельную проекцию
призмы, достаточно построить многоугольник, изображающий ее основание. Затем из вершин многоугольника
провести прямые, параллельные некоторой фиксированной прямой, и отложить на них равные отрезки. Соединяя
концы этих отрезков, получим многоугольник, являющийся изображением второго основания призмы.