Цилиндр. Шар. Задачи по геометрии

1.

Задачи по геометрии
Цилиндр.
Шар
1

2.

Площади и объем цилиндра.
Решение задач.
2

3.

№1 Найдите объем и площадь боковой
поверхности тела, полученного при вращении
прямоугольника со сторонами 6 и 8 см вокруг
прямой, которая проходит через середины его
меньших сторон.
6
8
Дано:
ABCD – прямоугольник
вращается вокруг оси
симметрии меньших сторон,
образуется цилиндр высокий.
AB = 6 см, BC = 8 см.
Найти: V цилиндра , S бок. цилиндра
3

4.

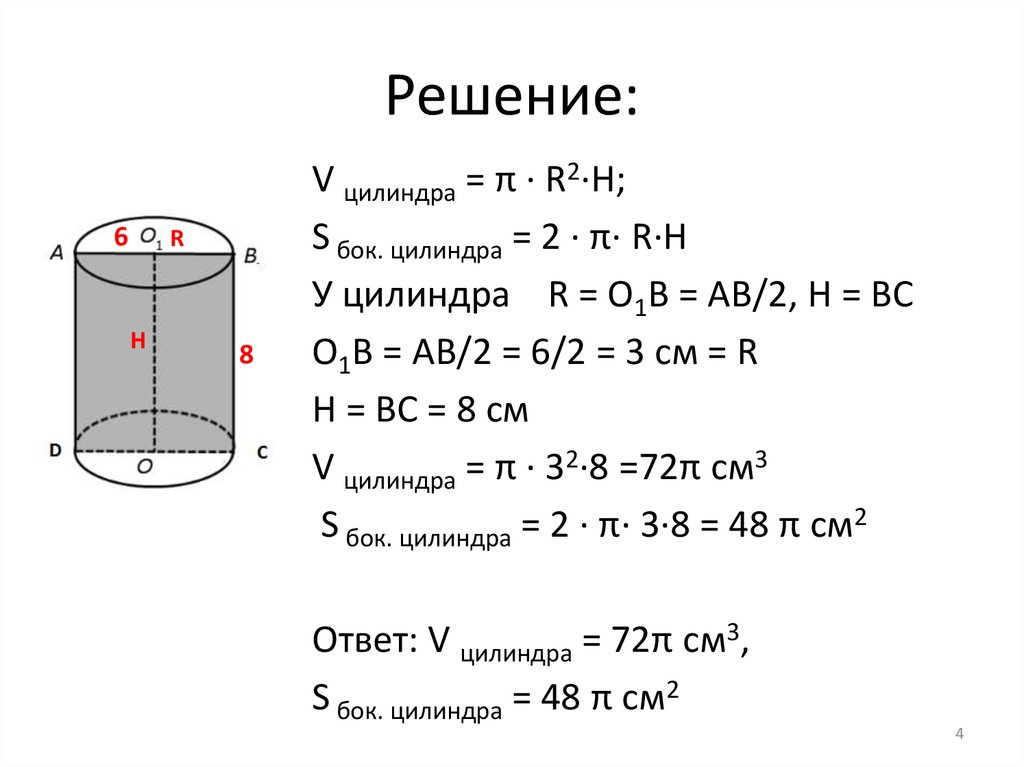
Решение:
6
R
H
8
V цилиндра = π · R2·H;
S бок. цилиндра = 2 · π· R·H
У цилиндра R = O1B = AB/2, H = BC
O1B = AB/2 = 6/2 = 3 см = R
H = BC = 8 см
V цилиндра = π · 32·8 =72π см3
S бок. цилиндра = 2 · π· 3·8 = 48 π см2
Ответ: V цилиндра = 72π см3,
S бок. цилиндра = 48 π см2
4

5.

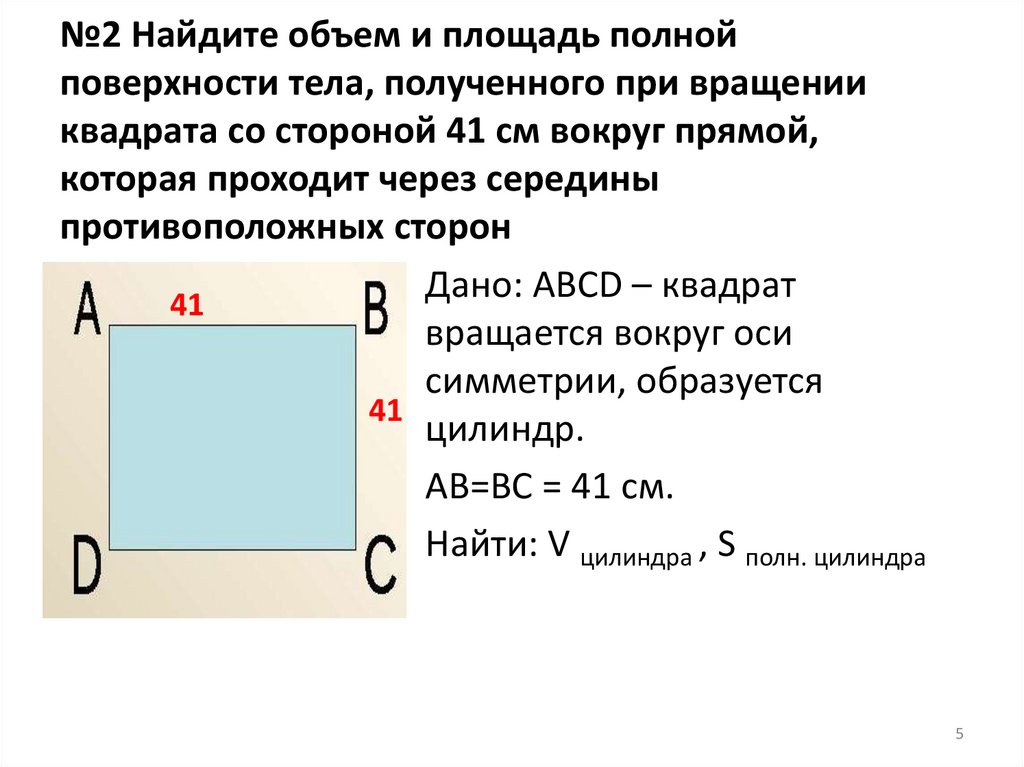
№2 Найдите объем и площадь полной
поверхности тела, полученного при вращении
квадрата со стороной 41 см вокруг прямой,
которая проходит через середины
противоположных сторон
Дано: ABCD – квадрат
41
вращается вокруг оси
симметрии, образуется
41
цилиндр.
AB=ВС = 41 см.
Найти: V цилиндра , S полн. цилиндра
5

6.

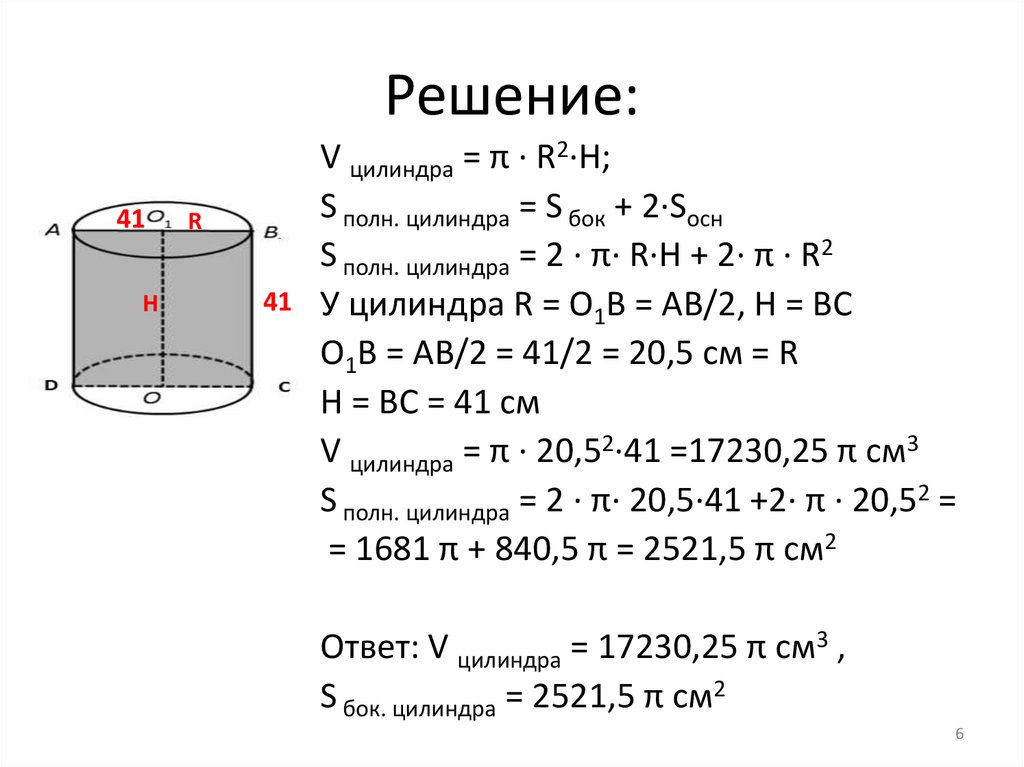
Решение:
41
H
R
41
V цилиндра = π · R2·H;
S полн. цилиндра = S бок + 2·Sосн
S полн. цилиндра = 2 · π· R·H + 2· π · R2
У цилиндра R = O1B = AB/2, H = BC
O1B = AB/2 = 41/2 = 20,5 см = R
H = BC = 41 см
V цилиндра = π · 20,52·41 =17230,25 π см3
S полн. цилиндра = 2 · π· 20,5·41 +2· π · 20,52 =
= 1681 π + 840,5 π = 2521,5 π см2
Ответ: V цилиндра = 17230,25 π см3 ,
S бок. цилиндра = 2521,5 π см2
6

7.

Практическая работа
Вариант В=20
В – 2 последние цифры по студенческому билету
№1 Найдите объем и
площадь полной
поверхности тела,
полученного при
вращении
прямоугольника со
сторонами 10 и В см
вокруг прямой, которая
проходит через середины
его больших сторон.
№2 Найдите объем и
площадь боковой
поверхности тела,
полученного при
вращении квадрата со
стороной В0 см вокруг
прямой, которая проходит
через середины
противоположных сторон
7

8.

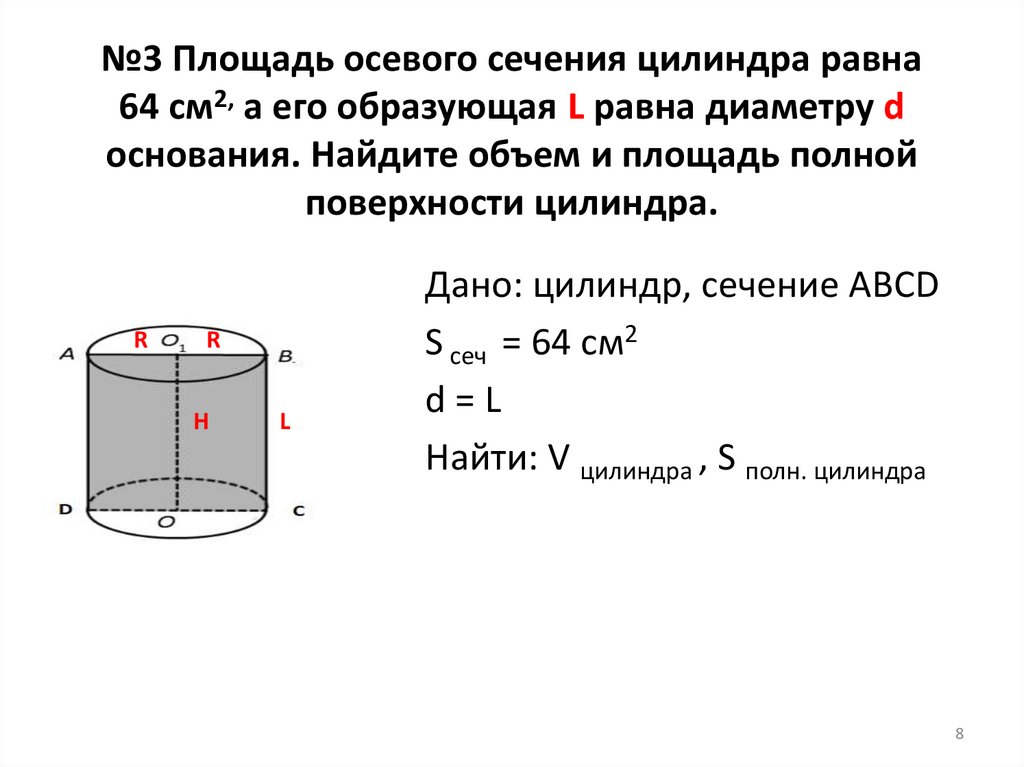
№3 Площадь осевого сечения цилиндра равна
64 см2, а его образующая L равна диаметру d
основания. Найдите объем и площадь полной
поверхности цилиндра.
R
R
Н
L
Дано: цилиндр, сечение ABCD
S сеч = 64 см2
d=L
Найти: V цилиндра , S полн. цилиндра
8

9.

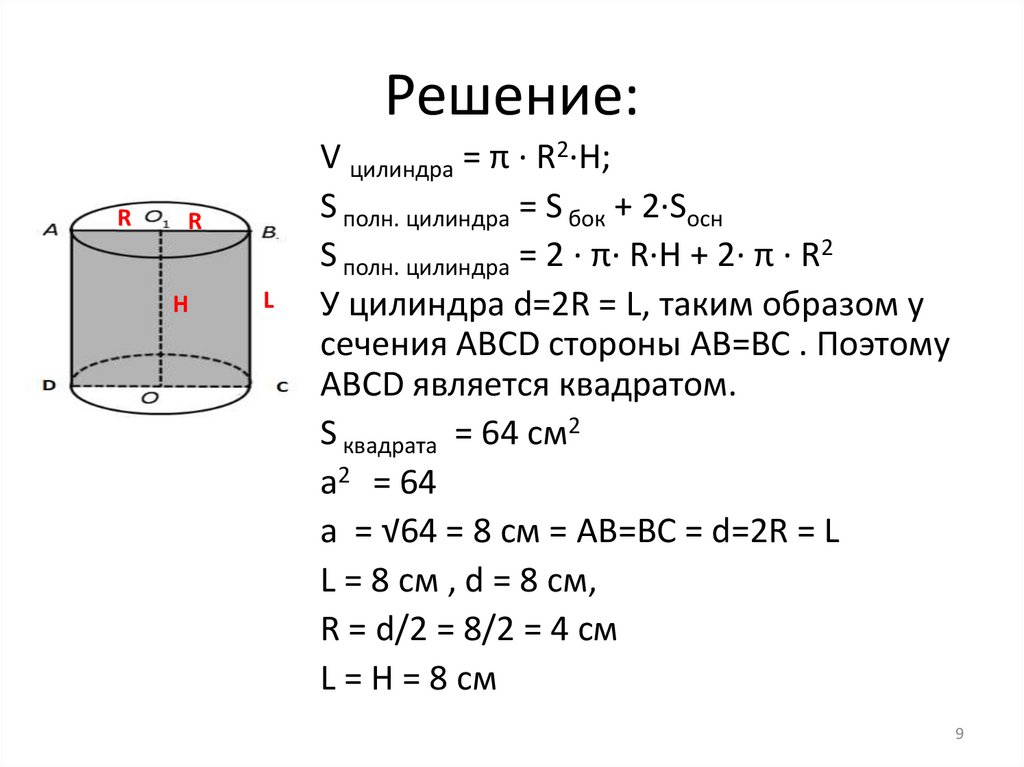
Решение:
R
R
H
L
V цилиндра = π · R2·H;
S полн. цилиндра = S бок + 2·Sосн
S полн. цилиндра = 2 · π· R·H + 2· π · R2
У цилиндра d=2R = L, таким образом у
сечения АВСD стороны АВ=ВС . Поэтому
АВСD является квадратом.
S квадрата = 64 см2
a2 = 64
a = √64 = 8 см = АВ=ВС = d=2R = L
L = 8 см , d = 8 см,
R = d/2 = 8/2 = 4 см
L = Н = 8 см
9

10.

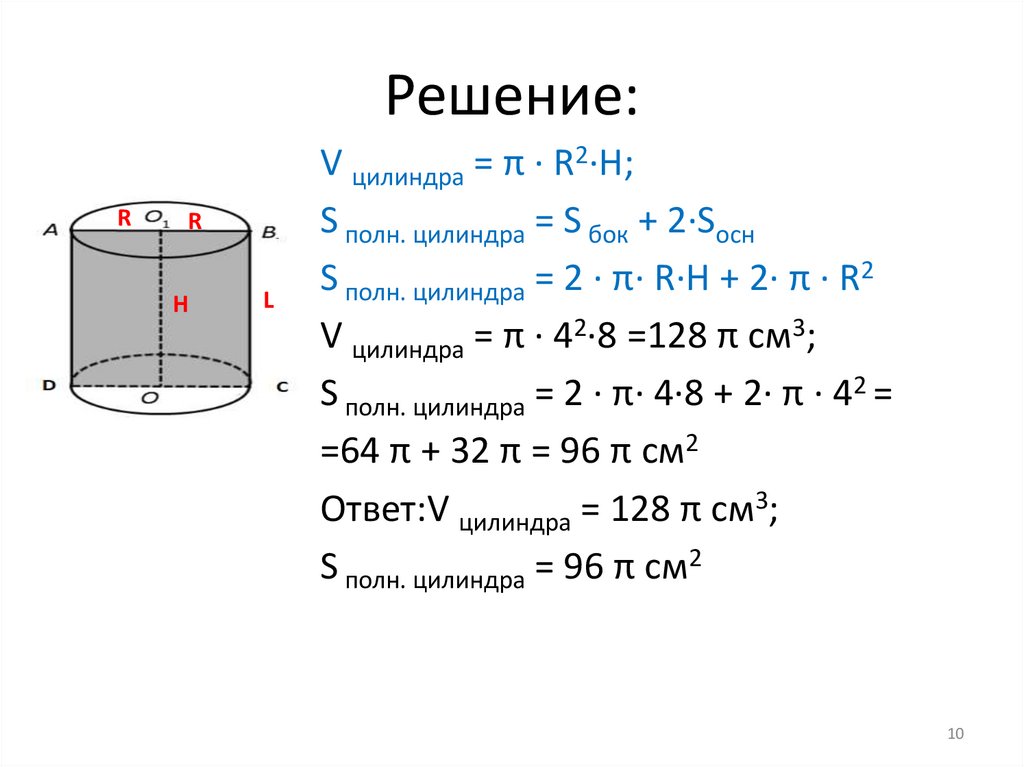
Решение:
R
R
H
L
V цилиндра = π · R2·H;
S полн. цилиндра = S бок + 2·Sосн
S полн. цилиндра = 2 · π· R·H + 2· π · R2
V цилиндра = π · 42·8 =128 π см3;
S полн. цилиндра = 2 · π· 4·8 + 2· π · 42 =
=64 π + 32 π = 96 π см2
Ответ:V цилиндра = 128 π см3;
S полн. цилиндра = 96 π см2
10

11.

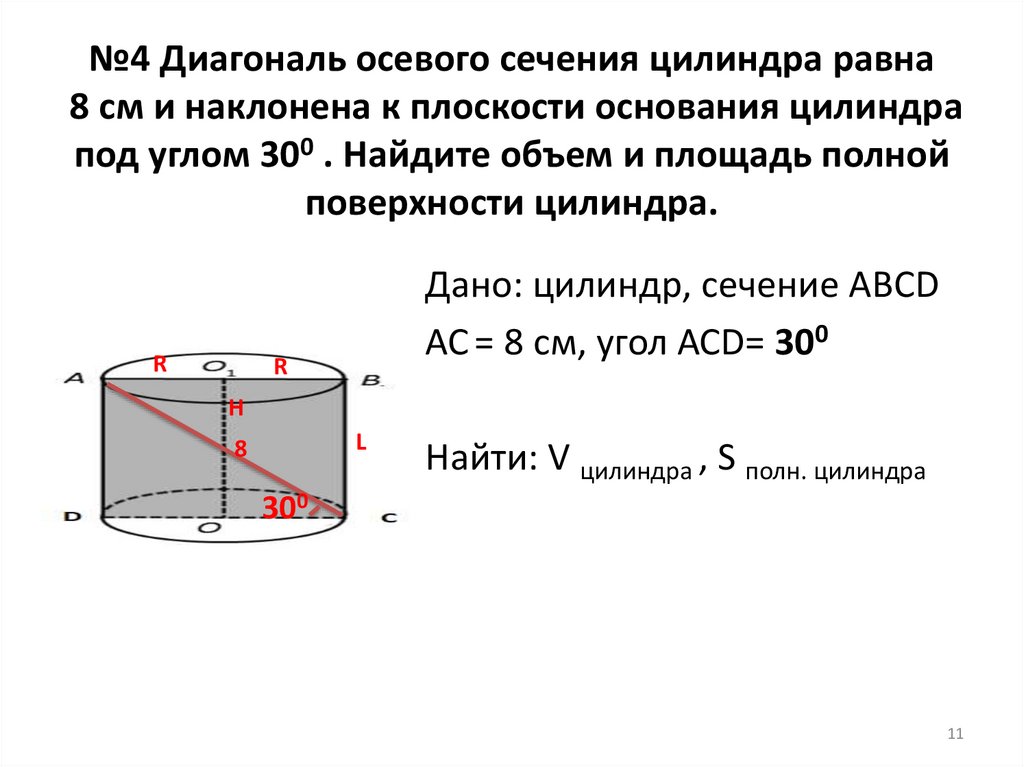
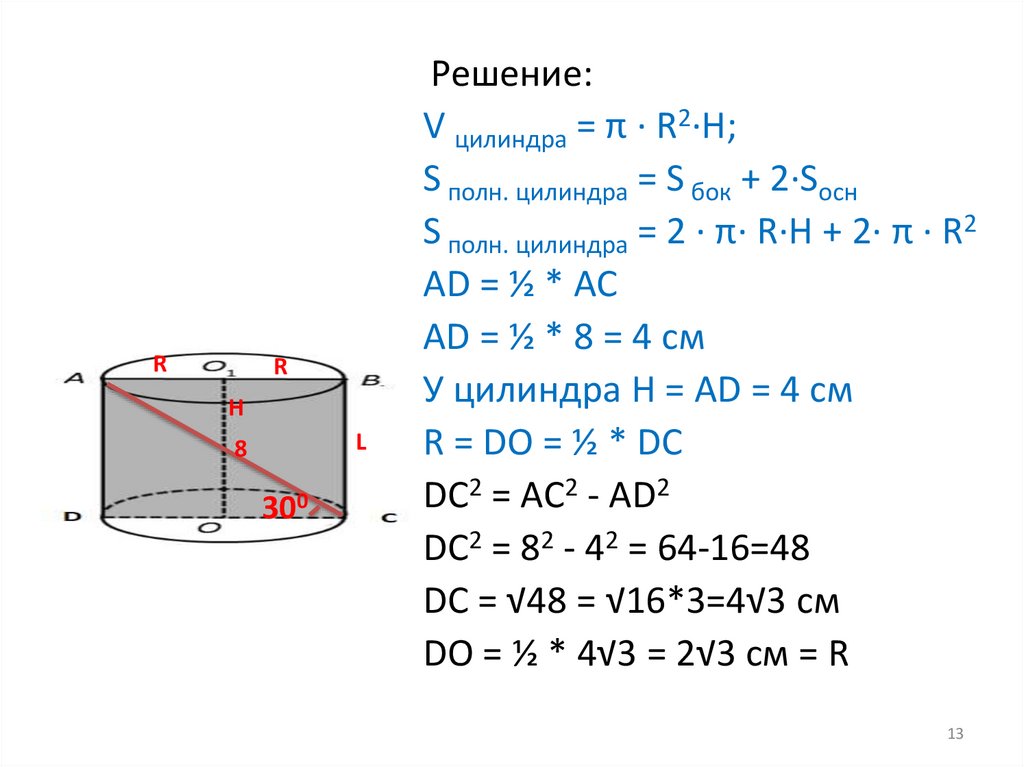
№4 Диагональ осевого сечения цилиндра равна
8 см и наклонена к плоскости основания цилиндра
под углом 300 . Найдите объем и площадь полной
поверхности цилиндра.
R
Дано: цилиндр, сечение ABCD
АС = 8 см, угол АСD= 300
R
Н
L
8
Найти: V цилиндра , S полн. цилиндра
300
11

12.

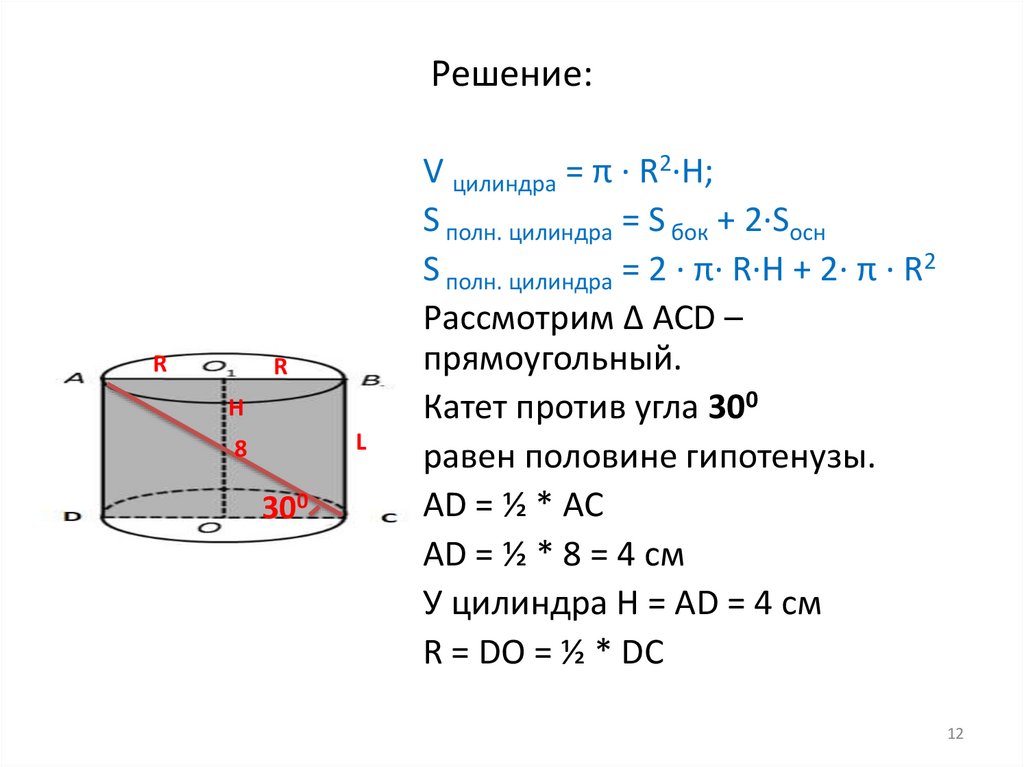
Решение:
R
R
Н
L
8
300
V цилиндра = π · R2·H;
S полн. цилиндра = S бок + 2·Sосн
S полн. цилиндра = 2 · π· R·H + 2· π · R2
Рассмотрим ∆ ACD –
прямоугольный.
Катет против угла 300
равен половине гипотенузы.
AD = ½ * AC
AD = ½ * 8 = 4 cм
У цилиндра H = AD = 4 cм
R = DO = ½ * DC
12

13.

R
R
Н
L
8
300
Решение:
V цилиндра = π · R2·H;
S полн. цилиндра = S бок + 2·Sосн
S полн. цилиндра = 2 · π· R·H + 2· π · R2
AD = ½ * AC
AD = ½ * 8 = 4 cм
У цилиндра H = AD = 4 cм
R = DO = ½ * DC
DC2 = AC2 - AD2
DC2 = 82 - 42 = 64-16=48
DC = √48 = √16*3=4√3 см
DO = ½ * 4√3 = 2√3 см = R
13

14.

Решение:
V цилиндра = π · R2·H;
S полн. цилиндра = S бок + 2·Sосн
S полн. цилиндра = 2 · π· R·H + 2· π · R2
У цилиндра H = AD = 4 cм
DO = ½ * 4√3 = 2√3 см = R
R
R
Н
L
8
300
V цилиндра = π · (2√3) 2·4 = π · (4 · 3) ·4 =
=48 π см3
S полн. цилиндра =
2 · π· (2√3) ·4 + 2· π · (2√3) 2 =
=16 √3 π + 2· π · 4 ·3 = 16 √3 π +24 π
см2
Ответ: V цилиндра = 48 π см3
S полн. цилиндра = 16 √3 π +24 π см2
14

15.

Самостоятельная работа
Вариант В=20
№3
Площадь осевого сечения
цилиндра равна
В см2, а его образующая
равна диаметру
основания. Найдите
объем и площадь полной
поверхности цилиндра.
№4
Диагональ осевого
сечения цилиндра равна
В*2 см и наклонена к
плоскости основания
цилиндра под углом 300 .
Найдите объем и
площадь полной
поверхности цилиндра.
15

16.

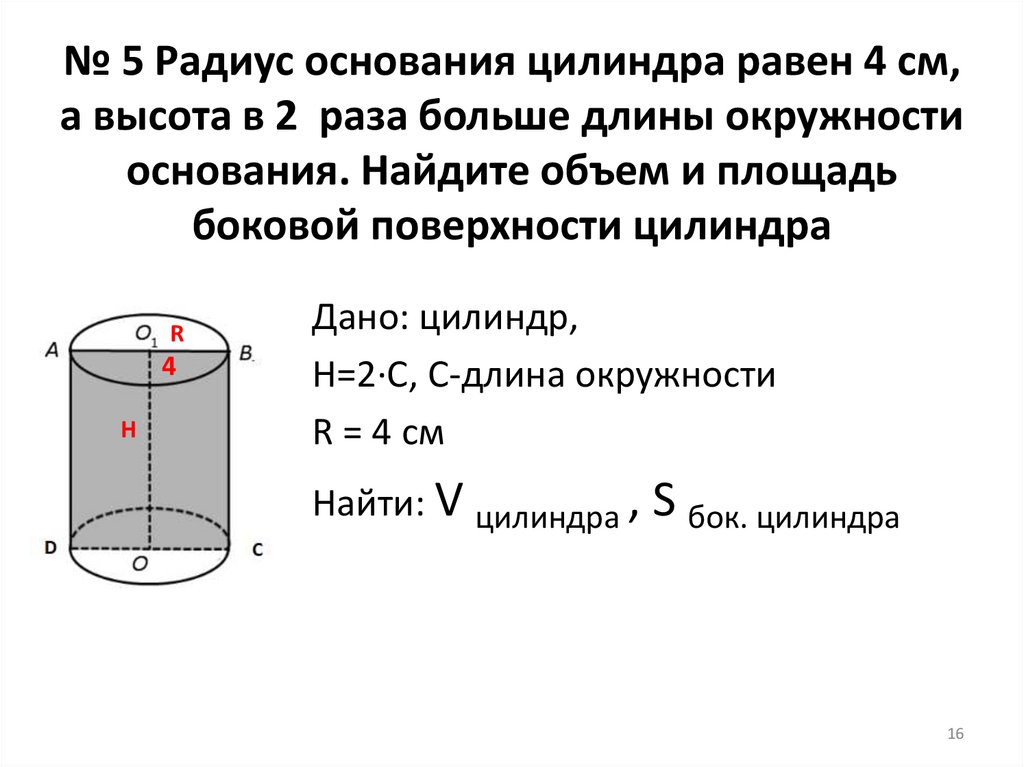
№ 5 Радиус основания цилиндра равен 4 см,
а высота в 2 раза больше длины окружности
основания. Найдите объем и площадь
боковой поверхности цилиндра
R
4
H
Дано: цилиндр,
Н=2·С, С-длина окружности
R = 4 см
Найти: V цилиндра , S бок. цилиндра
16

17.

R
4
H
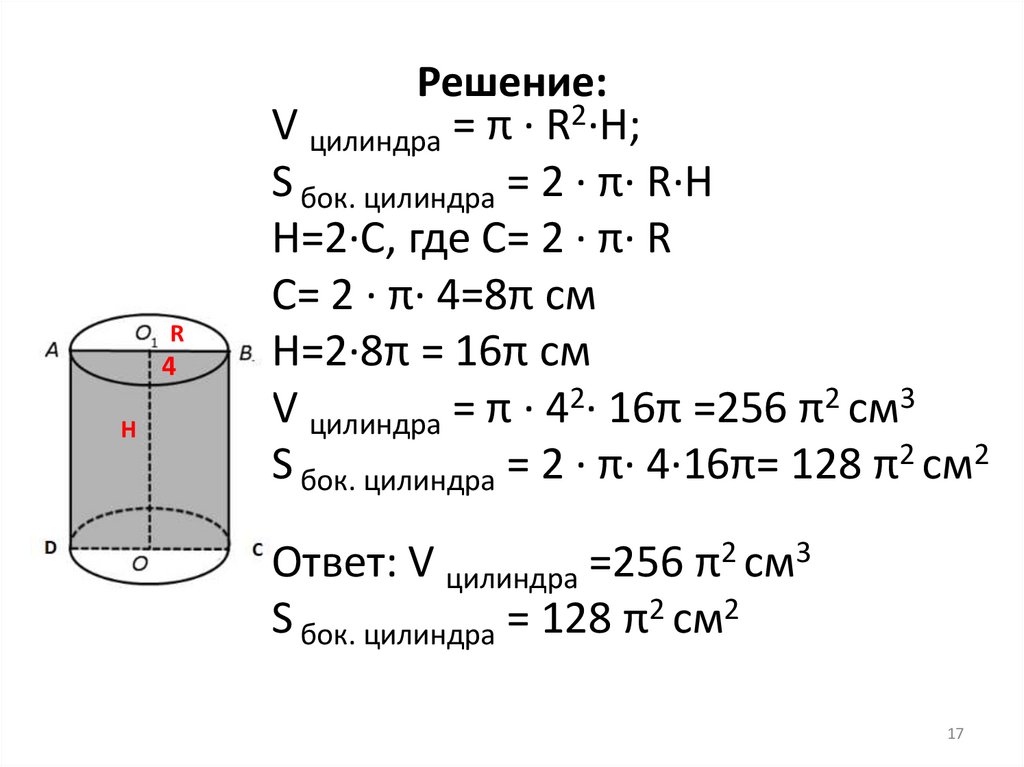
Решение:
V цилиндра = π · R2·H;
S бок. цилиндра = 2 · π· R·H
Н=2·С, где С= 2 · π· R
С= 2 · π· 4=8π см
Н=2·8π = 16π см
V цилиндра = π · 42· 16π =256 π2 см3
S бок. цилиндра = 2 · π· 4·16π= 128 π2 см2
Ответ: V цилиндра =256 π2 см3
S бок. цилиндра = 128 π2 см2
17

18.

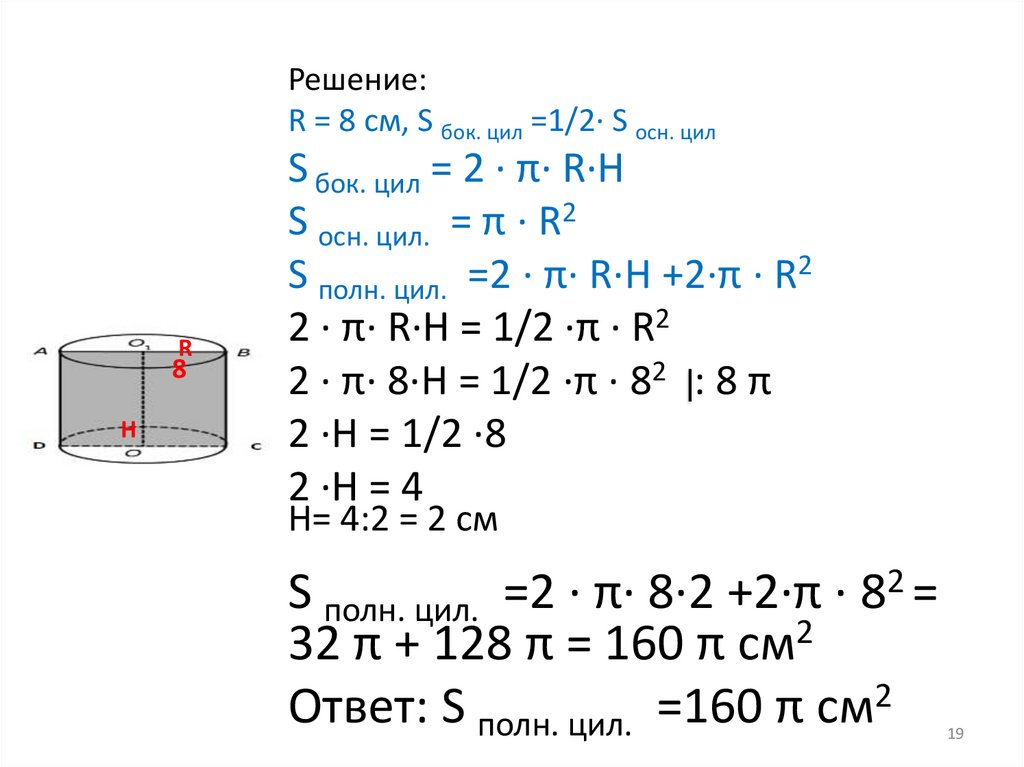
№ 6 Радиус основания цилиндра равен 8 см,
площадь боковой поверхности вдвое меньше
площади основания. Найдите площадь полной
поверхности цилиндра
R
8
H
Дано: цилиндр
R = 8 см, S бок. цил =1/2· S осн. цил
Найти: S полн. цилиндра
Решение:
S бок. цил = 2 · π· R·H
S осн. цил. = π · R2
S полн. цил. =2 · π· R·H +2·π · R2
18

19.

Решение:
R = 8 см, S бок. цил =1/2· S осн. цил
R
8
H
S бок. цил = 2 · π· R·H
S осн. цил. = π · R2
S полн. цил. =2 · π· R·H +2·π · R2
2 · π· R·H = 1/2 ·π · R2
2 · π· 8·H = 1/2 ·π · 82 : 8 π
2 ·H = 1/2 ·8
2 ·H = 4
Н= 4:2 = 2 см
S полн. цил. =2 · π· 8·2 +2·π · 82 =
32 π + 128 π = 160 π см2
Ответ: S полн. цил. =160 π см2
19

20.

Вариант В=20
№ 5 Радиус основания
цилиндра равен В0 см, а
высота в 2 раза меньше
длины окружности
основания. Найдите
объем и площадь
боковой поверхности
цилиндра
№ 6 Радиус основания
цилиндра равен В см,
площадь боковой
поверхности вдвое
больше площади
основания. Найдите
площадь полной
поверхности цилиндра
20

21.

Площадь и объем шара.
Площадь сечения шара.
Решение задач.
21

22.

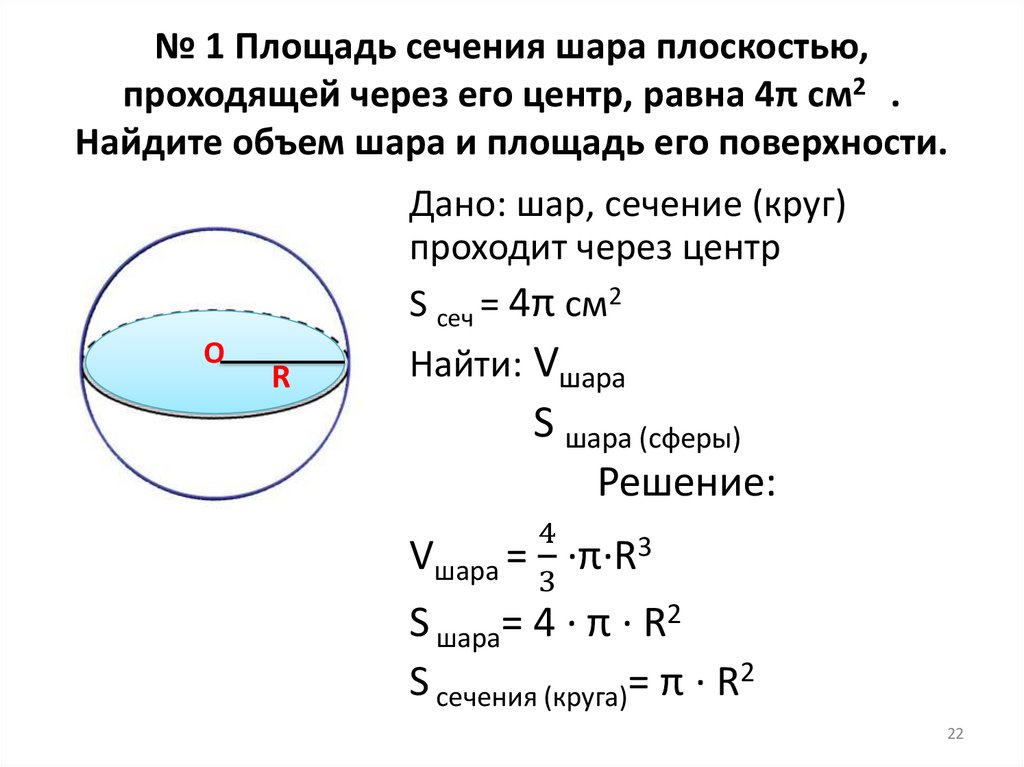
№ 1 Площадь сечения шара плоскостью,
проходящей через его центр, равна 4π см2 .
Найдите объем шара и площадь его поверхности.
Дано: шар, сечение (круг)
проходит через центр
S сеч = 4π см2
О
R
Найти: Vшара
S шара (сферы)
Решение:
4
3
Vшара = ·π·R3
S шара= 4 · π · R2
S сечения (круга)= π · R2
22

23.

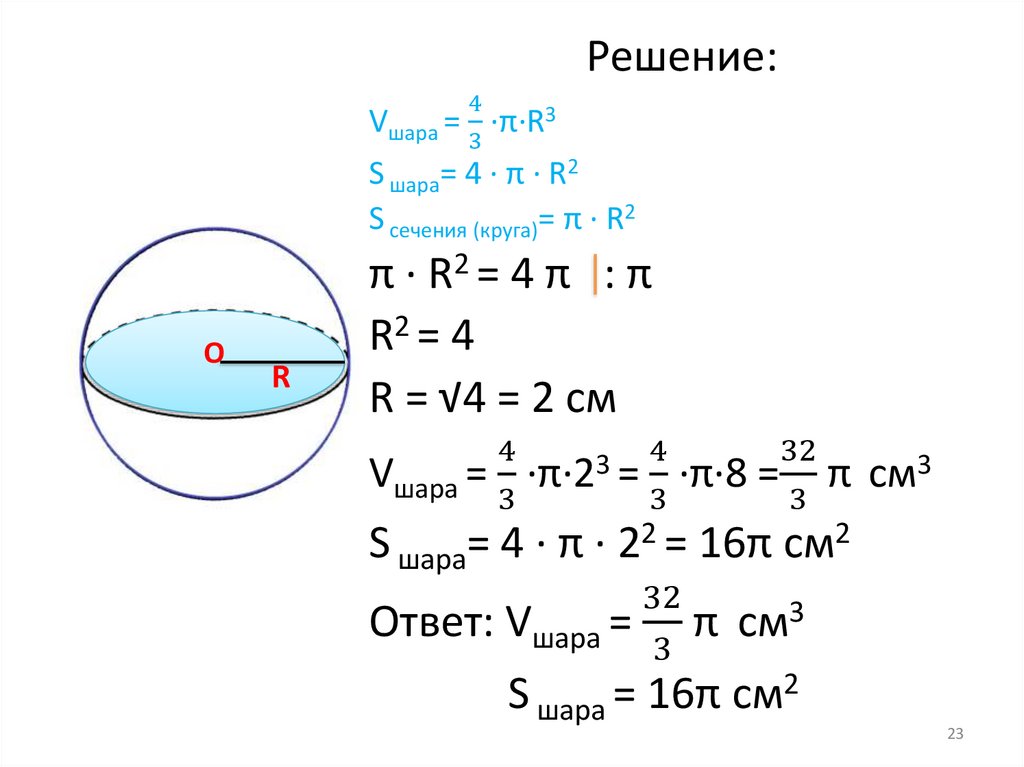
Решение:
4
3
Vшара = ·π·R3
S шара= 4 · π · R2
S сечения (круга)= π · R2
О
R
π · R2 = 4 π : π
R2 = 4
R = √4 = 2 см
Vшара =
4
3
4
3
·π·2 =
S шара= 4 · π ·
·π·8
3
22 =
Ответ: Vшара =
32
3
32
=
3
π см3
16π см2
π см3
S шара = 16π см2
23

24.

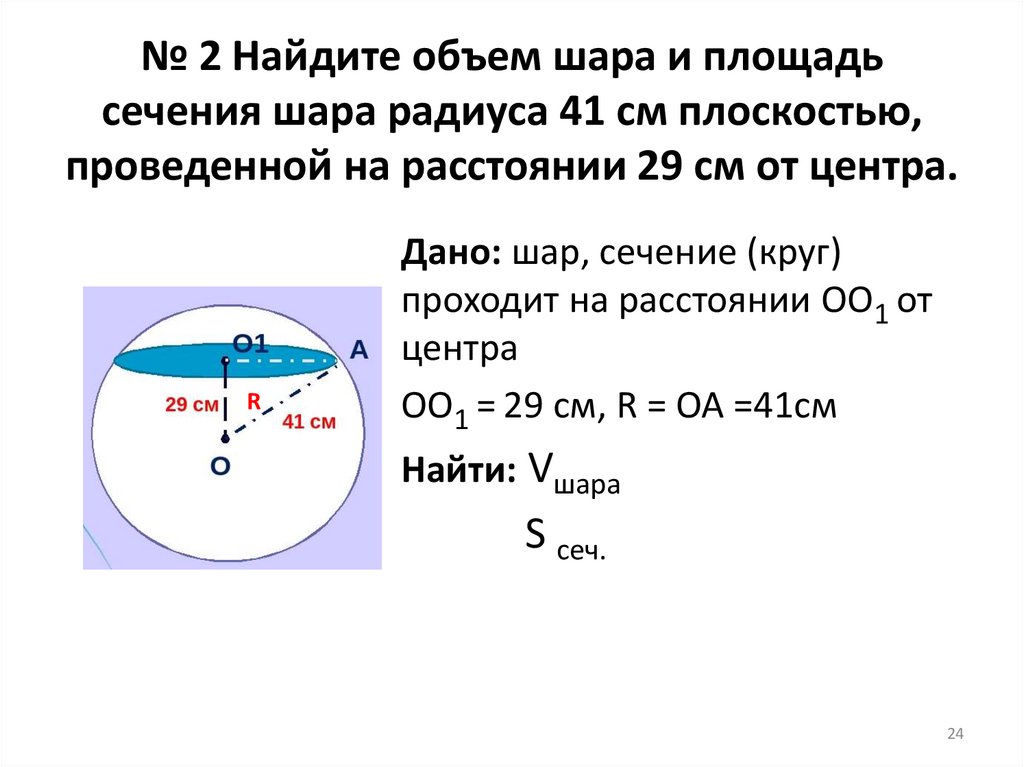
№ 2 Найдите объем шара и площадь
сечения шара радиуса 41 см плоскостью,
проведенной на расстоянии 29 см от центра.
R
Дано: шар, сечение (круг)
проходит на расстоянии OO1 от
центра
OO1 = 29 см, R = ОА =41см
Найти: Vшара
S сеч.
24

25.

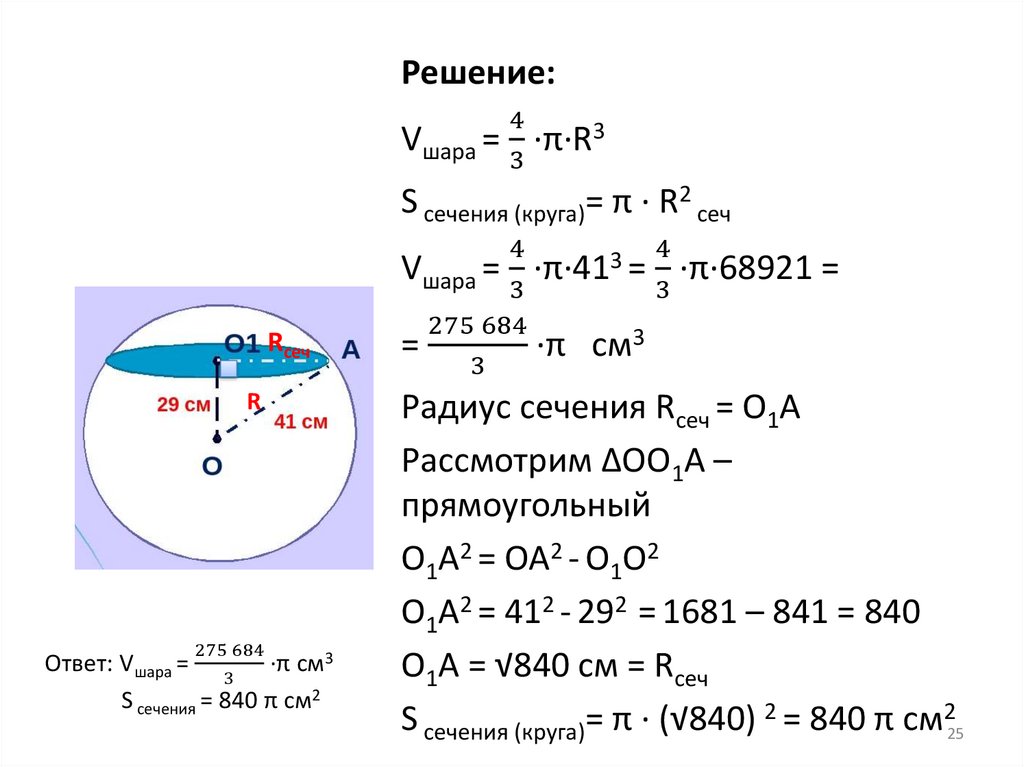
Решение:
4
3
Vшара = ·π·R3
S сечения (круга)= π · R2 сеч
Rсеч
R
275 684
Ответ: Vшара = 3 ·π см3
S сечения = 840 π см2
4
4
3
Vшара = ·π·41 =
3
3
275 684
=
·π см3
3
·π·68921 =
Радиус сечения Rсеч = O1A
Рассмотрим ∆OO1A –
прямоугольный
O1A2 = OA2 - O1О2
O1A2 = 412 - 292 = 1681 – 841 = 840
O1A = √840 см = Rсеч
S сечения (круга)= π · (√840) 2 = 840 π см225

26.

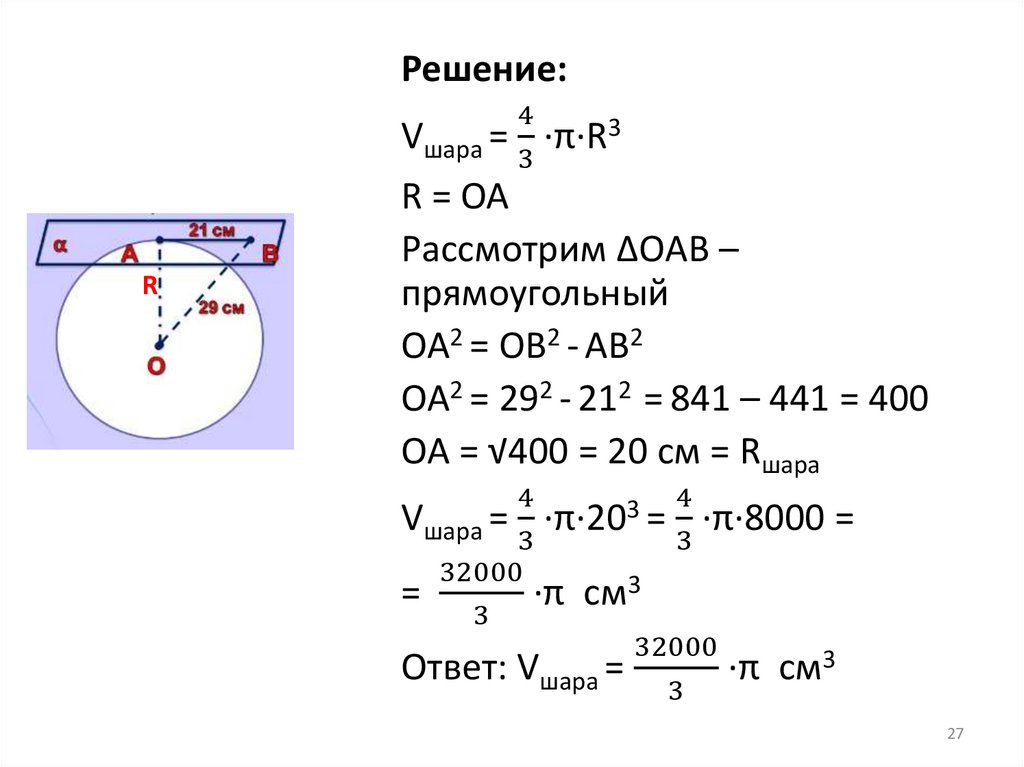
№ 3 Шар с центром в точке О касается плоскости в
точке А. Точка В лежит в плоскости касания.
Найдите объем шара, если АВ=21 см, ВО = 29 см.
R
Дано: шар,
плоскость касания проходит на
расстоянии OА от центра,
точка В лежит в плоскости
касания
АВ = 21 см, R = ОА, ВО=29 см
Найти: Vшара
26

27.

Решение:
4
3
Vшара = ·π·R3
R
R
R = ОА
Рассмотрим ∆OAВ –
прямоугольный
OA2 = OВ2 - АВ2
OA2 = 292 - 212 = 841 – 441 = 400
OA = √400 = 20 см = Rшара
4
4
3
Vшара = ·π·20 = ·π·8000 =
3
3
32000
=
·π см3
3
32000
Ответ: Vшара =
·π см3
3
27

28.

Самостоятельная работа
Вариант В= 5, № =3
№ 1 Площадь сечения шара плоскостью,
проходящей через его центр, равна Вπ см2 .
Найдите объем шара и площадь его
поверхности.
№ 2 Найдите объем шара и площадь сечения
шара радиуса В0 см плоскостью, проведенной
на расстоянии № см от центра.
№ 3 Шар с центром в точке О касается плоскости
в точке А. Точка В лежит в плоскости касания.
Найдите объем шара, если АВ=№ см, ВО = В см.
28