Декартові координати

1.

2.

Активізація опорних знань
Для цього вченого самою зрозумілою
і точною мовою для вираження
наукових істин була мова
математики
Рене Декарт (1596 1650) – французький
математик
створив прямокутну
систему координат

3.

Дека́ртова систе́ма координа́т (або прямоку́тна
систе́ма координа́т, англ. Cartesian coordinate system) —
система координат, яка дозволяє однозначним чином
визначити кожну точку на площині за допомогою
пари числових координа́т, які
задають знакові відстані до точки відносно двох
визначених перпендикулярно спрямованих прямих,
що задано в однакових одиницях довжини. Кожна
така пряма, від якої відкладається відстань,
називається віссю координат (англ. coordinate axis) або
просто віссю системи, а точка, де вони перетинаються,
називається початком координат, що має
впорядковану пару координат (0, 0). Декартову
систему координат вперше запропонував
відомий французький математик Рене
Декарт близько 1637 року в праці «Геометрія»,
одному з додатків до видатного філософського
твору «Міркування про метод».

4.

Декартова система координат
у
4
3
2
-5 -4 -3 -2 -1
1
0
1 2 3 4 5
-1
-2
-3
-4
х
Декартова система
координат на
площині задається двома
взаємно
перпендикулярними
осями (вісь ОХ – вісь
абсцис, вісь ОУ – вісь
ординат), які мають
спільний
початок О (початок
координат) і однаковий
масштаб осей.

5.

-II+
X<0,y>0
+I+
x>0,y>0
-III-
+IV-
X<0,y<0
x>0,y<0

6.

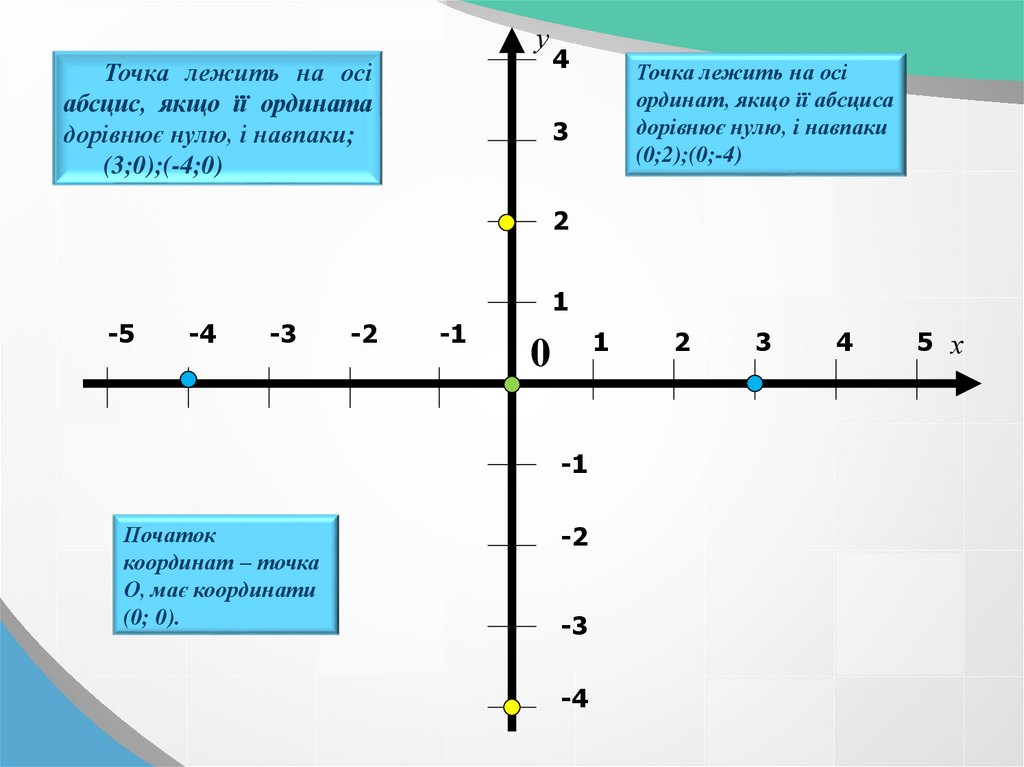
у
Точка лежить на осі
абсцис, якщо її ордината
дорівнює нулю, і навпаки;
(3;0);(-4;0)
4
Точка лежить на осі
ординат, якщо її абсциса
дорівнює нулю, і навпаки
(0;2);(0;-4)
3
2
1
-5
-4
-3
-2
-1
1
0
-1
Початок
координат – точка
О, має координати
(0; 0).
-2
-3
-4
2
3
4
5 х

7.

У
5
В
А
4
3
К
Р
2
1
R
-5 -4 -3 -2 0 -1 1
-1
5
-2
-3
M
E
-4
-5
Д
С
Х
2
3
4
F
G
А(3;4)
В(-3;4)
С(2;0)
Д(4;2)
К(-1;1)
Р(0;1)
R(-3;0)
М(-1;-4)
Е(0;-4)
G(2;-4)
F(5;-3)

8.

У
y2
А
М
y0
В
y1
0
A1
M1
x1 x0
B1
x2
x1 x2
y1 y2
x0
, y0
2
2
Х

9.

Координат и середини відрізка
Кожна координата середини відрізка
дорівнює
півсумі відповідних координат його кінців.
х1 х 2
х0
2
y1 y 2
у0
2
Нехай відрізок АВ
має кінці А(х1; у1) і В(х2; у2)
і нехай М(х0; у0) — середина
відрізка АВ
MD — середня лінія
трапеції з основами х1 і х2,
МС — середня лінія трапеції
з основами у1 і у2.
За властивістю середньої
лінії трапеції
маємо дані формули

10.

У
5
4
3
А
2
М1
-7
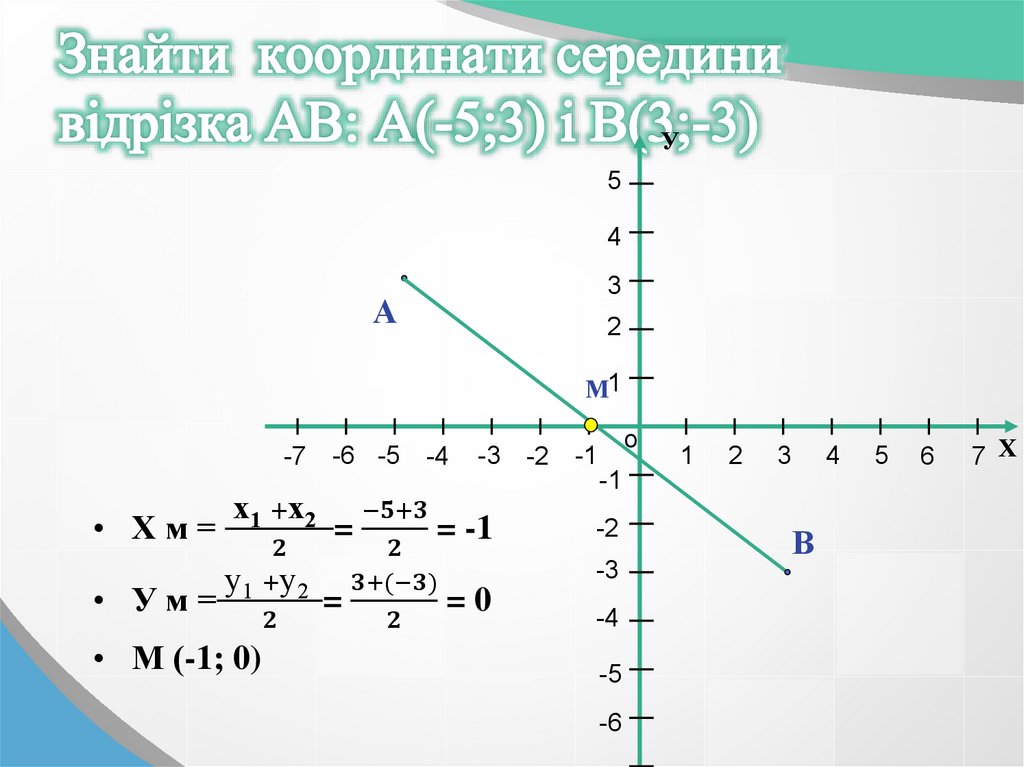
• Хм=
• Ум=
х1 +х2