Похожие презентации:
Прямокутна система координат в просторі
1.
Рівень стандарту.2.
Рене Декарт1596-1650 р
Французький філософ,
математик. Один із
засновників аналітичної
геометрії. Ввів поняття
змінної величини. Один із
перших розглянув
координатну площину та
описав метод координат в
своїх працях “Геометрія” та
“Міркування про метод”.
Вчесть вченого названа
координатна площина.
3.
4.
5.
ПРЯМОКУТНА СИСТЕМА КООРДИНАТ ВПРОСТОРІ
z
0
xy
x
xz
yz
y
x, y , z
- три
координатні
попарно
перпендикулярні
прямі
xy, yz , xz - три
координатні
попарно
перпендикулярні
площини
6. Координати точки та її проекції на координатні прямі та площини
вісьаплікат
z
Аz
Аyz
Аxz
Аx
вісь абсцис
x
А
0
вісь
ординат
Аy
y
Аxy
7.
8. Побудуйте точку за її координатами
А(2;3;1)z
1
0
А
2
x
3
y
9.
Побудуйте точку за їїкоординатами
C(0;2;-3)
z
0
2
y
x
3
С
10. Проекції точки на координатні прямі та площини
AxAy
Az
Axz
Ayz
Axy
проекції точки на координатні прямі
абсциса, ордината,
апліката
проекції точки на координатні
площини
11. Проекції точки на координатні прямі та площини
AxAy
Az
Axy
Axz
Ayz
(x;0;0)
(0; y ;0)
(0;0; z )
( x; y;0)
( x;0; z )
(0; y; z )
12.
13.
ПІД ЯКИМКУТОМ
ПЕРЕТИНАЮТ
ЬСЯ
КООРДИНАТНІ
ПРЯМІ
У ПРОСТОРІ:
А) ПІД ГОСТРИМ
КУТОМ;
Б) ПІД ПРЯМИМ
КУТОМ;
В) ПІД ТУПИМ КУТОМ;
Г) ПІД РОЗГОРНУТИМ
КУТОМ
ЯК
НАЗИВАЮТЬ
ТОЧКУ
ПЕРЕТИНУ
КООРДИНАТНИ
Х
ПРЯМИХ:
А) НУЛЬ;
Б) СЕРЕДИНА;
В) ПОЧАТОК
КООРДИНАТ;
Г) ТОЧКА ВІДЛІКУ
ЯК
НАЗИВАЮТЬС
Я
(Х; У; Z)
ДЛЯ ТОЧКИ
У ПРОСТОРІ:
А) КООРДИНАТИ
ТОЧКИ;
Б) ЧИСЛА
У ПРОСТОРІ;
В) ЧИСЛА
ДЛЯ ТОЧКИ;
Г) ПОКАЗНИКИ
ТОЧКИ
14.
ЯКНАЗИВАЕТЬСЯ
ВІСЬ ОХ:
ЯК
НАЗИВАЕТЬСЯ
ВІСЬ ОУ:
А) АПЛІКАТА;
Б) ОРДИНАТА;
В) АБСЦИСА;
Г) ПОЧАТОК
А) ОРДИНАТА;
Б) АБСЦИСА;
В) ПОЧАТОК;
Г) АПЛІКАТА
ЯК
НАЗИВАЕТЬС
Я
ВІСЬ ОZ :
А) АБСЦИСА;
Б) АПЛІКАТА;
В) ОРДИНАТА;
Г) ПОЧАТОК
15.
ЯКЩО ТОЧКАНАЛЕЖИТЬ
ОСІ ОХ,
ТО ЇЇ
КООРДИНАТИ:
А) ( О; У; О);
Б) (О; О; Z);
В) (Х; О; О);
ЯКЩО ТОЧКА
НАЛЕЖИТЬ
ОСІ ОУ,
ТО ЇЇ
КООРДИНАТИ:
А) ( О; У; О);
Б) (О; О; Z);
В) (Х; О; О);
ЯКЩО ТОЧКА
НАЛЕЖИТЬ
ОСІ ОZ,
ТО ЇЇ
КООРДИНАТИ
:
А) ( О; У; О);
Б) (О; О; Z);
В) (Х; О; О);
16.
НАЛЕЖАТЬ ОСІ ОХНАЛЕЖАТЬ ПЛОСКОСТІ ХУ
НАЛЕЖАТЬ ПЛОСКОСТІ ХZ
НАЛЕЖАТЬ ПЛОСКОСТІ УZ
НАЛЕЖАТЬ ОСІ ОZ
НАЛЕЖАТЬ ОСІ ОУ
ЗНАХОДЯТЬСЯ У ПРОСТОРІ
17. ВІДСТАНЬ МІЖ ДВОМА ТОЧКАМИ НА ПЛОЩИНІ
ВІДСТАНЬ МІЖ ДВОМА ТОЧКАМИУ НА ПЛОЩИНІ
6
5
у₂
3
2
у₁
-7
-6 -5
-4
-3
-2
В (х₂;у₂)
4
А (х₁;у₁)
1
С
о
-1
-1
-2
-3
-4
-5
-6
-7
1
2
х₁
3
4
5
х₂
6
7 Х
18.
ВІДСТАНЬ МІЖ ДВОМА ТОЧКАМИ В ПРОСТОРІz
z2
A( x1, y1, z1 )
B( x2 , y2 , z2 )
B
z1
x1
x2
x
АВ
A
y2
y1
o
y
A0
B0
( х2 х1 ) 2 ( у2 у1 ) 2 ( z2 z1 ) 2
19.
НА КООРДИНАТНІЙПРЯМІЙ
С
A
х А хВ
хС
2
В
ХА
ХВ
НА КООРДИНАТНІЙ
ПЛОЩИНІ
A
у
В
z
АВ Х В Х А
х А хВ
хС
АВ х х у у
2
В
у А уВ
уС
х
2
А
2
В
А
х А хВ
В хВ уВ zВ хС
2
У ПРОСТОРІ
С Х С ;У С ; ZC
А хА уА z А х
у
ВІДСТАНЬ МІЖ
ДВОМА ТОЧКАМИ
2
С
о
КООРДИНАТИ
СЕРЕДИНИ
ВІДРІЗКА
у А уВ
уС
2
ZА ZВ
ZС
2
АВ
х В х А 2 у В у А 2 ( z B z A ) 2
20.
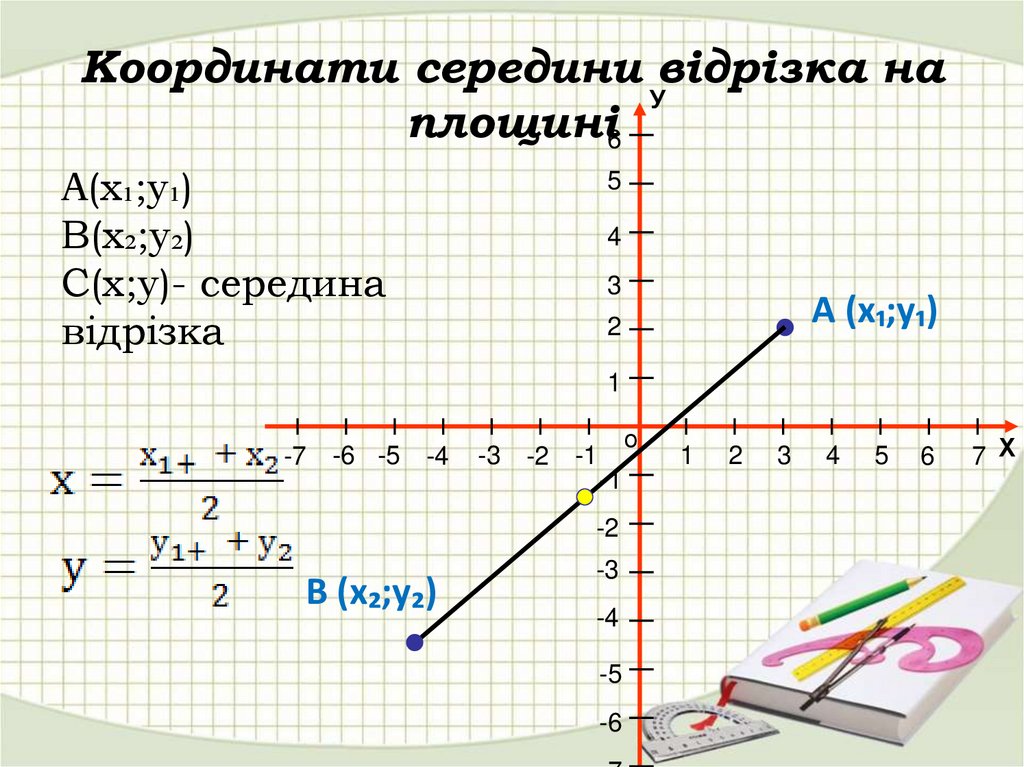
21. Координати середини відрізка на площині
Координати середини відрізка наУ
площині6
А(х₁;у₁)
В(х₂;у₂)
С(х;у)- середина
відрізка
5
4
3
А (х₁;у₁)
2
1
-7
-6 -5
-4
-3
-2
о
-1
-1
-2
В (х₂;у₂)
-3
-4
-5
-6
1
2
3
4
5
6
7 Х
22.
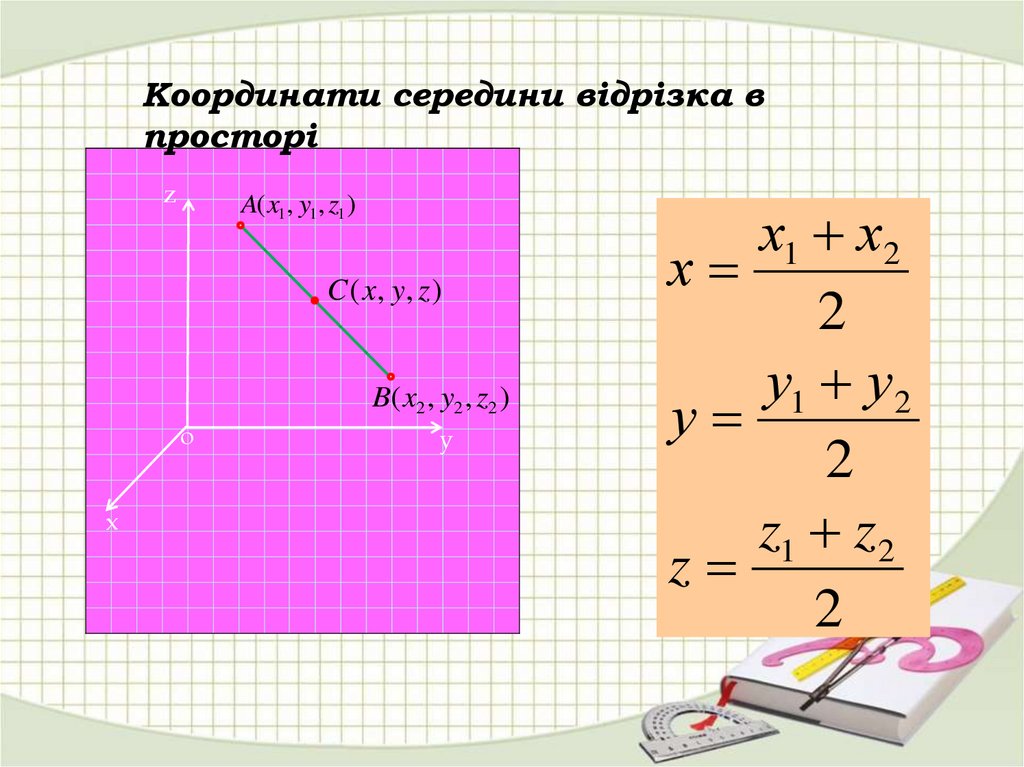
Координати середини відрізка впросторі
z
A( x1, y1, z1 )
C ( x, y , z )
B( x2 , y2 , z2 )
o
x
y
х1 х2
х
2
у1 у2
у
2
z1 z 2
z
2





















 Математика
Математика








