Похожие презентации:
Функції багатьох змінних
1. ФУНКЦІЇ БАГАТЬОХ ЗМІННИХ
Функція двох зміннихЧастинна похідна.
Диференціал функції.
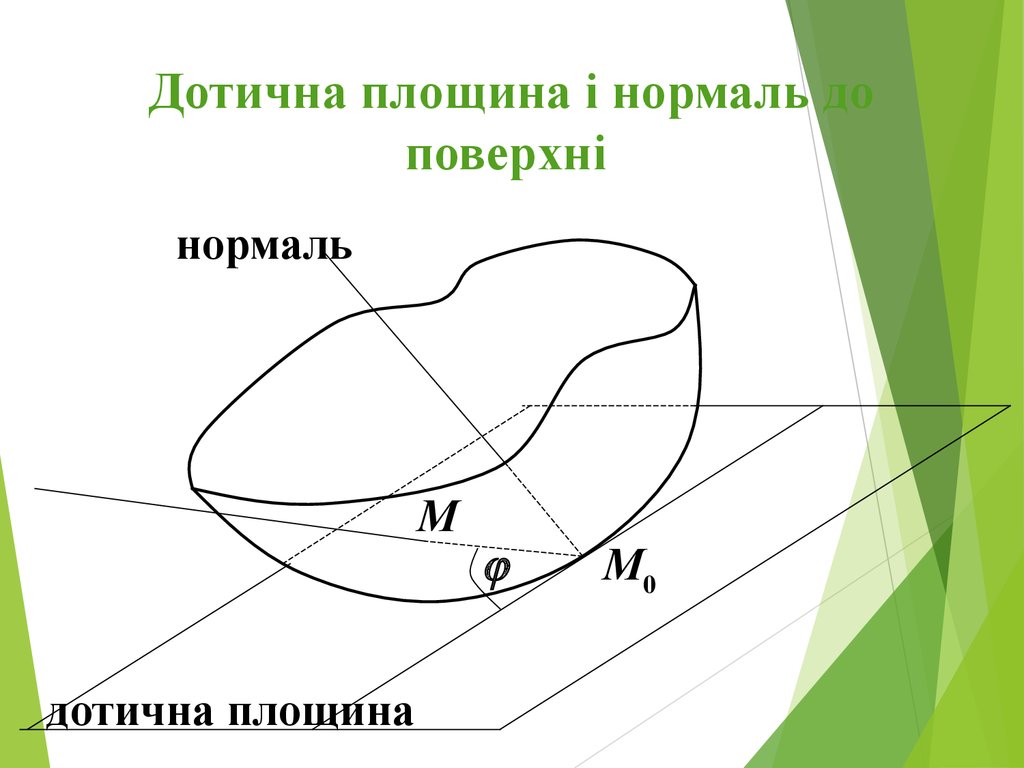
Дотична площина і нормаль до поверхні
Градієнт
Застосування диференціала для наближених обрахунків.
Дослідження функції двох змінних на умовний екстремум
Найбільше і найменше значення функції в замкненій області
2. Функція двох змінних
z f ( x, y )z f (M )
3. Функція двох змінних
4. Функція двох змінних
5. Функція двох змінних
6. Частинні прирости і частинні похідні
7. Частинні прирости і частинні похідні
xzlim
x 0 x
lim
y 0
yz
y
¶z
¶f ( x, y )
; z¢x ;
;
¶x
¶x
f x¢( x, y ).
¶z
; z¢y ;
¶y
f y¢( x, y ).
¶f ( x, y )
;
¶y
8. Частинні прирости і частинні похідні
9. Частинні прирости і частинні похідні
10. Повний приріст і повний диференціал
11. Повний приріст і повний диференціал
12. Повний приріст і повний диференціал
z f ( x x, y y ) f ( x, y )dz f x¢( x, y )dx f y¢( x, y )dy
¶z
¶z
dz dx dy
¶x
¶y
2
2
2
¶
z
¶
z
¶
z 2
2
2
d z 2 dx 2
dxdy 2 dy
¶x¶y
¶x
¶y
¶u
¶u
¶u
du
dx dy dz
¶x
¶y
¶z
13. Дотична площина і нормаль до поверхні
нормальМ
дотична площина
М0
14.
F ( x, y , z ) 0( Fx¢ ) M
0
( x x0 ) ( Fy¢ )
M 0 ( x0 , y 0 , z 0 )
M0
( y y0 ) ( Fz¢) M ( z z0 ) 0
0
x x0
y y0
z z0
( Fx¢ ) M 0 ( Fy¢ )
( Fz¢) M 0
M0
z f ( x, y )
z z0 f x¢( x0 , y0 )( x x0 ) f y¢( x0 , y0 )( y y0 )
x x0
y y0
z z0
f x¢( x0 y0 ) f y¢( x0 , y0 )
1
15.
22
z x 2 xy y x 2 y
М(1, 1, 1)
¶z
¶z
2 x 2 y 1;
2 x 2 y 2
¶x
¶y
¶z
¶z
1;
2;
¶x M
¶y M
z 1 ( x 1) 2( y 1) или
x 2y z 0
x 1 y 1 z 1
1
2
1












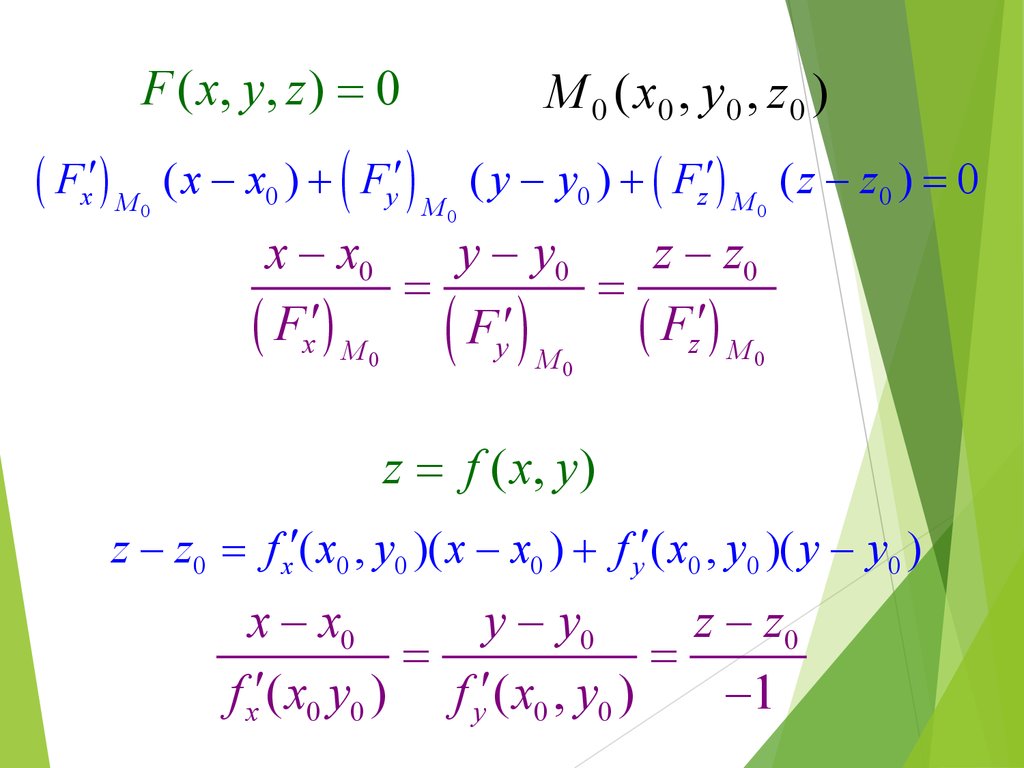

 Математика
Математика








