Центр тяжести плоских фигур

1.

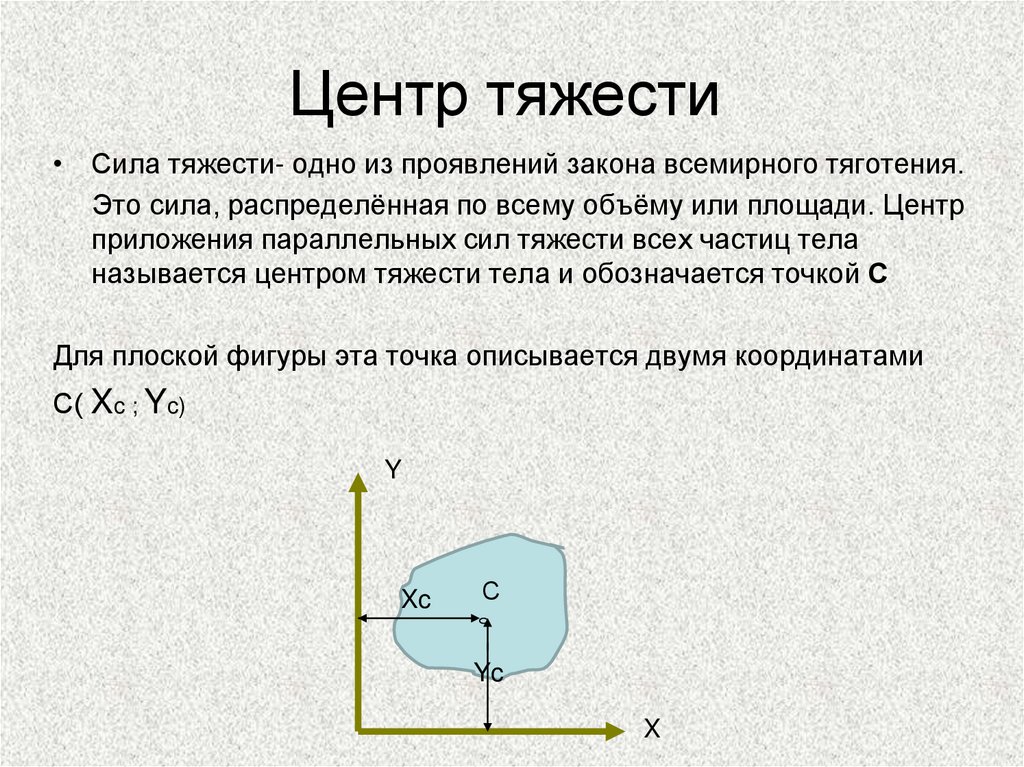
Центр тяжести
• Сила тяжести- одно из проявлений закона всемирного тяготения.
Это сила, распределённая по всему объёму или площади. Центр
приложения параллельных сил тяжести всех частиц тела
называется центром тяжести тела и обозначается точкой С
Для плоской фигуры эта точка описывается двумя координатами
С( Xc ; Yc)
Y
Xc
С
Yc
X

2.

Положение центра тяжести простых
фигур
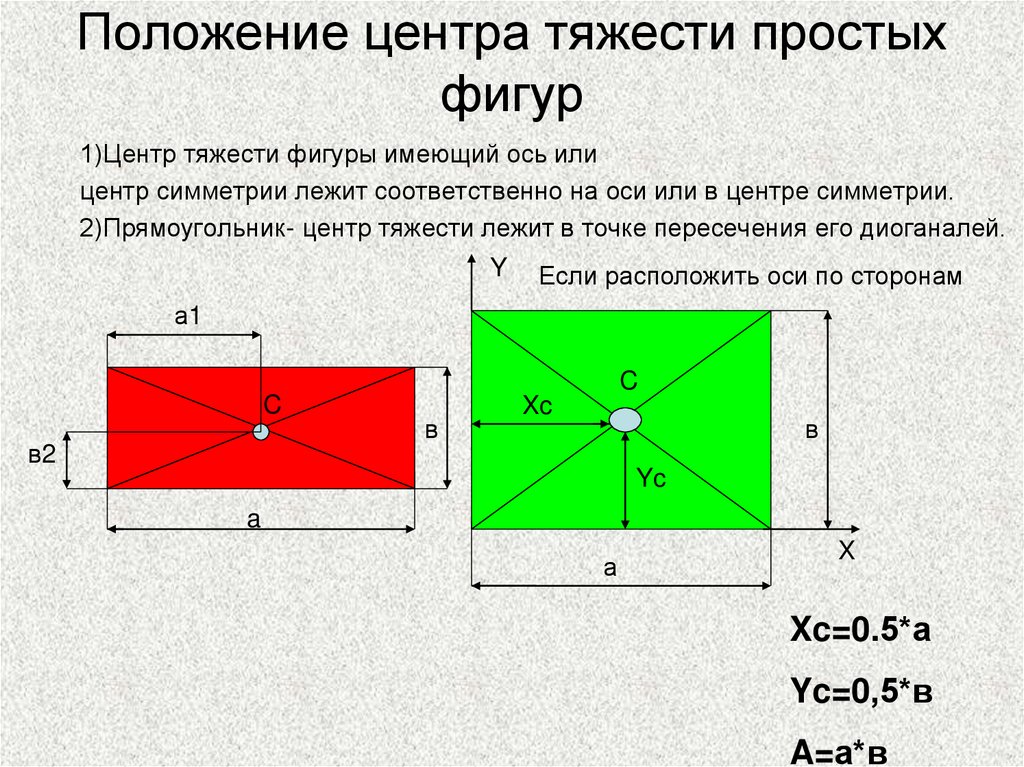
1)Центр тяжести фигуры имеющий ось или
центр симметрии лежит соответственно на оси или в центре симметрии.
2)Прямоугольник- центр тяжести лежит в точке пересечения его диоганалей.
Y
Если расположить оси по сторонам
а1
C
C
в2
в
Xc
в
Yc
a
а
X
Xc=0.5*а
Yc=0,5*в
A=а*в

3.

Положение центра тяжести простых
фигур
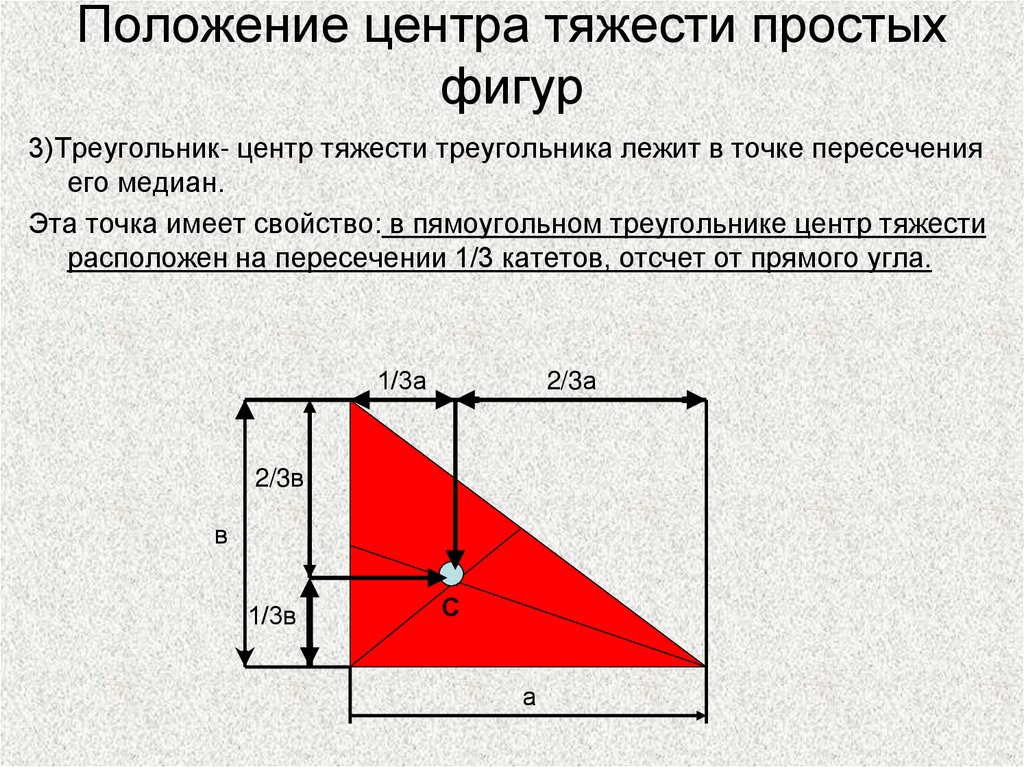
3)Треугольник- центр тяжести треугольника лежит в точке пересечения
его медиан.
Эта точка имеет свойство: в пямоугольном треугольнике центр тяжести
расположен на пересечении 1/3 катетов, отсчет от прямого угла.
1/3а
2/3а
2/3в
в
1/3в
С
а

4.

Если расположить оси по катетам
Y
Xc=1/3a
Yc=1/3a
A=0.5aв
в
C
Yc
X
Xc
а

5.

Полукруг
Y
r
0
0
C
X
Xc=0.424*r
0.424r
Xc
Yc=0
A=∏r2 / 2

6.

Формулы для определения
сложных сечений
Xc=Sy / Аоб = (∑Ai Xci) / ∑Ai
Yc=Sx / Aоб=( ∑AiYci) / ∑Ai

7.

Методика решения
1.
2.
3.
4.
5.
6.
7.
8.
9.
Изобразить сечение в натуральную величину или в масштабе.
Разбить сложные сечения на простые составляющие.
Определить положение центра тяжести каждого сечения
построением.
Выбрать систему координат.
Показать размерными линиями абсциссы и ординаты.
Рассчитать координаты центров тяжести всех сечений , а также их
площади.
По формулам рассчитать координаты центра тяжести сложного
сечения.
Изобразить полученную точку на сечении.
Рекомендуется изобразить точку (С) на отдельно сделанном в
том же масштабе модели с помощью подвешивания в двух точках
и проверить соответствие расчетной и экспериментальной точке
друг к другу.

8.

Пример решения
• Рисунок.
Y
Xc2
c2
C
Xc
Xc1
90
c1 Yc2
60
Yc
R20
Yc1
c3
Xc3
90
Yc3
X

9.

Пример решения
Решение
Xc1=0.5*9=4.5 (см)
Yc1=0.5*6=3 (см)
A1=9*6=54 (cм2)
Xc2=⅔*6-9=6(cм)
Yc2=6+⅓*(9-6)=7(см)
A2=0,5*9*(9-6)=13,5(см 2)
Xc3=9-0,424*R=9-0.9=8.1(cм)
Yc3=R=2(cм)
A3= - ПR2/2= - 6.28 (см 2)
Xc = Sy / A= (Xc1A1+Xc2A2+Xc3A3 ) / (A1+A2+A3) = 4.47(см)
Yc = Sx / A= (Yc1A1=Yc2A2=Yc3A3) / (A1=A2=A3) = 4 (см)