Геометрические характеристики плоских сечений. Центр тяжести плоской фигуры

1.

Лекция № 3
Геометрические характеристики плоских сечений Центр
тяжести плоской фигуры. Статический момент сечения и
моменты инерции сечений. Радиус инерции. Расчет моментов
инерции простейших фигур.

2.

Геометрические характеристики плоских сечений:
Sx ydA - статический момент сечения относительно оси х;
A
Sy xdA - статический момент сечения относительно оси у;
A
J x y 2 d Α - осевой момент инерции сечения относительно оси х;
A
J y x 2 d Α - осевой момент инерции сечения относительно оси у;
A
J xy xydA
- центробежный момент инерции сечения относительно
A
осей х, у;
J 2 d Α - полярным моментом инерции сечения относительно
центра О,
A
где А – площадь сечения.
Ось, относительно которой статический момент равен нулю, называется
центральной.
Точка пересечения центральных осей называется центром тяжести
сечения.

3.

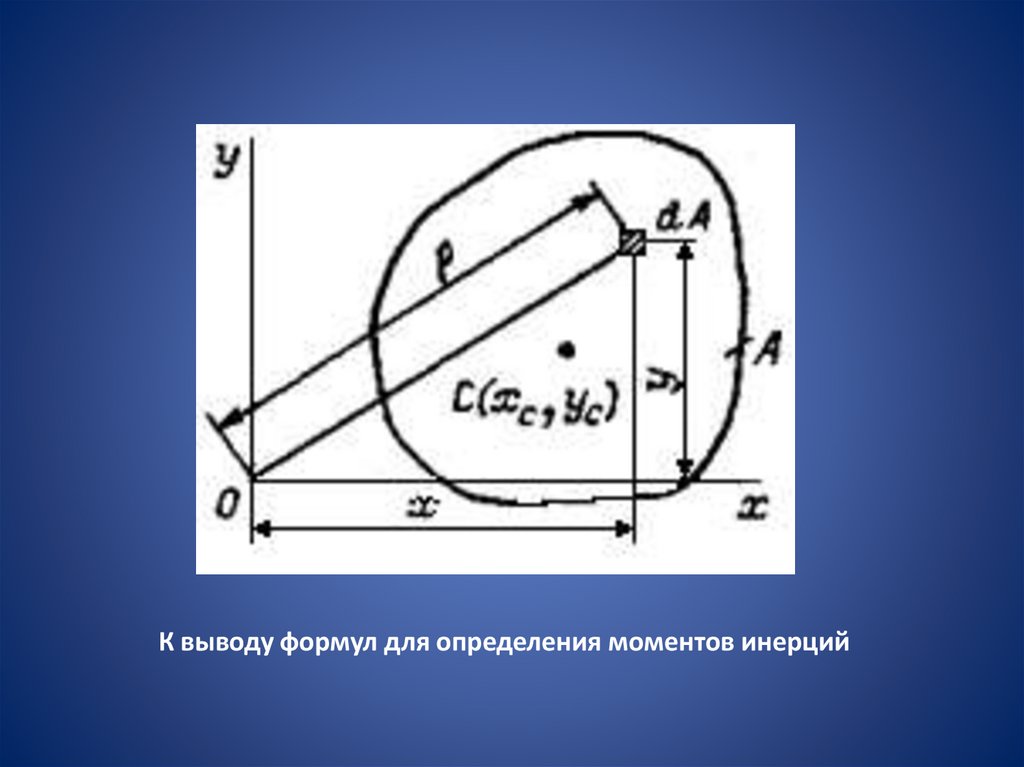
К выводу формул для определения моментов инерций

4.

Расчетные величины :
ix ─ радиус инерции сечения относительно оси х
ix
Jx
A
,
iy ─ радиус инерции сечения относительно оси у
iy
Jy
A
.

5.

Если положение центра тяжести какой-либо фигуры известно, то
статический момент этой фигуры относительно оси
,
Sx Ay
C
где ус — ордината центра тяжести фигуры.
Если известен статический момент Sx относительно какой либо оси, можно
найти ус : y Sx A .
C

6.

Если фигуру можно представить в виде отдельных простых фигур
(прямоугольников, треугольников и т. п.), для которых известны положения
центров тяжести, статический момент всей фигуры можно получить
суммированием статических моментов этих простых фигур. Это следует из
свойств определенного интеграла.
Для стандартных профилей (двутавр, швеллер и др.) значения Sx и Sy
приведены в справочниках.
Если фигура имеет ось симметрии, то последняя всегда проходит через
центр тяжести фигуры, а поэтому статический момент фигуры
относительно оси симметрии всегда равен нулю.

7.

При параллельном переносе осей (х1 = х - а; y1 = y - b) моменты инерции
определяются следующими выражениями:
J x1 J x b 2 A
,
J y1 J y a 2 A
,
J x1 y1 J xy abA
.
Осевые и полярный моменты инерции являются величинами всегда
положительными ( J x 0 , J y 0
, J 0 ),
центробежный момент инерции - величина знакопеременная ( J xy 0 ).
Моменты инерции стандартных профилей (двутавр, швеллер, уголок)
приведены в справочниках.

8.

К выводу формул для определения моментов инерций
при параллельном переносе осей

9.

Если при повороте осей один из осевых моментов инерции достигает
своего максимального значения, то другой момент инерции принимает
минимальное значение.
Если одна из осей х или у, либо обе оси одновременно являются осями
симметрии, то относительно этих осей центробежный момент инерции
равен нулю.
Оси, относительно которых центробежный момент инерции равен нулю, а
осевые моменты инерции принимают экстремальные значения,
называются главными осями инерции.
Главные оси, проходящие через центр тяжести сечения, называются
главными центральными осями.
Осевые моменты инерции относительно главных осей называются
главными моментами инерции.

10.

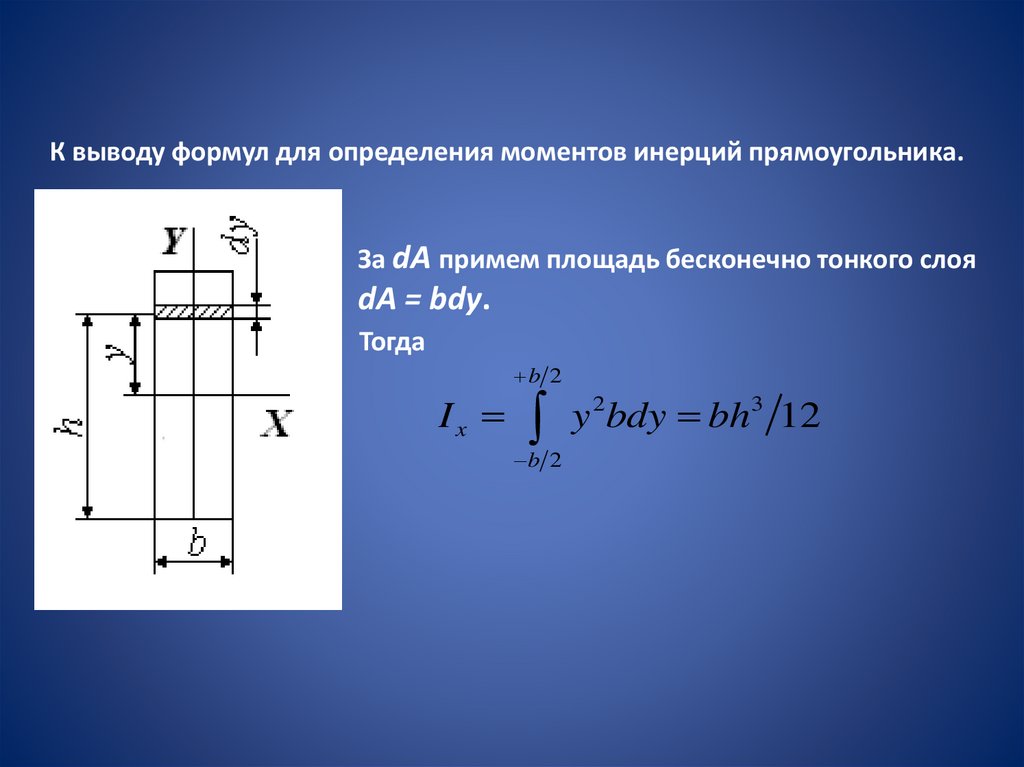
К выводу формул для определения моментов инерций прямоугольника.
За dA примем площадь бесконечно тонкого слоя
dA = bdy.
Тогда
b 2
Ix
b 2
y 2bdy bh3 12

11.

К выводу формул для определения моментов инерций круга.
За dA примем площадь бесконечно
тонкого кольца толщиной dρ .
Тогда dA = 2πρdρ.
r
I 2 2 d r 4 2 0,1d 4
0
Так как
IX = IY ,
I X IY I 2 r 4 4 d 4 32 0, 05d 4
.

12.

Сумма моментов инерции относительно любых взаимно
перпендикулярных осей не меняется при их повороте.
Существует такой угол α, при котором один из моментов инерции
достигает своего максимального значения, в то время как другой момент
инерции становится минимальным.
tg 2 2 I XY ( IY I X )
При этом значении угла α один из осевых моментов инерции будет
наибольшим, а другой — наименьшим. Одновременно центробежный
момент инерции IXY при данном угле α равен 0.

13.

Значения главных моментов инерции
I max I X IY
I min I X IY
IY I X
2
2
4 I XY
2
I
I
4
I
Y X
XY
2
2
2
,

14.

Из формул следует, что если два главных центральных момента инерции
равны между собой, то у этого сечения любая центральная ось является
главной и все главные центральные моменты инерции одинаковы (круг,
кольцо, квадрат, шестиугольник, равносторонний треугольник).