Угол между прямой и плоскостью (Задание 13)

1.

Задание 13.
Угол между прямой
и плоскостью

2.

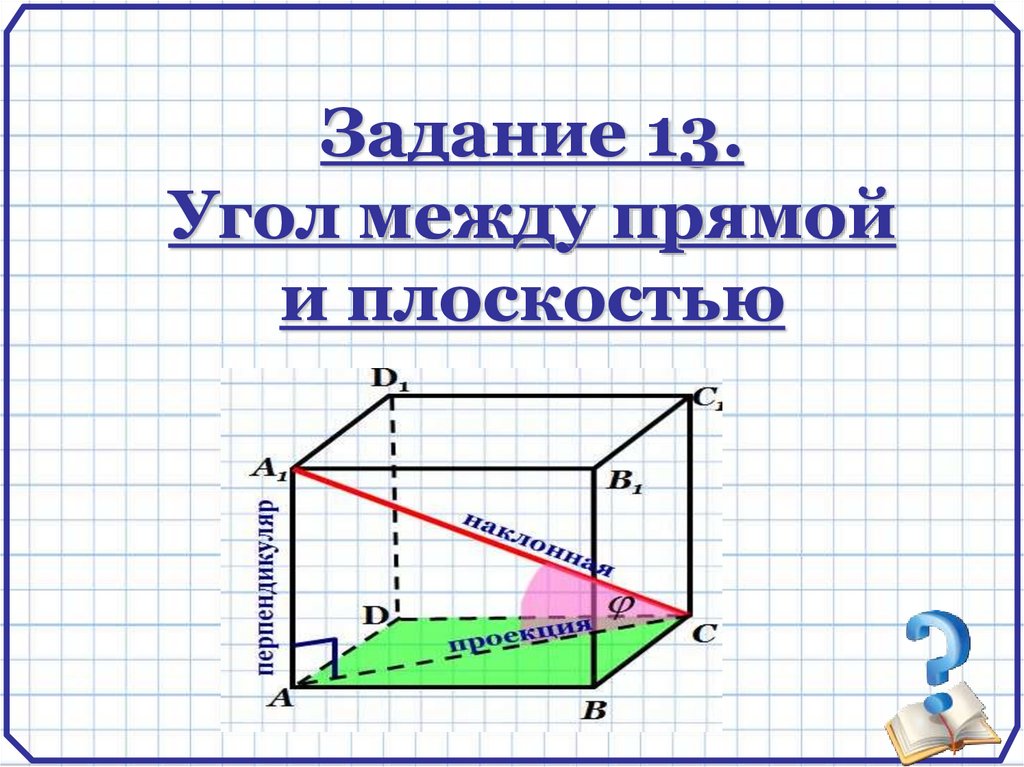
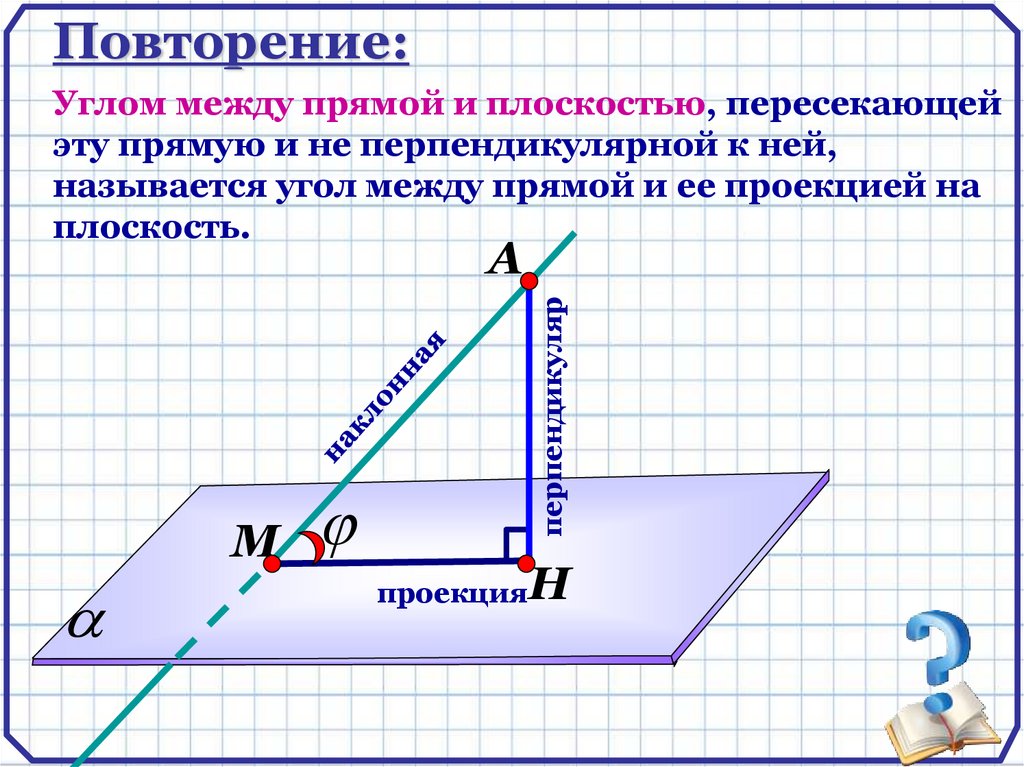
Повторение:
Углом между прямой и плоскостью, пересекающей
эту прямую и не перпендикулярной к ней,
называется угол между прямой и ее проекцией на
плоскость.
М
перпендикуляр
А
проекция Н

3.

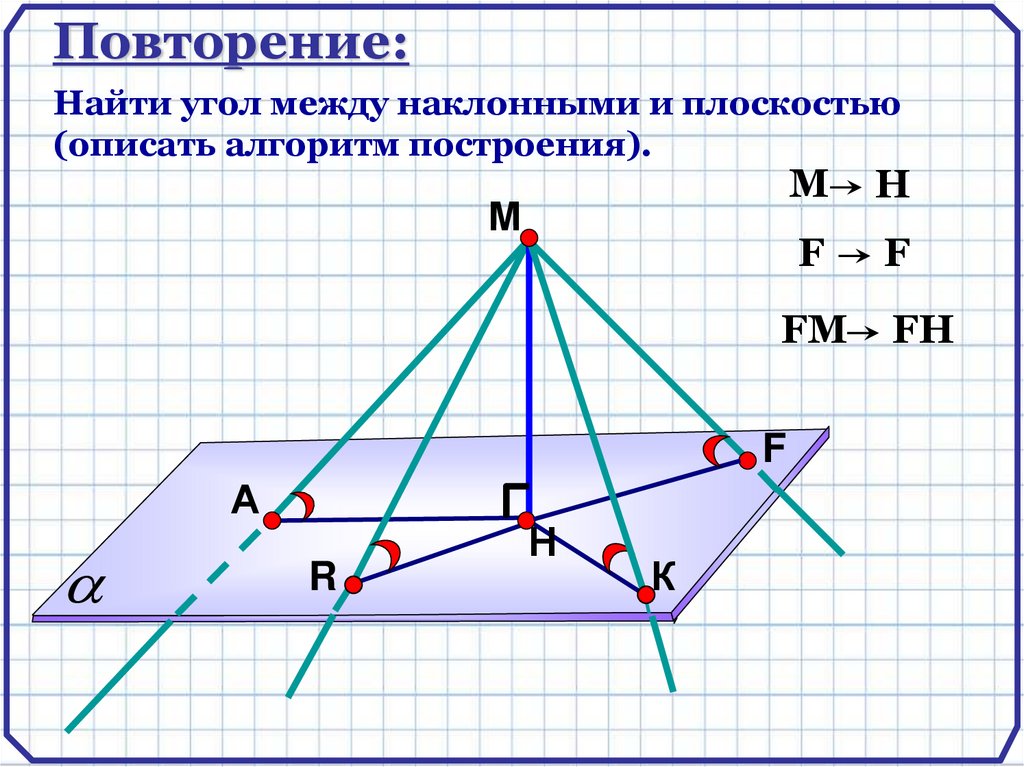
Повторение:
Найти угол между наклонными и плоскостью
(описать алгоритм построения).
М
М
H
F
F
FМ
F
А
R
Н
К
FH

4.

Повторение:
Угол между прямой m и плоскостью можно
вычислить:
1) Если этот угол удается включить в прямоугольный
треугольник в качестве одного из острых углов;
2) Используя векторный метод;
3) Используя координатно –векторный метод;
4) Используя ключевые задачи;

5.

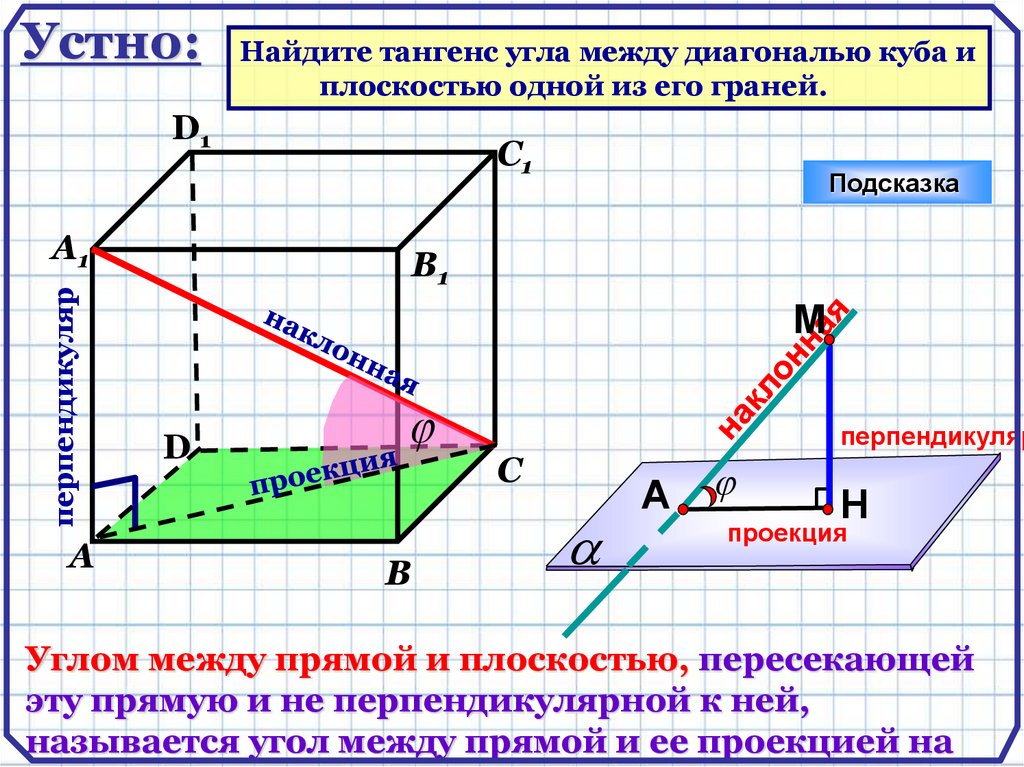
Устно:
Найдите тангенс угла между диагональю куба и
плоскостью одной из его граней.
D1
перпендикуляр
А1
А
С1
Подсказка
В1
М
D
В
перпендикуляр
С
А
Н
проекция
Углом между прямой и плоскостью, пересекающей
эту прямую и не перпендикулярной к ней,
называется угол между прямой и ее проекцией на

6.

№1
В единичном кубе АВСДА1В1С1Д1 найдите
тангенс угла между прямой АА1 и
плоскостью ВС1Д .
D1
С1 1) Прямая AА1 параллельна
1
А1
В1
1
2
2
D
О
А
1
В
прямой СС1, Угол между
прямой АА1 и плоскостью ВС1Д .
равен углу между СС1 и
плоскостью ВС1Д.
ВД ДВС1
1
ВД АС ДВС1 ОС1С
ВД СС1
С 2. Прямая СС проецируется на
1
плоскость ВС1Д в прямую ОС1.
Поэтому проекция точки С
лежит на отрезке ОС1. Значит,
прямая ОС1 является проекцией
прямой СС1, следовательно, угол
ОС1С искомый.
Ответ: 2
2

7.

Критерии оценивания выполнения задания С2
баллы
Критерии оценивания
2
Правильный ход решения. Верно построен или
описан искомый угол. Получен верный ответ
1
1) Правильный ход решения. Получен верный
ответ, но имеется ошибка в построении и описании
искомого угла, не повлиявшая на ход решения
2) Правильный ход решения. Верно построен и
описан искомый угол, но имеется ошибка в одном
из
вычислений,
допущенная
из-за
невнимательности, в результате чего получен
неверный ответ
0
1) Ход решения правильный, но оно не доведено до
конца, или решение отсутствует. Нет ответа
2) Ход решения правильный, но имеются
существенные ошибки в вычислениях, приведшие
к неправильному ответу
3) Неправильный ход решения, приведший к
неверному ответу
4) Верный ответ получен случайно при неверном

8.

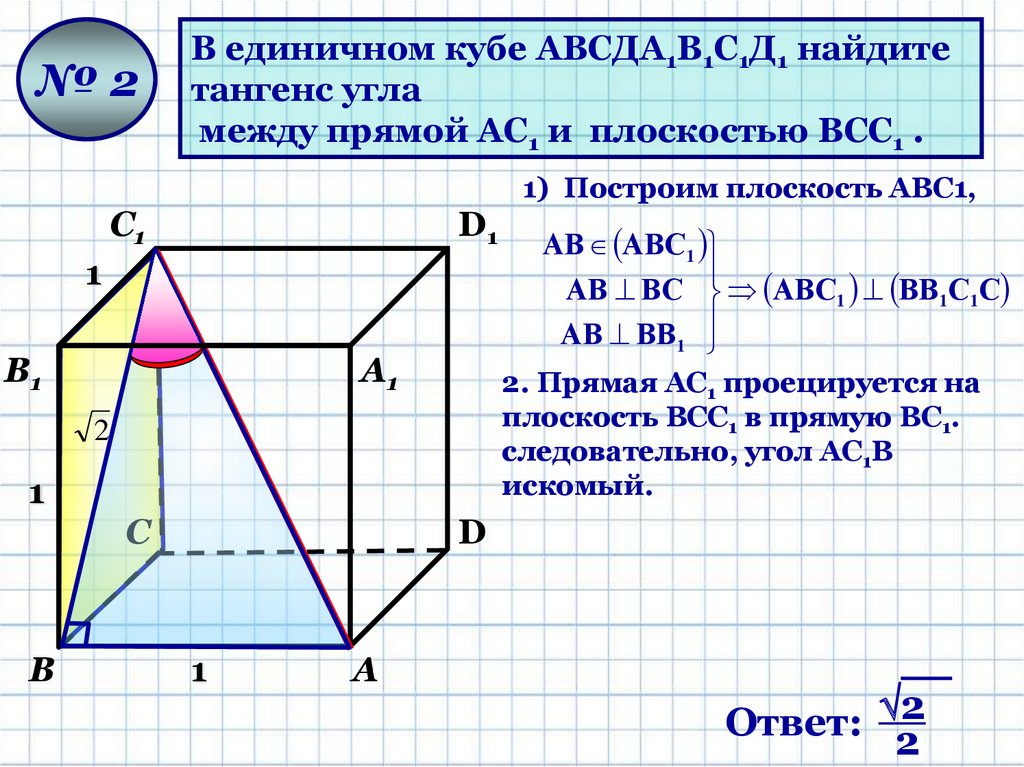
№2
В единичном кубе АВСДА1В1С1Д1 найдите
тангенс угла
между прямой АС1 и плоскостью ВСС1 .
1) Построим плоскость AВС1,
С1
D1
1
В1
А1
2. Прямая АС1 проецируется на
плоскость ВСС1 в прямую ВС1.
следовательно, угол АС1В
искомый.
2
1
С
В
АВ АВС1
АВ ВС АВС1 ВВ1С1С
АВ ВВ1
D
1
А
Ответ: 2
2

9.

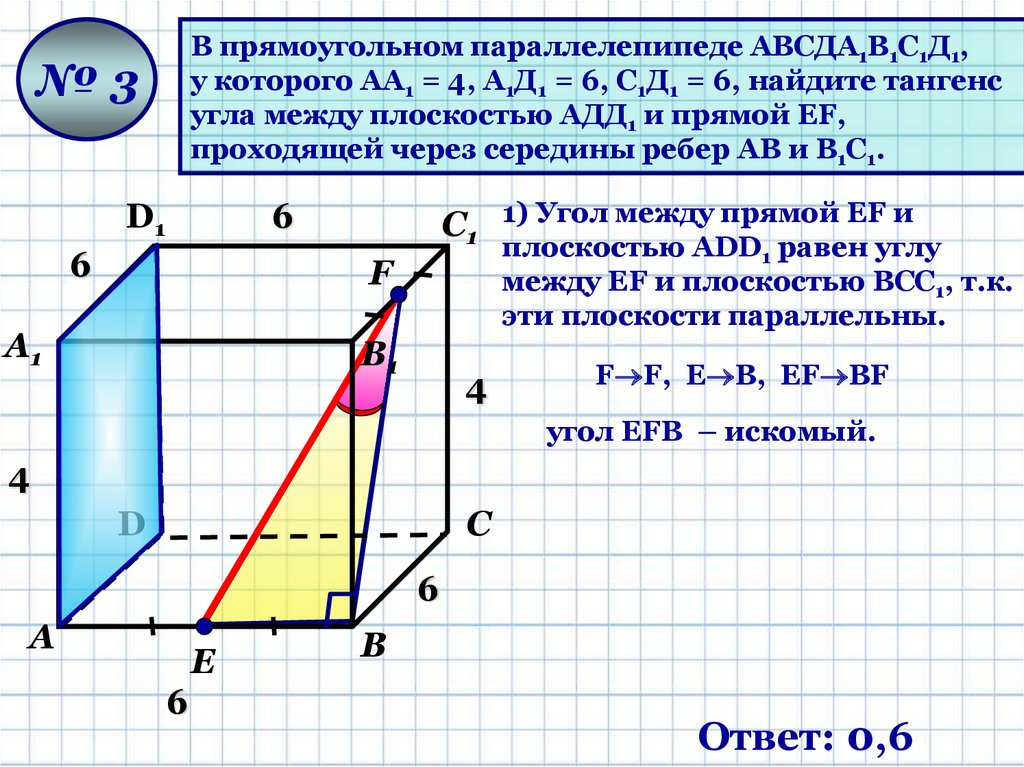
В прямоугольном параллелепипеде АВСДА1В1С1Д1,
у которого АА1 = 4, А1Д1 = 6, С1Д1 = 6, найдите тангенс
угла между плоскостью АДД1 и прямой ЕF,
проходящей через середины ребер АВ и В1С1.
№3
D1
С1 1) Угол между прямой EF и
6
6
плоскостью АDD1 равен углу
между EF и плоскостью ВСС1, т.к.
эти плоскости параллельны.
F
А1
В1
4
F F, Е В, ЕF ВF
угол EFB – искомый.
4
D
С
6
А
Е
6
В
Ответ: 0,6

10.

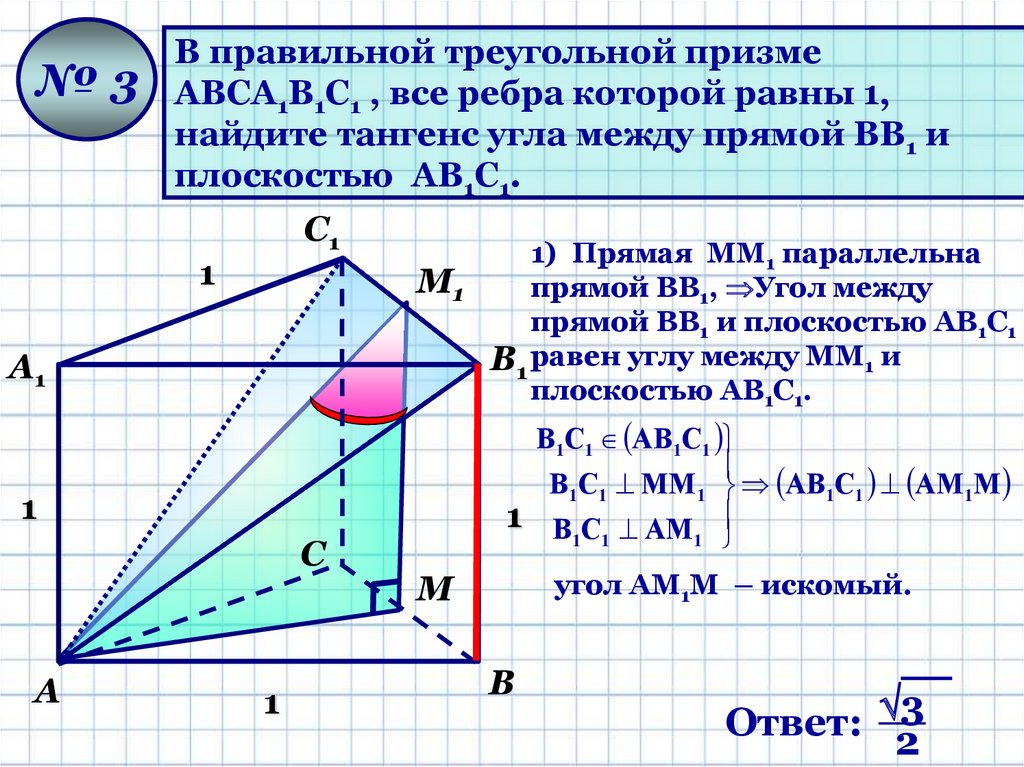
№3
В правильной треугольной призме
АВСА1В1С1 , все ребра которой равны 1,
найдите тангенс угла между прямой ВВ1 и
плоскостью АВ1С1.
С1
1
М1
А1
В1С1 АВ1С1
В1С1 ММ 1 АВ1С1 АМ 1М
1 В С АМ
1 1
1
1
С
А
1
1) Прямая ММ1 параллельна
прямой ВВ1, Угол между
прямой ВВ1 и плоскостью АВ1С1
В1 равен углу между ММ1 и
плоскостью АВ1С1.
угол АМ1М – искомый.
М
В
Ответ: 3
2

11.

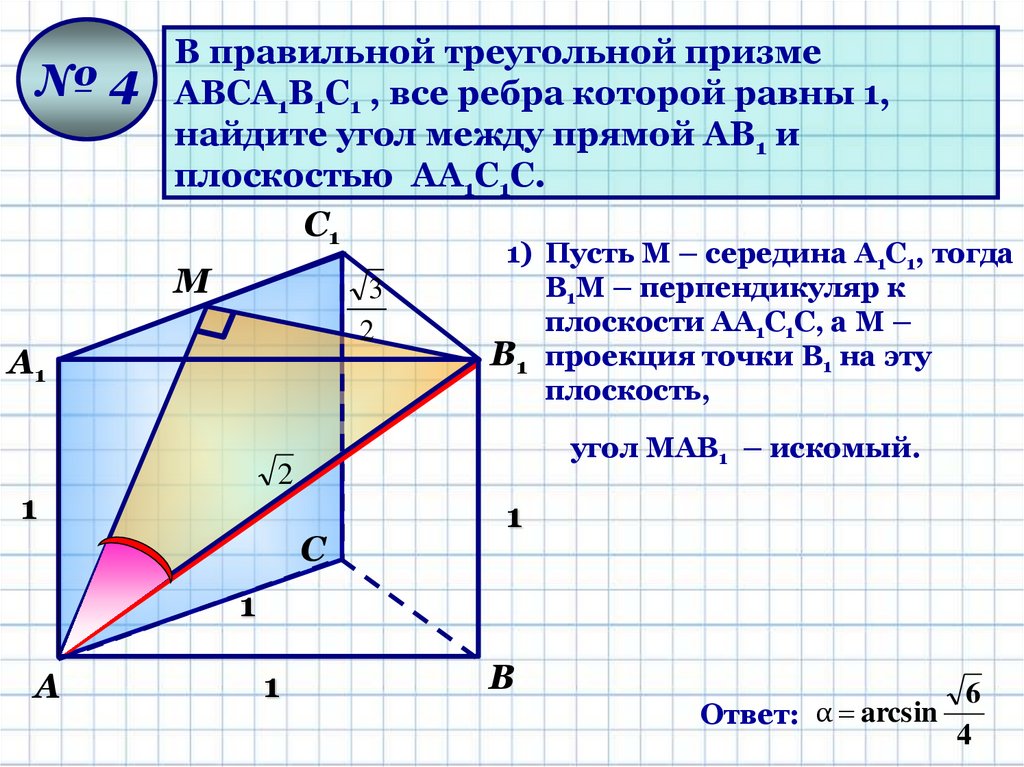
№4
В правильной треугольной призме
АВСА1В1С1 , все ребра которой равны 1,
найдите угол между прямой АВ1 и
плоскостью АА1С1С.
С1
М
3
2
А1
1) Пусть М – середина А1С1, тогда
В1М – перпендикуляр к
плоскости АА1С1С, а М –
В1 проекция точки В1 на эту
плоскость,
угол МАВ1 – искомый.
2
1
С
1
1
А
1
В
Ответ: α arcsin
6
4

12.

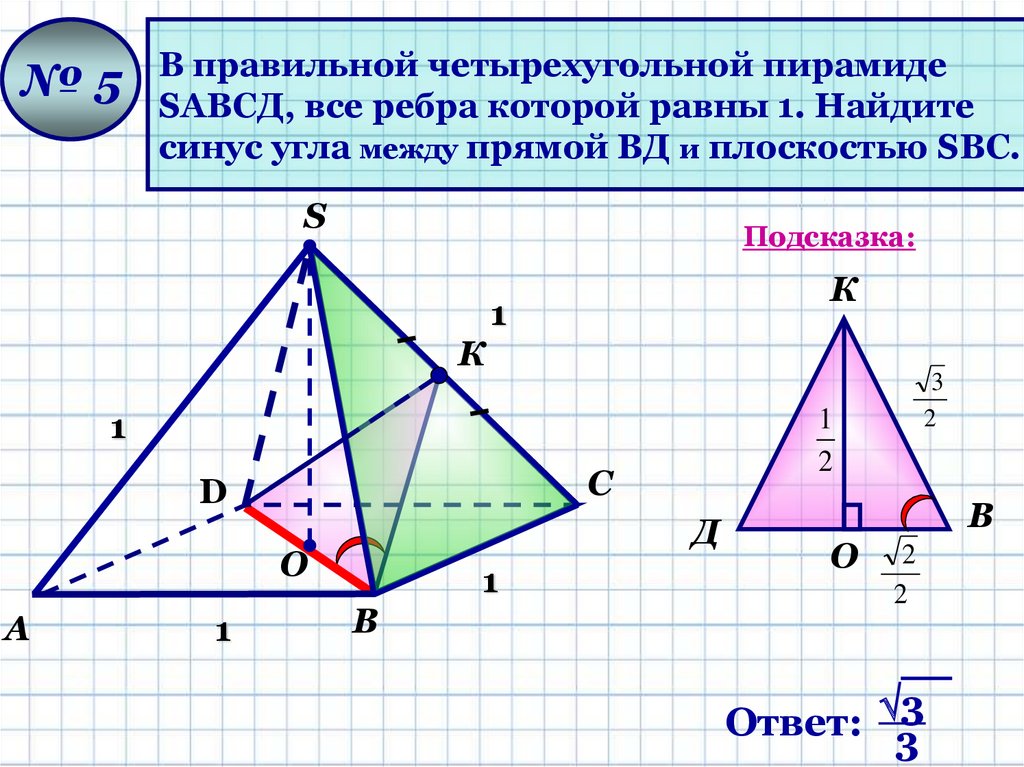
№5
В правильной четырехугольной пирамиде
SАВСД, все ребра которой равны 1. Найдите
синус угла между прямой ВД и плоскостью SВС.
S
Подсказка:
К
1
К
1
Д
О
А
1
1
2
С
D
1
В
3
2
В
О
2
2
Ответ: 3
3

13.

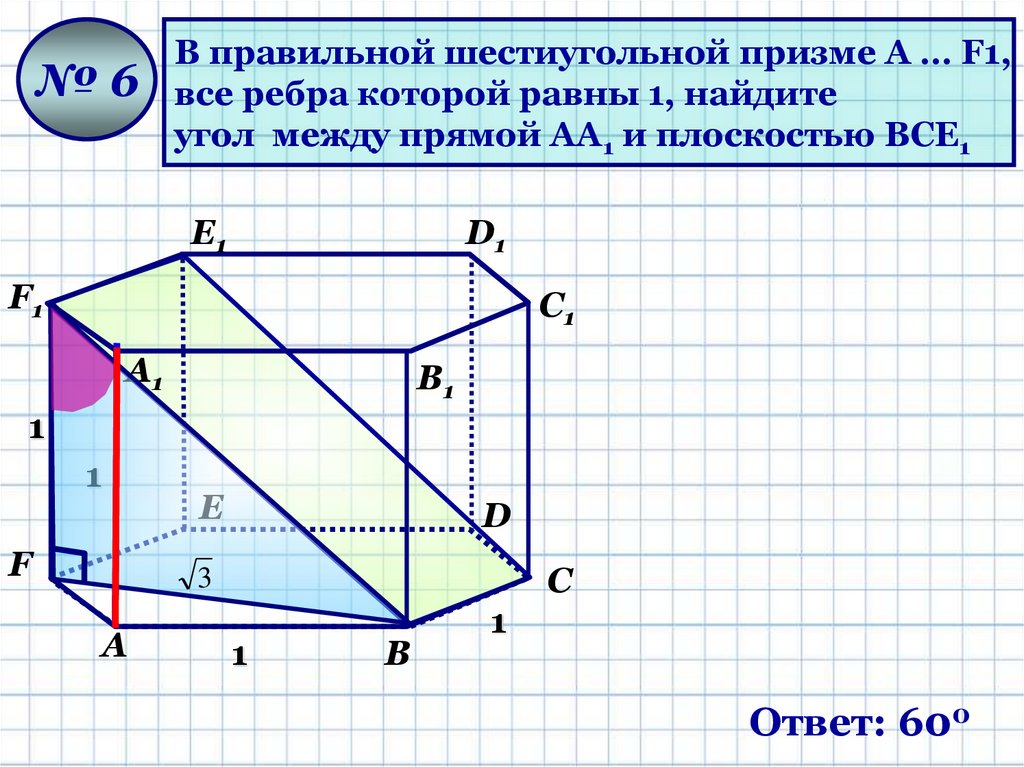
№6
В правильной шестиугольной призме A … F1,
все ребра которой равны 1, найдите
угол между прямой AА1 и плоскостью BCЕ1
Е1
D1
F1
С1
А1
В1
1
1
F
Е
D
С
3
А
1
В
1
Ответ: 600

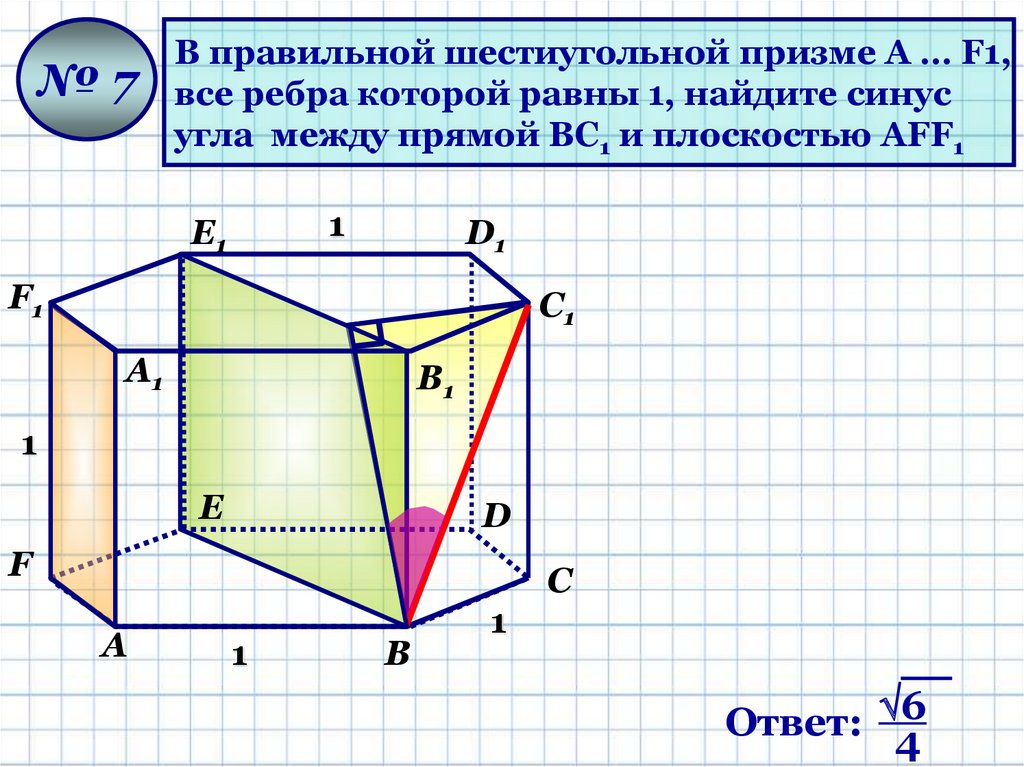
14.

№7
В правильной шестиугольной призме A … F1,
все ребра которой равны 1, найдите синус
угла между прямой BС1 и плоскостью АFF1
1
Е1
D1
F1
С1
А1
В1
1
Е
D
F
С
А
1
В
1
Ответ: 6
4

15.

Домашнее задание
В единичном кубе АВСДА1В1С1Д1 точка Е – середина
ребра А1В1. Найдите синус угла между прямой АЕ и
плоскостью ВДД1.
10
10
Ответы :
В прямоугольном параллелепипеде АВСДА1В1С1Д1,
у которого АВ = 4, ВС = 6, СС1 = 4, найдите тангенс
угла между плоскостью АВС и прямой ЕF,
проходящей через середины ребер АА1 и С1Д1.
Ответы :
1
10
В правильной шестиугольной призме
АВСДЕFА1В1С1Д1Е1F1, все ребра которой равны 1,
найдите угол между прямой СС1 и плоскостью BДЕ1 .
Ответы : 450

16.

Литература
1. В.А. Смирнов ЕГЭ 2011. Математика.
Задача С2. Геометрия. Стереометрия. /
Под. редакцией А.Л. Семенова и И.В.
Ященко. – М.: МЦНМО, 2011.