Похожие презентации:
Определители и методы их вычисления. Лекция 2
1.
СЛАЙД-ЛЕКЦИЯ № 2ТЕМА ЛЕКЦИИ:
«ОПРЕДЕЛИТЕЛИ
И МЕТОДЫ ИХ ВЫЧИСЛЕНИЯ»
1
2. ПЛАН ЛЕКЦИИ
1. ОПРЕДЕЛИТЕЛЬ КВАДРАТНОЙМАТРИЦЫ
2. МИНОРЫ И АЛГЕБРАИЧЕСКИЕ
ДОПОЛНЕНИЯ
3. СПОСОБЫ ВЫЧИСЛЕНИЯ
ОПРЕДЕЛИТЕЛЕЙ
2
3. ОПРЕДЕЛИТЕЛЬ КВАДРАТНОЙ МАТРИЦЫ
34.
• Определителем (детерминантом)матрицы n-го порядка называется число:
n det A
a11
a12
... a1n
a 21
a 22
... a 2 n
...
...
...
a n1
an2
... a nn
...
5. ОБОЗНАЧЕНИЯ
КВАДРАТНАЯ МАТРИЦА n-го ПОРЯДКАa11
A
a
n1
a1n
ann
ОБОЗНАЧЕНИЯ ОПРЕДЕЛИТЕЛЯ МАТРИЦЫ
a11
a1n
an1
ann
A det A
5
6. ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЕЙ МАТРИЦ 1-го и 2-го ПОРЯДКОВ
ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 1-го ПОРЯДКАa11 a11
ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 2-го ПОРЯДКА
a11
a12
a21 a22
a11 a22 a21 a12
6
7.
2a11
a12
a21 a22
2
a11a22 a12a21
8.
Примеры:1)
2)
3)
3 2
1
5
3 5 2 1 15 ( 2) 17
cos x sin x
sin x
cos x
cos 2 x sin 2 x cos 2 x
cos x sin x
sin x
cos x
cos x sin x 1
2
2
9.
10. МИНОРЫ И АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ
1011. МИНОР ЭЛЕМЕНТА ОПРЕДЕЛИТЕЛЯ
МИНОРОМ ЭЛЕМЕНТА ОПРЕДЕЛИТЕЛЯНАЗЫВАЕТСЯ ОПРЕДЕЛИТЕЛЬ,
ПОЛУЧЕННЫЙ ИЗ ИСХОДНОГО
ОПРЕДЕЛИТЕЛЯ ПРИ ПОМОЩИ
ВЫЧЕРКИВАНИЯ СТРОКИ И
СТОЛБЦА, В КОТОРЫХ
СТОИТ ЭТОТ ЭЛЕМЕНТ
11
12. ПРИМЕР ВЫЧИСЛЕНИЯ МИНОРА
МИНОР M 21 ЭЛЕМЕНТА a21 ОПРЕДЕЛИТЕЛЯ3 1 2
4
2 0
7
9 1
ВЫЧИСЛЯЕТСЯ ТАК:
1 2
M 21
9 1
1 2
9
1
1 18 19
12
13.
14. АЛГЕБРАИЧЕСКОЕ ДОПОЛНЕНИЕ
АЛГЕБРАИЧЕСКИМ ДОПОЛНЕНИЕМ AijЭЛЕМЕНТА aij ОПРЕДЕЛИТЕЛЯ
НАЗЫВАЕТСЯ ЧИСЛО
Aij ( 1)i j M ij ,
ГДЕ M ij МИНОР ЭЛЕМЕНТА aij
14
15.
16. СПОСОБЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛИТЕЛЕЙ
1617. РАЗЛОЖЕНИЕ ПО ЛЮБОЙ СТРОКЕ (ЛЮБОМУ СТОЛБЦУ)
ОПРЕДЕЛИТЕЛЬРАВЕН СУММЕ ПРОИЗВЕДЕНИЙ
ЭЛЕМЕНТОВ ЛЮБОЙ СТРОКИ
(ЛЮБОГО СТОЛБЦА) НА ИХ
АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ
17
18. ПРИМЕР ВЫЧИСЛЕНИЯ ОПРЕДЕЛИТЕЛЯ
РАЗЛОЖИМ ОПРЕДЕЛИТЕЛЬ ПО 2-й СТРОКЕ3 1 2
1 2
4
2 0 ( 1) 2 1
7
9 1
3 2
( 1) 2 2 0
9 1
7 1
( 1) ( 1 18) 1 (3 14) 19 11 8
18
19.
20. МЕТОД ТРЕУГОЛЬНИКОВ ДЛЯ ВЫЧИСЛЕНИЯ ОПРЕДЕЛИ-ТЕЛЕЙ МАТРИЦ 3-го ПОРЯДКА
МЕТОД ТРЕУГОЛЬНИКОВ ДЛЯВЫЧИСЛЕНИЯ ОПРЕДЕЛИТЕЛЕЙ МАТРИЦ 3-го ПОРЯДКА
a12
a33 a31
a22
a
31
a13
a21
a12
a11
a22
a23 a21
a11
a33
a32
a32
a13
a23
20
21.
a11a12
a13
3 a 21
a 22
a 23 a11a 22 a33 a 21a32 a13 a12 a 23 a31
a31
a32
a33
a13 a22 a31 a32 a23 a11 a21a12 a33
22. ПРИМЕР ИСПОЛЬЗОВАНИЯ МЕТОДА ТРЕУГОЛЬНИКОВ
23
5
1 3
3
2
4
1
2 1 1 3 ( 3) ( 3) 5 ( 2) 4
4 1 ( 3) 5 3 1 ( 2) ( 3) 2
2 27 40 12 15 12 26
22
23. ОПРЕДЕЛИТЕЛЬ ТРЕУГОЛЬНОЙ МАТРИЦЫ РАВЕН ПРОИЗВЕДЕНИЮ ЭЛЕМЕНТОВ ГЛАВНОЙ ДИАГОНАЛИ
3 1 20
0
2 0 3 2 1 6
0 1
23
24.
25.
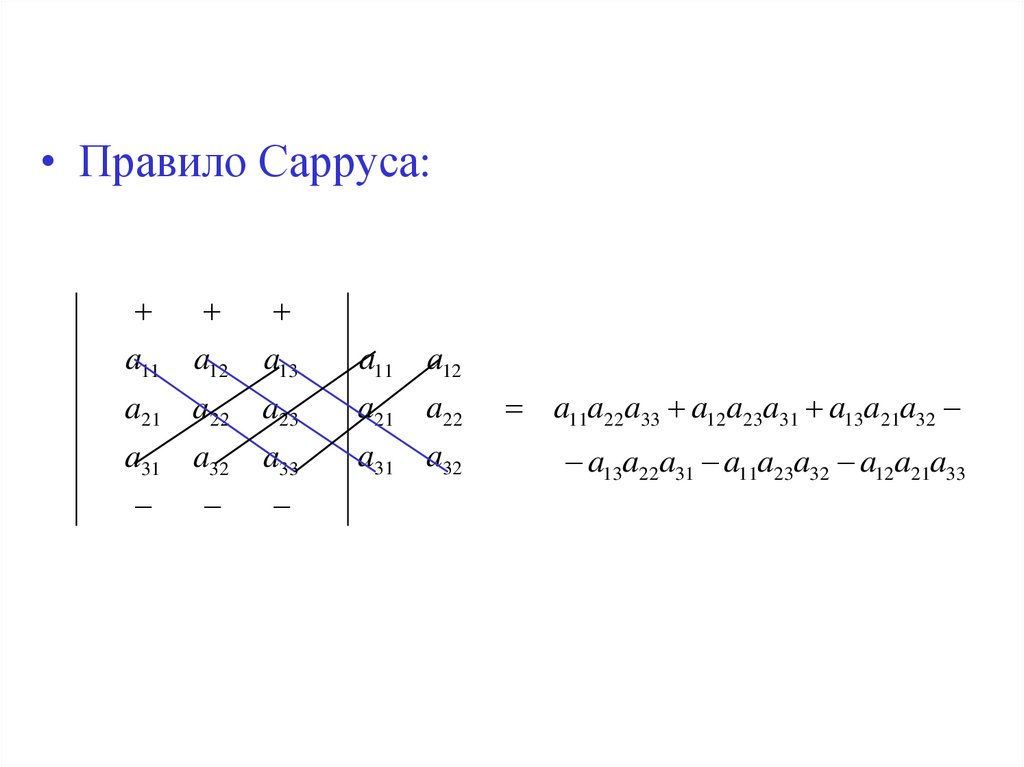
• Правило Сарруса:a11
a12
a13
a11
a21 a22
a23
a21 a22
a31
a32
a33
a31
a12
a32
a11a22a33 a12a23a31 a13a21a32
a13a22a31 a11a23a32 a12a21a33
26.
Примеры:2 4 7
3 1 5 3 1
5 0
7 5 0
4
5)
7
4 ( 1) 7
7 5 5 ( 2) 3 0
5 ( 1) ( 2) 0 5 4 7 3 7
28 175 0 10 0 147 10
27.
28. Свойства определителей.
1.Определитель не изменится, если егоT
транспонировать:
det A det A
det A
3
2 4
det A
T
5
12 10 22
3 2
5
4
12 10 22
29.
2.При перестановке двух строк илистолбцов определитель изменит свой
знак на противоположный.
3
5
2 4
2 4
3
5
12 10 22
10 12 22
30.
3. Общий множитель всех элементовстроки или столбца можно вынести за
знак определителя.
a11
ka12
a21 ka22
k
a11
a12
a21 a22
31.
12
36 12
1
3
2
1
2
2
1
2
1
24 12 3
1
2 12 2 3
1
1
4
1 3 4
1 3 2
24 2 9 2 1 12 3 24 15 360
32.
4. Определитель с двумя одинаковымистроками или столбцами равен нулю.
1
1
3
1
1
3
2 1 4
4 3 6 6 3 4 0






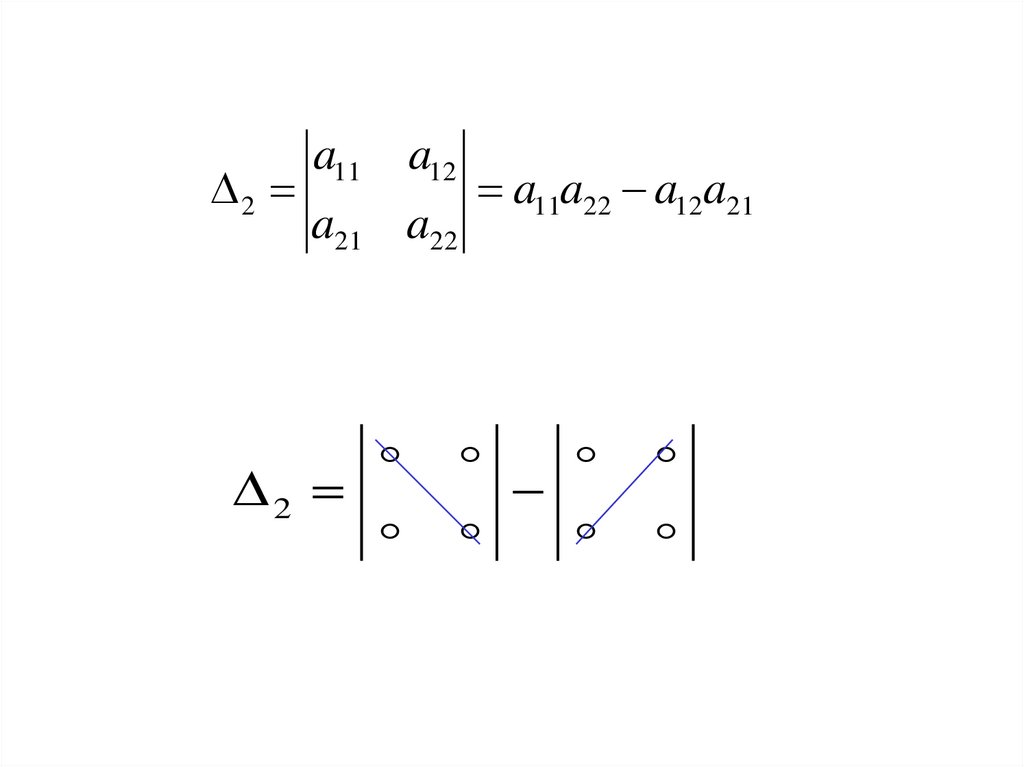


























 Математика
Математика








