Математический аппарат термодинамики. Термодинамические потенциалы. Характеристические функции

1.

Лекция 6
Математический аппарат термодинамики.
Термодинамические потенциалы. Характеристические
функции.
Различные формы записи условий термодинамического
равновесия. Критерий самопроизвольного
протекания процесса. Соотношения Максвелла и
их использование при расчетах энергии, энтальпии.

2.

Лекция 5
Второй закон термодинамики. Энтропия – функция
состояния. Изменение энтропии при необратимых
процессах. Производство энтропии.

3.

1 балл
Для реакции
3KF(тв.) +AlF3(тв) = K3AlF6(тв)
измерили тепловой эффект QV при температуре T.
Нужно посчитать энтальпию реакции ∆HT . Какую формулу
нужно использовать для самого точного расчета?
H T QV (m n) RT
H T QV
(1)
(2)
H T QV ( pV ) (3)

4.

1 балл
Простым веществом для элемента Pt служит Pt(тв). Какое из
следующих утверждений верно?
1. Энтальпия образования твердой платины при Т 298К
H f ,298 K ( Pt (тв )) 0
2. Величина С р для реакции образования твердой платины
равна нулю
3. При очень высокой температуре энтальпия образования
твердой платины H f ,Т ( Pt (тв )) отличается от нуля.
4. Величина С р для твердой платины равна нулю.

5.

1 балл
Мы знаем, что для реакции
3K(тв.) +Al (тв.) + 3F2(газ) = K3AlF6(тв)
величина ∆ср положительна.
Как меняется с температурой тепловой эффект реакции, Qp ?
Растет
(1)
Остается постоянной (2)
Трудно сказать (3)
Уменьшается (4)

6.

Первый закон термодинамики.
У любой системы существует функция состояния, называемая
внутренней энергией, U.
Второй закон термодинамики.
У любой системы существует функция состояния, называемая
энтропией, S.

7.

Полный дифференциал внутренней энергии, dU, равен:
Закрытая система
dU Q W Z
Полный дифференциал энтропии, dS, равен:
dS
Закрытая система
dS
Q
T
Q
T
dsi dsi 0
Самопроизвольный
процесс
Равновесный,
Квазистатич. процесс
; dsi 0
Система переходит из состояния 1 в состояние 2:
2
dS S
1
2
2 1
1
Q
T
2
dsi
1

8.

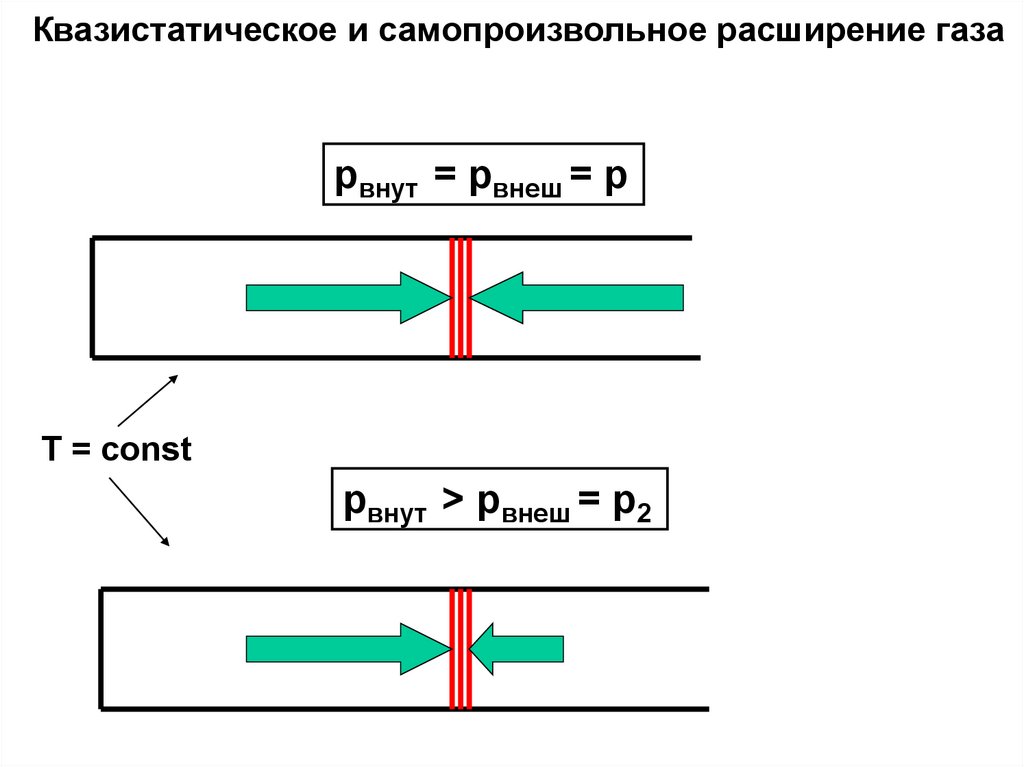
Квазистатическое и самопроизвольное расширение газа
pвнут = pвнеш = p
T = const
pвнут > pвнеш = p2

9.

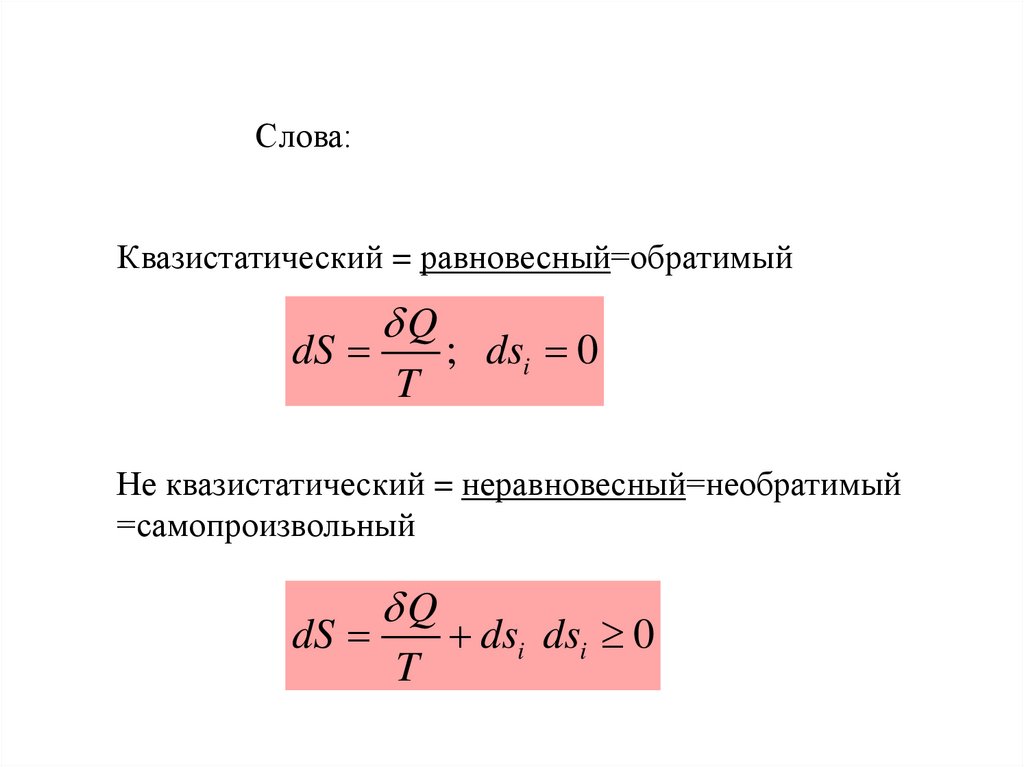
Слова:
Квазистатический = равновесный=обратимый
dS
Q
T
; dsi 0
Не квазистатический = неравновесный=необратимый
=самопроизвольный
dS
Q
T
dsi dsi 0

10.

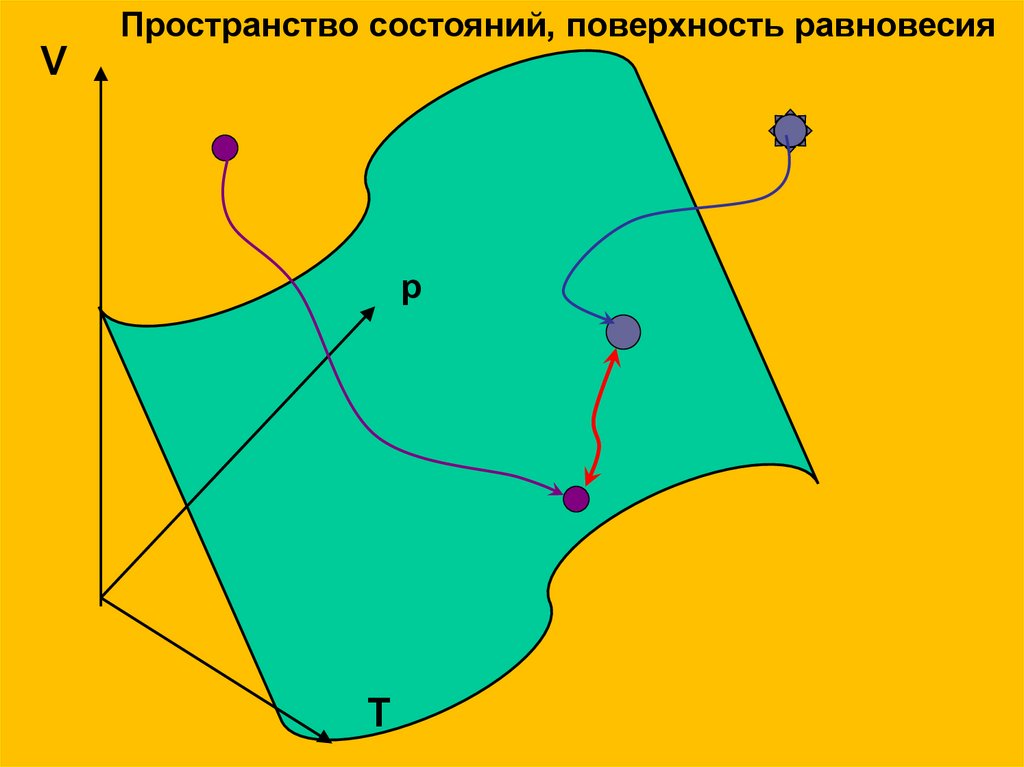
Состояния равновесия.
Это состояния, к которым самопроизвольно
стремится всякая система. Система сама не может
выйти из состояния равновесия.
(Предварительное определение)

11.

Пространство состояний, поверхность равновесия
V
p
T

12.

Выберите правильные утверждения:
2 балла
1) В любом равновесном процессе энтропия системы не
меняется.
2) В любом неравновесном процессе энтропия системы
возрастает.
3) В любом неравновесном процессе энтропия изолированной
системы возрастает.
4) Производство энтропии в системе может равняться нулю.
5) Если в системе происходят неравновесные процессы,
энтропия системы возрастает.

13.

2 балла
Какие из этих формул для энтропии, S, системы
- неправильные ?
1) dS
Q
2) dSU ,n
dsi
T
dsi
3) dSU ,V ,n dsi
4) dS 0
5) dS
Q
T
dsi 0

14.

МАТЕМАТИЧЕСКИЙ АППАРАТ ХИМИЧЕСКОЙ
ТЕРМОДИНАМИКИ
Фундаментальное уравнение

15.

ФУНДАМЕНТАЛЬНОЕ УРАВНЕНИЕ
dU Q W Z ;
dS
Q
T
(1+2 законы)
dsi Q TdS Tdsi
Z i dni
i
dU Q W Z TdS Tdsi pвнеш dV i dni
i
Равновесный процесс
dU TdS pdV i dni
i
U
U
U
T
; -p =
; i
S V ,n j
V S ,n j
ni V , S ,n j ni

16.

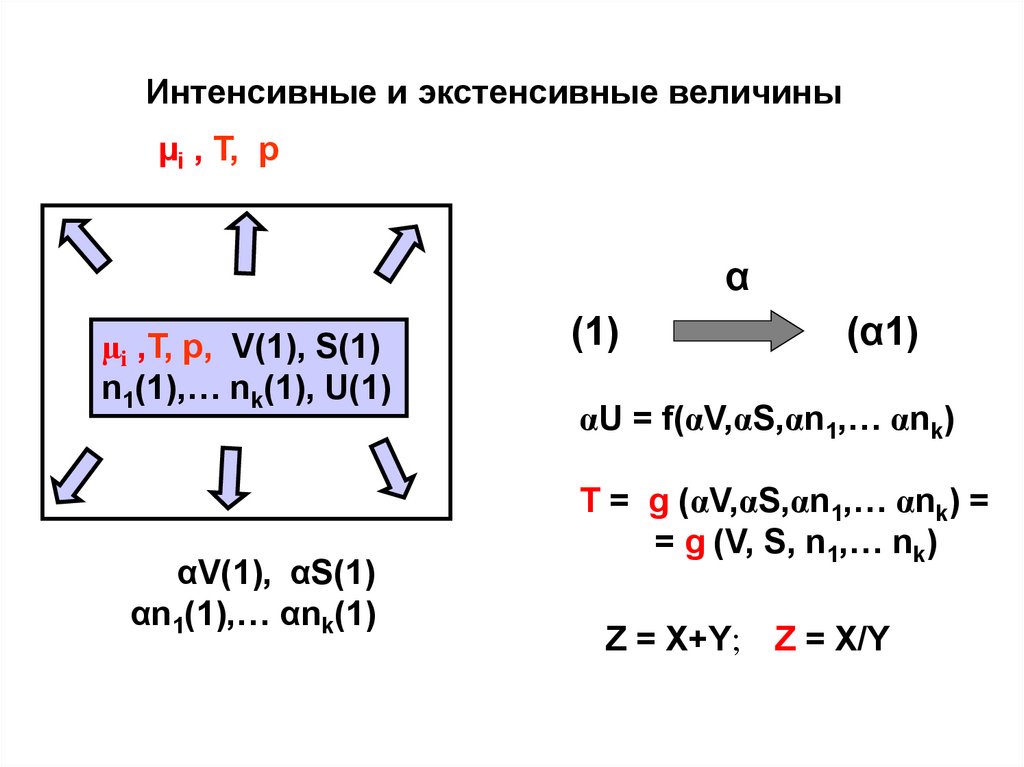
Интенсивные и экстенсивные величины
µi , T, p
α
µi ,T, p, V(1), S(1)
n1(1),… nk(1), U(1)
αV(1), αS(1)
αn1(1),… αnk(1)
(1)
(α1)
αU = f(αV,αS,αn1,… αnk)
T = g (αV,αS,αn1,… αnk) =
= g (V, S, n1,… nk)
Z = X+Y; Z = X/Y

17.

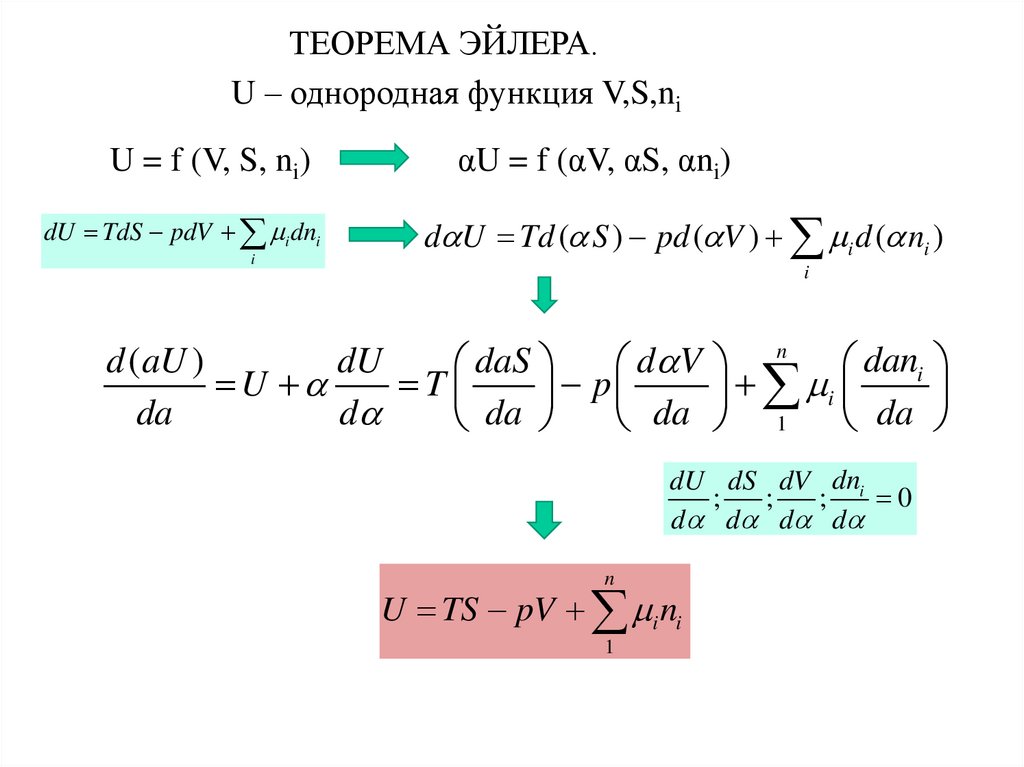
ТЕОРЕМА ЭЙЛЕРА.
U – однородная функция V,S,ni
U = f (V, S, ni)
dU TdS pdV i dni
i
αU = f (αV, αS, αni)
d U Td ( S ) pd ( V ) i d ( ni )
i
d (aU )
dU
daS
U
T
da
d
da
d V
p
da
n dani
i
da
1
dU dS dV dni
;
;
;
0
d d d d
n
U TS pV i ni
1

18.

УРАВНЕНИЕ ГИББСА-ДЮГЕМА.
dU TdS pdV 1dni
i
n
U TS pV i ni
1
dU TdS SdT pdV Vdp i dni ni d i
i
i
SdT Vdp ni d i 0;
i
p, T const ,
n d
i
i
i
0

19.

МАТЕМАТИЧЕСКИЙ АППАРАТ ХИМИЧЕСКОЙ
ТЕРМОДИНАМИКИ
Построение характеристических функций

20.

ФУНДАМЕНТАЛЬНОЕ УРАВНЕНИЕ
dU Q W Z ;
dS
Q
T
(1+2 законы)
dsi Q TdS Tdsi
Z i dni
i
Самопроизвольный процесс
dU Q W Z TdS Tdsi pвнеш dV i dni
i

21.

ФУНДАМЕНТАЛЬНОЕ УРАВНЕНИЕ
(1+2 законы)
dU Q W Z TdS Tdsi pвнеш dV i dni
i
S , V , ni const. dU S ,V ,n Tdsi 0; U min
i
TdS dU Tdsi pвнеш dV i dni
i
U , V , ni const. dS U ,V ,n dsi 0; S max
i

22.

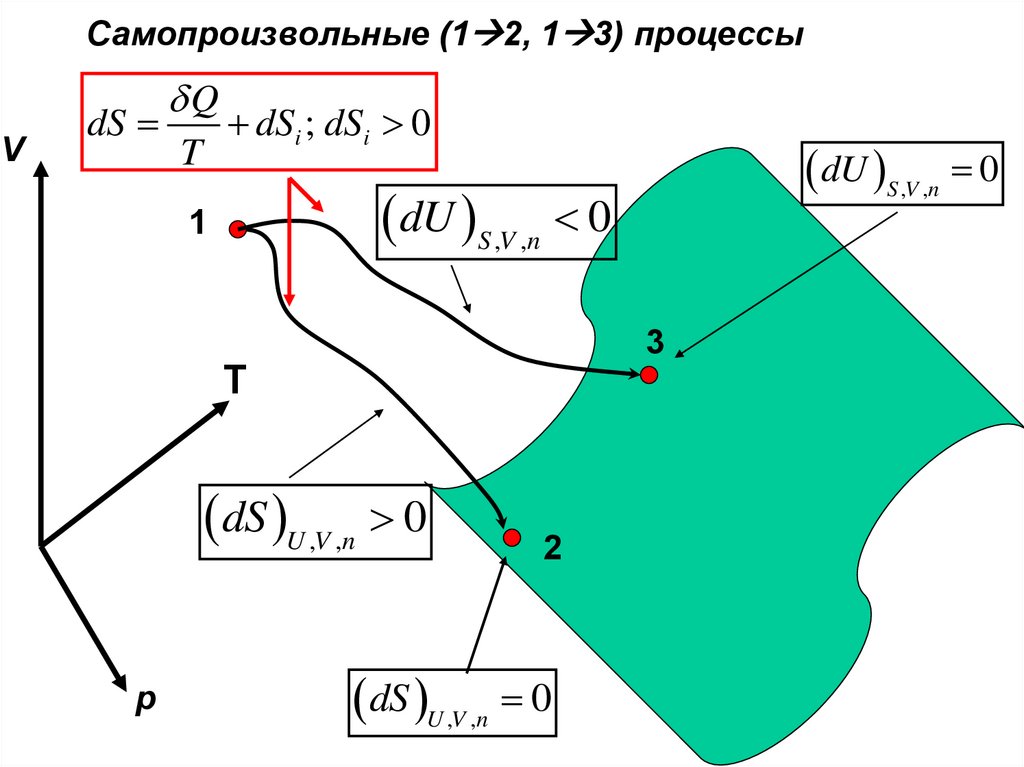
Самопроизвольные (1 2, 1 3) процессы
V
dS
Q
T
dSi ; dSi 0
dU S ,V ,n 0
dU S ,V ,n 0
1
3
T
dS U ,V ,n 0
p
2
dS U ,V ,n 0

23.

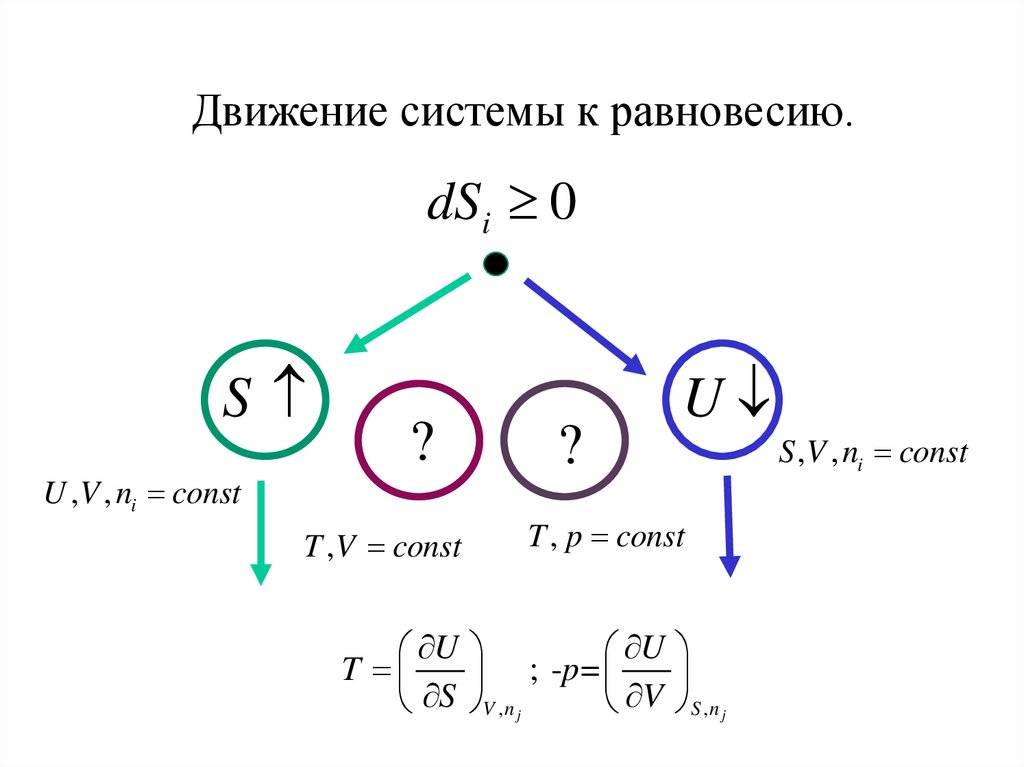
Движение системы к равновесию.
dSi 0
S
U ,V , ni const
?
T , V const
?
U
T , p const
U
U
T
; -p =
S V ,n j
V S ,n j
S ,V , ni const

24.

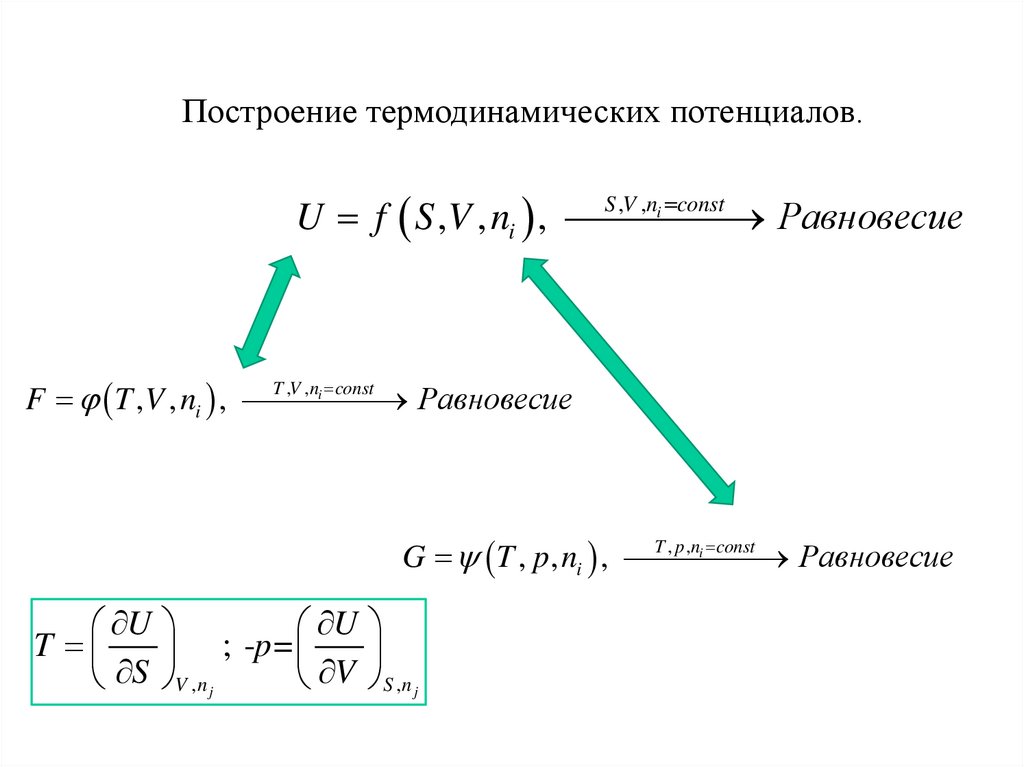
Построение термодинамических потенциалов.
S ,V ,ni const
U f S ,V , ni ,
Равновесие
T ,V ,ni const
F T ,V , ni ,
Равновесие
T , p ,ni const
G T , p, ni ,
Равновесие
U
U
T
; -p =
S
V
V ,n j
S ,n j

25.

Преобразование Лежандра
Есть функция:
f ( x)
Необходимо построить функцию:
Рецепт:
g f ' ( x) f ( x)
g f '( x) f ( x) f '( x) x
Проверка:
dg f ' ( x) df ( x) f '( x)dx xdf '( x) xdf '( x )
f ( x) sin x; g (cos x) sin x x cos x

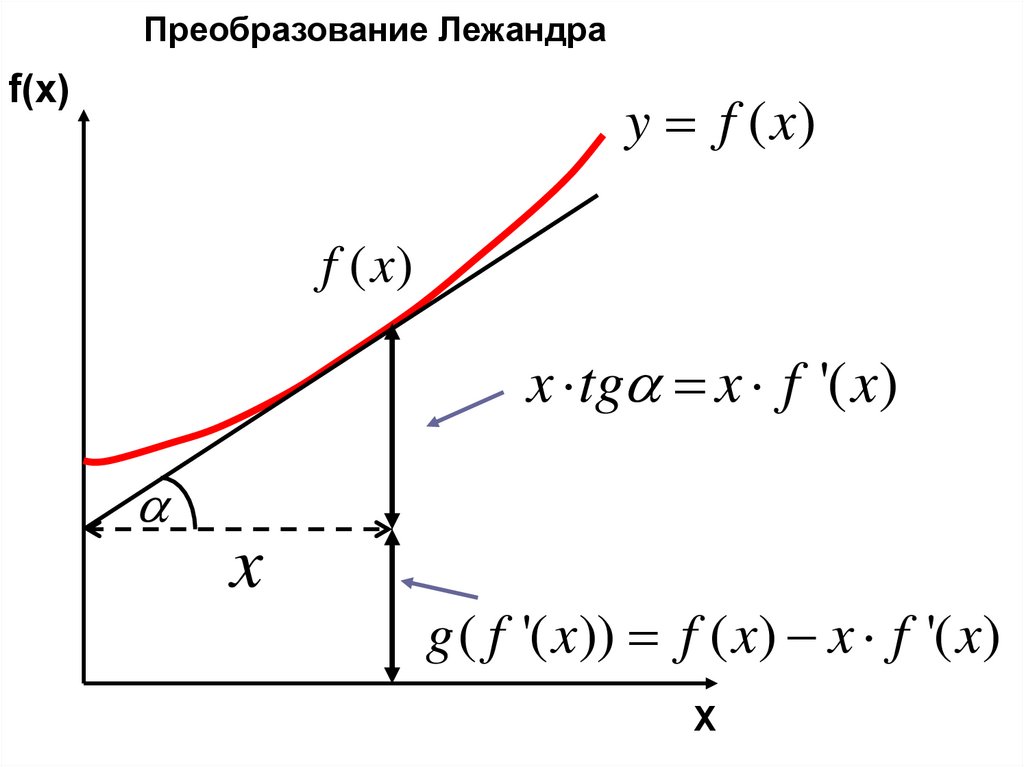
26.

Преобразование Лежандра
f(x)
y f ( x)
f ( x)
x tg x f '( x)
x
g ( f '( x)) f ( x) x f '( x)
X

27.

ПРЕОБРАЗОВАНИЕ ЛЕЖАНДРА.
U ( S ,V , ni ) F (T ,V , ni )
S
U
T
S V ,ni
U
F (T , V , ni ) U ( S , V , ni )
S U TS
S V ,ni
F U TS

28.

ПРЕОБРАЗОВАНИЕ ЛЕЖАНДРА.
U ( S ,V , ni ) G (T , p, ni )
S
U
T
S V ,ni
V
U
p
V V ,ni
U
U
G (T , p, ni ) U ( S , V , ni )
S
V U TS pV
S V ,ni
V S ,ni
G U TS pV

29.

ПРЕОБРАЗОВАНИЕ ЛЕЖАНДРА.
U ( S ,V , ni ) H ( S , p, ni )
V
U
p
V V ,ni
U
H ( S , p, ni ) U ( S , V , ni )
V U pV
V S ,ni
H U pV

30.

Как работает энергия Гиббса, G = U-TS+pV ?
Равновесный процесс
dG dU TdS SdT pdV Vdp
dU TdS pdV i dni
i
dG (T , p, ni ) SdT Vdp i dni
i
Самопроизвольный процесс
dU TdS pdV i dni Tdsi
i
dG (T , p, ni ) SdT Vdp i dni Tdsi
i
dGT , p ,ni Tdsi 0

31.

Как работают характеристические функции?
U TS pV i ni ; dU TdS pdV i dni Tdsi
i
i
dU S ,V ,ni Tdsi 0
H U pV ; dH TdS Vdp i dni Tdsi
i
dH S , p ,ni Tdsi 0
F U TS ; dF SdT pdV i dni Tdsi
i
dFT ,V ,ni Tdsi 0
G U TS pV ; dG SdT Vdp i dni Tdsi
i
dGT , p ,ni Tdsi 0

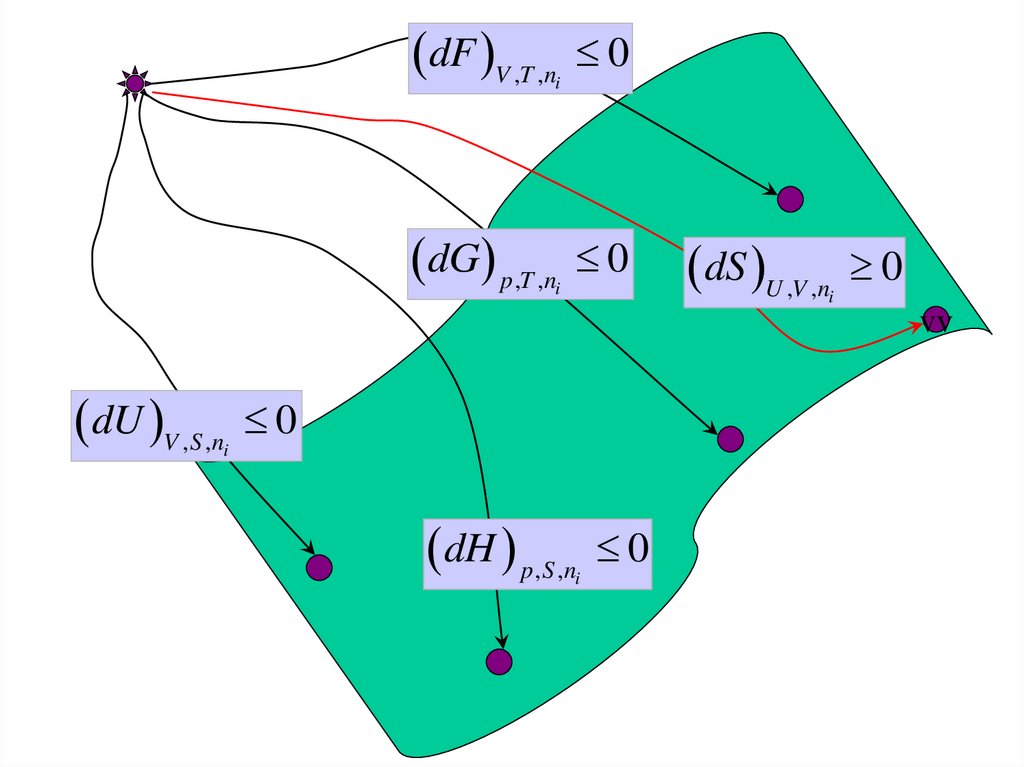
32.

dF V ,T ,n
0
dG p,T ,n
0
i
i
dS U ,V ,n
0
i
vv
dU V ,S ,n
0
i
dH p,S ,n
i
0

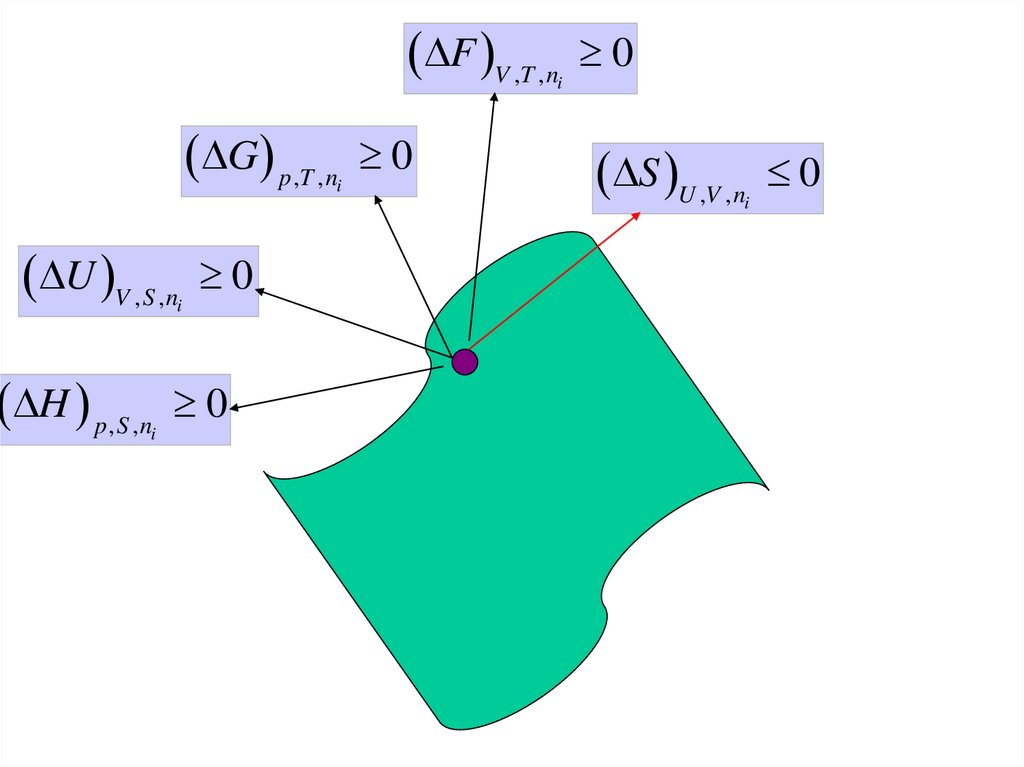
33.

F V ,T , n
0
i
G p,T , n
i
0
S U ,V , n
i
U V , S , n
0
i
H p, S , n
i
0
0

34.

МАТЕМАТИЧЕСКИЙ АППАРАТ ХИМИЧЕСКОЙ
ТЕРМОДИНАМИКИ
Соотношения Максвелла

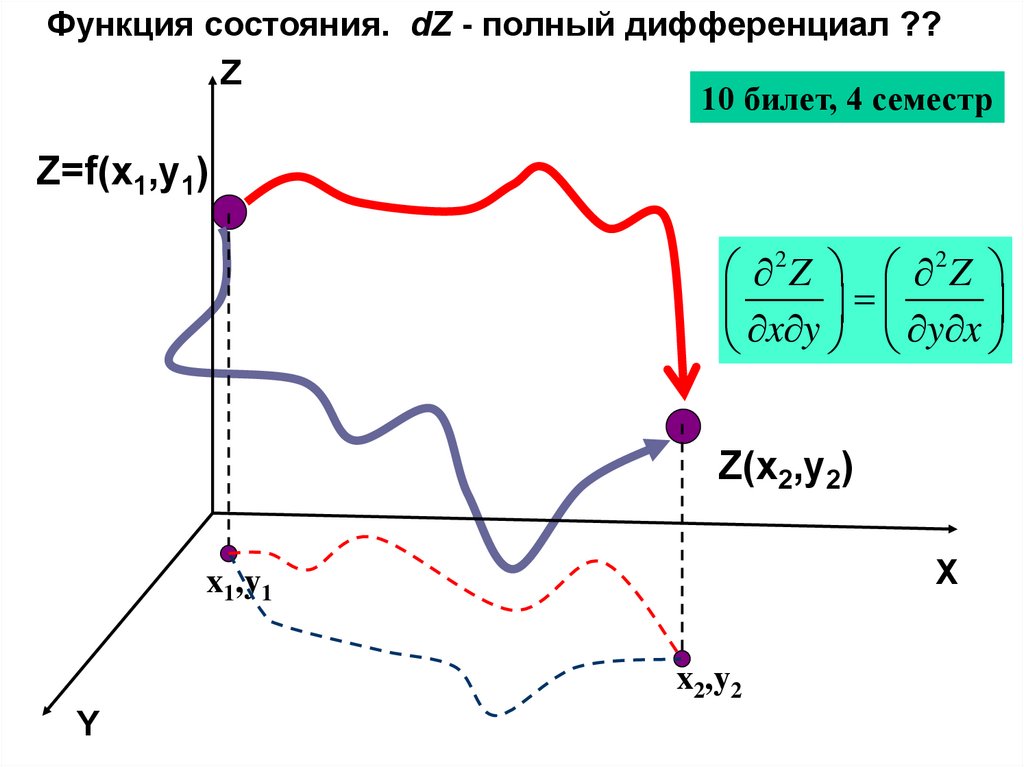
35.

Функция состояния. dZ - полный дифференциал ??
Z
10 билет, 4 семестр
Z=f(x1,y1)
2Z 2Z
x y y x
Z(x2,y2)
X
x1,y1
x2,y2
Y

36.

Соотношения Максвелла
dF SdT pdV i dni
i
2F
T V
2F
V T
S
p
V
T
V ,ni
T ,ni
dG SdT Vdp i dni
i
2G 2G
T p p T
S
V
p
T
p ,ni
T ,ni

37.

Внутренняя энергия идеального газа при T =const не зависит
от объема?
dU TdS pdV ;
U
S
T
p
V T
V T
Используем соотношение Максвелла !
U
S
T
p;
V T
V T
RT
V
R
S p
V
T
T
V
T
V
V
RT
U
S
p 0
T
p
V
V T
V T

38.

Энтальпия идеального газа при T=const не зависит от давления?
dH TdS Vdp;
H
S
T V
p T
p T
Используем соотношение Максвелла !
H
S
T
V ;
p T
p T
RT
S
p
V
p
T
p
T
T
R
p
p
V
H
RT
V 0
T
V
p
T p
p T

39.

ХИМИЧЕСКИЙ ПОТЕНЦИАЛ, μi

40.

Определения химического потенциала
dU TdS pdV i dni ;
i
dH SdT Vdp i dni ;
i
dF SdT pdV i dni ;
i
dG SdT Vdp i dni ;
i
U
i
ni S ,V ,n j i
H
i
ni S , p ,n j i
F
i
ni T ,V ,n j i
G
i
ni T , p ,n j i

41.

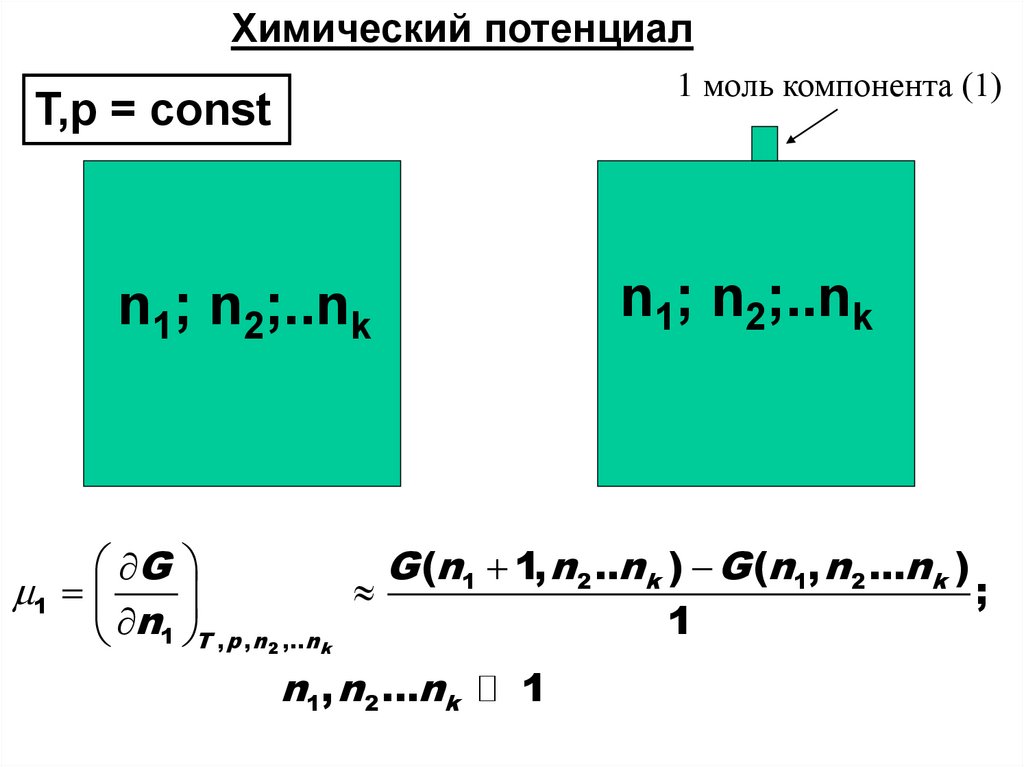
Химический потенциал
1 моль компонента (1)
T,p = const
n1; n2;..nk
n1; n2;..nk
G
G (n1 1, n 2 ..nk ) G (n1, n 2 ...nk )
1
;
1
n1 T , p ,n2 ,..nk
n1, n 2 ...nk
1

42.

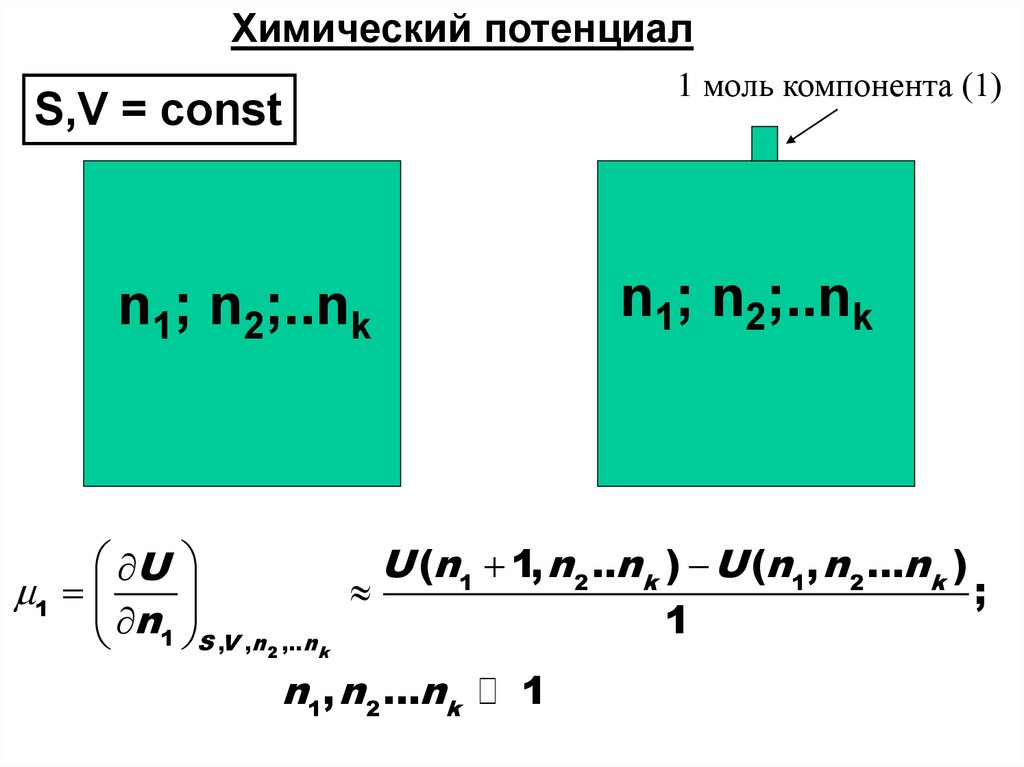
Химический потенциал
1 моль компонента (1)
S,V = const
n1; n2;..nk
n1; n2;..nk
U
U (n1 1, n 2 ..n k ) U (n1, n 2 ...n k )
1
;
1
n1 S ,V ,n2 ,..nk
n1, n 2 ...nk
1

43.

Химический потенциал
U TS pV i ni ; G U TS pV
i
G i ni
i
n1 1; n2 ,.....ni 0; G 1

44.

Химический потенциал идеального газа
n1 1; G 1 ; d SdT Vdp
(T const ; p 1, бар)
0
0
T
p
p
(T const ; p ) Vdp
0
T
0
T
p0
p0
RT
p
0
dp T RT ln 0
p
p

45.

Химический потенциал реального газа
p
p
(T const ; p ) Vdp
0
T
0
T
p0
p0
RT
p
0
dp T RT ln 0
p
p
p
(T const ; p ) T0 Vdp ???
p0
f ( p, T )
T RT ln
0
p
0
T

46.

Химический потенциал идеального и реального газа
p
ид. (T ; p) (T ) RT ln 0
p
0
f ( p, T )
реал (T , p ) (T ) RT ln
0
p
0