Термодинамические функции состояния

1.

ПОВТОРЕНИЕ:
ТЕРМОДИНАМИЧЕСКИЕ
ФУНКЦИИ
СОСТОЯНИЯ

2.

Разбор домашнего задания
MnV MVp
m0
,
NA
N A kT
RT
v
,
MN A p
MV p
MV T L
M pV TL
m
T
RT
2 3
RT T
RT Tv v
RT
2
Mp

3.

Разбор домашнего задания
p
L
1 p
LM
2
T
p T RT
RT
T
Mp
LM
LM
ln p ln C
P C exp
RT
RT

4.

Разбор домашнего задания
T2
L(m2 m1 )
S
c p m2 ln
T2
T1

5.

Проверочная работа

6.

gг pп , T gж pк , T
g ж
g ж pк , T g ж p, T
p
к
pк p
T p p
к
g ж
V0
dG Vdp SdT dg vdp sdT
pк T M
V0 2
g ж pк , T g ж p, T V0 pк p
M r

7.

dG Vdp SdT dg T vdp
RT
RT pп
g г pп , T g г p, T vdp
dp
ln
Mp
M p
p
p
pп
pп
V0 2 RT pп
2
ln pп p exp V0
M r
M p
rRT
Для капель воды с r = 10-5см давление р1 всего
на 1 % больше, чем р. Для капель размером г =
10-6 см разница давлений уже около 10 %.

8.

Еще раз о законе сохранения
энергии
dU 0
Макс Планк :
B
dU U
A
B
U A

9.

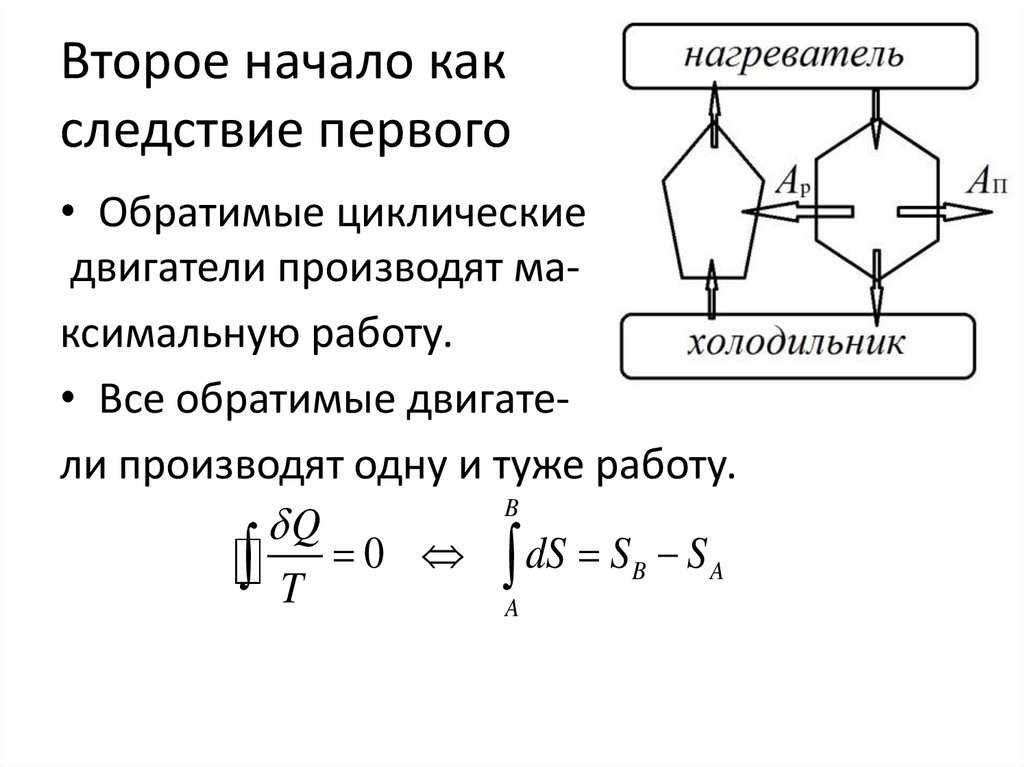
Второе начало как
следствие первого
• Обратимые циклические
двигатели производят максимальную работу.
• Все обратимые двигатели производят одну и туже работу.
B
Q
T 0 A dS SB S A

10.

Различные формулировки
Q
T 0 dS 0

11.

Свободная энергия (потенциал
Гельмгольца)
F U TS; d F TdS pdV TdS SdT
pdV SdT ; F V,T
F
dF
V
F
V
F
T
T
F
dV
T
T
F
p,
T
dT ;
V
S ;
V
pdV A

12.

Экстремальные свойства свободной
энергии
• Неравенство Клаузиуса: в самопроизвольных процессах
TdS Q dU pdV
• Определение F U TS
• Дифференциал при постоянстве естественных переменных
dF V ,T d U TS V ,T dU pdV TdS V ,T 0

13.

Энтальпия (теплосодержание)
H U pV ; dH dU pdV Vdp TdS pdV
pdV Vdp TdS Vdp; H S, p
H
H
dH
dS
dp;
S p
p S
H
H
T,
V;
S p
p S
H p TdS Q

14.

Экстремальные свойства свободной
энергии
• Неравенство Клаузиуса: в самопроизвольных процессах
TdS Q dU pdV
• Определение H U pV
• Дифференциал при постоянстве естественных переменных
dH S , p d U pV S , p dU pdV Vdp TdS S , p 0

15.

V0
T
q
r
T

16.

dg vdp sdT
gг p, T gж p, T
gг p, T gж pк , T
g г
g ж
g ж
T T pk p T T
T
p
T
g г
g ж
g ж 2
T T T T
T
T
p r
2 V0
2 V0T
2
T
sг sж T T V0
r
r sг sж
rq

17.

1
2
S

18.

dU pdV
dS
T
dV
V
dS u R
S u R ln
V
V0
V1 V2
V1 V2
S S1 S2 1R ln
2 R ln
V1
V2
1 2
1 2
1 R ln
2 R ln
0
1
2

19.

Парадокс Гиббса
Пусть 1= 2= S 2 R ln 2

20.

21.

Будем следить за фронтом выравнивания давления
p1V1
V1 p2V2
V2
S S1 S2
R ln
R ln
T1
V1 T2
V2
p1V1
p1 p2V2
p2
R ln
R ln
T1
p T2
p
p1V1 pV1 , p2V2 pV2 , V1 V2 V1 V2
p1V1 p2V2
p
V1 V2

22.

Связь с работой
системы
0
0

23.

Связь с работой системы
dU pdV
dV
dT
dS
cv
R
T
V
T
T
V
S cv ln R ln
T0
V0
2
2
T
V
S S1 S2 cv ln
R ln
0
TATB
VAVB
VA VB
2V
2nV
V
, VA
, VB
2
n 1
n 1

24.

n 1
V
V
VAVB 2V 2nV
4n
n 1 n 1
2
2
T
V
4n
cv ln
R ln
R ln
2
TATB
VAVB
n 1
2
2
2
4
n
T 2 T02 n
2
n 1
R
cv
R
cv
4n
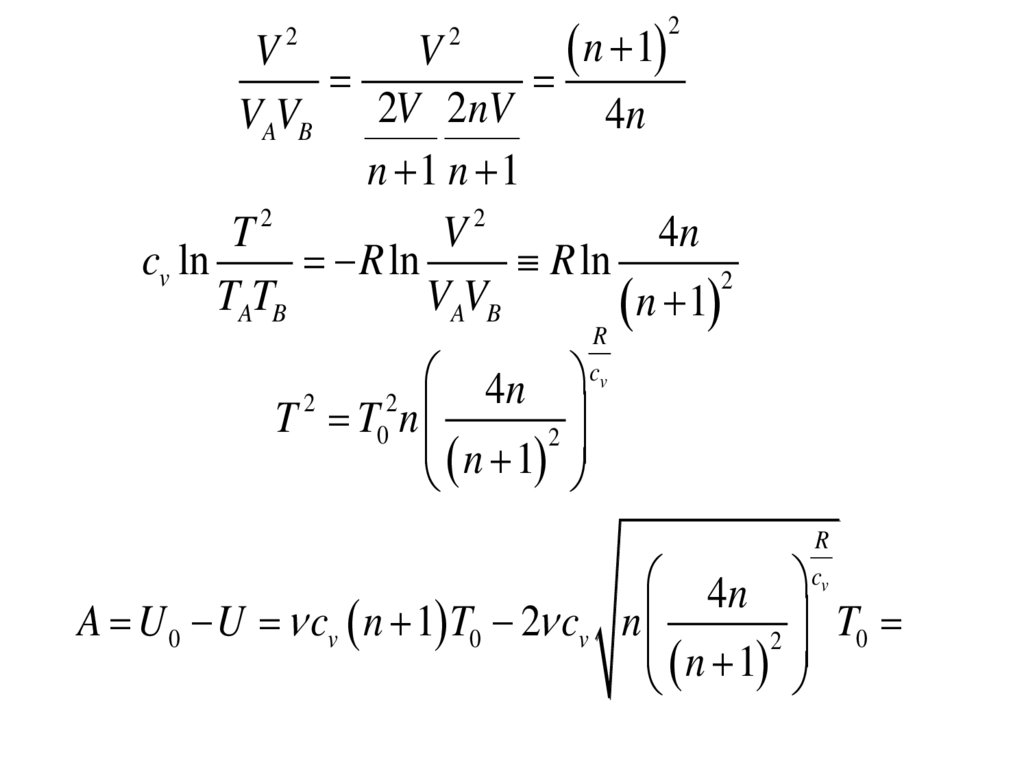
A U 0 U cv n 1 T0 2 cv n
T0
2
n 1

25.

1
3
4n
3
RT0 n 1 n
2
n 1
2

26.

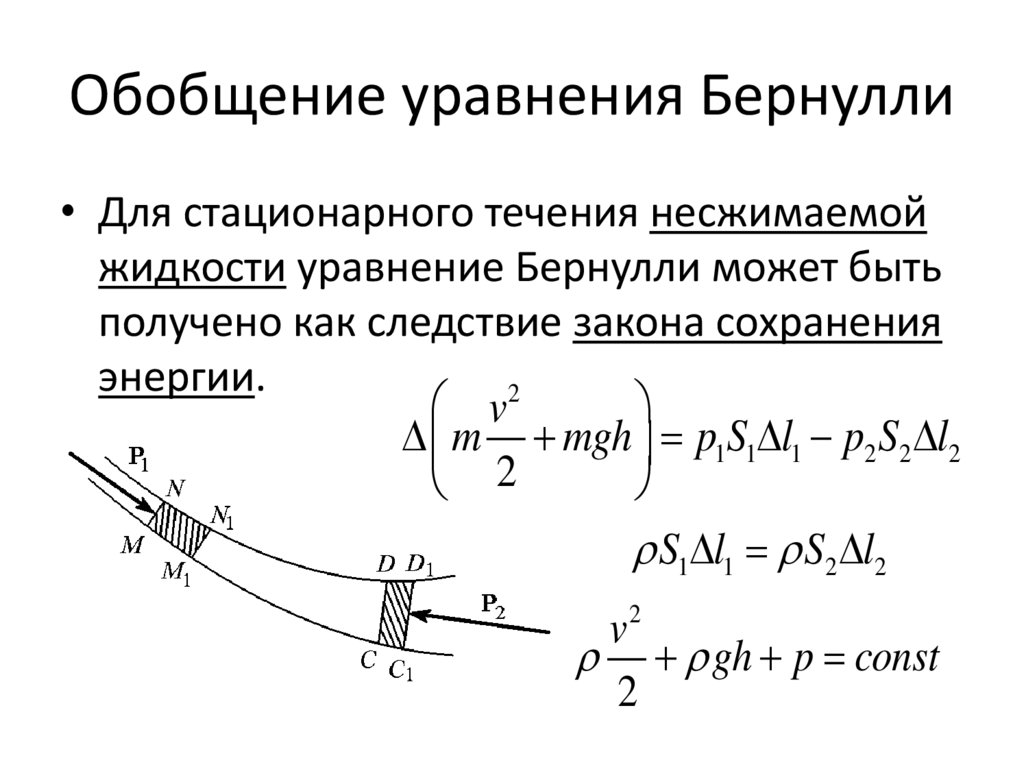
Обобщение уравнения Бернулли
• Для стационарного течения несжимаемой
жидкости уравнение Бернулли может быть
получено как следствие закона сохранения
энергии.
v2
m mgh p1S1 l1 p2 S2 l2
2
S1 l1 S2 l2
v2
gh p const
2

27.

Сжимаемая среда
m 2 m 1 p1S1 l1 p2 S2 l2
p1 p2
2 1
m 1S1 l1 2 S2 l2
1 2
p2 p1
2 1 const
2 1

28.

Сжимаемая среда
m 2 m 1 p1S1 l1 p2 S2 l2
p1 p2
2 1
m 1S1 l1 2 S2 l2
1 2
p2 p1
2 1 const
2 1
Закон сохранения энтальпии
U
U pV const
u
m