Введение. Кинематика поступательного и вращательного движения вопросы

1.

Карбань Оксана Владиславовна,
заведущая кафедры “Физика”, д.ф.-м.н
1 семестр – Механика и молекулярная
физика
2 семестр – Электричество и магнетизм
3 семестр - Оптика и квантовая физика
Литература: Трофимова Т. И.
Курс физики: учеб. пособие для вузов /— 11-е
изд., стер. — М.: Издательский центр Академия,
2006. — 560 с.

2.

Виды занятий:
Лекции – 1 раз в неделю
Практика – 1 раз в неделю с 5
октября!!!!
Лабораторные работы – 1 раз в две
недели по подгруппам
Каждая лекция – отдельная тема!
Каждая практика – задачи на отдельную тему.
Не повторяются!
Форма оценки в I семестре - зачет

3.

Условие получение автомата
1. Пропуск не более 2 лекций
2. Закрыть лабораторные работы к моменту
зачета
3. Отсутствие неудовлетворительных
оценок за контрольные
4. Сдача РГР до 20 декабря
Контрольные:
2 промежуточные контрольные
Отработки долгов – консультации

4. Лекция № 1

Введение. Кинематика
поступательного и
вращательного движения
вопросы

5.

Физика – это наука, изучающая наиболее общие
законы, которым подчиняется окружающий нас
внешний мир.
Механика, рассматривающая движение
объектов, превышающих размеры
атомов, перемещающихся со скоростями
много меньшими скорости света
Молекулярная физика и
термодинамика, занимающиеся
изучением теплоты, температуры
и поведения систем, состоящих из
большого числа частиц

6.

Электромагнетизм, изучающий взаимодействие
электрических зарядов и электромагнитных полей
Оптика, анализирующая
поведение света, и его
взаимодействие с
различными материалами.

7.

Квантовая физика,
содержащая теории поведения
объектов микроскопических
размеров.
Международная система единиц (СИ)
фр. SystèmeInternational
Метр Килограмм
Секунда
Ампер Кельвин Моль
Кандела Радиан Стерадиан
Гауссова система единиц (СГС)
«сантиметр –грамм –секунда

8.

Механика — раздел физики, который изучает
закономерности механического движения и
причины, вызывающие или изменящие это
движение.
Механика Галилея-Ньютона наз-ся
классической механикой.
Законы движения макроскопических тел,
скорости к-рых малы по сравнению со
скоростью света.
Механика Эйнштейна и
квантовая

9.

Релятивистская механика, основана на cпециальной
теории относительности, сформулированной А.
Эйнштейном
Законы движения макроскопических тел со
скоростями, сравнимыми со скоростью света
Кинематика изучает движение тел, не расм-ая
причины, к-рые это движение обусловливают
Механическое движение

10.

Мех-кое движение — это изм-ние с течением
времени взаимного расположения тел или их
частей в пространстве.
При поступательном дв-нии все
точки тела движутся одинаково,
имеют одинаковые скорости и
ускорения.
При вращательном движении все
точки тела движутся по окружностям,
центры, к-ых лежат на одной
прямой, наз-ой осью вращения.
Материальной точкой наз-ся тело, формой и
размерами к-го можно пренебречь по сравнению с
Система отсчета,
расстоянием, на к-ом оно рассматривается
система координат

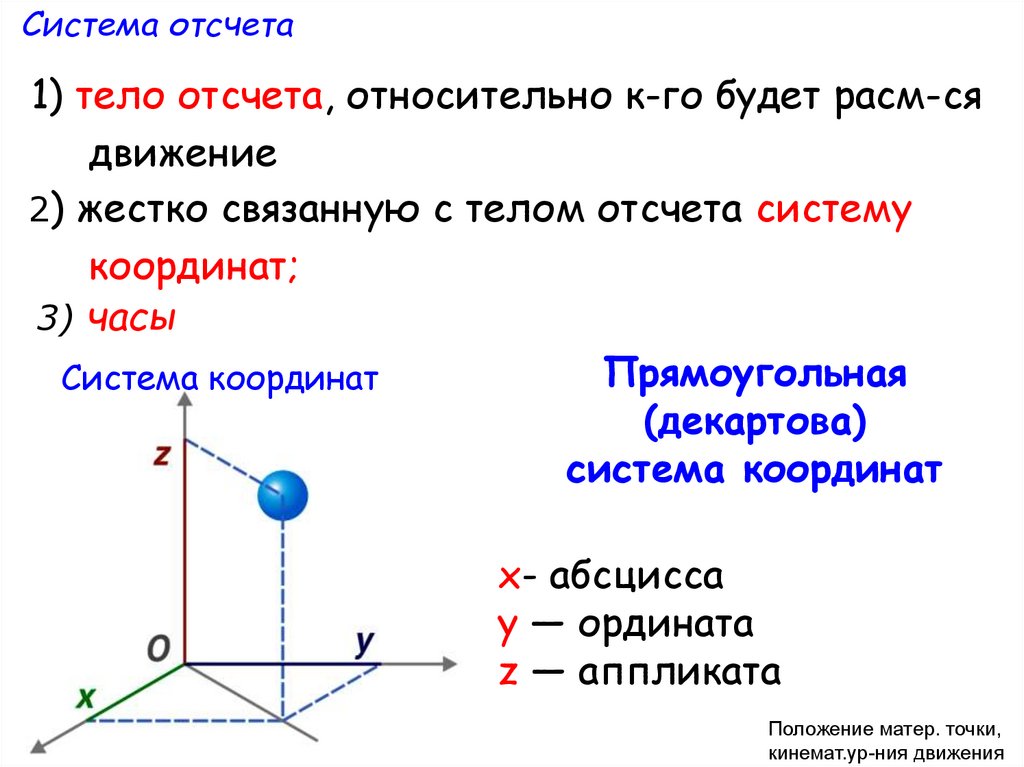
11.

Система отсчета
1) тело отсчета, относительно к-го будет расм-ся
движение
2) жестко связанную с телом отсчета систему
координат;
3) часы
Прямоугольная
Система координат
(декартова)
система координат
х- абсцисса
y — ордината
z — аппликата
Положение матер. точки,
кинемат.ур-ния движения

12.

1) Координатный - тремя
координатами (X,Y,Z)
2) Векторный - радиус вектором r,
проведенным из начала системы
координат в ту точку, где в данный
момент времени находится тело.
Кинематические
уравнения движения
x x (t )
y y (t )
z z (t )
r r t
r xi yj zk
Связь координатного
и векторного способа
Одномерное - вдоль прямой, двумерное - на
плоскости, многомерное – в пространстве
Траектория, путь

13.

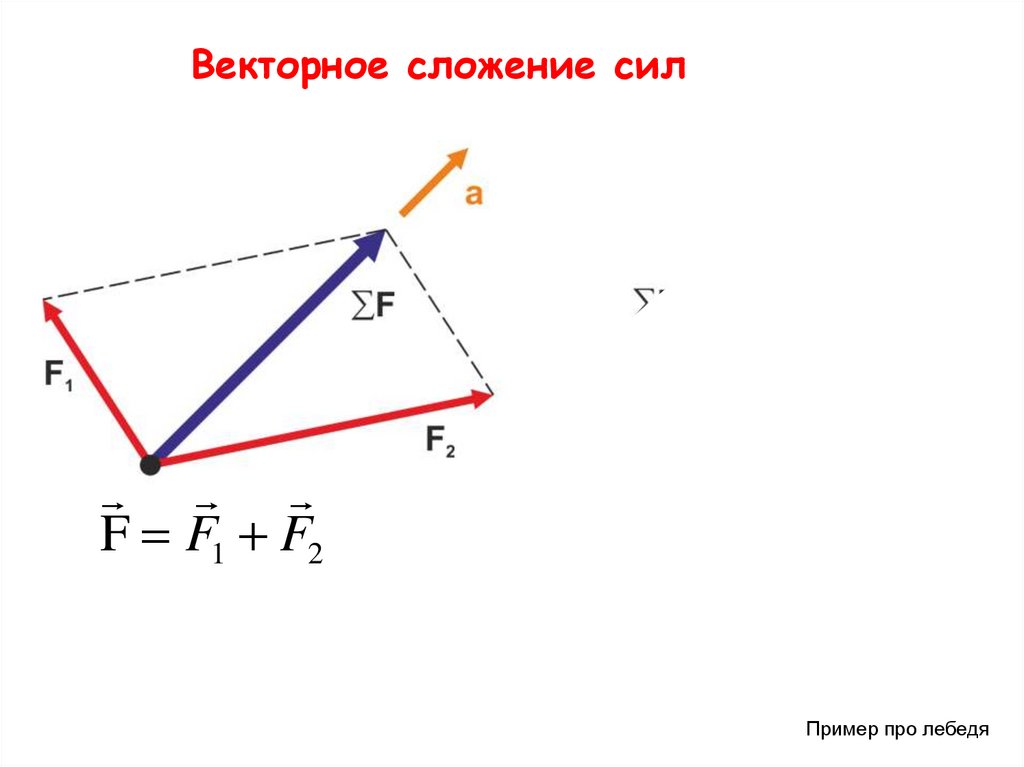
Векторное сложение сил
F1 F2
F F1 F2
F F1 F2 F3
Пример про лебедя

14.

Тест 1
Лебедь
F=0
Рак
Щука
1
8
2
7
3
6
4
5

15.

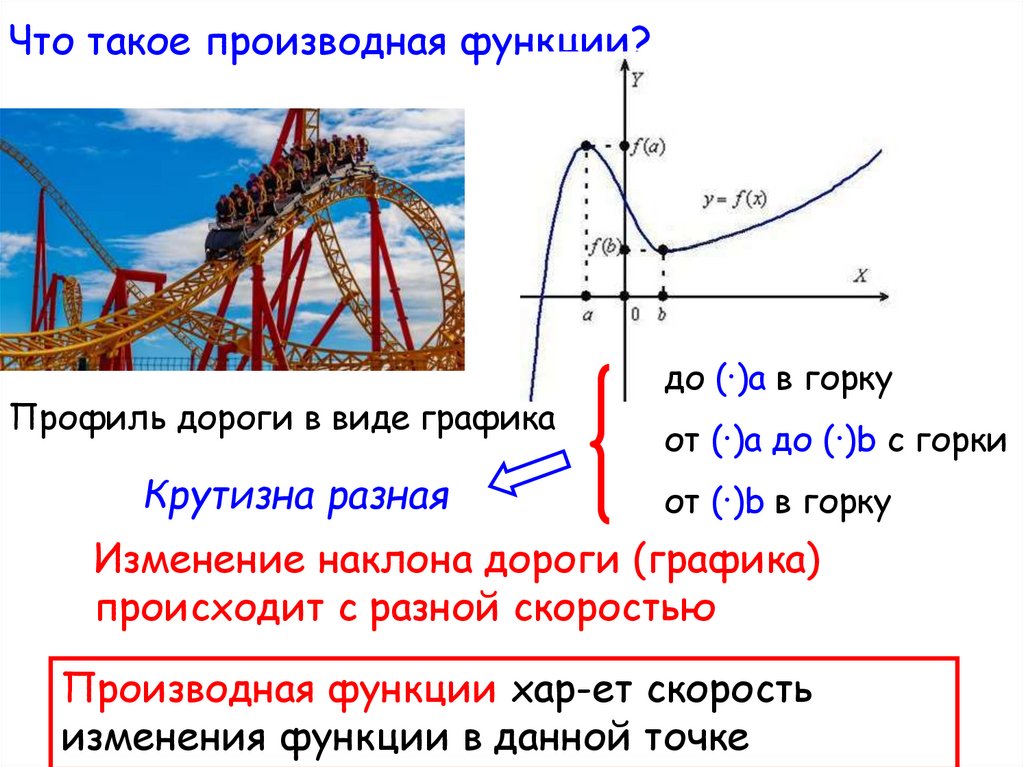
Что такое производная функции?
Профиль дороги в виде графика
Крутизна разная
до (·)a в горку
от (·)a до (·)b с горки
от (·)b в горку
Изменение наклона дороги (графика)
происходит с разной скоростью
Производная функции хар-ет скорость
изменения функции в данной точке

16.

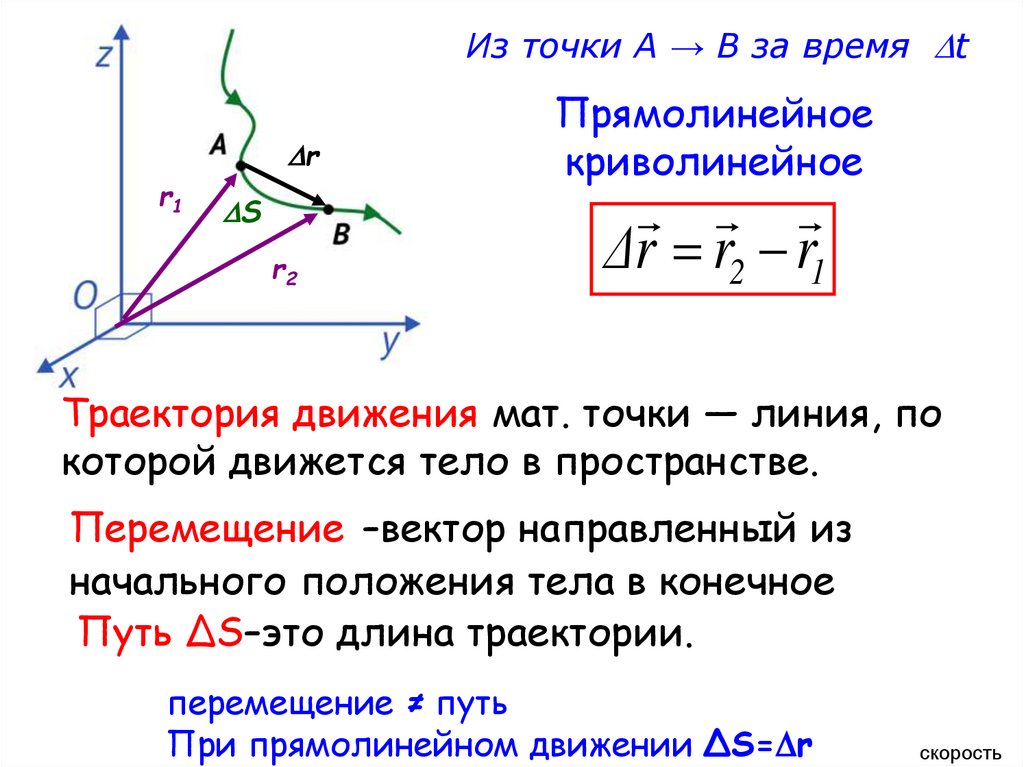
Из точки А → В за время t
r
r1
S
r2
Прямолинейное
криволинейное
Δr r2 r1
Траектория движения мат. точки — линия, по
которой движется тело в пространстве.
Перемещение –вектор направленный из
начального положения тела в конечное
Путь ΔS–это длина траектории.
перемещение ≠ путь
При прямолинейном движении ΔS= r
скорость

17.

Скорость - это физическая величина,
которая определяет как быстроту
движения, так и его направление в
данный момент времени
ср
r
t
ср r
– средняя скорость за
время t
t→0
ΔS r
r dr
lim
dt
t 0 t
r
S dS
lim
lim
t
dt
t 0 t
Модуль мгновенной скорости
равен первой производной
пути по времени
t 0
[ ] —
метр в секунду
(м/с).
Равномерн.двние, ускорение

18.

x y z x i y j z k
dх
х
dt
dy
у
dt
dz
z
dt
Как найти путь?
Геометрический
смысл -площадь под
кривой (t) есть
путь тела за время t
Равномерное движение – движение с постоянной
скоростью
t2
t2
t1
t1
S dt dt (t2 t1 ) t
S t
ускорение

19.

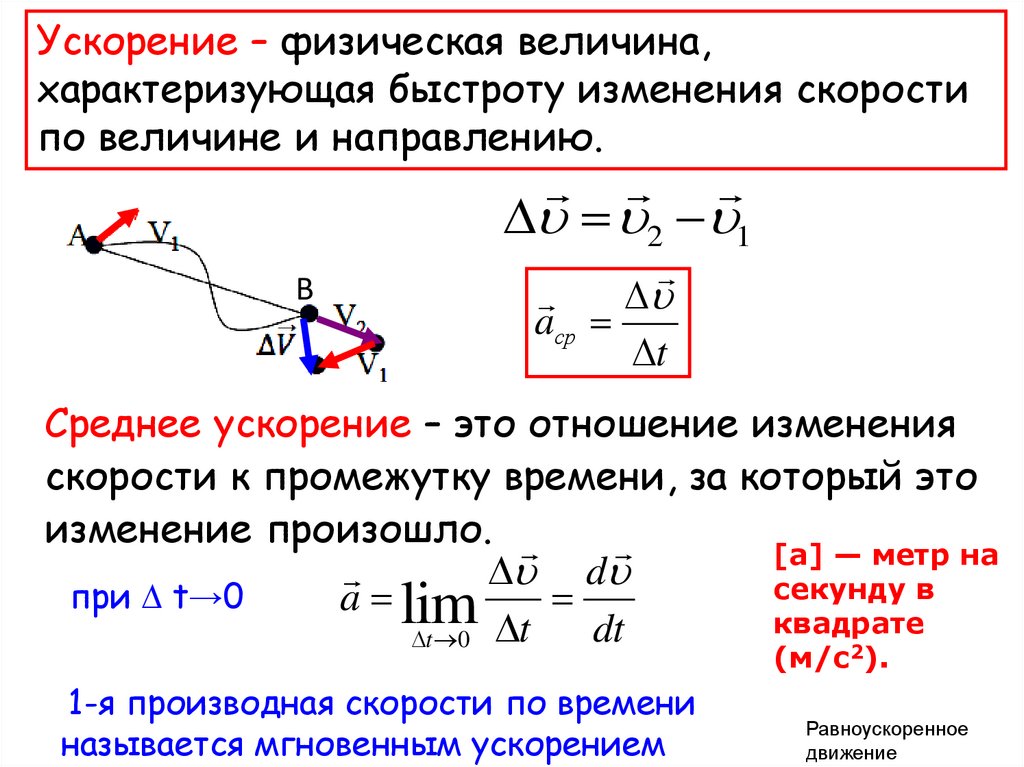
Ускорение – физическая величина,
характеризующая быстроту изменения скорости
по величине и направлению.
2 1
В
aср
t
Среднее ускорение – это отношение изменения
скорости к промежутку времени, за который это
изменение произошло.
[a] — метр на
d
секунду в
при t→0
a lim
квадрате
dt
t 0 t
2
(м/с ).
1-я производная скорости по времени
называется мгновенным ускорением
Равноускоренное
движение

20.

Равноускоренное движение – движение с
постоянным ускорением.
0 at
a const
dS
2
d
d
S
dt
a lim
lim
2
dt
dt
dt
t 0 t
t 0 t
Ускорение -2-я производная пути по времени
t
t
S dt 0 at dt 0t at / 2
2
0
0
Путь при равноускоренном движении
пример

21.

Равномерное а=0
равноускоренное
равнозамедленное
Разложение ускорений

22.

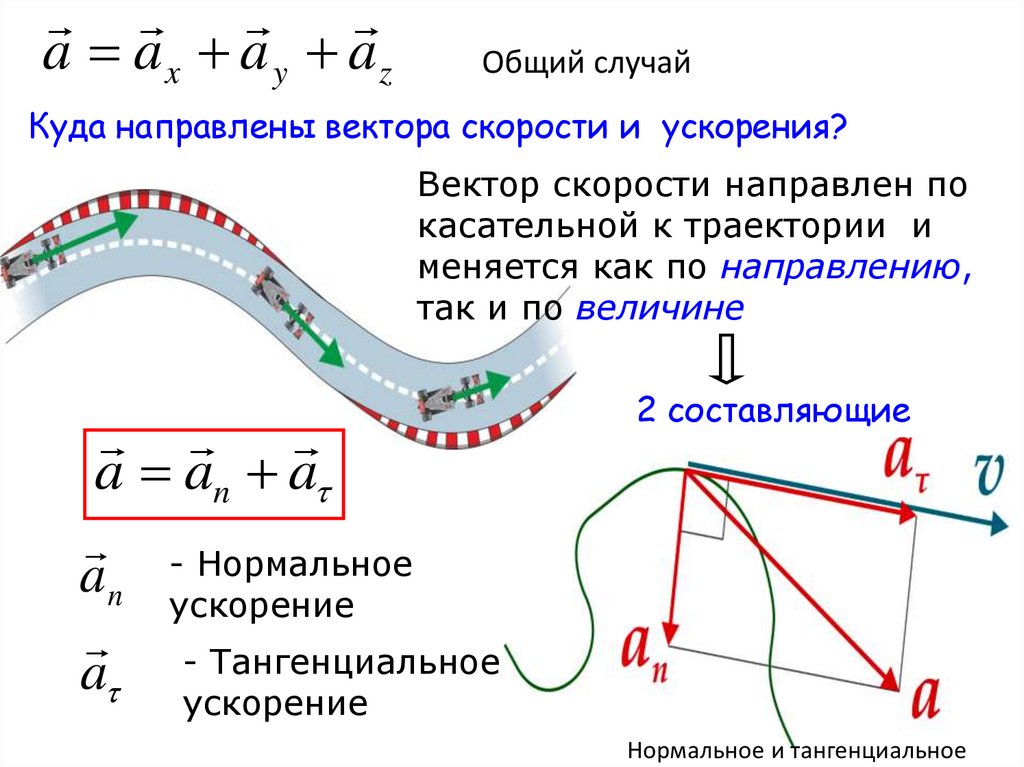
a ax a y az
Общий случай
Куда направлены вектора скорости и ускорения?
Вектор скорости направлен по
касательной к траектории и
меняется как по направлению,
так и по величине
a an a
- Нормальное
a n ускорение
- Тангенциальное
a ускорение
2 составляющие
Нормальное и тангенциальное

23.

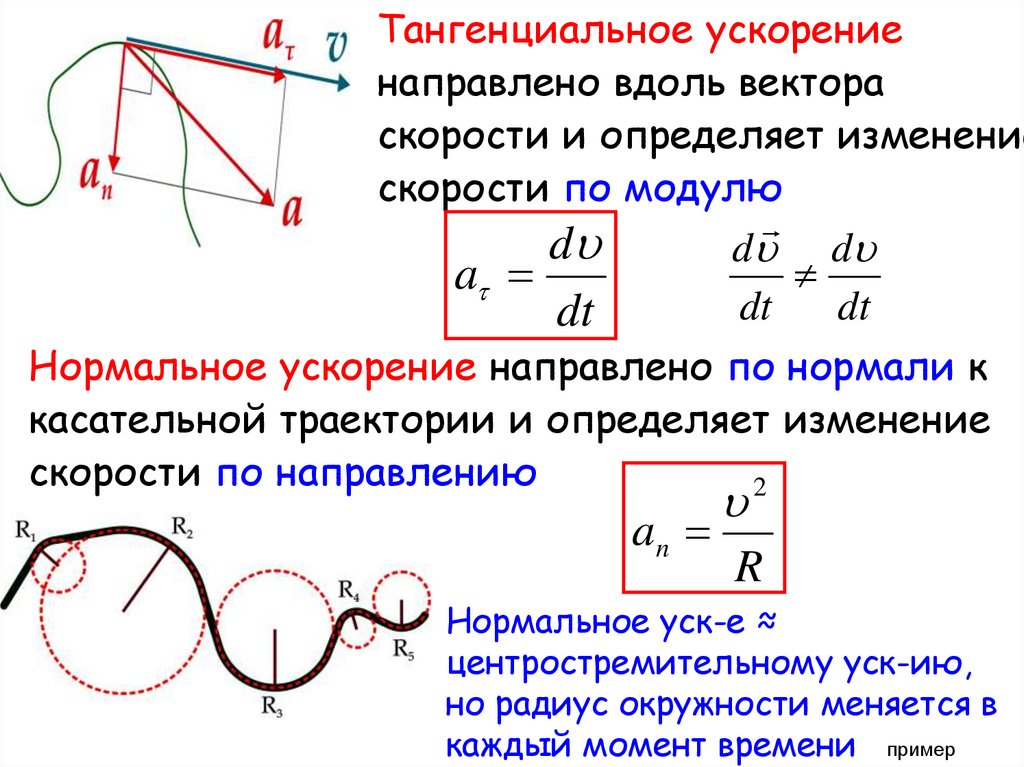
Тангенциальное ускорение
направлено вдоль вектора
скорости и определяет изменение
скорости по модулю
d
d d
a
dt
dt
dt
Нормальное ускорение направлено по нормали к
касательной траектории и определяет изменение
скорости по направлению
2
an
R
Нормальное уск-е ≈
центростремительному уск-ию,
но радиус окружности меняется в
каждый момент времени пример

24.

Тест 1.
Мат. точка вращается по окружности со
скоростью v(t). Начальный момент
В наблюдения соответствует времени А. В
каком направлении в момент времени В
будут направлены векторы ?
А
1. Скорости?
2. Тангенциального
ускорения?
1
8
2
7
3
6
4
5
5
3. Нормального
ускорения?
4. Перемещения? 2
5
7

25.

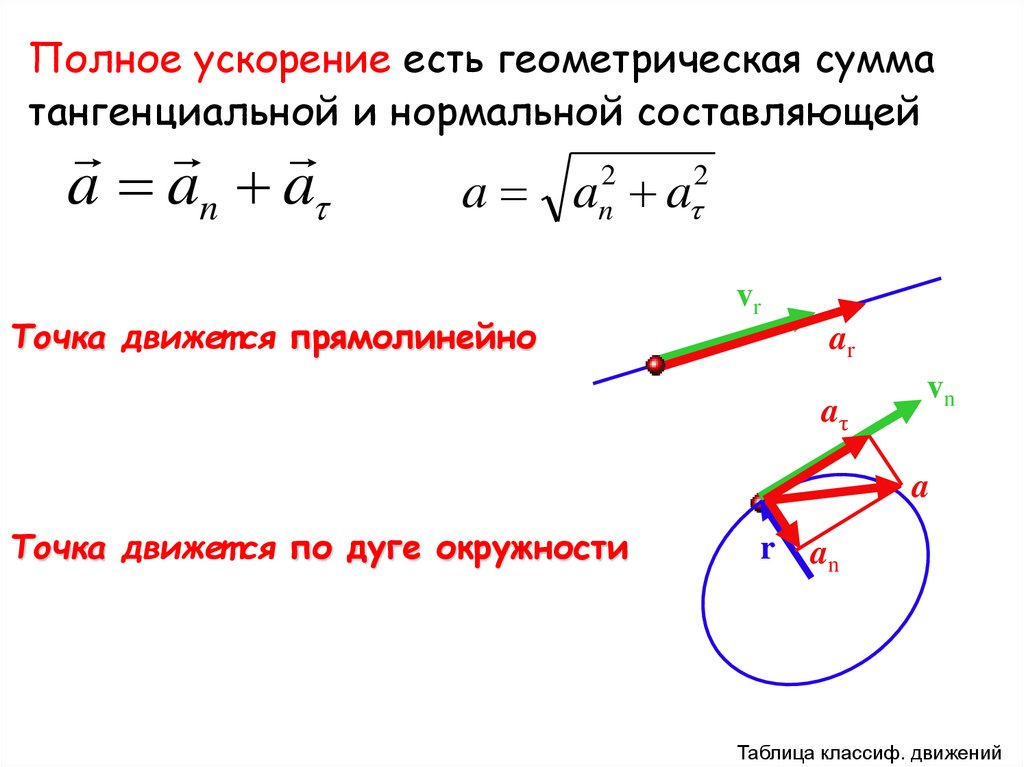
Полное ускорение есть геометрическая сумма
тангенциальной и нормальной составляющей
a an a
a a a
2
n
Точка движет ся прямолинейно
2
vr
ar
aτ
vn
a
Точка движет ся по дуге окружности
r
an
Таблица классиф. движений

26.

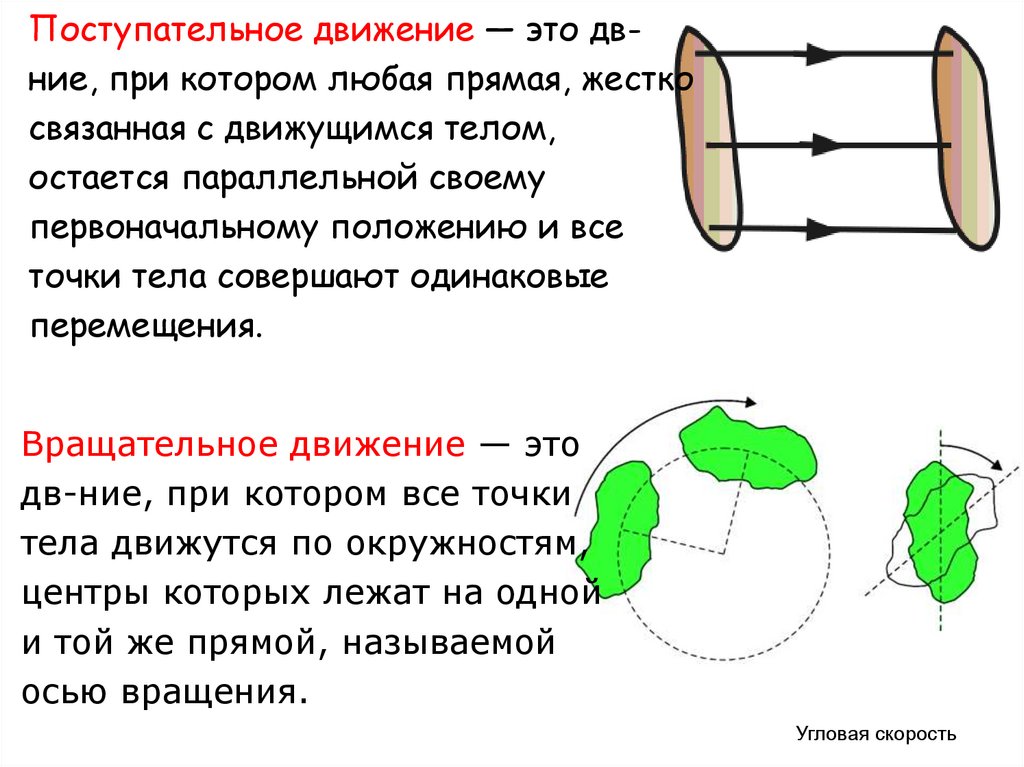
Поступательное движение — это двние, при котором любая прямая, жестко
связанная с движущимся телом,
остается параллельной своему
первоначальному положению и все
точки тела совершают одинаковые
перемещения.
Вращательное движение — это
дв-ние, при котором все точки
тела движутся по окружностям,
центры которых лежат на одной
и той же прямой, называемой
осью вращения.
Угловая скорость

27.

перемещение
некоторой
точки М твердого тела
М’
первая
производная
dr
dt
вторая производная
не могут служить
характеристикой движения
всего твердого тела.
понятие вращательного движения
для материальной точки
неприемлемо
2
dr
dt
2

28.

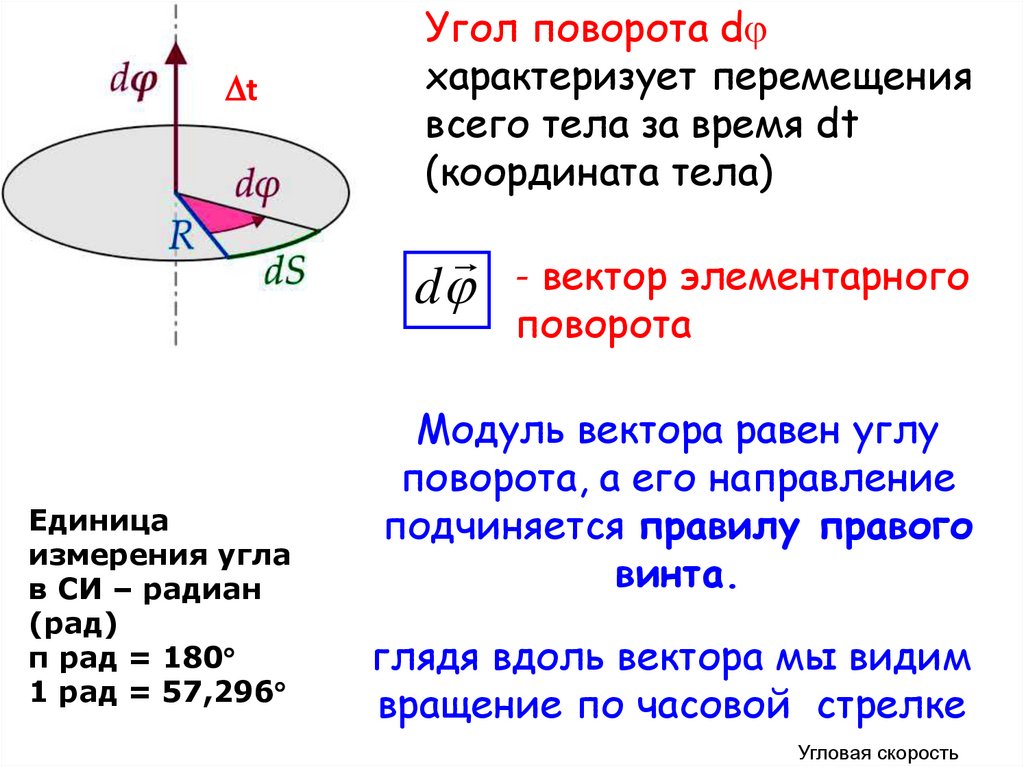
t
Угол поворота d
характеризует перемещения
всего тела за время dt
(координата тела)
d
Единица
измерения угла
в СИ – радиан
(рад)
π рад = 180
1 рад = 57,296
- вектор элементарного
поворота
Модуль вектора равен углу
поворота, а его направление
подчиняется правилу правого
винта.
глядя вдоль вектора мы видим
вращение по часовой стрелке
Угловая скорость

29.

=const для всех
точек тела
Угловой скоростью наз-ся
вектор
численно
равный
первой производной от угла
поворота по времени и
направленный
вдоль
оси
вращения в направлении
d
lim
t 0 t
dt
,
Направления всегда
совпадают
d
Единица угловой
скорости — радиан
в секунду (рад/с).
Линейная скорость

30.

dS Rd
dS dt
dS Rd
υ
ωR
dt
dt
Линейная скорость точки
В векторной форме
R Sin ( R)
υ [ω, R ]
R
Вектор ортогонален к векторам
и
и направлен в ту же сторону, что и векторное
произведение
[ω, R ]
совпадает с направлением поступательного движения
правого винт а при его вращении от ωПериод
к R.вращения

31.

const
if
Период Т – промежуток времени, в течение
которого тело совершает полный оборот (т.е.
поворот на угол 2 )
t
2π
T
2π
Т
ω
Частота вращения – число полных оборотов,
совершаемых телом при равномерном его
движении по окружности в единицу времени:
1
1
T 2
2
2
Угловое ускорение

32.

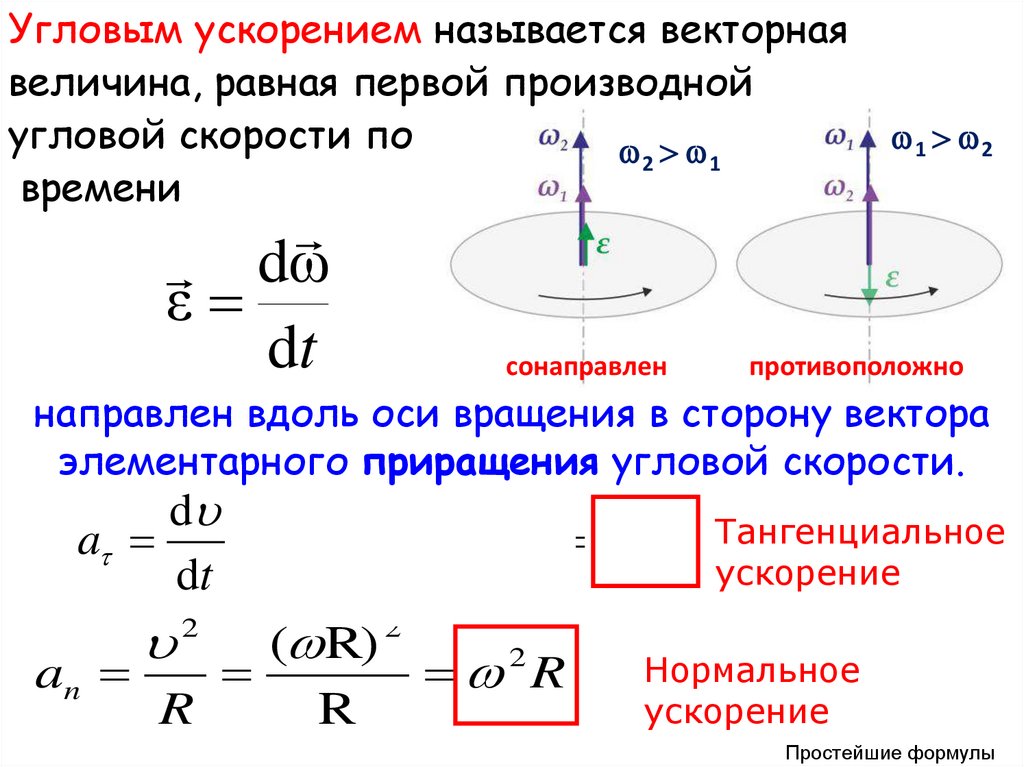
Угловым ускорением называется векторная
величина, равная первой производной
угловой скорости по
2 1
времени
dω
ε
dt
сонаправлен
1 2
противоположно
направлен вдоль оси вращения в сторону вектора
элементарного приращения угловой скорости.
d d
d
a
( R) R
R Тангенциальное
ускорение
dt dt
dt
2
2
( R)
Нормальное
an
2R
ускорение
R
R
Простейшие формулы

33.

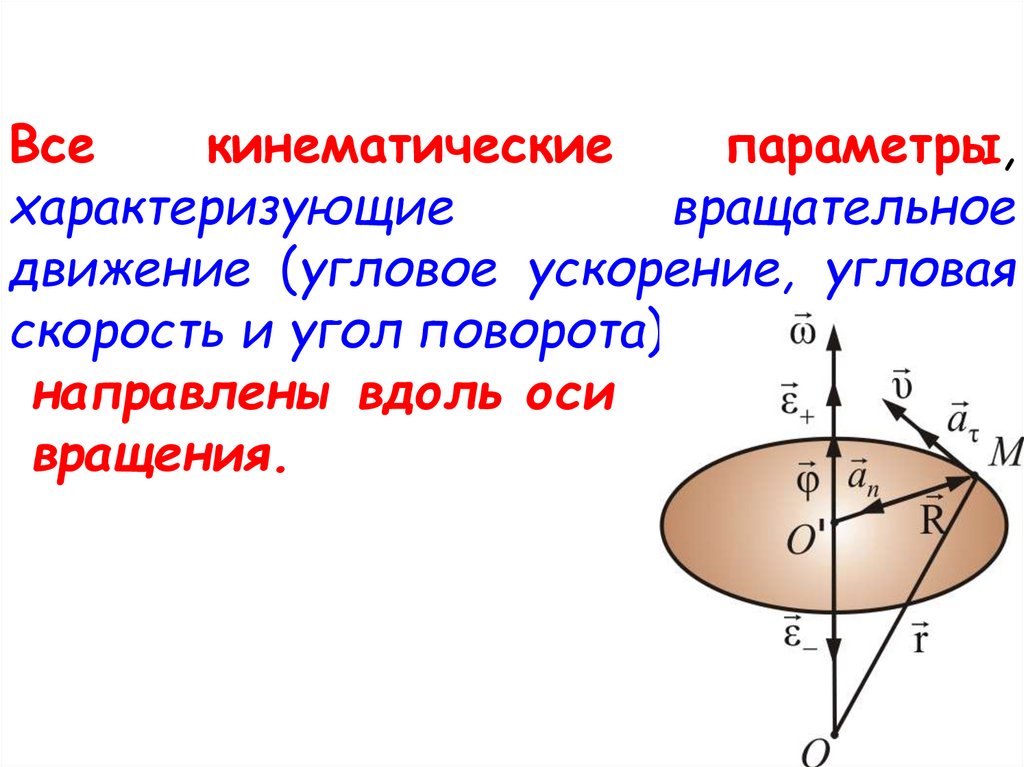
Все
кинематические
параметры,
характеризующие
вращательное
движение (угловое ускорение, угловая
скорость и угол поворота)
направлены вдоль оси
вращения.

34.

Формулы простейших случаев вращения тела
вокруг неподвижной оси:
- равномерное вращение
ε 0; ω const;
t;
- равнопеременное
ε const ;
вращение
ω ω 0 εt
εt
φ ω 0t
2
2

35.

Тест 2.
Сравнить нормальное
ускорение точек на
поверхности земного шара?
an R
2
А. на экваторе
R =max
1) наибольшее
Б. на широте 60˚
R =R cos
2)наименьшее
В. на полюсах
R =min
3)среднее

36.

Соответствие линейных и угловых
величин
Линейные
Угловые
x, y, z - координаты
- угол поворота
радиус-вектор
r
скорость
v
-угол поворота
a
S = R
-ускорение
v = R
- угловая скорость
- угловое ускорение
a = R
an = 2R

37.

Тангенциальн Нормальное Движение
a = 0
a n= 0
Прямолинейное
равномерное движение
a = const
a n= 0
Прямолинейное
равнопеременное движение
a = f(t)
a n= 0
Прямолинейное движение с
переменным ускорением
a = 0
a n = const
Равномерное движение по
окружности
a = 0
a n 0
Равномерное
криволинейное движение
a = const
a n 0
Криволинейное
равнопеременное движение
a = f(t)
a n 0
Криволинейное движение с
переменным ускорением
Вращательное движение

38.

1.(а + b)2 = a2 + b2
2.
1
1 1
a b a b
Х
.Х
3. Половина от 10-10
равна 10-5.
4.
5.
6.
1
4 : 2.
2
Х
Х
16ab 4ab.
a x a x
b y b y
8. 10-10/10-5= 10-15. Х
9. logAB = logA·logB.
Х
10. sin(A+B)= sinA +
sinB. Х
Х
Х
7. ½ от 10-8 равна 5-8.
Х