Похожие презентации:
Алгоритм решения линейных уравнений
1.
1. Алгоритм решениялинейных уравнений
2.
• 1. Привести к стандартному виду: ax b 0• 2. Слагаемые с переменной оставить в
левой части, без переменной перенести в
правую часть уравнения, изменив знак на
противоположный: ax в
• 3. Разделить обе части уравнения на
коэффициент при переменной: ax в :a
b
• 4. Найти значение переменной
x
a
• 5. Записать ответ.
3.
Примеры1)6 x 12 0
6 x 12
x 12 : 6
x 2
Ответ : 2
2)8 4 x 8
4 x 8 8
4 x 16
x 16 : ( 4)
x 4
Ответ : 4
4.
Алгоритм решения квадратныхуравнений
1. Привести к стандартному виду: ах 2 вх с 0
2. Найти дискриминант по формуле: Д в 2 4ас
в Д
ЕслиД 0, то _ уравнение _ имеет _ 2корня : х
2а
в
ЕслиД 0, то _ уравнение _ имеет _ один _ корень : х
2а
ЕслиД 0, то _ уравнение _ корней _ не _ имеет
3. Записать ответ.
5.
Алгоритм решения линейных неравенств1.Привести к стандартному виду: ax b 0
Или ax b 0
2. Слагаемые с переменной оставить в левой части,
без переменной перенести в правую часть уравнения,
изменив знак на противоположный: ax в
ax в
3. Разделить обе части уравнения на коэффициент
при переменной: ax в :а
ax в : а
4. Записать ответ в виде интервала.
При делении на отрицательное число- знак
неравенства меняется на противоположный
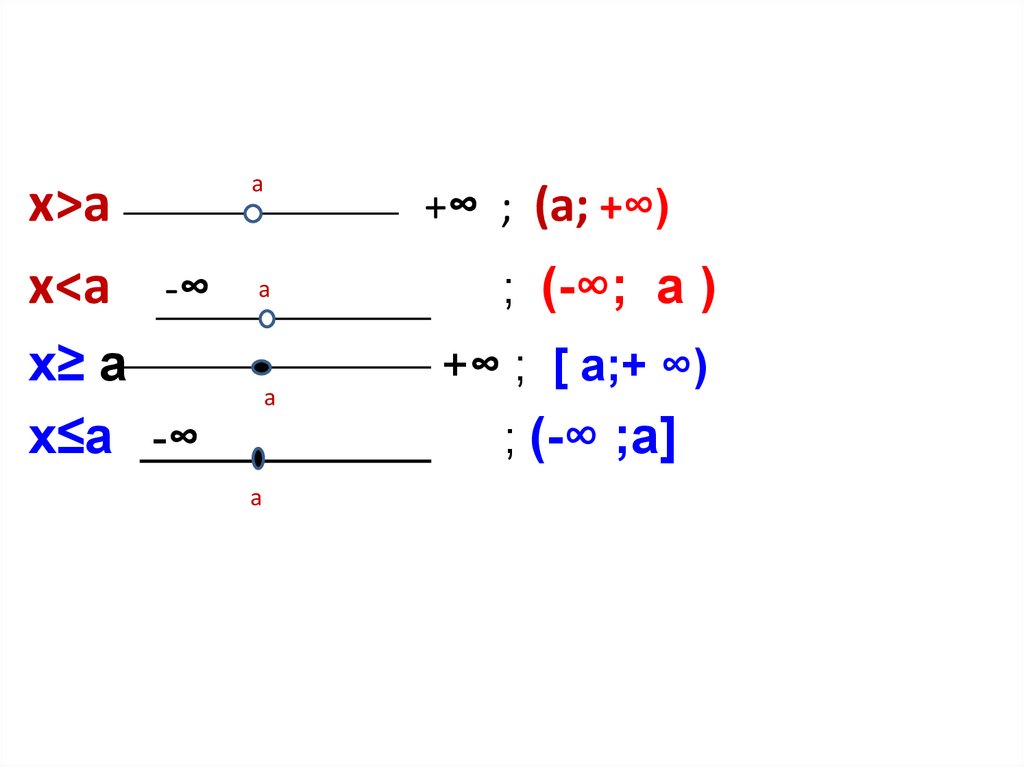
6.
х>ах<а -∞
а
а
х≥ а
х≤а -∞
а
а
+∞ ; (а; +∞)
; (-∞; а )
+∞ ; [ а;+ ∞)
; (-∞ ;а]
7.
Примеры1)3 х 2 13
3 x 13 2
3 x 15
x 5
Ответ : (5 : )
2)35 2 х 1
2 х 1 35
2 х 34 : ( 2) Знак _ неравенства
х 17
изменится _ на _ противоположный
Ответ : [17; )
8.
Алгоритм решения квадратныхнеравенств 2
1. Привести к стандартному виду:
ах вх с 0
2
ax
bx c 0
2
2. Приравнять к нулю левую часть: ах вх с 0
3. Найти корни, получившегося уравнения.
4. Отметить корни на числовой прямой, разбив ее на
интервалы.
5. Определить знак функции в каждом интервале(если
коэффициент а>0, то в последнем интервале знак «+»)
6. Выбрать интервал в соответствии со знаком
неравенства.
Знак > или ≥ - интервал со знаком «+»
Знак < или ≤ - интервал со знаком «-»
9.
Примеры1) x 2 x 24 0
2
x 2 x 24 0
2
x1 4; x 2 6
+
-6
Ответ : ( ; 6)и (4; )
-
4
+
10.
х х 12 02
х
2
х 12 0
х1 4
х2 3
Ответ : [ 3;4]
3
4
11.
2х 33)
0 _ Перейдем _ к
5 2х
равносильному _ неравенству :
(2 x 3)(5 2 x) 0
2 x 3 0; _ 5 2 x 0
x 1,5 ___ x 2,5
1,5
Ответ : ( ; 1,5)и (2,5; )
2,5








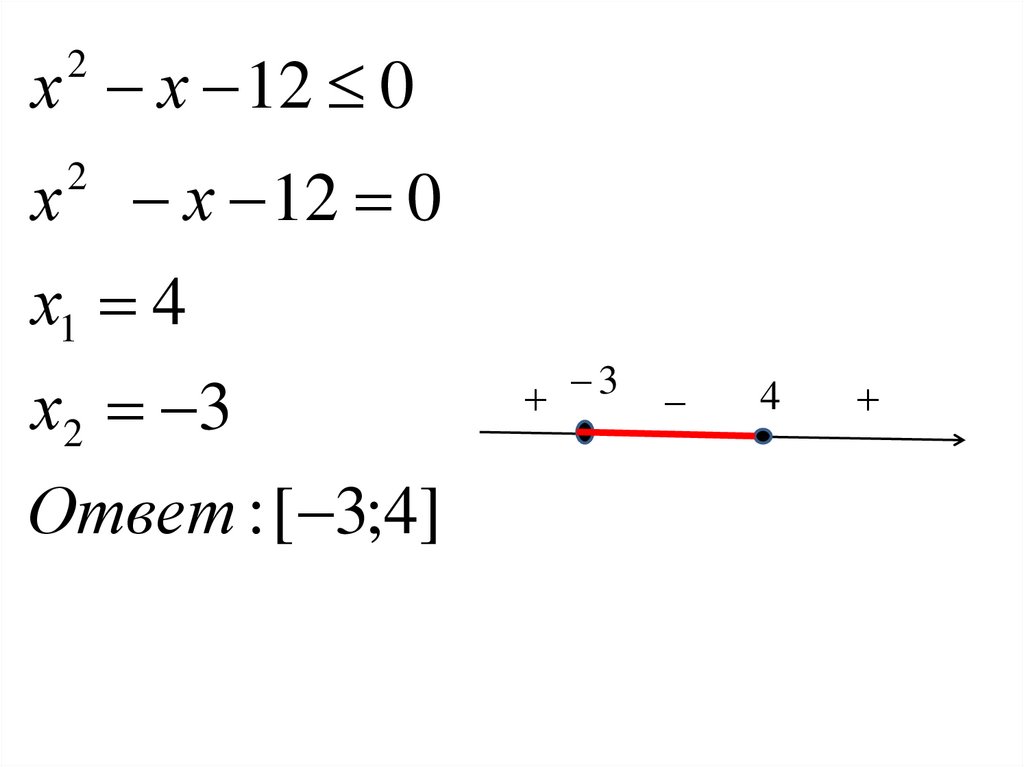

 Математика
Математика








