Похожие презентации:
Дифференциальное исчисление функций нескольких переменных
1. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Модуль 52. § 1. Понятие функции двух переменных.
§ 1. Понятие функции двухпеременных.
3.
• Пусть x, y – две независимыедруг от друга переменные.
Графически пару независимых
переменных (x, y) можно
представить как точку M(x, y) на
плоскости xOy. Пусть D –
некоторое множество точек
M(x, y).
4.
• Опр. Если каждой точке M(x, y)из множества D по некоторому
закону f ставится в соответствие вполне определенное
действительное число z, то
говорят, что z есть функция двух
переменных x и y и пишут
z = f(x, y) или z = f(M),
где M = M(x, y) – точка плоскости.
5.
• Геометрическим изображениемфункции двух переменных
является некоторая поверхность
в трехмерном пространстве.
6. Примеры:
• График функции2
z x y
2
• (эллиптический параболоид)
7.
• график функцииz x y
2
2
(гиперболический параболоид)
8.
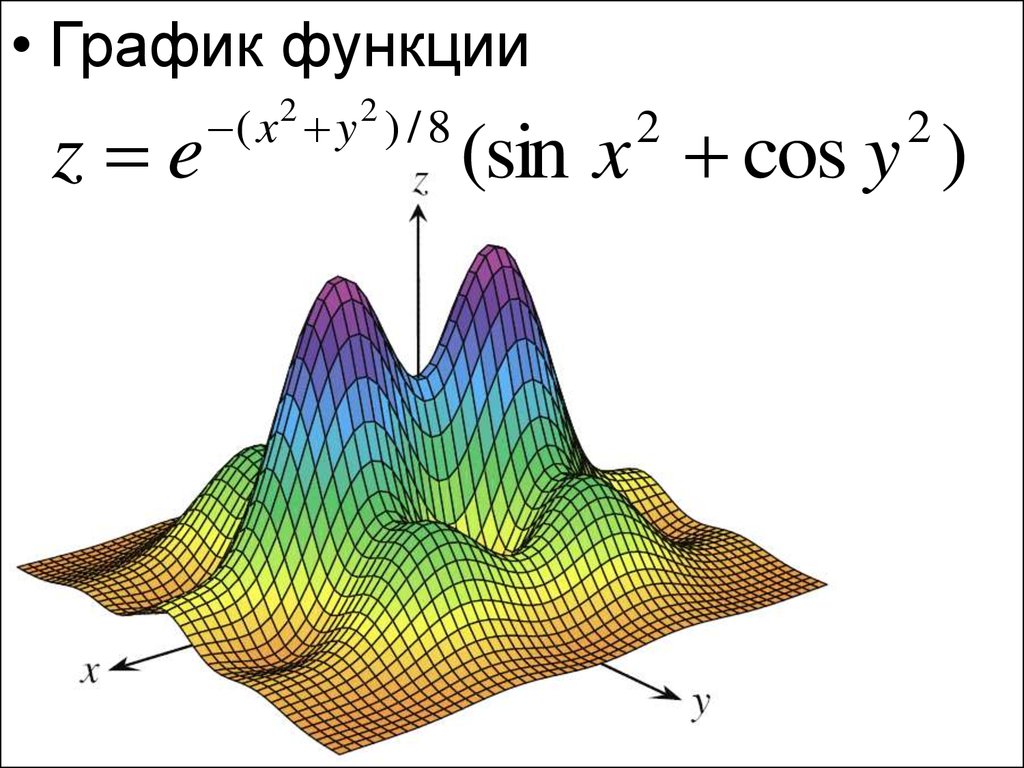
• График функцииz e
( x 2 y 2 ) / 8
(sin x cos y )
2
2
9.
• График функции z sin x 2 sin y10.
• Опр. Областью определенияфункции z = f(x, y) называется
множество D точек M(x, y), в
которых функция z = f(x, y)
определена и может быть
вычислена. Все значения,
которые принимает функция
z = f(x, y) (в области ее
определения), образуют
множество значений функции.
11. Примеры
12. Графическое изображение области определения функции.
• Пример. Построим областьопределения функции
w
y x
2
13.
14. Линии уровня
• Опр. Множество точекплоскости таких, что функция
f(x, y) принимает в них одно и то
же значение, f(x, y) = c,
называется линией уровня.
15.
16.
17.
18.
19. Построение графика функции двух переменных
• Рассмотрим пример построенияграфика функции
f ( x, y) 100 x y
2
2
20.
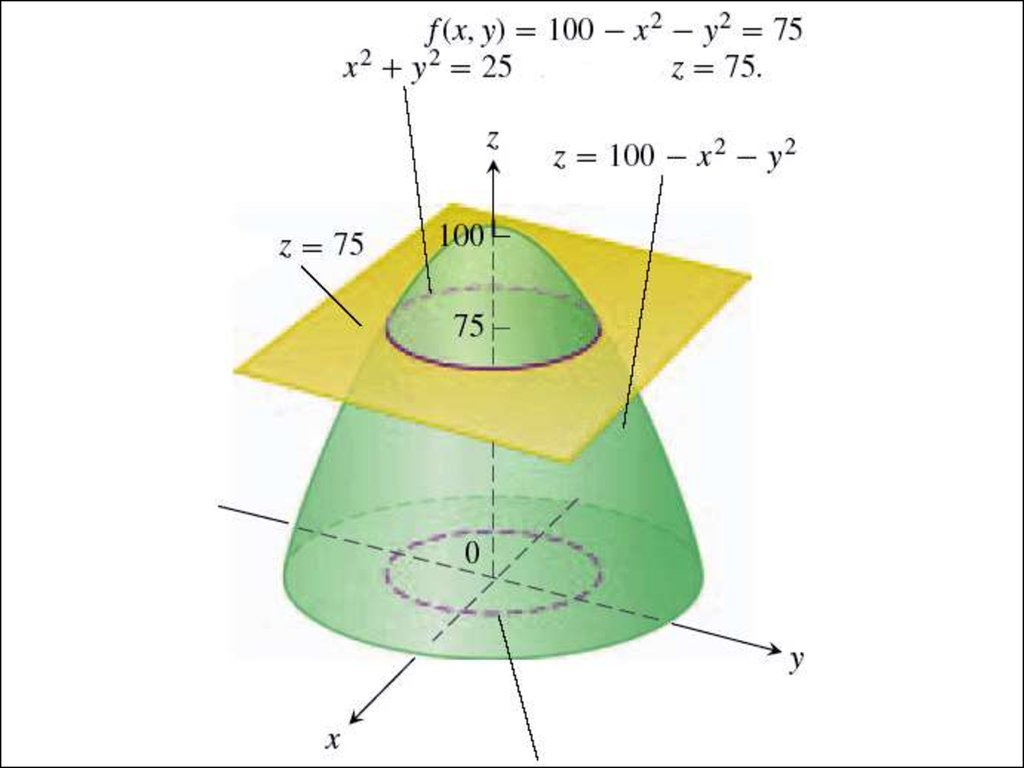
• Зафиксируем какое-нибудьзначение этой функции,
например, z = 75. Тем самым мы
определили в пространстве
плоскость z = 75. Находим
линию уровня при z = 75:
• 100 – x2 – y2 = 75, откуда
x2 + y2 = 25 – уравнение
окружности.
21.
22.
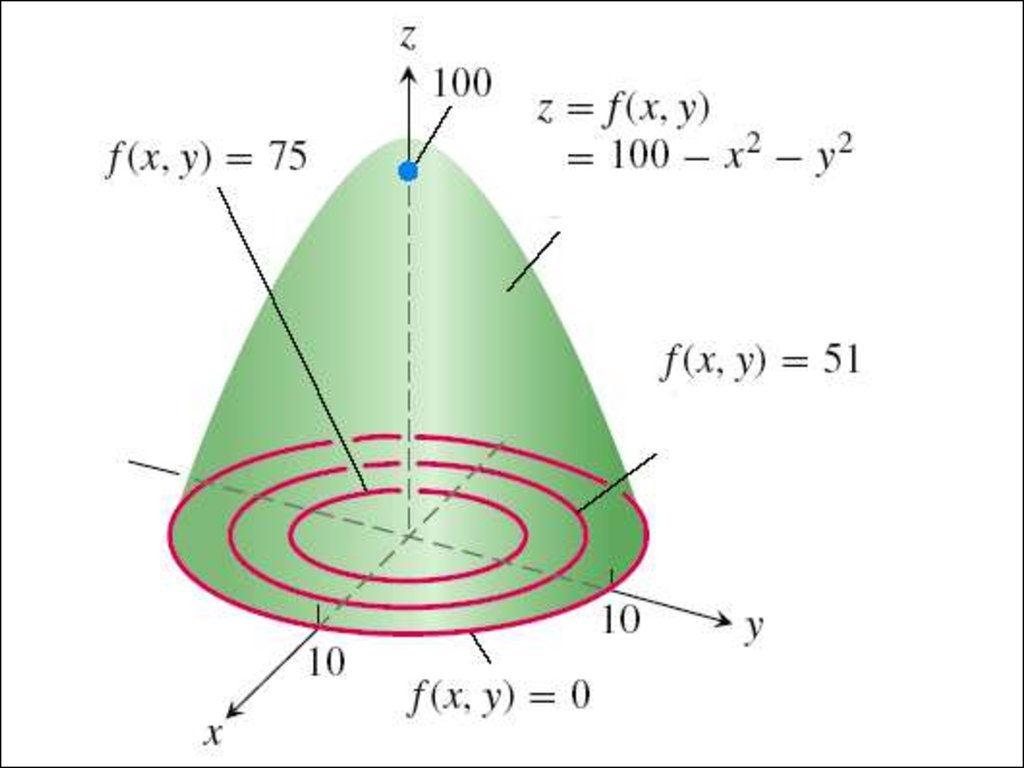
• Находя множество линийуровня, строим весь график.
23.
24. § 2. Понятие функции трех и более переменных.
§ 2. Понятие функции трех иболее переменных.
• Всякая упорядоченная
совокупность действительных
чисел (x1, x2, …, xn) называется
точкой n–мерного пространства
Rn. Пусть D – некоторое множество точек пространства Rn.
25.
• Опр. Если каждой точкеM(x1, x2, …, xn) из области D по
некоторому закону f ставится в
сответствие вполне
определенное число u, то
говорят, что u есть функция n
переменных и пишут
u = f(x1, x2, …, xn) или u = f(M)
где M = M(x1, x2, …, xn) – точка
n–мерного пространства.
26. Примеры
27.
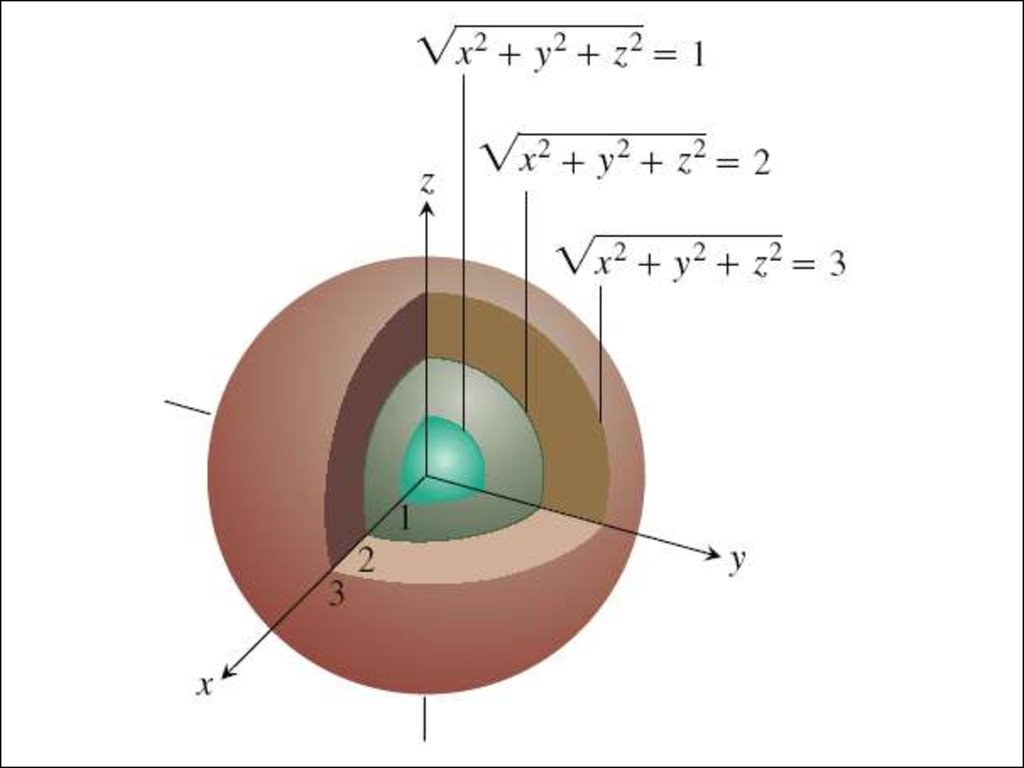
• Опр. Множество точекпространства, в которых
функция трех переменных
f(x, y, z) принимает одно и то же
значение, f(x, y, z) = c,
называется поверхностью
уровня.
28.
29. § 3. Предел и непрерывность функции нескольких переменных
§ 3. Предел и непрерывностьфункции нескольких
переменных
30.
• Опр. Число A называетсяпределом функции z = f(x, y) в
точке M0(x0, y0), если для
каждого числа ε > 0 найдется
такое число δ = δ(ε), что при
0 < |x – x0| < δ и 0 < |y – y0| < δ
выполняется неравенство
|f(x,y) – A| < ε. При этом пишут
A lim f ( x, y) lim f (M )
x x0
y y0
M M 0
31.
• Опр. Функция z = f(x, y)называется непрерывной в
точке M0(x0, y0), если функция
z = f(x, y) определена в этой
точке и существует
lim f ( x, y) f ( x0 , y0 ).
x x0
y y0
32.
• Аналогичные определенияимеют место и для функции
u = f(x1, x2, …, xn) в случае
произвольного числа n
переменных.
33.
• Если в какой – либо точкеусловие непрерывности не
выполняется, то эта точка
называется точкой разрыва
функции f(x, y). Это может быть
в следующих случаях:
34.
• 1. Функция z = f(x, y) неопределена в точке M0(x0, y0).
• 2. Не существует предел
lim f ( x, y)
x x0
y y0
• 3. Этот предел существует, но он
не равен f(x0, y0).
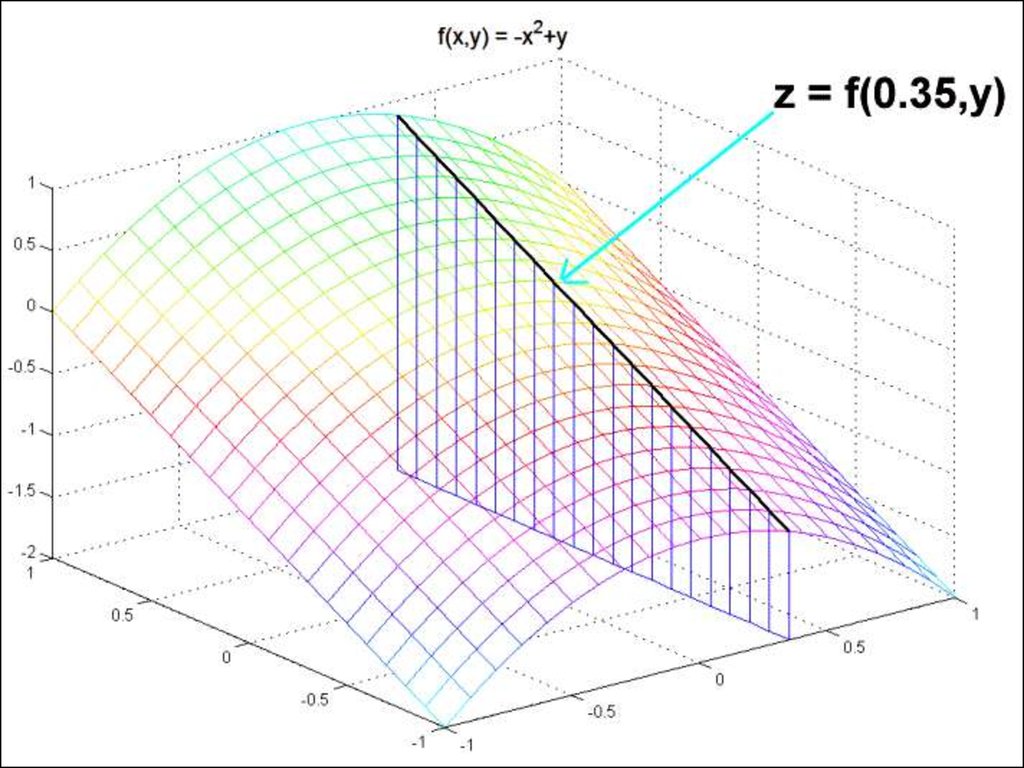
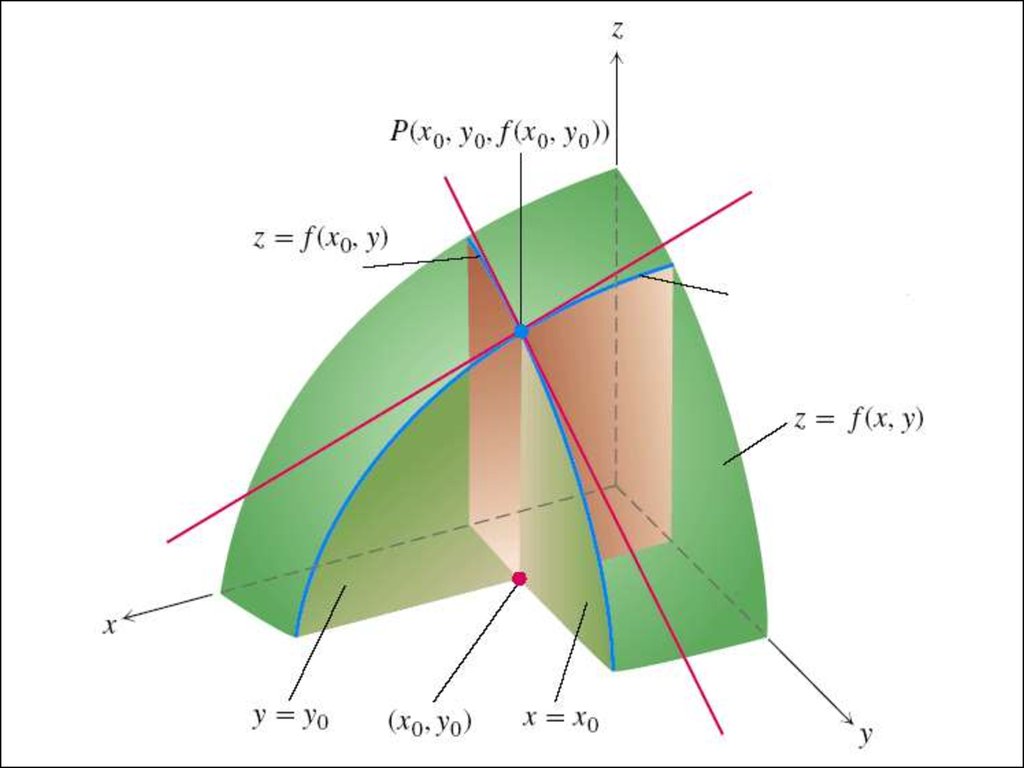
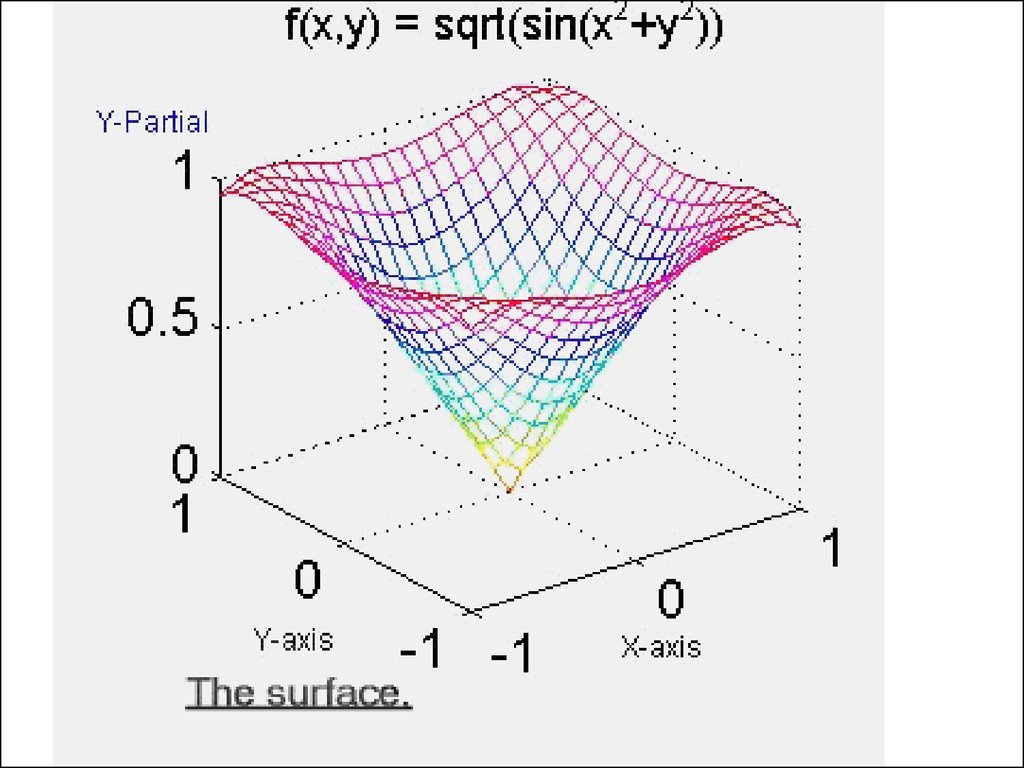
35. § 4. Частные производные функции нескольких переменных
§ 4. Частные производныефункции нескольких
переменных
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
• Пусть z = f(x, y) – функция двухпеременных. Дадим
независимой переменной x
приращение Δx, оставляя при
этом переменную y неизменной.
Тогда функция z получит
приращение
x z f ( x x, y ) f ( x, y )
которое называется частным
приращением z по x.
46.
• Аналогично, если независимойпеременной y дадим
приращение Δy, оставляя при
этом неизменной переменную x,
то функция z получит
приращение
y z f ( x, y y) f ( x, y),
называемое частным
приращением z по y.
47.
• Опр. Частной производной по xот функции z называется
предел отношения частного
приращения Δxz к приращению
Δx при стремлении Δx к нулю.
• Эта производная обозначается
одним из символов
z
, z x ,
x
f
,
x
f x ( x, y ).
48.
Таким образом, по определению,xz
f ( x x, y) f ( x, y)
z
lim
lim
x x 0 x x 0
x
49.
• Аналогично определяетсячастная производная от функции z = f(x, y) по переменной y :
yz
f ( x, y y ) f ( x, y )
z
lim
lim
y y 0 y y 0
y
Обозначается одним из символов
z
f
, z y ,
,
y
y
f y ( x, y).
50.
• В общем случае частнойпроизводной первого порядка
функции u = f(x1, x2, …, xn) по
переменной xk называется
предел
xk u
u
lim
xk xk 0 xk
f ( x1 , , xk xk , , xn ) f ( x1 , , xk , , xn )
lim
xk 0
xk
51.
• Т.к. при вычислении частныхпроизводных все переменные,
кроме одной, считают
постоянными, то для частных
производных сохранаяются все
правила и формулы
дифференцирования функции
одной переменной.
52.
• Пример. Найти частныепроизводные функции
x
z x y
y
2
53.
• Решение. Полагая y = const,находим
z
1
2 xy
x
y
54.
• Полагая x = const, находимz
1
x
2
2
x 1 x( 2 ) x 2
y
y
y
55.
• Пример. Найти значениячастных производных функции
2
2
u ln( x y ) xyz
в точке M(1, –1, 0).
56.
• Решение. Полагая y = const,z = const, находим
u
1
2
(
2
x
0
)
1
yz
2
y
,
z
c
x
x y
2x
2
yz
2
x y
Ì
2
0 1
1 1
57.
• Аналогично находимu
1
2
(
0
2
y
)
1
xz
2
x
,
z
c
y
x y
2y
2
2
xz
0
1
2
x y
1 1
M
u
0 1 xy xy M 1
z x, y c
58.
• Предположим, что функцияz = f(x, y) имеет непрерывные
частные производные
z
f x ( x, y )
x
z
f y ( x, y)
y
59.
• Эти производные в своюочередь являются функциями
независимых переменных x и y.
Будем называть f x ( x, y )
f y ( x, y ) частными
и
производными 1-го порядка.
60.
• Частными производными 2-гопорядка называются частные
производные от частных
производных 1-го порядка.
• Для функции z = f(x, y) двух
переменных можно найти
четыре частные производные 2го порядка, которые обозначаются следующим обр-м:
61.
62.
• В общем случае смешанныечастные производные могут не
совпадать, однако для них
справедлива теорема:
• Теорема. Если смешанные
частные производные f xy и f yx
непрерывны в некоторой точке
M(x, y), то они равны, т. е.
f xy ( x, y) f yx ( x, y)
63.
• Частными производными n–гопорядка называются частные
производные от частных
производных (n – 1)–го порядка.
• Их обозначают
z
,
n
x
n
и т. д.
z
,
n 1
x y
n
z
n 2
2
x y
n
64.
• Частные производные любогопорядка, взятые по различным
переменным, называются
смешанными.
65.
• Пример. Найти частныепроизводные 2-го порядка
функции
3 2
z x y sin( xy 1)
66.
• Решение. Последовательнонаходим
z
2 2
3x y y cos(xy 1);
x y c
z
3
2 x y x cos(xy 1);
y x c
67.
z2 2
3
x
y
y
cos(
xy
1
)
2
y c
x
x
2
2
6 xy y sin( xy 1);
2
y c
z
2 2
3x y y cos( xy 1)
x c
x y y
2
6 x y cos( xy 1) yx sin( xy 1);
2
x c
68.
z3
2 x y x cos( xy 1
y c
y x x
2
6 x y cos( xy 1) yx sin( xy 1)
2
y c
z
3
2
x
y
x
cos(
xy
1
)
2
x c
y
y
2
2 x x sin( xy 1)
3
x c
2

















































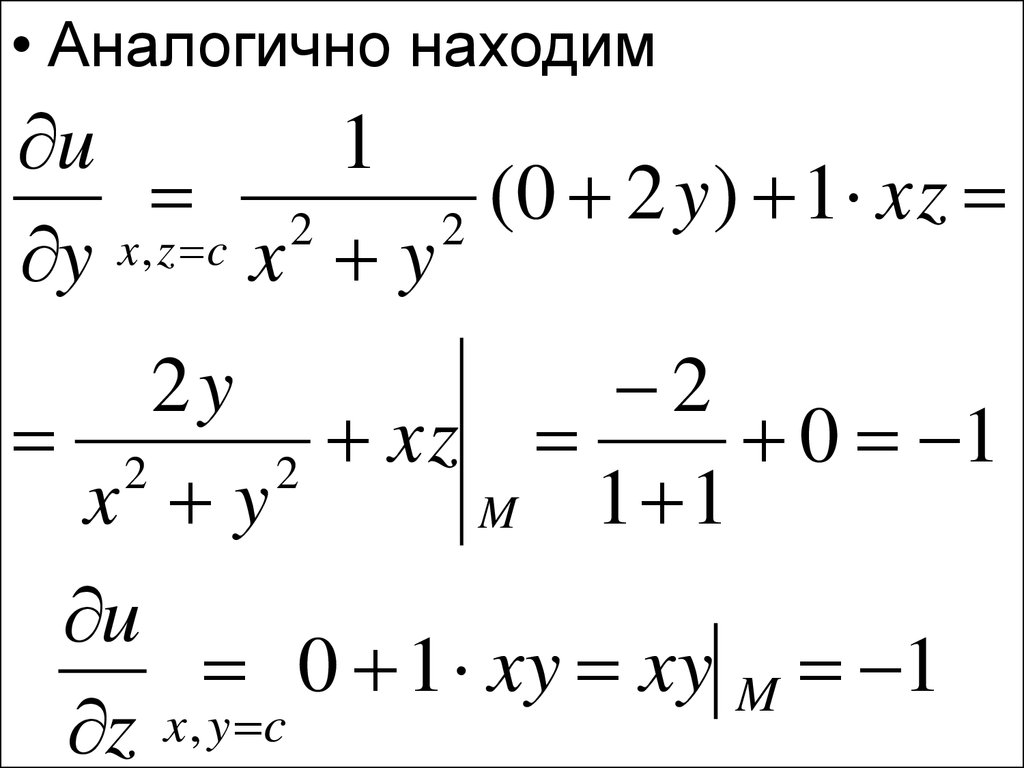









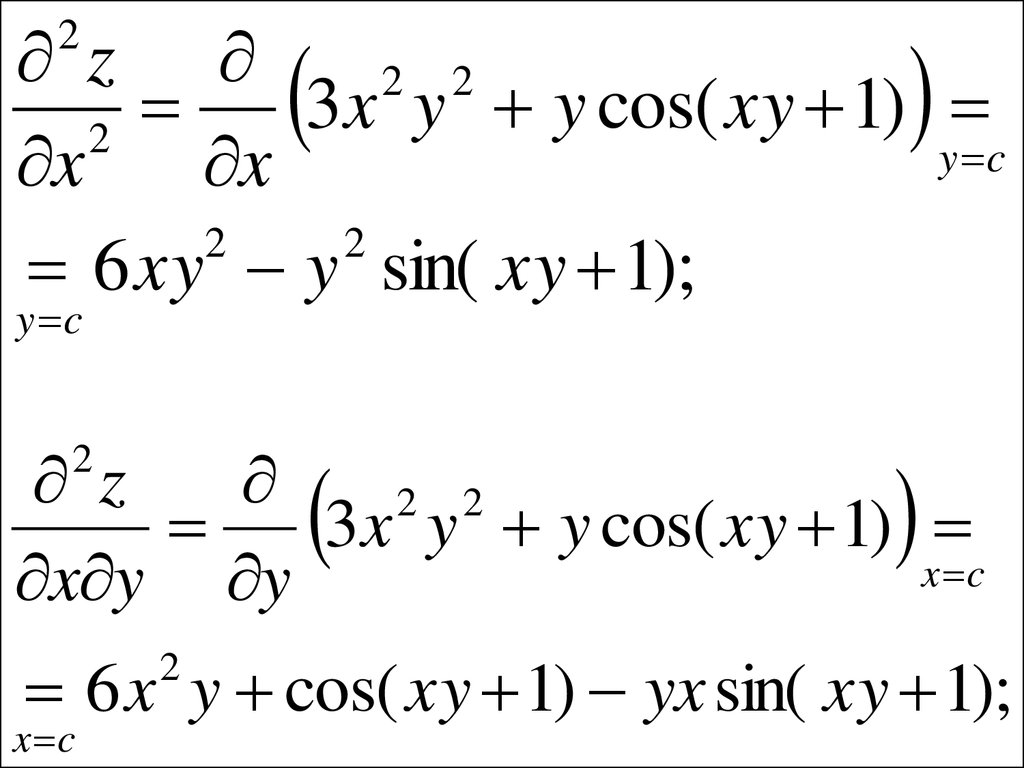




 Математика
Математика








